The Birthday Paradox - Irish translation (original) (raw)
Original article: http://www.efgh.com/math/birthday.htm
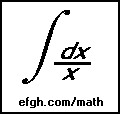 |
An Paradox Breithlá Philip J. Erdelsky 4 Iúil, 2001 |
|---|
Is é an fhadhb is fearr leat i gcúrsaí dóchúlachta agus staitisticí tosaigh ná an Fadhb Breithlá: Cad é an dóchúlacht go bhfuil an bhreithlá céanna ar a laghad dhá duine N a roghnaíodh go randamach? (An mhí céanna agus an lá céanna, ach ní gá an bhliain chéanna.)
An dara cuid den fhadhb:Cé chomh mór is gá N a bheith ionas go mbeidh an dóchúlacht níos mó ná 50 faoin gcéad? Is é 23 an freagra, rud a bhuaileann an chuid is mó daoine go míréasúnach beag. Ar an gcúis seo, is minic a dtugtar an BreithiúnasParadox ar an bhfadhb. Molann roinnt gealltaí gealltóireachta,ar airgead fiú, go bhfuil lá breithe dúbailte i measc aon ghrúpade 23 duine nó níos mó. Is dócha go bhfuil roinnt suiceanna neamhfhiosacha anna ghlacfaidh leis an geall.
Déantar an fhadhb a shimpliú de ghnáth trí dhá rud a ghlacadh:
Níor rugadh aon duine ar 29 Feabhra.
Déantar dáileadh breithe an phobaila dháileadh go cothrom thar an 365 lá eile den bhliain eile.
Ceann de na chéad rudaí le fógra faoin fhadhb seo ná go bhfuil sé i bhfad níos éasca an fhadhb comhlántach a réiteach: Cad é an dóchúlacht go bhfuil gach lá breithe difriúil ag daoine roghnaithego randamach? Is féidir linn seo a scríobh mar fheidhm athchúrsach:
double_birthdays (int n)
{
tuairisceán n == 1? 1.0: different_birthdays (n-1) * (365.0- (n-1)) / 365.0;
}
Ar ndóigh, le haghaidh N = 1 is é an dóchúlacht1. I gcás N> 1, is é an dóchúlacht go bhfuil dhá thionchar ann:
Gobhfuil gach lá breithe difriúla agan gcéad duine N-1.
Gobhfuil difríocht lá breithe ag an duineó aon cheann den chéad N-1.
Téann clár chun na dóchúlachtaí a thaispeáintmar seo:
Príomhní neamhní (neamhní)
{
int n;
le haghaidh (n = 1; n <= 365; n ++)
printf ("% 3d:% e \ n", n, 1.0-different_birthdays (n));
}
Is é an toradh atá mar seo:
1: 0.000000e + 00
2: 2.739726e-03
3: 8.204166e-03
4: 1.635591e-02
5: 2.713557e-02
20: 4.114384e-01
21: 4.436883e-01
22: 4.756953e-01
23: 5.072972e-01
24: 5.383443e-01
25: 5.686997e-01
An dóchúlacht go bhfuil arduithe lá breithe os cionn0.5 duine ar a laghad de dhaoine N nuair a bhíonn N = 23.
MÓ CAD FAOI BHLIAIN LEAP BLIAIN?
Is féidir an fhadhb bhunaidh a réiteach le riail sleamhnáin, rud a rinne mégo díreach nuair a chuala mé go leor é, blianta fada ó shin.
Má chuireann muid 29 Feabhra leis an meascán, faigheann sé i bhfad níos casta. Sa chás seo, déanfaimid roinnt boinn tuisceana breise:
Rugtar líon comhionann daoine ar laethanta seachas 29 Feabhra.
Is é an líon daoine a rugadh ar 29 Feabhra ná ceathrú cuid den líon daoine a rugadh ar aon lá eile.
Dá réir sin is é 0.25 / 365.25 an dóchúlacht gur rugadh duine roghnaithego randamach ar 29 Feabhra agus is é an dóchúlacht gur rugadh duine roghnaithego randamach ar lá sonraithe amháin ná 1 / 365.25.
Is é an dóchúlachtgo n-éireoidh le daoineN, a d'fhéadfadh a bheith ar cheann acu a rugadh ar29 Feabhra, laethanta breithe difriúla dhá dóchúlacht:
Go n-rugadh na daoine N ar N lá éagsúla seachas 29 Feabhra.
Rugadh na daoineN ar lá éagsúla N, agus duine amháin a rugadh ar 29 Feabhrasan áireamh.
Cuireann na dóchúlachtaíleis mar go bhfuil an dá chás eisiach.
Anois is féidir gach dóchúlacht a churin iúl go cúrsach:
dúbailte different_birthdays_excluding_Feb_29 (int n)
{
tuairisceán n == 1? 365.0 / 365.25:
different_birthdays_excluding_Feb_29 (n-1) * (365.0- (n-1)) / 365.25;
}
dúbailte different_birthdays_including_Feb_29 (int n)
{
tuairisceán n == 1? 0.25 / 365.25:
different_birthdays_including_Feb_29 (n-1) * (365.0- (n-2)) / 365.25 +
different_birthdays_excluding_Feb_29 (n-1) * 0.25 / 365.25;
}
Téann clár chun na dóchúlachtaí a thaispeáintmar seo:
Príomhní neamhní (neamhní)
{
int n;
le haghaidh (n = 1; n <= 366; n ++)
printf ("% 3d:% e \ n", n, 1.0-different_birthdays_excluding_Feb_29 (n) -
different_birthdays_including_Feb_29 (n));
}
Is é an toradh atá mar seo:
1: -8.348357e-18
2: 2.736445e-03
3: 8.194354e-03
4: 1.633640e-02
5: 2.710333e-02
20: 4.110536e-01
21: 4.432853e-01
22: 4.752764e-01
23: 5.068650e-01
24: 5.379013e-01
25: 5.682487e-01
De réir mar a bhíothas ag súil leis, tá na dóchúlachtaí beagán níos ísle, toisc go bhfuil dóchúlacht níos ísle ann le comóntaí lá breithe nuair a bhíonn breitheanna breithe ann. Ach is é an líon is lúle dóchúlacht níos mó ná 0.5 fós 23.
Ar ndóigh, féadfaidhpurist matamaitice a mhaíomh nach dtéann blianta léim i gcónaí gach ceithre bliana,agus mar sin ní mór na modhanna a mhodhnú tuilleadh. Mar sin féin, baé an bhliain dhá bhliain déag a bhí ina bhliain leapach ná 1900, agus is é an chéad cheann eile ná 2100. Is é an líon daoine atá ina gcónaí anois a rugadh i 1900 chomh beagis dóigh liom go bhfuil ár gcomhfhogasú bailí chun críocha praiticiúla go léir. Ach tá fáilte roimh na modhnuithe riachtanacha a dhéanamh más mian leat.
Tá impleachtaí agan gCréithiúnas Breithlá thar shaol gealltóireachta na bparóige. Is é teicníocht chaighdeánach i stóráil sonraí gach uimhir a shannadh ar a dtugtar códhash. Ansin stóráiltear an ítim i mbosca a fhreagraíonn dá chód hash. Luasann sé seo ar aisghabháil mar ní mór ach aon bhosca amháin a chuardach. Taispeánann an BreithiúnasParadox go bhfuil an dóchúlachtgo mbeidh dhá ítim nó níos mó suas sa bhosca céanna ard fiú má tá líon na n-ítimí i bhfad níos lú ná líon na mboscaí. Mar sin, tá gá le láimhseáil éifeachtach na mboscaí ina bhfuil dhán-ítim nó níos mó i ngach cás.