確率密度関数とは 読書の人気・最新記事を集めました - はてな (original) (raw)
確率密度関数
(
読書
)
【
かくりつみつどかんすう
】
連続型確率分布における、確率を確率変数の関数として表したもの。
確率変数xに対してf(x)とあらわされる。
このタグの解説についてこの解説文は、すでに終了したサービス「はてなキーワード」内で有志のユーザーが作成・編集した内容に基づいています。その正確性や網羅性をはてなが保証するものではありません。問題のある記述を発見した場合には、お問い合わせフォームよりご連絡ください。
関連ブログ

Kevin's Data Analytics Blog•3年前
確率分布の期待値・分散・母関数まとめ~連続分布~ 以前の記事に続き、統計検定1級/準1級の対策として、各確率分布の期待値・分散・母関数について整理しました。 今回は、連続分布を扱いました。 離散分布のまとめについてはこちらを参照ください。 確率分布の期待値・分散・母関数まとめ~離散分布~ - Kevin's Data Analytics Blog 1. 連続一様分布 定義 𝑎確率密度関数の値が常に一定であるような確率分布を連続一様分布という。 確率密度関数 期待値 分散 積率母関数(モーメント母関数) 2. 正規分布 定義 𝜇∈"ℝ, " σ>0とし、確率変数𝑋に対して、以下の確率密度関数をもつ分布を正規分布という。𝜇を中心する左右対称の釣鐘…
以前の記事に続き、統計検定1級/準1級の対策として、各確率分布の期待値・分散・母関数について整理しました。 今回は、連続分布を扱いました。 離散分布のまとめについてはこちらを参照ください。 確率分布の期待値・分散・母関数まとめ~離散分布~ - Kevin's Data Analytics Blog 1. 連続一様分布 定義 𝑎確率密度関数の値が常に一定であるような確率分布を連続一様分布という。 確率密度関数 期待値 分散 積率母関数(モーメント母関数) 2. 正規分布 定義 𝜇∈"ℝ, " σ>0とし、確率変数𝑋に対して、以下の確率密度関数をもつ分布を正規分布という。𝜇を中心する左右対称の釣鐘…
#統計検定1級#統計検定準1級#確率分布#確率密度関数#積率母関数
ネットで話題
もっと見る
15ブックマーク確率密度関数の意味と具体例 | 高校数学の美しい物語
 manabitimes.jp
manabitimes.jp
10ブックマーク確率密度関数 - Wikipedia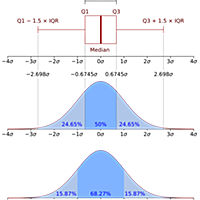
 ja.wikipedia.org
ja.wikipedia.org
10ブックマーク確率密度関数からモンテカルロ積分まで - Qiita
 qiita.com
qiita.com
8ブックマーク正規分布の確率密度関数の成り立ち |AVILEN正規分布の確率密度関数の式正規分布の確率密度関数は、次の式で表されます。 f(x)=12πσ2exp[−(x−μ)22σ2]f(x) = \frac{1}{\sqrt{2πσ^2}}\exp{[-\frac{(x-μ)^2}{2σ^2}]}f(x)=2πσ21exp[−2σ2(x−μ)2] 以下で、この式の導出過程を見ていきましょう。 確率密度関数の成り立ち確率密度関数の土台世の中の多くの事象は平均値... avilen.co.jp
avilen.co.jp
7ブックマーク確率, 確率分布関数, 確率密度関数まず例題を考えてみよう。 酔っぱらいが居酒屋から出て, 南から北に伸びる一本道をふらふら歩いている状況を考える。 この酔っぱらいはとりあえず北に向かおうとしているが, 完全に酒が足に来ていて, 前に進むか後に戻るかがぜんぜん予想できないものとする。 また, 彼あるいは彼女は最大時速kmの速さで歩くことができる... dsl4.eee.u-ryukyu.ac.jp
dsl4.eee.u-ryukyu.ac.jp
6ブックマーク多変量正規分布の確率密度関数の解説 | 高校数学の美しい物語
 manabitimes.jp
manabitimes.jp
5ブックマークmatplotlibで混合ガウス分布の確率密度関数をプロットする - Wolfeyes Bioinformatics betaPythonとNumpy/Scipyの練習.前回はNumpyを使って混合ガウス分布のEMアルゴリズムを実装で混合ガウス分布について取り扱ったので,今回は混合ガウス分布についての数式をおさらいしつつ,確率密度関数をプロットしようと思う. 混合ガウス分布の概要 混合ガウス分布は,複数のガウス分布の線形結合で表すことができる. ... yagays.github.io
yagays.github.io
5ブックマーク第51回 確率の数学 確率密度関数 | gihyo.jp
 gihyo.jp
gihyo.jp
関連ブログ

いろいろつれづれ•4年前
〖追記①②あり〗正規分布の縦軸や標準正規分布の縦軸って何?そういえば~一時期気になってた~【備忘録】 ーーーーーーーー 主要内容 紹介書籍 正規分布や標準正規分布の縦軸 〖追記①:2021/9/1追記 〖追記②:2021/9/3追記 ーーーーーーーー 昔、統計検定2級に合格したんですが、だいぶ忘れてます。統計学入門的な内容から勉強し直してます。 正規分布や標準正規分布の図はおなじみの物だと思いますが、縦軸を省略しているものが多く、そういや縦軸を省略せずに表すとするとどんな表記になるんだろ?と思ってたことがあります。自分の備忘録として記載したいと思います。 表題について解決に導いてくれた3冊の書籍を紹介させていただきます。 ↓↓↓ 紹介書籍 紹介書籍①: 【リンク】⇒Amazon/通販/商品紹介…
ーーーーーーーー 主要内容 紹介書籍 正規分布や標準正規分布の縦軸 〖追記①:2021/9/1追記 〖追記②:2021/9/3追記 ーーーーーーーー 昔、統計検定2級に合格したんですが、だいぶ忘れてます。統計学入門的な内容から勉強し直してます。 正規分布や標準正規分布の図はおなじみの物だと思いますが、縦軸を省略しているものが多く、そういや縦軸を省略せずに表すとするとどんな表記になるんだろ?と思ってたことがあります。自分の備忘録として記載したいと思います。 表題について解決に導いてくれた3冊の書籍を紹介させていただきます。 ↓↓↓ 紹介書籍 紹介書籍①: 【リンク】⇒Amazon/通販/商品紹介…
#統計#統計学#統計学入門#正規分布#標準正規分布#確率密度関数#累積分布関数#分布関数

tomtom58’s blog•2日前
セミパラメトリック手法の1種GAM(一般化法モデル)の理論 はじめに 最近私は、因果推論と並んでセミパラメトリック手法にとても興味関心を持っています。解釈したい部分はパラメトリックに、それ以外の部分はノンパラメトリックにといううたい文句はとても興味をそそられますよね。パラメトリックに規定して解釈性を担保するというのは、現実の実務においても多々やりますが、それ以外の解釈性が不要な部分に関して複雑な表現を許すことによって、複雑な事象のパラメトリックに定義した(基本線形)の係数値が正しい値になり得るということも考えられます。というわけで、非常にセミパラメトリック手法に私は期待を持っているわけです。 最近、私はセミパラメトリック手法の一種であるGAM(一般化法…
はじめに 最近私は、因果推論と並んでセミパラメトリック手法にとても興味関心を持っています。解釈したい部分はパラメトリックに、それ以外の部分はノンパラメトリックにといううたい文句はとても興味をそそられますよね。パラメトリックに規定して解釈性を担保するというのは、現実の実務においても多々やりますが、それ以外の解釈性が不要な部分に関して複雑な表現を許すことによって、複雑な事象のパラメトリックに定義した(基本線形)の係数値が正しい値になり得るということも考えられます。というわけで、非常にセミパラメトリック手法に私は期待を持っているわけです。 最近、私はセミパラメトリック手法の一種であるGAM(一般化法…

INTP型のブログ•4日前
プログラマーが数学を勉強した結果 微積分までやった、理解度は低いけど定積分解けと言われたら初歩的なやつだったら解けるぐらいまで。 駆け足で3日ぐらいで期待値->分散->標準偏差->正規分布->確率密度関数->累積分布関数までやって、その中で積分が必要になったので微分->積分とやった感じ 駆け足だからこそだとは思うけど、一番思ったのは文字の意味がわからんという部分 σやμやE[X]、∫にdxといった文字がぞろぞろと数式では出てくるけれど、これは非常に数学っていう文化をひしひしと感じさせられた プログラマ的に言うと過度にワンラインなコードと言った感じで、アン・リーダブルと言えそう。 ただこの辺はデジタル空間っていう有限だけどそれを…
微積分までやった、理解度は低いけど定積分解けと言われたら初歩的なやつだったら解けるぐらいまで。 駆け足で3日ぐらいで期待値->分散->標準偏差->正規分布->確率密度関数->累積分布関数までやって、その中で積分が必要になったので微分->積分とやった感じ 駆け足だからこそだとは思うけど、一番思ったのは文字の意味がわからんという部分 σやμやE[X]、∫にdxといった文字がぞろぞろと数式では出てくるけれど、これは非常に数学っていう文化をひしひしと感じさせられた プログラマ的に言うと過度にワンラインなコードと言った感じで、アン・リーダブルと言えそう。 ただこの辺はデジタル空間っていう有限だけどそれを…

tomtom58’s blog•16日前
混合確率分布クラスタリングモデルの理論と実装 はじめに 前回混合ガウスモデル(GMM)に関する記事を書かさせていただきました。今回は、混合ガウスモデルから考え方を派生させて、クラスタリングに使用する各変数によって、仮定する確率分布を柔軟に変化させ、柔軟な確率的アプローチなクラスタリングを実装できないかというのが今回の、記事の趣旨になってきます。この発想自体は、私の発想ではなく、仕事の中で同僚が考えた方法であり、私はそれを少し聞きかじった程度の状態で、自分の中で想像を膨らませ、今回考えた手法(仮に混合確率分布モデルとする)を理論と実装にわたり軽く記事にしてみようというのが今回の趣旨になってきます。 そもそも、GMM自体が近年流行してきている…
はじめに 前回混合ガウスモデル(GMM)に関する記事を書かさせていただきました。今回は、混合ガウスモデルから考え方を派生させて、クラスタリングに使用する各変数によって、仮定する確率分布を柔軟に変化させ、柔軟な確率的アプローチなクラスタリングを実装できないかというのが今回の、記事の趣旨になってきます。この発想自体は、私の発想ではなく、仕事の中で同僚が考えた方法であり、私はそれを少し聞きかじった程度の状態で、自分の中で想像を膨らませ、今回考えた手法(仮に混合確率分布モデルとする)を理論と実装にわたり軽く記事にしてみようというのが今回の趣旨になってきます。 そもそも、GMM自体が近年流行してきている…

jiku log•18日前
2024年10月の学びの振り返り はじめに 当ブログのサブタイトルは,「JTCのデータサイエンス中間管理職の学び」である。というわけで,10月の学習記録を振り返ってみた。 目次 はじめに 目次 インプット編 「大規模言語モデル入門」 「データ解析のための統計モデリング入門 一般化線形モデル・階層ベイズモデル・MCMC」 アウトプット編 振り返りと今後の抱負 インプットとアウトプットのバランスを考慮するべき 自分なりの切り口を見せたい インプット編 2024年10月は,2冊の本を読んだ。 「大規模言語モデル入門」 gihyo.jp職場の重点施策であり,近年着目されている技術である大規模言語モデルについて,代表的なアルゴリズムの特…
はじめに 当ブログのサブタイトルは,「JTCのデータサイエンス中間管理職の学び」である。というわけで,10月の学習記録を振り返ってみた。 目次 はじめに 目次 インプット編 「大規模言語モデル入門」 「データ解析のための統計モデリング入門 一般化線形モデル・階層ベイズモデル・MCMC」 アウトプット編 振り返りと今後の抱負 インプットとアウトプットのバランスを考慮するべき 自分なりの切り口を見せたい インプット編 2024年10月は,2冊の本を読んだ。 「大規模言語モデル入門」 gihyo.jp職場の重点施策であり,近年着目されている技術である大規模言語モデルについて,代表的なアルゴリズムの特…
初心者データサイエンティストの備忘録•22日前
【深層学習】パラメータの初期化手法をどのように選択すべきか?活性化関数に応じて決める はじめに 一般的に機械学習モデルを構築する際には、教師データからモデルが分類ルールを獲得する必要があります。この分類ルールを獲得することは「学習」と呼ばれ、機械学習モデルに含まれるパラメータを調整して損失関数を減少させることで実現します。つまり、機械学習モデルの学習とは、パラメータを入力とする損失関数の最小化問題を解くことにあたります。 深層学習における損失関数の最小化には、広く「勾配降下法」が使われます。勾配降下法は、初期値を設定し、その値を繰り返し更新して損失関数を最小化する手法です。そのため、最終的な結果の精度は、最初に設定する値、つまり初期値に大きく左右されます。この記事では「どのよう…
はじめに 一般的に機械学習モデルを構築する際には、教師データからモデルが分類ルールを獲得する必要があります。この分類ルールを獲得することは「学習」と呼ばれ、機械学習モデルに含まれるパラメータを調整して損失関数を減少させることで実現します。つまり、機械学習モデルの学習とは、パラメータを入力とする損失関数の最小化問題を解くことにあたります。 深層学習における損失関数の最小化には、広く「勾配降下法」が使われます。勾配降下法は、初期値を設定し、その値を繰り返し更新して損失関数を最小化する手法です。そのため、最終的な結果の精度は、最初に設定する値、つまり初期値に大きく左右されます。この記事では「どのよう…

vicarの日記•23日前
勉強用 80/20の法則 コントロール・プロセスに関して、多くの問題や欠陥(通常は80%)が少数の原因(通常は20%)によって引き起こされる一般的なガイドライン。「パレート図」参照。 A/Bテスト 一つの独立変数だけを変えた二つの類似サービスを示してユーザーの好みを調べるマーケティング手法。 Certified Associate in Project Management(CAPM) プロジェクトマネジメントに関心がある、またはキャリアをスタートしたばかりの実務者が受ける資格認定。PMBOK®ガイドの原理と用語についての知識を問う。 Completion Contract ベンダーがバイヤーにプロダ…
80/20の法則 コントロール・プロセスに関して、多くの問題や欠陥(通常は80%)が少数の原因(通常は20%)によって引き起こされる一般的なガイドライン。「パレート図」参照。 A/Bテスト 一つの独立変数だけを変えた二つの類似サービスを示してユーザーの好みを調べるマーケティング手法。 Certified Associate in Project Management(CAPM) プロジェクトマネジメントに関心がある、またはキャリアをスタートしたばかりの実務者が受ける資格認定。PMBOK®ガイドの原理と用語についての知識を問う。 Completion Contract ベンダーがバイヤーにプロダ…

jiku log•25日前
統計検定1級に合格して変わらなかったこと・変わったこと #統計検定 はじめに 先日,「名刺に『統計検定1級(理工学)』と入れた話」をXにポストしたところ,多くの方から反応を頂けた。 名刺に「統計検定1級(理工学)」と入れたが反応が無かった話 拙者,名刺に「統計検定1級(理工学)」って書いて,ご丁寧にQRコードも入れてるのに,名刺を渡したお客さまからコメント・反応を頂いたことが無い。 https://t.co/71bRqrjU4i— yoshi.s (@stern_bow) 2024年10月20日 ↓ その2日後に,名刺に「統計検定1級(理工学)」と入れたことに反応があった話 拙者,名刺に「統計検定1級(理工学)」と書いているのだが,今日人生で初めて,名刺をお渡…
はじめに 先日,「名刺に『統計検定1級(理工学)』と入れた話」をXにポストしたところ,多くの方から反応を頂けた。 名刺に「統計検定1級(理工学)」と入れたが反応が無かった話 拙者,名刺に「統計検定1級(理工学)」って書いて,ご丁寧にQRコードも入れてるのに,名刺を渡したお客さまからコメント・反応を頂いたことが無い。 https://t.co/71bRqrjU4i— yoshi.s (@stern_bow) 2024年10月20日 ↓ その2日後に,名刺に「統計検定1級(理工学)」と入れたことに反応があった話 拙者,名刺に「統計検定1級(理工学)」と書いているのだが,今日人生で初めて,名刺をお渡…

jiku log•1ヶ月前
尤度比検定におけるカイ2乗分布の導出 #統計検定 はじめに 統計検定1級の統計数理・理工学において,尤度比検定は2012年~2022年の間で2回しか登場していないが,最尤法の漸近論で登場する統計的検定の手法として重要な内容である。尤度比の検定統計量はカイ2乗分布にしたがうが,これを導出する際につまずくことがあったので,手順について整理してみた。 目次 はじめに 目次 尤度比検定 統計検定1級での出題 尤度比検定統計量 尤度比検定におけるカイ2乗分布の導出 Step 1. テイラー展開 Step 2. 1次微分の項の式変形 Step 3. 2次微分の項の式変形 Step 3-1. フィッシャー情報量と大数の法則 Step 3-2. 最尤推定量の…
はじめに 統計検定1級の統計数理・理工学において,尤度比検定は2012年~2022年の間で2回しか登場していないが,最尤法の漸近論で登場する統計的検定の手法として重要な内容である。尤度比の検定統計量はカイ2乗分布にしたがうが,これを導出する際につまずくことがあったので,手順について整理してみた。 目次 はじめに 目次 尤度比検定 統計検定1級での出題 尤度比検定統計量 尤度比検定におけるカイ2乗分布の導出 Step 1. テイラー展開 Step 2. 1次微分の項の式変形 Step 3. 2次微分の項の式変形 Step 3-1. フィッシャー情報量と大数の法則 Step 3-2. 最尤推定量の…

jiku log•1ヶ月前
「データ解析のための統計モデリング入門」を読む ~第3章 一般化線形モデル(GLM)~ はじめに 数理統計学より実践的な内容の理解に向けて,久保 拓弥 著「データ解析のための統計モデリング入門 一般化線形モデル・階層ベイズモデル・MCMC」を読んでいる。本記事は,第3章「一般化線形モデル(GLM)」の読書メモである。なおPythonコードは,ChatGPT 3.5を用いて作成し,動作確認を行なっている。 本書の紹介ページ www.iwanami.co.jp 本書のサポートページ 生態学データ解析 - 本/データ解析のための統計モデリング入門 目次 はじめに 目次 第3章 一般化線形モデル(GLM) ―ポアソン回帰― 3.1 例題 : 個体ごとに平均種子数が異なる場合 3.2 観測…
はじめに 数理統計学より実践的な内容の理解に向けて,久保 拓弥 著「データ解析のための統計モデリング入門 一般化線形モデル・階層ベイズモデル・MCMC」を読んでいる。本記事は,第3章「一般化線形モデル(GLM)」の読書メモである。なおPythonコードは,ChatGPT 3.5を用いて作成し,動作確認を行なっている。 本書の紹介ページ www.iwanami.co.jp 本書のサポートページ 生態学データ解析 - 本/データ解析のための統計モデリング入門 目次 はじめに 目次 第3章 一般化線形モデル(GLM) ―ポアソン回帰― 3.1 例題 : 個体ごとに平均種子数が異なる場合 3.2 観測…

jiku log•1ヶ月前
ワルド検定とスコア検定の比較 #統計検定 はじめに 統計検定1級の統計数理・理工学において,ワルド検定・スコア検定はこれまでほとんど登場していないが,最尤法の漸近論で登場する統計的検定の手法としては重要な内容である。覚えようとしたときにごっちゃになってしまうことがあったので,両者を比較しながらまとめてみた。 目次 はじめに 目次 ワルド検定とスコア検定 統計検定1級での出題 ワルド検定とスコア検定の比較表 ワルド検定の詳細 背景にある性質 検定方式 スコア検定の詳細 背景にある性質 検定方式 ワルド検定とスコア検定の比較 まとめ ワルド検定とスコア検定 統計検定1級での出題 統計検定1級の統計数理・理工学において,2012年~2022…
はじめに 統計検定1級の統計数理・理工学において,ワルド検定・スコア検定はこれまでほとんど登場していないが,最尤法の漸近論で登場する統計的検定の手法としては重要な内容である。覚えようとしたときにごっちゃになってしまうことがあったので,両者を比較しながらまとめてみた。 目次 はじめに 目次 ワルド検定とスコア検定 統計検定1級での出題 ワルド検定とスコア検定の比較表 ワルド検定の詳細 背景にある性質 検定方式 スコア検定の詳細 背景にある性質 検定方式 ワルド検定とスコア検定の比較 まとめ ワルド検定とスコア検定 統計検定1級での出題 統計検定1級の統計数理・理工学において,2012年~2022…

jiku log•1ヶ月前
独立した合成変数を用いたt分布の平均・分散の導出 #統計検定 はじめに 統計検定1級の統計数理・理工学において,t分布はこれまで3回出てきた。標本分布や統計的検定においてお馴染みの分野ではあるが,「t分布にしたがう変数は,独立した確率変数の合成(積)である」という性質から,平均・分散が導出できることを説明する。 目次 はじめに 目次 t分布 統計検定1級での出題 定義 確率密度関数 t分布の平均・分散の導出 方針 平均の導出 分散の導出 まとめ t分布 統計検定1級での出題 統計検定1級の統計数理・理工学において,2012年~2022年の10年の間で,関連する問題が3題出題されている。 定義 t分布は,正規母集団から作られる統計量の分布として代表的なもの…
はじめに 統計検定1級の統計数理・理工学において,t分布はこれまで3回出てきた。標本分布や統計的検定においてお馴染みの分野ではあるが,「t分布にしたがう変数は,独立した確率変数の合成(積)である」という性質から,平均・分散が導出できることを説明する。 目次 はじめに 目次 t分布 統計検定1級での出題 定義 確率密度関数 t分布の平均・分散の導出 方針 平均の導出 分散の導出 まとめ t分布 統計検定1級での出題 統計検定1級の統計数理・理工学において,2012年~2022年の10年の間で,関連する問題が3題出題されている。 定義 t分布は,正規母集団から作られる統計量の分布として代表的なもの…

Kosのひとりごと•1ヶ月前
生物学専攻が泣きながら情報学専攻を受験した話 【電通大 院試】 やあこんにちは、Kosです。記事を書くのは初めてだと思ったら2年前にサークル企画で書いてた。ついでに未投稿の下書き見つけた。 今回は「生物学専攻が泣きながら情報学専攻を受験した話」ということで、院試期間何をしていたかを書いてみようと思います。ちょっと珍しい状況なので、専攻を大きく変える後輩達の役に立てたらと思います。そうじゃない人にはちょっとしたおもしろ読み物と思っていただければ幸いです。 1万字ちょい書きましたが内容の大部分が勉強部なので院試終了フレンズにとっては読みごたえはないかも。 ではでは 一番大事な書き忘れ追記:受かってました 自己紹介 なんで専攻変えたの? 意気込み? 実は0次試験…
やあこんにちは、Kosです。記事を書くのは初めてだと思ったら2年前にサークル企画で書いてた。ついでに未投稿の下書き見つけた。 今回は「生物学専攻が泣きながら情報学専攻を受験した話」ということで、院試期間何をしていたかを書いてみようと思います。ちょっと珍しい状況なので、専攻を大きく変える後輩達の役に立てたらと思います。そうじゃない人にはちょっとしたおもしろ読み物と思っていただければ幸いです。 1万字ちょい書きましたが内容の大部分が勉強部なので院試終了フレンズにとっては読みごたえはないかも。 ではでは 一番大事な書き忘れ追記:受かってました 自己紹介 なんで専攻変えたの? 意気込み? 実は0次試験…

理系会社員のスキルメモ•1ヶ月前
確率変数の和-1 確率変数の和 独立な確率変数 の和 の確率密度関数 は以下のとおり表せる: また、分布関数 は以下のとおり: 具体的には以下の3-stepsで求めることができる。 なお、確率変数の差、積、商の確率密度関数についてもこの考え方を適用できる。 と変換するとき、そのJacobianは となる。 の同時密度関数は、 である。 これを に関して積分すればok。 ちなみに、再生性をもつ分布例は以下のとおり: 二項分布 ポアソン分布 負の二項分布 正規分布 ガンマ分布 計算例 一様分布の和 独立な確率変数 がともに一様分布 に従うときの の確率密度関数を求める。 以下共通部分で積分することで求めることができ…
確率変数の和 独立な確率変数 の和 の確率密度関数 は以下のとおり表せる: また、分布関数 は以下のとおり: 具体的には以下の3-stepsで求めることができる。 なお、確率変数の差、積、商の確率密度関数についてもこの考え方を適用できる。 と変換するとき、そのJacobianは となる。 の同時密度関数は、 である。 これを に関して積分すればok。 ちなみに、再生性をもつ分布例は以下のとおり: 二項分布 ポアソン分布 負の二項分布 正規分布 ガンマ分布 計算例 一様分布の和 独立な確率変数 がともに一様分布 に従うときの の確率密度関数を求める。 以下共通部分で積分することで求めることができ…

jiku log•1ヶ月前
クラメール・ラオの不等式の導出の流れとその応用 #統計検定 はじめに 統計検定1級の統計数理・理工学において,クラメール・ラオの不等式やフィッシャー情報量の話題は2回しか出たことがないテーマではあるが,数理統計学のテキストにはよく出てくる話題である。クラメール・ラオの不等式の不等式は,不偏推定量の分散の下限を与える重要な式であるが,証明の流れがごちゃごちゃしていたので,整理してみた。 目次 はじめに 目次 クラメール・ラオの不等式 定義 方針 導出 Step 1. フィッシャー情報量【定義式】 Step 2. 確率密度関数の積分【定義式】 Step 3. 確率密度関数の微分【パラメータによる微分】 Step 4. スコア関数の期待値【パラメータによる微…
はじめに 統計検定1級の統計数理・理工学において,クラメール・ラオの不等式やフィッシャー情報量の話題は2回しか出たことがないテーマではあるが,数理統計学のテキストにはよく出てくる話題である。クラメール・ラオの不等式の不等式は,不偏推定量の分散の下限を与える重要な式であるが,証明の流れがごちゃごちゃしていたので,整理してみた。 目次 はじめに 目次 クラメール・ラオの不等式 定義 方針 導出 Step 1. フィッシャー情報量【定義式】 Step 2. 確率密度関数の積分【定義式】 Step 3. 確率密度関数の微分【パラメータによる微分】 Step 4. スコア関数の期待値【パラメータによる微…

jiku log•2ヶ月前
ベータ分布の正規近似 #統計検定 はじめに 統計検定1級の統計数理・理工学において,ベータ分布はこれまでに2回しか出たことがないテーマではあるが,数理統計学のテキストにはよく出てくる分布である。先日,ガンマ分布の正規近似とスターリングの公式 #統計検定 - jiku logという記事を紹介した。ガンマ分布を正規分布で近似する際に,スターリングの公式を導出するというものである。 似たような流れで,ベータ分布を正規分布で近似する手順を紹介する。 目次 はじめに 目次 ベータ分布の正規近似 方針 変数変換アプローチの全体像 導出 Step 1. 標準化の応用による確率変数の変数変換 Step 2. 変数を含む部分の変形 Step 3…
はじめに 統計検定1級の統計数理・理工学において,ベータ分布はこれまでに2回しか出たことがないテーマではあるが,数理統計学のテキストにはよく出てくる分布である。先日,ガンマ分布の正規近似とスターリングの公式 #統計検定 - jiku logという記事を紹介した。ガンマ分布を正規分布で近似する際に,スターリングの公式を導出するというものである。 似たような流れで,ベータ分布を正規分布で近似する手順を紹介する。 目次 はじめに 目次 ベータ分布の正規近似 方針 変数変換アプローチの全体像 導出 Step 1. 標準化の応用による確率変数の変数変換 Step 2. 変数を含む部分の変形 Step 3…

manabitimes.jp

ja.wikipedia.org

qiita.com
avilen.co.jp
dsl4.eee.u-ryukyu.ac.jp

manabitimes.jp
yagays.github.io
![]()
gihyo.jp
 以前の記事に続き、統計検定1級/準1級の対策として、各確率分布の期待値・分散・母関数について整理しました。 今回は、連続分布を扱いました。 離散分布のまとめについてはこちらを参照ください。 確率分布の期待値・分散・母関数まとめ~離散分布~ - Kevin's Data Analytics Blog 1. 連続一様分布 定義 𝑎確率密度関数の値が常に一定であるような確率分布を連続一様分布という。 確率密度関数 期待値 分散 積率母関数(モーメント母関数) 2. 正規分布 定義 𝜇∈"ℝ, " σ>0とし、確率変数𝑋に対して、以下の確率密度関数をもつ分布を正規分布という。𝜇を中心する左右対称の釣鐘…
以前の記事に続き、統計検定1級/準1級の対策として、各確率分布の期待値・分散・母関数について整理しました。 今回は、連続分布を扱いました。 離散分布のまとめについてはこちらを参照ください。 確率分布の期待値・分散・母関数まとめ~離散分布~ - Kevin's Data Analytics Blog 1. 連続一様分布 定義 𝑎確率密度関数の値が常に一定であるような確率分布を連続一様分布という。 確率密度関数 期待値 分散 積率母関数(モーメント母関数) 2. 正規分布 定義 𝜇∈"ℝ, " σ>0とし、確率変数𝑋に対して、以下の確率密度関数をもつ分布を正規分布という。𝜇を中心する左右対称の釣鐘… ーーーーーーーー 主要内容 紹介書籍 正規分布や標準正規分布の縦軸 〖追記①:2021/9/1追記 〖追記②:2021/9/3追記 ーーーーーーーー 昔、統計検定2級に合格したんですが、だいぶ忘れてます。統計学入門的な内容から勉強し直してます。 正規分布や標準正規分布の図はおなじみの物だと思いますが、縦軸を省略しているものが多く、そういや縦軸を省略せずに表すとするとどんな表記になるんだろ?と思ってたことがあります。自分の備忘録として記載したいと思います。 表題について解決に導いてくれた3冊の書籍を紹介させていただきます。 ↓↓↓ 紹介書籍 紹介書籍①: 【リンク】⇒Amazon/通販/商品紹介…
ーーーーーーーー 主要内容 紹介書籍 正規分布や標準正規分布の縦軸 〖追記①:2021/9/1追記 〖追記②:2021/9/3追記 ーーーーーーーー 昔、統計検定2級に合格したんですが、だいぶ忘れてます。統計学入門的な内容から勉強し直してます。 正規分布や標準正規分布の図はおなじみの物だと思いますが、縦軸を省略しているものが多く、そういや縦軸を省略せずに表すとするとどんな表記になるんだろ?と思ってたことがあります。自分の備忘録として記載したいと思います。 表題について解決に導いてくれた3冊の書籍を紹介させていただきます。 ↓↓↓ 紹介書籍 紹介書籍①: 【リンク】⇒Amazon/通販/商品紹介… はじめに 最近私は、因果推論と並んでセミパラメトリック手法にとても興味関心を持っています。解釈したい部分はパラメトリックに、それ以外の部分はノンパラメトリックにといううたい文句はとても興味をそそられますよね。パラメトリックに規定して解釈性を担保するというのは、現実の実務においても多々やりますが、それ以外の解釈性が不要な部分に関して複雑な表現を許すことによって、複雑な事象のパラメトリックに定義した(基本線形)の係数値が正しい値になり得るということも考えられます。というわけで、非常にセミパラメトリック手法に私は期待を持っているわけです。 最近、私はセミパラメトリック手法の一種であるGAM(一般化法…
はじめに 最近私は、因果推論と並んでセミパラメトリック手法にとても興味関心を持っています。解釈したい部分はパラメトリックに、それ以外の部分はノンパラメトリックにといううたい文句はとても興味をそそられますよね。パラメトリックに規定して解釈性を担保するというのは、現実の実務においても多々やりますが、それ以外の解釈性が不要な部分に関して複雑な表現を許すことによって、複雑な事象のパラメトリックに定義した(基本線形)の係数値が正しい値になり得るということも考えられます。というわけで、非常にセミパラメトリック手法に私は期待を持っているわけです。 最近、私はセミパラメトリック手法の一種であるGAM(一般化法… 微積分までやった、理解度は低いけど定積分解けと言われたら初歩的なやつだったら解けるぐらいまで。 駆け足で3日ぐらいで期待値->分散->標準偏差->正規分布->確率密度関数->累積分布関数までやって、その中で積分が必要になったので微分->積分とやった感じ 駆け足だからこそだとは思うけど、一番思ったのは文字の意味がわからんという部分 σやμやE[X]、∫にdxといった文字がぞろぞろと数式では出てくるけれど、これは非常に数学っていう文化をひしひしと感じさせられた プログラマ的に言うと過度にワンラインなコードと言った感じで、アン・リーダブルと言えそう。 ただこの辺はデジタル空間っていう有限だけどそれを…
微積分までやった、理解度は低いけど定積分解けと言われたら初歩的なやつだったら解けるぐらいまで。 駆け足で3日ぐらいで期待値->分散->標準偏差->正規分布->確率密度関数->累積分布関数までやって、その中で積分が必要になったので微分->積分とやった感じ 駆け足だからこそだとは思うけど、一番思ったのは文字の意味がわからんという部分 σやμやE[X]、∫にdxといった文字がぞろぞろと数式では出てくるけれど、これは非常に数学っていう文化をひしひしと感じさせられた プログラマ的に言うと過度にワンラインなコードと言った感じで、アン・リーダブルと言えそう。 ただこの辺はデジタル空間っていう有限だけどそれを… はじめに 前回混合ガウスモデル(GMM)に関する記事を書かさせていただきました。今回は、混合ガウスモデルから考え方を派生させて、クラスタリングに使用する各変数によって、仮定する確率分布を柔軟に変化させ、柔軟な確率的アプローチなクラスタリングを実装できないかというのが今回の、記事の趣旨になってきます。この発想自体は、私の発想ではなく、仕事の中で同僚が考えた方法であり、私はそれを少し聞きかじった程度の状態で、自分の中で想像を膨らませ、今回考えた手法(仮に混合確率分布モデルとする)を理論と実装にわたり軽く記事にしてみようというのが今回の趣旨になってきます。 そもそも、GMM自体が近年流行してきている…
はじめに 前回混合ガウスモデル(GMM)に関する記事を書かさせていただきました。今回は、混合ガウスモデルから考え方を派生させて、クラスタリングに使用する各変数によって、仮定する確率分布を柔軟に変化させ、柔軟な確率的アプローチなクラスタリングを実装できないかというのが今回の、記事の趣旨になってきます。この発想自体は、私の発想ではなく、仕事の中で同僚が考えた方法であり、私はそれを少し聞きかじった程度の状態で、自分の中で想像を膨らませ、今回考えた手法(仮に混合確率分布モデルとする)を理論と実装にわたり軽く記事にしてみようというのが今回の趣旨になってきます。 そもそも、GMM自体が近年流行してきている… はじめに 当ブログのサブタイトルは,「JTCのデータサイエンス中間管理職の学び」である。というわけで,10月の学習記録を振り返ってみた。 目次 はじめに 目次 インプット編 「大規模言語モデル入門」 「データ解析のための統計モデリング入門 一般化線形モデル・階層ベイズモデル・MCMC」 アウトプット編 振り返りと今後の抱負 インプットとアウトプットのバランスを考慮するべき 自分なりの切り口を見せたい インプット編 2024年10月は,2冊の本を読んだ。 「大規模言語モデル入門」 gihyo.jp職場の重点施策であり,近年着目されている技術である大規模言語モデルについて,代表的なアルゴリズムの特…
はじめに 当ブログのサブタイトルは,「JTCのデータサイエンス中間管理職の学び」である。というわけで,10月の学習記録を振り返ってみた。 目次 はじめに 目次 インプット編 「大規模言語モデル入門」 「データ解析のための統計モデリング入門 一般化線形モデル・階層ベイズモデル・MCMC」 アウトプット編 振り返りと今後の抱負 インプットとアウトプットのバランスを考慮するべき 自分なりの切り口を見せたい インプット編 2024年10月は,2冊の本を読んだ。 「大規模言語モデル入門」 gihyo.jp職場の重点施策であり,近年着目されている技術である大規模言語モデルについて,代表的なアルゴリズムの特… はじめに 一般的に機械学習モデルを構築する際には、教師データからモデルが分類ルールを獲得する必要があります。この分類ルールを獲得することは「学習」と呼ばれ、機械学習モデルに含まれるパラメータを調整して損失関数を減少させることで実現します。つまり、機械学習モデルの学習とは、パラメータを入力とする損失関数の最小化問題を解くことにあたります。 深層学習における損失関数の最小化には、広く「勾配降下法」が使われます。勾配降下法は、初期値を設定し、その値を繰り返し更新して損失関数を最小化する手法です。そのため、最終的な結果の精度は、最初に設定する値、つまり初期値に大きく左右されます。この記事では「どのよう…
はじめに 一般的に機械学習モデルを構築する際には、教師データからモデルが分類ルールを獲得する必要があります。この分類ルールを獲得することは「学習」と呼ばれ、機械学習モデルに含まれるパラメータを調整して損失関数を減少させることで実現します。つまり、機械学習モデルの学習とは、パラメータを入力とする損失関数の最小化問題を解くことにあたります。 深層学習における損失関数の最小化には、広く「勾配降下法」が使われます。勾配降下法は、初期値を設定し、その値を繰り返し更新して損失関数を最小化する手法です。そのため、最終的な結果の精度は、最初に設定する値、つまり初期値に大きく左右されます。この記事では「どのよう… 80/20の法則 コントロール・プロセスに関して、多くの問題や欠陥(通常は80%)が少数の原因(通常は20%)によって引き起こされる一般的なガイドライン。「パレート図」参照。 A/Bテスト 一つの独立変数だけを変えた二つの類似サービスを示してユーザーの好みを調べるマーケティング手法。 Certified Associate in Project Management(CAPM) プロジェクトマネジメントに関心がある、またはキャリアをスタートしたばかりの実務者が受ける資格認定。PMBOK®ガイドの原理と用語についての知識を問う。 Completion Contract ベンダーがバイヤーにプロダ…
80/20の法則 コントロール・プロセスに関して、多くの問題や欠陥(通常は80%)が少数の原因(通常は20%)によって引き起こされる一般的なガイドライン。「パレート図」参照。 A/Bテスト 一つの独立変数だけを変えた二つの類似サービスを示してユーザーの好みを調べるマーケティング手法。 Certified Associate in Project Management(CAPM) プロジェクトマネジメントに関心がある、またはキャリアをスタートしたばかりの実務者が受ける資格認定。PMBOK®ガイドの原理と用語についての知識を問う。 Completion Contract ベンダーがバイヤーにプロダ… はじめに 先日,「名刺に『統計検定1級(理工学)』と入れた話」をXにポストしたところ,多くの方から反応を頂けた。 名刺に「統計検定1級(理工学)」と入れたが反応が無かった話 拙者,名刺に「統計検定1級(理工学)」って書いて,ご丁寧にQRコードも入れてるのに,名刺を渡したお客さまからコメント・反応を頂いたことが無い。 https://t.co/71bRqrjU4i— yoshi.s (@stern_bow) 2024年10月20日 ↓ その2日後に,名刺に「統計検定1級(理工学)」と入れたことに反応があった話 拙者,名刺に「統計検定1級(理工学)」と書いているのだが,今日人生で初めて,名刺をお渡…
はじめに 先日,「名刺に『統計検定1級(理工学)』と入れた話」をXにポストしたところ,多くの方から反応を頂けた。 名刺に「統計検定1級(理工学)」と入れたが反応が無かった話 拙者,名刺に「統計検定1級(理工学)」って書いて,ご丁寧にQRコードも入れてるのに,名刺を渡したお客さまからコメント・反応を頂いたことが無い。 https://t.co/71bRqrjU4i— yoshi.s (@stern_bow) 2024年10月20日 ↓ その2日後に,名刺に「統計検定1級(理工学)」と入れたことに反応があった話 拙者,名刺に「統計検定1級(理工学)」と書いているのだが,今日人生で初めて,名刺をお渡… はじめに 統計検定1級の統計数理・理工学において,尤度比検定は2012年~2022年の間で2回しか登場していないが,最尤法の漸近論で登場する統計的検定の手法として重要な内容である。尤度比の検定統計量はカイ2乗分布にしたがうが,これを導出する際につまずくことがあったので,手順について整理してみた。 目次 はじめに 目次 尤度比検定 統計検定1級での出題 尤度比検定統計量 尤度比検定におけるカイ2乗分布の導出 Step 1. テイラー展開 Step 2. 1次微分の項の式変形 Step 3. 2次微分の項の式変形 Step 3-1. フィッシャー情報量と大数の法則 Step 3-2. 最尤推定量の…
はじめに 統計検定1級の統計数理・理工学において,尤度比検定は2012年~2022年の間で2回しか登場していないが,最尤法の漸近論で登場する統計的検定の手法として重要な内容である。尤度比の検定統計量はカイ2乗分布にしたがうが,これを導出する際につまずくことがあったので,手順について整理してみた。 目次 はじめに 目次 尤度比検定 統計検定1級での出題 尤度比検定統計量 尤度比検定におけるカイ2乗分布の導出 Step 1. テイラー展開 Step 2. 1次微分の項の式変形 Step 3. 2次微分の項の式変形 Step 3-1. フィッシャー情報量と大数の法則 Step 3-2. 最尤推定量の… はじめに 数理統計学より実践的な内容の理解に向けて,久保 拓弥 著「データ解析のための統計モデリング入門 一般化線形モデル・階層ベイズモデル・MCMC」を読んでいる。本記事は,第3章「一般化線形モデル(GLM)」の読書メモである。なおPythonコードは,ChatGPT 3.5を用いて作成し,動作確認を行なっている。 本書の紹介ページ www.iwanami.co.jp 本書のサポートページ 生態学データ解析 - 本/データ解析のための統計モデリング入門 目次 はじめに 目次 第3章 一般化線形モデル(GLM) ―ポアソン回帰― 3.1 例題 : 個体ごとに平均種子数が異なる場合 3.2 観測…
はじめに 数理統計学より実践的な内容の理解に向けて,久保 拓弥 著「データ解析のための統計モデリング入門 一般化線形モデル・階層ベイズモデル・MCMC」を読んでいる。本記事は,第3章「一般化線形モデル(GLM)」の読書メモである。なおPythonコードは,ChatGPT 3.5を用いて作成し,動作確認を行なっている。 本書の紹介ページ www.iwanami.co.jp 本書のサポートページ 生態学データ解析 - 本/データ解析のための統計モデリング入門 目次 はじめに 目次 第3章 一般化線形モデル(GLM) ―ポアソン回帰― 3.1 例題 : 個体ごとに平均種子数が異なる場合 3.2 観測… はじめに 統計検定1級の統計数理・理工学において,ワルド検定・スコア検定はこれまでほとんど登場していないが,最尤法の漸近論で登場する統計的検定の手法としては重要な内容である。覚えようとしたときにごっちゃになってしまうことがあったので,両者を比較しながらまとめてみた。 目次 はじめに 目次 ワルド検定とスコア検定 統計検定1級での出題 ワルド検定とスコア検定の比較表 ワルド検定の詳細 背景にある性質 検定方式 スコア検定の詳細 背景にある性質 検定方式 ワルド検定とスコア検定の比較 まとめ ワルド検定とスコア検定 統計検定1級での出題 統計検定1級の統計数理・理工学において,2012年~2022…
はじめに 統計検定1級の統計数理・理工学において,ワルド検定・スコア検定はこれまでほとんど登場していないが,最尤法の漸近論で登場する統計的検定の手法としては重要な内容である。覚えようとしたときにごっちゃになってしまうことがあったので,両者を比較しながらまとめてみた。 目次 はじめに 目次 ワルド検定とスコア検定 統計検定1級での出題 ワルド検定とスコア検定の比較表 ワルド検定の詳細 背景にある性質 検定方式 スコア検定の詳細 背景にある性質 検定方式 ワルド検定とスコア検定の比較 まとめ ワルド検定とスコア検定 統計検定1級での出題 統計検定1級の統計数理・理工学において,2012年~2022… はじめに 統計検定1級の統計数理・理工学において,t分布はこれまで3回出てきた。標本分布や統計的検定においてお馴染みの分野ではあるが,「t分布にしたがう変数は,独立した確率変数の合成(積)である」という性質から,平均・分散が導出できることを説明する。 目次 はじめに 目次 t分布 統計検定1級での出題 定義 確率密度関数 t分布の平均・分散の導出 方針 平均の導出 分散の導出 まとめ t分布 統計検定1級での出題 統計検定1級の統計数理・理工学において,2012年~2022年の10年の間で,関連する問題が3題出題されている。 定義 t分布は,正規母集団から作られる統計量の分布として代表的なもの…
はじめに 統計検定1級の統計数理・理工学において,t分布はこれまで3回出てきた。標本分布や統計的検定においてお馴染みの分野ではあるが,「t分布にしたがう変数は,独立した確率変数の合成(積)である」という性質から,平均・分散が導出できることを説明する。 目次 はじめに 目次 t分布 統計検定1級での出題 定義 確率密度関数 t分布の平均・分散の導出 方針 平均の導出 分散の導出 まとめ t分布 統計検定1級での出題 統計検定1級の統計数理・理工学において,2012年~2022年の10年の間で,関連する問題が3題出題されている。 定義 t分布は,正規母集団から作られる統計量の分布として代表的なもの… やあこんにちは、Kosです。記事を書くのは初めてだと思ったら2年前にサークル企画で書いてた。ついでに未投稿の下書き見つけた。 今回は「生物学専攻が泣きながら情報学専攻を受験した話」ということで、院試期間何をしていたかを書いてみようと思います。ちょっと珍しい状況なので、専攻を大きく変える後輩達の役に立てたらと思います。そうじゃない人にはちょっとしたおもしろ読み物と思っていただければ幸いです。 1万字ちょい書きましたが内容の大部分が勉強部なので院試終了フレンズにとっては読みごたえはないかも。 ではでは 一番大事な書き忘れ追記:受かってました 自己紹介 なんで専攻変えたの? 意気込み? 実は0次試験…
やあこんにちは、Kosです。記事を書くのは初めてだと思ったら2年前にサークル企画で書いてた。ついでに未投稿の下書き見つけた。 今回は「生物学専攻が泣きながら情報学専攻を受験した話」ということで、院試期間何をしていたかを書いてみようと思います。ちょっと珍しい状況なので、専攻を大きく変える後輩達の役に立てたらと思います。そうじゃない人にはちょっとしたおもしろ読み物と思っていただければ幸いです。 1万字ちょい書きましたが内容の大部分が勉強部なので院試終了フレンズにとっては読みごたえはないかも。 ではでは 一番大事な書き忘れ追記:受かってました 自己紹介 なんで専攻変えたの? 意気込み? 実は0次試験… 確率変数の和 独立な確率変数 の和 の確率密度関数 は以下のとおり表せる: また、分布関数 は以下のとおり: 具体的には以下の3-stepsで求めることができる。 なお、確率変数の差、積、商の確率密度関数についてもこの考え方を適用できる。 と変換するとき、そのJacobianは となる。 の同時密度関数は、 である。 これを に関して積分すればok。 ちなみに、再生性をもつ分布例は以下のとおり: 二項分布 ポアソン分布 負の二項分布 正規分布 ガンマ分布 計算例 一様分布の和 独立な確率変数 がともに一様分布 に従うときの の確率密度関数を求める。 以下共通部分で積分することで求めることができ…
確率変数の和 独立な確率変数 の和 の確率密度関数 は以下のとおり表せる: また、分布関数 は以下のとおり: 具体的には以下の3-stepsで求めることができる。 なお、確率変数の差、積、商の確率密度関数についてもこの考え方を適用できる。 と変換するとき、そのJacobianは となる。 の同時密度関数は、 である。 これを に関して積分すればok。 ちなみに、再生性をもつ分布例は以下のとおり: 二項分布 ポアソン分布 負の二項分布 正規分布 ガンマ分布 計算例 一様分布の和 独立な確率変数 がともに一様分布 に従うときの の確率密度関数を求める。 以下共通部分で積分することで求めることができ… はじめに 統計検定1級の統計数理・理工学において,クラメール・ラオの不等式やフィッシャー情報量の話題は2回しか出たことがないテーマではあるが,数理統計学のテキストにはよく出てくる話題である。クラメール・ラオの不等式の不等式は,不偏推定量の分散の下限を与える重要な式であるが,証明の流れがごちゃごちゃしていたので,整理してみた。 目次 はじめに 目次 クラメール・ラオの不等式 定義 方針 導出 Step 1. フィッシャー情報量【定義式】 Step 2. 確率密度関数の積分【定義式】 Step 3. 確率密度関数の微分【パラメータによる微分】 Step 4. スコア関数の期待値【パラメータによる微…
はじめに 統計検定1級の統計数理・理工学において,クラメール・ラオの不等式やフィッシャー情報量の話題は2回しか出たことがないテーマではあるが,数理統計学のテキストにはよく出てくる話題である。クラメール・ラオの不等式の不等式は,不偏推定量の分散の下限を与える重要な式であるが,証明の流れがごちゃごちゃしていたので,整理してみた。 目次 はじめに 目次 クラメール・ラオの不等式 定義 方針 導出 Step 1. フィッシャー情報量【定義式】 Step 2. 確率密度関数の積分【定義式】 Step 3. 確率密度関数の微分【パラメータによる微分】 Step 4. スコア関数の期待値【パラメータによる微… はじめに 統計検定1級の統計数理・理工学において,ベータ分布はこれまでに2回しか出たことがないテーマではあるが,数理統計学のテキストにはよく出てくる分布である。先日,ガンマ分布の正規近似とスターリングの公式 #統計検定 - jiku logという記事を紹介した。ガンマ分布を正規分布で近似する際に,スターリングの公式を導出するというものである。 似たような流れで,ベータ分布を正規分布で近似する手順を紹介する。 目次 はじめに 目次 ベータ分布の正規近似 方針 変数変換アプローチの全体像 導出 Step 1. 標準化の応用による確率変数の変数変換 Step 2. 変数を含む部分の変形 Step 3…
はじめに 統計検定1級の統計数理・理工学において,ベータ分布はこれまでに2回しか出たことがないテーマではあるが,数理統計学のテキストにはよく出てくる分布である。先日,ガンマ分布の正規近似とスターリングの公式 #統計検定 - jiku logという記事を紹介した。ガンマ分布を正規分布で近似する際に,スターリングの公式を導出するというものである。 似たような流れで,ベータ分布を正規分布で近似する手順を紹介する。 目次 はじめに 目次 ベータ分布の正規近似 方針 変数変換アプローチの全体像 導出 Step 1. 標準化の応用による確率変数の変数変換 Step 2. 変数を含む部分の変形 Step 3…