Schwarzer Körper (original) (raw)

Ein Schwarzer Körper (auch: Schwarzer Strahler, planckscher Strahler, idealer schwarzer Körper) ist eine idealisierte thermische Strahlungsquelle. Die Idealisierung besteht darin, dass solch ein Körper alle auftreffende elektromagnetische Strahlung jeglicher Wellenlänge vollständig absorbiert, während reale Körper immer einen Teil davon zurückwerfen. Gleichzeitig sendet er als Wärmestrahlung eine elektromagnetische Strahlung aus, deren Intensität und spektrale Verteilung von der weiteren Beschaffenheit des Körpers und seiner Oberfläche unabhängig sind und nur von seiner Temperatur abhängen.

Die Wärmestrahlung des schwarzen Körpers ist in jedem Wellenlängenbereich stärker als die eines jeden realen Körpers gleicher Fläche und gleicher Temperatur. Sie wird Schwarzkörperstrahlung oder aufgrund der Realisierung des schwarzen Körpers durch einen Hohlraum auch Hohlraumstrahlung genannt. In der Literatur des späten 19. und des frühen 20. Jahrhunderts ist die Bezeichnung schwarze Strahlung zu finden.

Der schwarze Körper dient als Grundlage für theoretische Betrachtungen sowie als Referenz für praktische Untersuchungen elektromagnetischer Strahlung. Der Begriff „Schwarzer Körper“ wurde 1860 von Gustav Robert Kirchhoff geprägt.

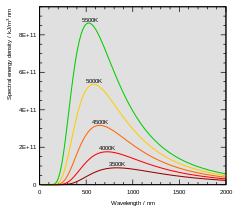
Spektrale Verteilung der Intensität der Schwarzkörperstrahlung

Strahlungsleistung und Wellenlängenemissionen von schwarzen Strahlern bei bestimmten Temperaturen.

Ein Schwarzer Körper absorbiert auftreffende elektromagnetische Strahlung vollständig, somit auch Licht. Er lässt keine Strahlung hindurch und spiegelt oder streut nichts. Außer bei der Temperatur des absoluten Nullpunkts sendet der Schwarze Körper eine als Wärmestrahlung (oder thermische Strahlung, Schwarze Strahlung) bezeichnete elektromagnetische Strahlung aus. Intensität und spektrale Verteilung der Wärmestrahlung hängen nur von der Temperatur des Schwarzen Körpers ab, seine Material- und Oberflächeneigenschaften haben keinen Einfluss. Die Strahldichte der ausgesendeten Strahlung ist in allen Richtungen gleich (Lambert-Strahler). Die Strahlung eines Schwarzen Körpers dient bei der Beschreibung anderer Strahlungsquellen als Vergleich.

Nach dem kirchhoffschen Strahlungsgesetz ist für jeden realen Körper bei jeder Wellenlänge und in jeder Richtung das Emissionsvermögen für Wärmestrahlung proportional zu seinem Absorptionsvermögen. Da der Schwarze Körper bei jeder Wellenlänge das größtmögliche Absorptionsvermögen besitzt, gilt das auch für sein Emissionsvermögen. Bei keiner Wellenlänge oder Temperatur kann ein beliebiger realer Körper mehr thermische Strahlung aussenden als ein Schwarzer Körper.

Intensität und Frequenzverteilung der von einem Schwarzen Körper ausgesandten elektromagnetischen Strahlung werden durch das Plancksche Strahlungsgesetz (nach Max Planck) beschrieben. Mit steigender Temperatur verschiebt sich das Maximum der Frequenzverteilung zu höheren Frequenzen, also zu kürzeren Wellenlängen (Wiensches Verschiebungsgesetz). Das Stefan-Boltzmann-Gesetz beschreibt die gesamte abgestrahlte Energie, die proportional zur vierten Potenz der absoluten Temperatur des Schwarzen Körpers ist.

Ein Schwarzer Körper emittiert bei einer Temperatur von 300 K eine Strahlungsleistung von etwa 460 W/m². Für den Wellenlängenbereich, der dieser Temperatur entspricht, ist das Auge nicht empfindlich und der Schwarze Körper erscheint dunkel. Bei 5800 K (Temperatur der Sonnenoberfläche) emittiert ein Schwarzer Körper eine Strahlungsleistung von 64 MW/m². Bei dieser Temperatur liegt ein großer Teil der Strahlung im sichtbaren Spektralbereich, der Körper erscheint dem Auge weiß leuchtend. Einige Abstrahl-Leistungen bei verschiedenen Temperaturen sind in der Tabelle rechts angegeben.

Abstrahlung bedeutet Energieverlust und Abkühlung des Körpers. In realer Umgebung ist dabei auch die Einstrahlung aus der Umgebung zu berücksichtigen, beispielsweise bei Sonnenschein auf einen Körper.

Abstrahl-Leistung einesschwarzen Strahlers[1]

Temperatur	Abstrahlung
°C	K	W/m²
−100	173	50
−50	223	140
0	273	314
50	323	617
100	373	1097
200	473	2838
300	573	6112
400	673	11631
500	773	20244
600	873	32933
700	973	50819
800	1073	75159
900	1173	107343

Der Versuch, die Schwarzkörperstrahlung theoretisch zu beschreiben, hat wesentlich zur Entstehung der Quantenphysik beigetragen. So divergiert bei einer rein klassischen Beschreibung die Schwarzkörperstrahlung im UV-Bereich (die sog. Ultraviolett-Katastrophe). Erst die Annahme von Max Planck im Jahr 1900, dass die Materie die Strahlungsenergie nur in Form bestimmter Energiequanten aufnehmen und abgeben kann, konnte dieses Rätsel lösen.

Ein idealer Schwarzer Körper lässt sich nicht verwirklichen. Es sind keine Materialien bekannt, die elektromagnetische Wellen frequenzunabhängig vollständig absorbieren. Eine berußte Oberfläche hat zwar im sichtbaren Spektralbereich einen Absorptionsgrad von ca. 0,96 – bei anderen Wellenlängen jedoch nicht. Viele nichtmetallische Stoffe haben im Mittleren Infrarot einen hohen Absorptionsgrad, können jedoch im Sichtbaren weiß erscheinen (zum Beispiel Wandfarbe).

In der Regel sind nur die Absorptions- und Emissionseigenschaften der Strahlungsquelle von Interesse, nicht jedoch deren Form. Anstelle einer Oberfläche wird deshalb die Öffnung eines Hohlraumstrahlers oder einfach ein langes Sackloch verwendet. Damit lassen sich die idealen Eigenschaften eines Schwarzen Strahlers besser darstellen, auch wenn die inneren Oberflächen einen niedrigen Absorptionsgrad besitzen.[2]

In einem warmen Hohlraum mit Wänden aus beliebigem, nichttransparentem Material, die auf einer konstanten Temperatur gehalten werden, geben die Wände Wärmestrahlung ab und es stellt sich ein Strahlungsgleichgewicht ein.[2] Die elektromagnetische Strahlung, die den Hohlraum erfüllt, nennt man Hohlraumstrahlung. Die Energiedichte und die Frequenzverteilung der Hohlraumstrahlung hängt nur von der Temperatur der Wände ab und weist dieselbe Energiedichte und dasselbe Spektrum wie die Strahlung eines Schwarzen Körpers auf. Außerdem ist die Strahlung homogen, isotrop, unpolarisiert und vom Volumen des Hohlraums unabhängig und daher vollständig äquivalent zur Schwarzkörperstrahlung.

Modell eines schwarzen Körpers. Ein sehr kleines Loch lässt jede beliebige Strahlung in einen Hohlkörper hinein, aber nur thermische Strahlung hinaus.

Bringt man in der Hohlraumwand eine Öffnung an, die klein genug ist, um das thermische Gleichgewicht nicht merklich zu stören, so absorbiert das Loch nahezu ideal die einfallende Strahlung, und durch die Öffnung tritt nur thermische Strahlung aus. Die von der Öffnung ausgehende Strahlung hat dann die Eigenschaften eines Schwarzen Körpers, wenn die Öffnung klein gegenüber dem Innenvolumen ist. Dabei kann der Reflexionsgrad der inneren Hohlraumoberfläche wesentlich größer als null sein. Von außen in den Hohlraum einfallende Strahlung wird dann im Inneren vielfach hin und her reflektiert und dabei zum größten Teil absorbiert und nur zu einem kleinen Rest wieder durch Reflexionen ausgestrahlt. Solche Öffnungen erscheinen praktisch völlig schwarz. Zur Unterstützung der Absorption werden die Hohlraumwände wenn möglich schwarz und rau gestaltet. In der Praxis verwendete Schwarze Strahler sind Hohlkugeln mit einer Öffnung oder einseitig offene hohle Zylinder.

Schwarze Strahler für hohe Temperaturen (z. B. bis 1800 K, also ungefähr 1500 °C) bestehen innen aus keramischen Werkstoffen. Für die thermische Bestimmung der Strahlungsleistung von Laserstrahlen werden oft Absorptionskörper in Form von Hohlkegeln verwendet. Absorbierende Beschichtungen richten sich nach der zu messenden Wellenlänge.

Schwarze Strahler werden als Strahlungsquelle bzw. Strahlungsnormal für physikalische Untersuchungen (hier meist Hohlraumstrahler) und in Interferometern (keramische Strahler für das mittlere Infrarot) verwendet.
Laser-Leistungsmesser verwenden oft Hohlraum-Absorber zur thermischen bzw. kalorimetrischen Bestimmung der Laserstrahl-Leistung: Solche Absorber erhöhen die Messgenauigkeit und vermeiden gefährliche Streustrahlung. Sie werden daher auch als „Strahlenfalle“ eingesetzt.
In Brennöfen können Temperaturen mit durch kleine Sichtfenster gerichteten Pyrometern bestimmt werden – der Ofenraum bildet einen Schwarzen Strahler (Hohlraumstrahler). Die Oberfläche von Körpern kann zur emissionsgradunabhängigen Temperaturmessung mit einem Pyrometer mit einem Sackloch versehen werden, in welches das Pyrometer „blickt“.
Viele nichtmetallische Materialien haben für Wellenlängen, die größer als etwa 3 bis 5 μm sind, einen hohen Emissionsgrad im Bereich von 0,85 bis 0,95. Soll das Strahlungsverhalten bei niedrigen Temperaturen bestimmt werden (bei Raumtemperatur liegt das thermische Strahlungsmaximum bei 10 μm und damit in dem betreffenden Wellenlängenbereich), so können sie näherungsweise als Graue Körper, bei geringeren Genauigkeitsansprüchen auch als Schwarze Körper betrachtet werden.
Ruß ist in einem bestimmten Wellenlängenbereich eine gute Annäherung an einen Schwarzen Körper. Er erreicht je nach Konsistenz einen Absorptions- bzw. Emissionsgrad von ca. 0,96 und sein Emissionsgrad ist fast unabhängig von der Wellenlänge.
Menschliche Haut hat im Wellenlängenbereich zwischen 2 und 14 μm einen relativ konstanten Emissionsgrad zwischen ca. 0,97 und 0,98,[3] sie strahlt bei Körpertemperatur (Emissionsmaximum 9,4 μm) also fast wie ein Schwarzer Strahler und absorbiert die gesamte auffallende langwellige Wärmestrahlung aus der Umgebung (die Absorptionseigenschaften im sichtbaren Spektralbereich verhalten sich dagegen deutlich anders). Die pyrometrische Fiebermessung im Ohr (Messwellenlänge im mittleren Infrarot) findet nahezu einen Schwarzen Hohlraumstrahler vor.
Die kosmische Hintergrundstrahlung ist in sehr guter Näherung eine Schwarzkörperstrahlung mit einer Temperatur von 2,725 ± 0,002 Kelvin.
In der Astronomie werden Sterne oft durch Schwarze Körper approximiert, daraus bestimmt man ihre effektive Oberflächentemperatur.

Man betrachte einen evakuierten Hohlraum mit Wänden aus beliebigem nichttransparentem Material, die auf einer konstanten Temperatur T {\displaystyle T} $T$ gehalten werden. Die Wände geben Wärmestrahlung ab und es wird sich nach hinreichender Zeit ein thermischer Gleichgewichtszustand einstellen.

Die Energiedichte im Hohlraum hängt nicht von der Beschaffenheit der Wände ab. Zum Beweis verbinde man zwei Hohlräume, deren Wände unterschiedliche Strahlungseigenschaften, aber gleiche Temperaturen haben, durch eine Öffnung miteinander. Ein Farbfilter in der Öffnung lasse nur Strahlung der Frequenz ν {\displaystyle \nu } $\nu$ passieren. Durch die Öffnung wird Strahlung zwischen den Hohlräumen ausgetauscht. Wäre die spektrale Energiedichte bei der Frequenz ν {\displaystyle \nu } $\nu$ in einem Hohlraum höher, so würde mehr Strahlung in den energieärmeren Hohlraum fließen als umgekehrt und die Energiedichte und damit die Temperatur würde im zweiten Hohlraum zunehmen. Diese spontane Entstehung einer Temperaturdifferenz widerspräche aber dem Zweiten Hauptsatz der Thermodynamik. Daher müssen die spektralen Energiedichten bei allen Frequenzen und somit auch die gesamte Energiedichte in beiden Hohlräumen identisch sein.

Auf ähnliche Weise lässt sich zeigen, dass die Strahlung im Hohlraum homogen, isotrop, unpolarisiert und vom Volumen des Hohlraums unabhängig sein muss.

Die spektrale Energiedichte U ν {\displaystyle U_{\nu }} $U_{\nu }$ im Hohlraum stellt also eine nur von der Frequenz und Temperatur abhängige universelle Funktion dar:

U ν ( ν , T ) = U ν 0 ( ν , T ) = 8 π h ν 3 c 3 1 e h ν / k T − 1 {\displaystyle U_{\nu }(\nu ,T)=U_{\nu }^{0}(\nu ,T)={\frac {8\pi h\nu ^{3}}{c^{3}}}{\frac {1}{\mathrm {e} ^{h\nu /kT}-1}}} $U_{\nu }(\nu ,T)=U_{\nu }^{0}(\nu ,T)={\frac {8\pi h\nu ^{3}}{c^{3}}}{\frac {1}{\mathrm {e} ^{h\nu /kT}-1}}$

U ν 0 ( ν , T ) d V d ν {\displaystyle U_{\nu }^{0}(\nu ,T)\,\mathrm {d} V\,\mathrm {d} \nu } $U_{\nu }^{0}(\nu ,T)\,\mathrm {d} V\,\mathrm {d} \nu$ ist die elektromagnetische Energie, die im Volumenelement d V {\displaystyle \mathrm {d} V} $\mathrm {d} V$ des Hohlraums im Frequenzbereich zwischen ν {\displaystyle \nu } $\nu$ und ν + d ν {\displaystyle \nu +\mathrm {d} \nu } $\nu +\mathrm {d} \nu$ vorliegt. U ν 0 ( ν , T ) {\displaystyle U_{\nu }^{0}(\nu ,T)} $U_{\nu }^{0}(\nu ,T)$ wird gemessen in der SI-Einheit J·m−3·Hz−1. In der Formel (Plancksches Strahlungsgesetz) ist h das Plancksche Wirkungsquantum, c die Lichtgeschwindigkeit im Vakuum und k die Boltzmann-Konstante.

Ebenso universell muss wegen des konstanten Umrechnungsfaktors c / 4 π {\displaystyle c/4\pi } $c/4\pi$ auch die spektrale Strahldichte der Hohlraumstrahlung sein:

L ν ( ν , T ) = L ν 0 ( ν , T ) = c 4 π U ν 0 ( ν , T ) {\displaystyle L_{\nu }(\nu ,T)=L_{\nu }^{0}(\nu ,T)={\frac {c}{4\pi }}U_{\nu }^{0}(\nu ,T)} $L_{\nu }(\nu ,T)=L_{\nu }^{0}(\nu ,T)={\frac {c}{4\pi }}U_{\nu }^{0}(\nu ,T)$ .

Ein in den Hohlraum eingebrachter Körper ändert nichts an den Eigenschaften der Hohlraumstrahlung, da diese von den Strahlungseigenschaften der neu hinzugekommenen Oberfläche und vom verringerten Hohlraumvolumen unabhängig ist. Die spektrale Bestrahlungsdichte, der der Körper ausgesetzt ist, ist gleich der spektralen Strahldichte des Strahlungsfeldes, in dem er sich befindet. Der Körper absorbiert die auf ihn treffende Strahlung vollständig. Damit im thermischen Gleichgewicht Energiedichte, Homogenität und Isotropie der Hohlraumstrahlung erhalten bleiben, muss der Körper bei jeder Frequenz und in jedem Raumwinkel ebenso viel Energie abstrahlen, wie er aus der Hohlraumstrahlung absorbiert. Die spektrale Strahldichte des Schwarzen Körpers muss daher von der Richtung unabhängig und mit der spektralen Strahldichte der Hohlraumstrahlung identisch sein.

Falls der in den Hohlraum gebrachte Körper (z. B. ein absorbierendes Gas) nicht die gesamte auftreffende Strahlung absorbiert, muss er auch weniger Strahlung emittieren, um die absorbierte Strahlung zu ersetzen. Er besitze den gerichteten spektralen Absorptionsgrad a ν ′ ( ν , β , φ , T ) {\displaystyle a_{\nu }^{\prime }(\nu ,\beta ,\varphi ,T)} $a_{\nu }^{\prime }(\nu ,\beta ,\varphi ,T)$ , das heißt, er absorbiere bei der Temperatur T {\displaystyle T} $T$ und der Frequenz ν {\displaystyle \nu } $\nu$ von der Strahlung, welche aus der durch den Polarwinkel β {\displaystyle \beta } $\beta$ und den Azimutwinkel φ {\displaystyle \varphi } $\varphi$ beschriebenen Richtung stammt, den Bruchteil a ν ′ {\displaystyle a_{\nu }^{\prime }} $a_{\nu }^{\prime }$ . Der Körper muss wiederum zur Erhaltung des thermischen Gleichgewichts bei jeder Frequenz und in jedem Raumwinkel ebenso viel Energie abstrahlen wie er aus der Hohlraumstrahlung absorbiert. Seine spektrale Strahldichte ist also

L ν K ( ν , T ) = a ν ′ L ν 0 ( ν , T ) {\displaystyle L_{\nu }^{K}(\nu ,T)=a_{\nu }^{\prime }\,L_{\nu }^{0}(\nu ,T)} $L_{\nu }^{K}(\nu ,T)=a_{\nu }^{\prime }\,L_{\nu }^{0}(\nu ,T)$ .

Dies ist das Kirchhoffsche Strahlungsgesetz: Ein beliebiger Körper der Temperatur T {\displaystyle T} $T$ strahlt bei jeder Frequenz und in jedes Raumwinkelelement ebenso viel Strahlungsleistung, wie er dort von der Strahlung eines Schwarzen Körpers absorbiert. Die Strahlungsleistung bei der Frequenz ν {\displaystyle \nu } $\nu$ ist also umso größer, je größer der Absorptionsgrad bei dieser Frequenz ist. Den größtmöglichen Absorptionsgrad a ν ′ = 1 {\displaystyle a_{\nu }^{\prime }=1} $a_{\nu }^{\prime }=1$ hat ein Schwarzer Körper, der daher auch die größtmögliche thermische Strahlungsleistung aussendet.

Da die Emission eines beliebigen Körpers nie größer als die eines Schwarzen Körpers sein kann, gilt:

L ν K ( ν , T ) = ε ν ′ L ν 0 ( ν , T ) {\displaystyle L_{\nu }^{K}(\nu ,T)=\varepsilon _{\nu }^{\prime }\,L_{\nu }^{0}(\nu ,T)} $L_{\nu }^{K}(\nu ,T)=\varepsilon _{\nu }^{\prime }\,L_{\nu }^{0}(\nu ,T)$ ,

wobei ε ν ′ {\displaystyle \varepsilon _{\nu }^{\prime }} $\varepsilon _{\nu }^{\prime }$ der gerichtete spektrale Emissionsgrad des Körpers ist ( 0 ≤ ε ν ′ ≤ 1 {\displaystyle 0\leq \varepsilon _{\nu }^{\prime }\leq 1} $0\leq \varepsilon _{\nu }^{\prime }\leq 1$ ). Vergleich mit der vorhergehenden Gleichung zeigt:

ε ν ′ = a ν ′ {\displaystyle \varepsilon _{\nu }^{\prime }=a_{\nu }^{\prime }} $\varepsilon _{\nu }^{\prime }=a_{\nu }^{\prime }$ .

„Ein guter Absorber ist auch ein guter Emitter.“

Im Hohlraum stellt sich ein Gleichgewicht der Strahlung mit dem Spektrum eines Schwarzen Strahlers ein.

Hat die Wand z. B. einen Emissionsgrad von 0,7, so absorbiert sie im thermischen Gleichgewicht 70 % der auftreffenden Hohlraumstrahlung und reflektiert den Rest. Ist nach einer Störung die spektrale Strahldichte im Hohlraum geringer als es der Hohlraumstrahlung im Gleichgewicht entspricht, so ist auch der davon absorbierte Anteil von 70 % geringer als 70 % bei idealer Hohlraumstrahlung. Die Wand emittiert aber nach wie vor aufgrund ihrer Temperatur 70 % der Strahlungsleistung, die ein Schwarzer Körper emittieren würde. Da die Wand mehr Strahlung emittiert als absorbiert, steigt die Energiedichte im Hohlraum an, bis sie den durch das Plancksche Strahlungsgesetz geforderten Wert erreicht. Somit enthält der Hohlraum im Gleichgewicht auch bei beliebigen Wänden so viel Strahlung, wie er bei Schwarzen Körpern als Wänden enthalten würde.

Im thermischen Gleichgewicht hat die von den Wänden thermisch emittierte Strahlung nach wie vor die spektralen Eigenschaften des Wandmaterials (z. B. besonders starke Emission bei bestimmten charakteristischen Wellenlängen, geringe Emission bei anderen). Die von der Wand insgesamt ausgehende Strahlung ist aber die Summe der thermischen Emission und des reflektierten Teils der aus dem Hohlraum auf die Wand treffenden Strahlung. Bei den Wellenlängen, bei denen die Wand selbst gut emittiert, absorbiert sie einen großen Anteil der auftreffenden Strahlung und reflektiert wenig; bei den Wellenlängen, bei denen die Wand selbst wenig emittiert, reflektiert sie zum Ausgleich einen großen Anteil der auftreffenden Strahlung. Die spektralen Charakteristika des Wandmaterials werden auf diese Weise ausgeglichen und die insgesamt durch Emission und Reflexion ausgesandte Strahlung hat unabhängig vom Wandmaterial ein Plancksches Spektrum.

Ein Hohlraum ist ein Speicher von elektromagnetischer Energie. Werden die Wände eines Hohlraumes auf einer einheitlichen Temperatur T {\displaystyle T} $T$ gehalten, dann kann dieser als ein thermodynamisches System im Gleichgewicht bei der Temperatur T {\displaystyle T} $T$ behandelt werden.[4][5]

Im folgenden bezeichnet V {\displaystyle V} $V$ das Volumen des Hohlraums, U {\displaystyle U} $U$ die innere Energie und p {\displaystyle p} $p$ den Druck, aus der Maxwellschen Theorie folgt für letzteren:

p ( U , V ) = U 3 V {\displaystyle p(U,V)={\frac {U}{3V}}} $p(U,V)={\frac {U}{3V}}$

und aus dem Stefan-Boltzmann-Gesetz für die innere Energie:

U ( T , V ) = b V T 4 {\displaystyle U(T,V)=bVT^{4}} $U(T,V)=bVT^{4}$

dabei ist b = 4 σ / c = 7,565 7 ⋅ 10 − 16 J m − 3 K − 4 {\displaystyle b=4\sigma /c=7{,}5657\cdot 10^{-16}\;{\text{J}}\,{\text{m}}^{-3}\,{\text{K}}^{-4}} $b=4\sigma /c=7{,}5657\cdot 10^{-16}\;{\text{J}}\,{\text{m}}^{-3}\,{\text{K}}^{-4}$ eine Konstante mit der Lichtgeschwindigkeit c {\displaystyle c} $c$ und der Stefan-Boltzmann-Konstante σ {\displaystyle \sigma } $\sigma$ .

Der Zustandsraum dieses thermodynamischen Systems ist zweidimensional; ein Zustand ist eindeutig durch Angabe der beiden extensiven Koordinaten innere Energie und Volumen ( U , V ) {\displaystyle (U,V)} $(U,V)$ bestimmt. Aufgefasst als ein Photonengas hat das System wegen der verschwindenden Ruhemasse der Photonen keine feste Teilchenzahl, sein chemisches Potential ist Null. Aus der obigen Zustandsgleichung für die innere Energie ergibt sich die Temperatur als Funktion von ( U , V ) {\displaystyle (U,V)} $(U,V)$ zu:

T ( U , V ) = ( 1 / b ) 1 4 ( U / V ) 1 4 {\displaystyle T(U,V)=(1/b)^{\frac {1}{4}}(U/V)^{\frac {1}{4}}} $T(U,V)=(1/b)^{\frac {1}{4}}(U/V)^{\frac {1}{4}}$

Mit der Eulergleichung

T S = U + p V {\displaystyle TS=U+pV} $TS=U+pV$

und den obigen Zustandsgleichungen folgt daraus die Fundamentalgleichung

S ( U , V ) = 4 3 b 1 4 U 3 4 V 1 4 {\displaystyle S(U,V)={\frac {4}{3}}b^{\frac {1}{4}}U^{\frac {3}{4}}V^{\frac {1}{4}}} $S(U,V)={\frac {4}{3}}b^{\frac {1}{4}}U^{\frac {3}{4}}V^{\frac {1}{4}}$

bzw. als Funktion der extensiven Koordinaten Entropie S {\displaystyle S} $S$ und Volumen V {\displaystyle V} $V$

U ( S , V ) = ( 3 4 S ) 4 3 ( b V ) − 1 4 {\displaystyle U(S,V)=({\frac {3}{4}}S)^{\frac {4}{3}}(bV)^{-{\frac {1}{4}}}} $U(S,V)=({\frac {3}{4}}S)^{\frac {4}{3}}(bV)^{-{\frac {1}{4}}}$

Für das Verständnis der Dynamik heißer massereicher Sterne ist die Adiabatengleichung

p V 4 3 = K o n s t a n t {\displaystyle pV^{\frac {4}{3}}=Konstant} $pV^{\frac {4}{3}}=Konstant$

mit einem Adiabatenexponenten von γ = 4 / 3 {\displaystyle \gamma =4/3} $\gamma =4/3$ von Bedeutung.[6]

Die folgende Tabelle zeigt für die Hohlraumstrahlung zu einigen Temperaturen T {\displaystyle T} $T$ die berechneten Werte der Energiedichte U / V {\displaystyle U/V} $U/V$ , des Drucks p {\displaystyle p} $p$ , der spezifischen Ausstrahlung M {\displaystyle M} $M$ und der Wellenlänge λ m a x {\displaystyle \lambda _{max}} $\lambda _{max}$ des Maximums der spektralen Energieverteilung.

T / K {\displaystyle T/\mathrm {K} } $T/\mathrm {K}$	U / V J / m 3 {\displaystyle {\frac {U/V}{\mathrm {J} /\mathrm {m} ^{3}}}} ${\frac {U/V}{\mathrm {J} /\mathrm {m} ^{3}}}$	p P a {\displaystyle {\frac {p}{\mathrm {Pa} }}} ${\frac {p}{\mathrm {Pa} }}$	M W / m 2 {\displaystyle {\frac {M}{\mathrm {W} /\mathrm {m} ^{2}}}} ${\frac {M}{\mathrm {W} /\mathrm {m} ^{2}}}$	λ m a x μ m {\displaystyle {\frac {\lambda _{max}}{\mathrm {\mu m} }}} ${\frac {\lambda _{max}}{\mathrm {\mu m} }}$
Weltraum	2.7	4.02e-14	1.34e-14	3.01e-6	1073
Zimmer (20 °C)	293	5.57e-6	1.86e-6	417	10.61
Backofen (200 °C)	473	3.78e-5	1.26e-5	2830	6.12
ca. 1000 °C	1300	2.16e-3	0.72e-3	1.62e5	2.23
Sonnenoberfläche	5772	0.839	0.280	6.29e7	0.502
Im Kern der Sonne	15.6e6	4.48e13	1.49e13	3.36e21	0.000186

Farbtemperatur nach dem planckschen Strahlungsgesetz

Die Farbtemperatur ist ein Vergleichswert, der nach dem planckschen Strahlungsgesetz und dem wienschen Verschiebungsgesetz die Intensitätskurve eines Schwarzen Körpers im Maximum beschreibt. Dieses Intensitätsmaximum verschiebt sich mit wachsender Temperatur zu kürzeren Wellenlängen.

Glühlampen mit einer Temperatur der Glühwendel von etwa 2700 bis 2800 K, wie die klassische Glühlampe, oder von 3100 bis 3200 K, wie die Halogenlampen, liegen mit dem Strahlungsmaximum im nahen Infrarot. Der spektrale Anteil im sichtbaren Bereich gibt einen gelblichen Eindruck. Der Farbeindruck der Strahlung eines thermischen Strahlers wie auch eines Schwarzen Strahlers kann zu dessen Temperaturbestimmung herangezogen werden.

Bei etwa 5500 Kelvin liegt das Intensitätsmaximum mitten im sichtbaren Bereich und entspricht etwa dem hellen Sonnenlicht am klaren Himmel. Steigt die Temperatur weiter, liegt das Intensitätsmaximum im Ultravioletten und erreicht bei weiter gesteigerten Temperaturen den Bereich der Röntgenstrahlung.

Mit zunehmender Temperatur verschiebt sich die maximale Strahlungsintensität eines Schwarzen Körpers zu kürzeren Wellenlängen, der Farbeindruck wechselt dabei vom Roten ins Bläulich-Weiße. Der Farbton einer (Wärme-)Lichtquelle lässt sich als Temperatur eines vergleichbaren Schwarzen Strahlers angeben. Damit erhält man die Farbtemperatur der Lichtquelle. Sinngemäß gilt dies dann auch für andere Selbststrahler. Vorausgesetzt ist, dass deren Eigenschaften nicht zu stark von einem Grauen Strahler abweichen.

Für den sichtbaren Bereich gilt bei hohen Temperaturen eine Näherung von Rayleigh und Jeans. Die spektrale Strahldichte, das ist die Leistung pro Flächen- und Raumwinkeleinheit und je Frequenzintervall, ist proportional zum Quadrat der Frequenz.

Eine Erhöhung der Temperatur über einen bestimmten Bereich beeinflusst nicht mehr die relative Strahlungsverteilung im Sichtbaren, der Farbeindruck bleibt „weiß“. In der CIE-Normfarbtafel endet die „Black-body-Kurve“ in einem Punkt, der in einem sehr ungesättigten violettstichigen Farbton liegt. Dieser Punkt entspricht der Farbtemperatur „unendlich“.

Die Effektivtemperatur der Sonne beträgt 5777 K.

Die Temperatur, die ein Schwarzer Körper laut Stefan-Boltzmann-Gesetz haben müsste, um dieselbe Strahlungsleistung pro Flächeneinheit zu emittieren wie ein vorgegebener Strahler heißt Effektivtemperatur dieses Strahlers. Sie weicht von der tatsächlichen Temperatur umso mehr ab, je weniger der Strahler einem Schwarzen Körper entspricht. Der Begriff der Effektivtemperatur ist daher nur bei Strahlern sinnvoll, deren Strahlungseigenschaften nicht allzu verschieden von denen eines Schwarzen Körpers sind, also bei Sternen, Glühwendeln. Bei Leuchtstofflampen, Polarlichtern und sonstigen Lichtquellen mit ausgeprägtem Linienspektrum verwendet man den Begriff Farbtemperatur.

Die Strahlung des Schwarzen Strahlers hängt nur von seiner Temperatur ab – bei jeder Frequenz und bei der betreffenden Temperatur wird die größte physikalisch mögliche thermische Strahlungsleistung abgegeben. Somit eignet sich der Schwarze Strahler als Strahlungsreferenz. Das Verhältnis der von einer beliebigen Oberfläche und der von einem Schwarzen Körper thermisch abgegebenen Strahlungsintensität ist der Emissionsgrad der Oberfläche. Der Emissionsgrad liegt stets zwischen 0 und 1 und ist in der Regel wellenlängenabhängig – es sei denn, es handelt sich um einen Grauen Strahler. Der Schwarze Körper selbst hat immer den Emissionsgrad 1 und kann daher zur Kalibrierung von Pyrometern herangezogen werden.

Ein realer Körper hat in der Regel auf verschiedenen Frequenzen und möglicherweise sogar in verschiedenen Ausstrahlrichtungen verschiedene Emissionsgrade. Für eine vollständige Charakterisierung ist der Emissionsgrad als Funktion der Frequenz und der Ausstrahlwinkel anzugeben.

Ein Lambert-Strahler ist ein Körper mit richtungsunabhängigem Emissionsgrad, er strahlt völlig diffus. Ein Grauer Körper ist ein Körper, dessen Emissionsgrad bei allen Frequenzen gleich ist. Für beide Fälle ergeben sich Vereinfachungen für Strahlungsberechnungen, so dass reale Körper – soweit möglich – näherungsweise als diffuse Strahler und Graue Körper betrachtet werden.

Nach dem kirchhoffschen Strahlungsgesetz ist für jeden Körper der gerichtete spektrale Emissionsgrad gleich dem gerichteten spektralen Absorptionsgrad. Für die anderen über die Richtungen und Frequenzen integrierten Emissions- und Absorptionsgrade gilt die Gleichheit nur unter zusätzlichen Voraussetzungen.

Die Bezeichnung „Schwarzer“ Körper kann zur irrigen Annahme führen, dass generell alle schwarz aussehenden Materialien einen hohen Absorptions- bzw. Emissionsgrad auch im infraroten Wellenlängenbereich haben. Das „Schwarz“ in „Schwarzer Körper“ bezieht sich jedoch als verallgemeinerter Begriff auf das gesamte elektromagnetische Spektrum, nicht auf einen Schwarzeindruck im Bereich des für Menschen sichtbaren Lichts. Das bedeutet konkret:

Jeder (kalte) Schwarze Körper erscheint auch tatsächlich schwarz, weil er auch im sichtbaren Wellenlängenbereich alle Strahlung absorbiert.
Nicht jeder schwarze Gegenstand ist auch ein Schwarzer Körper im Sinne des physikalischen Fachbegriffs, da er zwar im sichtbaren Wellenlängenbereich Strahlung gut, im Infraroten aber schlecht absorbieren könnte. Materialien, die diese Eigenschaft haben, werden beispielsweise zur Beschichtung von Sonnenkollektoren verwendet. Auch viele schwarze Textilien erscheinen im Nahinfrarot hell.
Ein nicht schwarzer Gegenstand könnte trotzdem im infraroten Wellenlängenbereich Strahlung gut absorbieren und emittieren, zum Beispiel weiße Farbe oder Fensterglas. Beide Stoffe besitzen im Mittleren Infrarot einen hohen Emissionsgrad.

Beispiele:

Schnee und Eis haben im Bereich des sichtbaren Lichts (400–750 nm) ein hohes Reflexionsvermögen, im nahen und fernen Infrarot erscheinen sie dagegen fast schwarz.[7]
Eine metallisch polierte Oberfläche kann durch eine aufgeklebte Klarsichtfolie im infraroten Bereich fast schwarz erscheinen.[8]
Max Planck: Ueber das Gesetz der Energieverteilung im Normalspectrum. In: Annalen der Physik. Band 309, Nr. 3, 1901, ISSN 0003-3804, S. 553–563, doi:10.1002/andp.19013090310 (kostenfreies PDF auf der Verlagsseite verfügbar).
Dieter Hoffmann: Schwarze Körper im Labor. Experimentelle Vorleistungen für Plancks Quantenhypothese. In: Physikalische Blätter. Band 56, Nr. 12, 2000, S. 43, doi:10.1002/phbl.20000561215.
Hans-Georg Schöpf: Von Kirchhoff bis Planck – Theorie der Wärmestrahlung in historisch-kritischer Darstellung. Hrsg.: Hans-Georg Schöpf (= WTB Wissenschaftliche Taschenbücher. Band 193). Akademie Verlag, Berlin 1978 (mit Auszügen aus Originalarbeiten von G. Kirchhoff, L. Boltzmann, W. Wien, Lord Rayleigh und M. Planck).
Schwarzkörperstrahlung, sehr informatives Video, ~10 min.
Was ist ein Schwarzer Körper? aus der Fernseh-Sendereihe alpha-Centauri (ca. 15 Minuten). Erstmals ausgestrahlt am 3. Sep. 2003.

↑ Peter Stephan, Stephan Kabelac, Matthias Kind, Dieter Mewes, Karlheinz Schaber, Thomas Wetzel (Hrsg.): VDI-Wärmeatlas. 12. Auflage. Springer-Verlag, Berlin 2019, ISBN 978-3-662-52988-1, Teil K1 Wärmestrahlung technischer Oberflächen, Tab. 1 Flächenspezifische Ausstrahlung des Schwarzen Körpers.
↑ a b Peter Atkins, Ronald Friedman: Molecular Quantum Mechanics. 5. Auflage. Oxford University Press, Oxford 2011, ISBN 978-0-19-954142-3, S. 1–2.
↑ B. F. Jones: A reappraisal of the use of infrared thermal image analysis in medicine. In: IEEE Transactions on Medical Imaging. Band 17, Nr. 6, Dezember 1998, S. 1019–1027, doi:10.1109/42.746635.
↑ Herbert B. Callen: Thermodynamics and an Introduction to Thermostatistics. 2. Auflage. John Wiley & Sons, New York 1985, ISBN 0-471-86256-8, 3-6 Electromagnetic Radiation, S. 78–79.
↑ Klaus Stierstadt: Thermodynamik für das Bachelor Studium. 2. vollständig überarbeitete Auflage. Springer Verlag, Heidelberg 2018, ISBN 978-3-662-55715-0, 13.2 Thermodynamik des Photonengases, S. 349–351, doi:10.1007/978-3-662-55716-7.
↑ Richard P. Feynman, Robert B.Leighton, Mattew Sands: The Feynman Lectures on Physics. 2. Auflage. Band 1. Addison Wesley, Reading Massachusetts 1966, 39-3 Compressibility of radiation, S. 39-6 (englisch, caltech.edu [abgerufen am 15. September 2024] Formel 39.18).
↑ Optische Eigenschaften von Eis und Schnee. European space Agency (ESA), 2014, abgerufen am 21. Dezember 2021.
↑ Joachim Heintze, Peter Bock (Hrsg.): Lehrbuch zur Experimentalphysik Band 2: Kontinuumsmechanik und Thermodynamik. Springer-Verlag, Berlin/Heidelberg 2016, ISBN 978-3-662-45767-2, Kapitel 7.1 Eigenschaften der Wärmestrahlung.