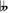7-limit tuning (original) (raw)

From Wikipedia, the free encyclopedia

Musical instrument tuning with a limit of seven

Harmonic seventh, septimal seventh

Septimal chromatic semitone on C

9/7 major third from C to E7 upside-down.[1] This, "extremely large third", may resemble a neutral third or blue note.[2]

Septimal minor third on C

7-limit or septimal tunings and intervals are musical instrument tunings that have a limit of seven: the largest prime factor contained in the interval ratios between pitches is seven. Thus, for example, 50:49 is a 7-limit interval, but 14:11 is not.

For example, the greater just minor seventh, 9:5 (Playⓘ) is a 5-limit ratio, the harmonic seventh has the ratio 7:4 and is thus a septimal interval. Similarly, the septimal chromatic semitone, 21:20, is a septimal interval as 21÷7=3. The harmonic seventh is used in the barbershop seventh chord and music. (Playⓘ) Compositions with septimal tunings include La Monte Young's The Well-Tuned Piano, Ben Johnston's String Quartet No. 4, Lou Harrison's Incidental Music for Corneille's Cinna, and Michael Harrison's Revelation: Music in Pure Intonation.

The Great Highland bagpipe is tuned to a ten-note seven-limit scale:[3] 1:1, 9:8, 5:4, 4:3, 27:20, 3:2, 5:3, 7:4, 16:9, 9:5.

In the 2nd century Ptolemy described the septimal intervals: 21/20, 7/4, 8/7, 7/6, 9/7, 12/7, 7/5, and 10/7.[4] Archytas of Tarantum is the oldest recorded musicologist to calculate 7-limit tuning systems. Those considering 7 to be consonant include Marin Mersenne,[5] Giuseppe Tartini, Leonhard Euler, François-Joseph Fétis, J. A. Serre, Moritz Hauptmann, Alexander John Ellis, Wilfred Perrett, Max Friedrich Meyer.[4] Those considering 7 to be dissonant include Gioseffo Zarlino, René Descartes, Jean-Philippe Rameau, Hermann von Helmholtz, Arthur von Oettingen, Hugo Riemann, Colin Brown, and Paul Hindemith ("chaos"[6]).[4]

Lattice and tonality diamond

[edit]

The 7-limit tonality diamond:

7/4
3/2 7/5
5/4 6/5 7/6
1/1 1/1 1/1 1/1
8/5 5/3 12/7
4/3 10/7
8/7

This diamond contains four identities (1, 3, 5, 7 [P8, P5, M3, H7]). Similarly, the 2,3,5,7 pitch lattice contains four identities and thus 3-4 axes, but a potentially infinite number of pitches. LaMonte Young created a lattice containing only identities 3 and 7, thus requiring only two axes, for The Well-Tuned Piano.

Approximation using equal temperament

[edit]

It is possible to approximate 7-limit music using equal temperament, for example 31-ET.

Fraction Cents Degree (31-ET) Name (31-ET)
1/1 0 0.0 C
8/7 231 6.0 Dhalf sharp or Edouble flat
7/6 267 6.9 D♯
6/5 316 8.2 E♭
5/4 386 10.0 E
4/3 498 12.9 F
7/5 583 15.0 F♯
10/7 617 16.0 G♭
3/2 702 18.1 G
8/5 814 21.0 A♭
5/3 884 22.8 A
12/7 933 24.1 Ahalf sharp or Bdouble flat
7/4 969 25.0 A♯
2/1 1200 31.0 C

Ptolemy's Harmonikon

[edit]

Claudius Ptolemy of Alexandria described several 7-limit tuning systems for the diatonic and chromatic genera. He describes several "soft" (μαλακός) diatonic tunings which all use 7-limit intervals.[7] One, called by Ptolemy the "tonic diatonic," is ascribed to the Pythagorean philosopher and statesman Archytas of Tarentum. It used the following tetrachord: 28:27, 8:7, 9:8. Ptolemy also shares the "soft diatonic" according to peripatetic philosopher Aristoxenus of Tarentum: 20:19, 38:35, 7:6. Ptolemy offers his own "soft diatonic" as the best alternative to Archytas and Aristoxenus, with a tetrachord of: 21:20, 10:9, 8:7.

Ptolemy also describes a "tense chromatic" tuning that utilizes the following tetrachord: 22:21, 12:11, 7:6.

  1. ^ Fonville, John. "Ben Johnston's Extended Just Intonation – A Guide for Interpreters", p. 112, Perspectives of New Music, vol. 29, no. 2 (Summer 1991), pp. 106–137.
  2. ^ Fonville (1991), p. 128.
  3. ^ Benson, Dave (2007). Music: A Mathematical Offering, p. 212. ISBN 9780521853873.
  4. ^ a b c Partch, Harry (2009). Genesis of a Music: An Account of a Creative Work, Its Roots, and Its Fulfillments, pp. 90–91. ISBN 9780786751006.
  5. ^ Shirlaw, Matthew (1900). Theory of Harmony, p. 32. ISBN 978-1-4510-1534-8.
  6. ^ Hindemith, Paul (1942). Craft of Musical Composition, vol. 1, p. 38. ISBN 0901938300.
  7. ^ Barker, Andrew (1989). Greek Musical Writings: II Harmonic and Acoustic Theory. Cambridge: Cambridge University Press. ISBN 0521616972.