Close-packing of equal spheres (original) (raw)
From Wikipedia, the free encyclopedia
Dense arrangement of congruent spheres in an infinite, regular arrangement
Illustration of the close-packing of equal spheres in both HCP (left) and FCC (right) lattices
In geometry, close-packing of equal spheres is a dense arrangement of congruent spheres in an infinite, regular arrangement (or lattice). Carl Friedrich Gauss proved that the highest average density – that is, the greatest fraction of space occupied by spheres – that can be achieved by a lattice packing is
π 3 2 ≈ 0.74048 {\displaystyle {\frac {\pi }{3{\sqrt {2}}}}\approx 0.74048} 
The same packing density can also be achieved by alternate stackings of the same close-packed planes of spheres, including structures that are aperiodic in the stacking direction. The Kepler conjecture states that this is the highest density that can be achieved by any arrangement of spheres, either regular or irregular. This conjecture was proven by T. C. Hales.[1][2] Highest density is known only for 1, 2, 3, 8, and 24 dimensions.[3]
Many crystal structures are based on a close-packing of a single kind of atom, or a close-packing of large ions with smaller ions filling the spaces between them. The cubic and hexagonal arrangements are very close to one another in energy, and it may be difficult to predict which form will be preferred from first principles.
FCC and HCP lattices
[edit]
FCC arrangement seen on 4-fold axis direction
| FCC | HCP | |
|---|---|---|
 |
 |
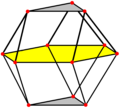 |
| The FCC arrangement can be oriented in two different planes, square or triangular. These can be seen in the cuboctahedron with 12 vertices representing the positions of 12 neighboring spheres around one central sphere. The HCP arrangement can be seen in the triangular orientation, but alternates two positions of spheres, in a triangular orthobicupola arrangement. |
There are two simple regular lattices that achieve this highest average density. They are called face-centered cubic (FCC) (also called cubic close packed) and hexagonal close-packed (HCP), based on their symmetry. Both are based upon sheets of spheres arranged at the vertices of a triangular tiling; they differ in how the sheets are stacked upon one another. The FCC lattice is also known to mathematicians as that generated by the A3 root system.[4]
Cannonballs piled on a triangular (front) and rectangular (back) base, both FCC lattices.
The problem of close-packing of spheres was first mathematically analyzed by Thomas Harriot around 1587, after a question on piling cannonballs on ships was posed to him by Sir Walter Raleigh on their expedition to America.[5]Cannonballs were usually piled in a rectangular or triangular wooden frame, forming a three-sided or four-sided pyramid. Both arrangements produce a face-centered cubic lattice – with different orientation to the ground. Hexagonal close-packing would result in a six-sided pyramid with a hexagonal base.
Collections of snowballs arranged in pyramid shape. The front pyramid is hexagonal close-packed and rear is face-centered cubic.
The cannonball problem asks which flat square arrangements of cannonballs can be stacked into a square pyramid. Édouard Lucas formulated the problem as the Diophantine equation ∑ n = 1 N n 2 = M 2 {\displaystyle \sum _{n=1}^{N}n^{2}=M^{2}} 





Positioning and spacing
[edit]
In both the FCC and HCP arrangements each sphere has twelve neighbors. For every sphere there is one gap surrounded by six spheres (octahedral) and two smaller gaps surrounded by four spheres (tetrahedral). The distances to the centers of these gaps from the centers of the surrounding spheres is √3⁄2 for the tetrahedral, and √2 for the octahedral, when the sphere radius is 1.
Relative to a reference layer with positioning A, two more positionings B and C are possible. Every sequence of A, B, and C without immediate repetition of the same one is possible and gives an equally dense packing for spheres of a given radius.
The most regular ones are
- FCC = ABC ABC ABC... (every third layer is the same)
- HCP = AB AB AB AB... (every other layer is the same).
There is an uncountably infinite number of disordered arrangements of planes (e.g. ABCACBABABAC...) that are sometimes collectively referred to as "Barlow packings", after crystallographer William Barlow.[6]
In close-packing, the center-to-center spacing of spheres in the xy plane is a simple honeycomb-like tessellation with a pitch (distance between sphere centers) of one sphere diameter. The distance between sphere centers, projected on the z (vertical) axis, is:
pitch Z = 6 ⋅ d 3 ≈ 0.816 496 58 d , {\displaystyle {\text{pitch}}_{Z}={\sqrt {6}}\cdot {d \over 3}\approx 0.816\,496\,58d,}
where d is the diameter of a sphere; this follows from the tetrahedral arrangement of close-packed spheres.
The coordination number of HCP and FCC is 12 and their atomic packing factors (APFs) are equal to the number mentioned above, 0.74.
| Comparison between HCP and FCC |
|---|
 |
| Figure 1 – The HCP lattice (left) and the FCC lattice (right). The outline of each respective Bravais lattice is shown in red. The letters indicate which layers are the same. There are two "A" layers in the HCP matrix, where all the spheres are in the same position. All three layers in the FCC stack are different. Note the FCC stacking may be converted to the HCP stacking by translation of the upper-most sphere, as shown by the dashed outline. |
Figure 2 Thomas Harriot in ca. 1585 first pondered the mathematics of the cannonball arrangement or cannonball stack, which has an FCC lattice. Note how the two balls facing the viewer in the second tier from the top contact the same ball in the tier below. This does not occur in an HCP lattice (the left organization in Figure 1 above, and Figure 4 below).
Figure 3 Shown here is a modified form of the cannonball stack wherein three extra spheres have been added to show all eight spheres in the top three tiers of the FCC lattice diagramed in Figure 1.
Figure 4 Shown here are all eleven spheres of the HCP lattice illustrated in Figure 1. The difference between this stack and the top three tiers of the cannonball stack all occurs in the bottom tier, which is rotated half the pitch diameter of a sphere (60°). Note how the two balls facing the viewer in the second tier from the top do not contact the same ball in the tier below.
Figure 5 This animated view helps illustrate the three-sided pyramidal (tetrahedral) shape of the cannonball arrangement.
When forming any sphere-packing lattice, the first fact to notice is that whenever two spheres touch a straight line may be drawn from the center of one sphere to the center of the other intersecting the point of contact. The distance between the centers along the shortest path namely that straight line will therefore be _r_1 + _r_2 where _r_1 is the radius of the first sphere and r_2 is the radius of the second. In close packing all of the spheres share a common radius, r. Therefore, two centers would simply have a distance 2_r.
An animation of close-packing lattice generation. Note: If a third layer (not shown) is directly over the first layer, then the HCP lattice is built. If the third layer is placed over holes in the first layer, then the FCC lattice is created.
To form an A-B-A-B-... hexagonal close packing of spheres, the coordinate points of the lattice will be the spheres' centers. Suppose, the goal is to fill a box with spheres according to HCP. The box would be placed on the _x_-_y_-z coordinate space.
First form a row of spheres. The centers will all lie on a straight line. Their x_-coordinate will vary by 2_r since the distance between each center of the spheres are touching is 2_r_. The y_-coordinate and z-coordinate will be the same. For simplicity, say that the balls are the first row and that their y_- and z_-coordinates are simply r, so that their surfaces rest on the zero-planes. Coordinates of the centers of the first row will look like (2_r, r, r), (4_r, r, r), (6_r ,r, r), (8_r_ ,r, r), ... .
Now, form the next row of spheres. Again, the centers will all lie on a straight line with x_-coordinate differences of 2_r, but there will be a shift of distance r in the _x_-direction so that the center of every sphere in this row aligns with the x_-coordinate of where two spheres touch in the first row. This allows the spheres of the new row to slide in closer to the first row until all spheres in the new row are touching two spheres of the first row. Since the new spheres touch two spheres, their centers form an equilateral triangle with those two neighbors' centers. The side lengths are all 2_r, so the height or y_-coordinate difference between the rows is √3_r. Thus, this row will have coordinates like this:
( r , r + 3 r , r ) , ( 3 r , r + 3 r , r ) , ( 5 r , r + 3 r , r ) , ( 7 r , r + 3 r , r ) , … . {\displaystyle \left(r,r+{\sqrt {3}}r,r\right),\ \left(3r,r+{\sqrt {3}}r,r\right),\ \left(5r,r+{\sqrt {3}}r,r\right),\ \left(7r,r+{\sqrt {3}}r,r\right),\dots .}
The first sphere of this row only touches one sphere in the original row, but its location follows suit with the rest of the row.
The next row follows this pattern of shifting the _x_-coordinate by r and the _y_-coordinate by √3. Add rows until reaching the x and y maximum borders of the box.
In an A-B-A-B-... stacking pattern, the odd numbered planes of spheres will have exactly the same coordinates save for a pitch difference in the _z_-coordinates and the even numbered planes of spheres will share the same _x_- and _y_-coordinates. Both types of planes are formed using the pattern mentioned above, but the starting place for the first row's first sphere will be different.
Using the plane described precisely above as plane #1, the A plane, place a sphere on top of this plane so that it lies touching three spheres in the A-plane. The three spheres are all already touching each other, forming an equilateral triangle, and since they all touch the new sphere, the four centers form a regular tetrahedron.[7] All of the sides are equal to 2_r_ because all of the sides are formed by two spheres touching. The height of which or the _z_-coordinate difference between the two "planes" is √6_r_2/3. This, combined with the offsets in the x and _y_-coordinates gives the centers of the first row in the B plane:
( r , r + 3 r 3 , r + 6 r 2 3 ) , ( 3 r , r + 3 r 3 , r + 6 r 2 3 ) , ( 5 r , r + 3 r 3 , r + 6 r 2 3 ) , ( 7 r , r + 3 r 3 , r + 6 r 2 3 ) , … . {\displaystyle \left(r,r+{\frac {{\sqrt {3}}r}{3}},r+{\frac {{\sqrt {6}}r2}{3}}\right),\ \left(3r,r+{\frac {{\sqrt {3}}r}{3}},r+{\frac {{\sqrt {6}}r2}{3}}\right),\ \left(5r,r+{\frac {{\sqrt {3}}r}{3}},r+{\frac {{\sqrt {6}}r2}{3}}\right),\ \left(7r,r+{\frac {{\sqrt {3}}r}{3}},r+{\frac {{\sqrt {6}}r2}{3}}\right),\dots .}
The second row's coordinates follow the pattern first described above and are:
( 2 r , r + 4 3 r 3 , r + 6 r 2 3 ) , ( 4 r , r + 4 3 r 3 , r + 6 r 2 3 ) , ( 6 r , r + 4 3 r 3 , r + 6 r 2 3 ) , ( 8 r , r + 4 3 r 3 , r + 6 r 2 3 ) , … . {\displaystyle \left(2r,r+{\frac {4{\sqrt {3}}r}{3}},r+{\frac {{\sqrt {6}}r2}{3}}\right),\ \left(4r,r+{\frac {4{\sqrt {3}}r}{3}},r+{\frac {{\sqrt {6}}r2}{3}}\right),\ \left(6r,r+{\frac {4{\sqrt {3}}r}{3}},r+{\frac {{\sqrt {6}}r2}{3}}\right),\ \left(8r,r+{\frac {4{\sqrt {3}}r}{3}},r+{\frac {{\sqrt {6}}r2}{3}}\right),\dots .}
The difference to the next plane, the A plane, is again √6_r_2/3 in the _z_-direction and a shift in the x and y to match those _x_- and _y_-coordinates of the first A plane.[8]
In general, the coordinates of sphere centers can be written as:
[ 2 i + ( ( j + k ) mod 2 ) 3 [ j + 1 3 ( k mod 2 ) ] 2 6 3 k ] r {\displaystyle {\begin{bmatrix}2i+((j\ +\ k){\bmod {2}})\\{\sqrt {3}}\left[j+{\frac {1}{3}}(k{\bmod {2}})\right]\\{\frac {2{\sqrt {6}}}{3}}k\end{bmatrix}}r}
where i, j and k are indices starting at 0 for the _x_-, _y_- and _z_-coordinates.
Miller–Bravais index for HCP lattice
Crystallographic features of HCP systems, such as vectors and atomic plane families, can be described using a four-value Miller index notation ( hkil ) in which the third index i denotes a degenerate but convenient component which is equal to −h − k. The h, i and k index directions are separated by 120°, and are thus not orthogonal; the l component is mutually perpendicular to the h, i and k index directions.
Filling the remaining space
[edit]
The FCC and HCP packings are the densest known packings of equal spheres with the highest symmetry (smallest repeat units). Denser sphere packings are known, but they involve unequal sphere packing. A packing density of 1, filling space completely, requires non-spherical shapes, such as honeycombs.
Replacing each contact point between two spheres with an edge connecting the centers of the touching spheres produces tetrahedrons and octahedrons of equal edge lengths. The FCC arrangement produces the tetrahedral-octahedral honeycomb. The HCP arrangement produces the gyrated tetrahedral-octahedral honeycomb. If, instead, every sphere is augmented with the points in space that are closer to it than to any other sphere, the duals of these honeycombs are produced: the rhombic dodecahedral honeycomb for FCC, and the trapezo-rhombic dodecahedral honeycomb for HCP.
Spherical bubbles appear in soapy water in a FCC or HCP arrangement when the water in the gaps between the bubbles drains out. This pattern also approaches the rhombic dodecahedral honeycomb or trapezo-rhombic dodecahedral honeycomb. However, such FCC or HCP foams of very small liquid content are unstable, as they do not satisfy Plateau's laws. The Kelvin foam and the Weaire–Phelan foam are more stable, having smaller interfacial energy in the limit of a very small liquid content.[9]
There are two types of interstitial holes left by hcp and fcc conformations; tetrahedral and octahedral void. Four spheres surround the tetrahedral hole with three spheres being in one layer and one sphere from the next layer. Six spheres surround an octahedral voids with three spheres coming from one layer and three spheres coming from the next layer. Structures of many simple chemical compounds, for instance, are often described in terms of small atoms occupying tetrahedral or octahedral holes in closed-packed systems that are formed from larger atoms.
Layered structures are formed by alternating empty and filled octahedral planes. Two octahedral layers usually allow for four structural arrangements that can either be filled by an hpc of fcc packing systems. In filling tetrahedral holes a complete filling leads to fcc field array. In unit cells, hole filling can sometimes lead to polyhedral arrays with a mix of hcp and fcc layering.[10]
- ^ Hales, T. C. (1998). "An overview of the Kepler conjecture". arXiv:math/9811071v2.
- ^ Szpiro, George (2003). "Mathematics: Does the proof stack up?". Nature. 424 (6944): 12–13. Bibcode:2003Natur.424...12S. doi:10.1038/424012a. PMID 12840727.
- ^ Cohn, H.; Kumar, A.; Miller, S. D.; Radchenko, D.; Viazovska, M. (2017). "The sphere packing problem in dimension 24". Annals of Mathematics. 185 (3): 1017–1033. arXiv:1603.06518. doi:10.4007/annals.2017.185.3.8. S2CID 119281758.
- ^ Conway, John Horton; Sloane, Neil James Alexander; Bannai, Eiichi (1999). Sphere packings, lattices, and groups. Springer. Section 6.3. ISBN 9780387985855.
- ^ Darling, David. "Cannonball Problem". The Internet Encyclopedia of Science.
- ^ Barlow, William (1883). "Probable Nature of the Internal Symmetry of Crystals". Nature. 29 (738): 186–188. Bibcode:1883Natur..29..186B. doi:10.1038/029186a0.
- ^ "on Sphere Packing". Grunch.net. Retrieved 2014-06-12.
- ^ Weisstein, Eric W. "Hexagonal Close Packing". MathWorld.
- ^ Cantat, Isabelle; Cohen-Addad, Sylvie; Elias, Florence; Graner, François; Höhler, Reinhard; Flatman, Ruth; Pitois, Olivier (2013). Foams, Structure and Dynamics. Oxford: Oxford University Press. ISBN 9780199662890.
- ^ Woodward, Patrick M.; Karen, Pavel; Evans, John S. O.; Vogt, Thomas (2021). Solid State Materials Chemistry. Cambridge: Cambridge University Press. ISBN 9780521873253.













![{\displaystyle {\begin{bmatrix}2i+((j\ +\ k){\bmod {2}})\\{\sqrt {3}}\left[j+{\frac {1}{3}}(k{\bmod {2}})\right]\\{\frac {2{\sqrt {6}}}{3}}k\end{bmatrix}}r}](https://wikimedia.org/api/rest_v1/media/math/render/svg/89bb83425e28ac94a674a3f1b10f04541208ef7a)
