Convex combination (original) (raw)
From Wikipedia, the free encyclopedia
Linear combination of points where all coefficients are non-negative and sum to 1
Given three points x 1 , x 2 , x 3 {\displaystyle x_{1},x_{2},x_{3}} 



Convex combination of two points v 1 , v 2 ∈ R 2 {\displaystyle v_{1},v_{2}\in \mathbb {R} ^{2}} 

![{\displaystyle t\in [0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/31a5c18739ff04858eecc8fec2f53912c348e0e5)

Convex combination of three points v 0 , v 1 , v 2 of 2 -simplex ∈ R 2 {\displaystyle v_{0},v_{1},v_{2}{\text{ of }}2{\text{-simplex}}\in \mathbb {R} ^{2}} 






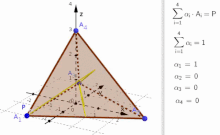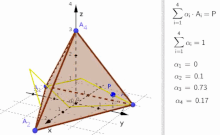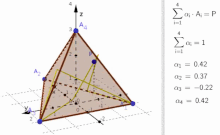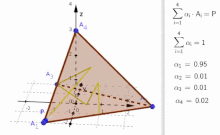
Convex combination of four points A 1 , A 2 , A 3 , A 4 ∈ R 3 {\displaystyle A_{1},A_{2},A_{3},A_{4}\in \mathbb {R} ^{3}} 





Convex combination of two functions as vectors in a vector space of functions - visualized in Open Source Geogebra with [ a , b ] = [ − 4 , 7 ] {\displaystyle [a,b]=[-4,7]} ![{\displaystyle [a,b]=[-4,7]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/183bacef4a989104893e2c37017d84af54a1a23f)
![{\displaystyle f:[a,b]\to \mathbb {R} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/b592d102ccd1ba134d401c5b3ea177baaba3ffac)

![{\displaystyle g:[a,b]\to \mathbb {R} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/8b1d5103d0e36767a27715bcfc57137119294aad)




In convex geometry and vector algebra, a convex combination is a linear combination of points (which can be vectors, scalars, or more generally points in an affine space) where all coefficients are non-negative and sum to 1.[1] In other words, the operation is equivalent to a standard weighted average, but whose weights are expressed as a percent of the total weight, instead of as a fraction of the count of the weights as in a standard weighted average.
More formally, given a finite number of points x 1 , x 2 , … , x n {\displaystyle x_{1},x_{2},\dots ,x_{n}} 
α 1 x 1 + α 2 x 2 + ⋯ + α n x n {\displaystyle \alpha _{1}x_{1}+\alpha _{2}x_{2}+\cdots +\alpha _{n}x_{n}}
where the real numbers α i {\displaystyle \alpha _{i}} 


As a particular example, every convex combination of two points lies on the line segment between the points.[1]
A set is convex if it contains all convex combinations of its points. The convex hull of a given set of points is identical to the set of all their convex combinations.[1]
There exist subsets of a vector space that are not closed under linear combinations but are closed under convex combinations. For example, the interval [ 0 , 1 ] {\displaystyle [0,1]} ![{\displaystyle [0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/738f7d23bb2d9642bab520020873cccbef49768d)
- ^ a b c d Rockafellar, R. Tyrrell (1970), Convex Analysis, Princeton Mathematical Series, vol. 28, Princeton University Press, Princeton, N.J., pp. 11–12, MR 0274683
- Convex sum/combination with a triangle - interactive illustration
- Convex sum/combination with a hexagon - interactive illustration
- Convex sum/combination with a tetraeder - interactive illustration