Cross-polytope (original) (raw)
From Wikipedia, the free encyclopedia
Regular polytope dual to the hypercube in any number of dimensions
Cross-polytopes of dimension 2 to 5
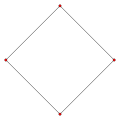 |
 |
|---|---|
| 2 dimensionssquare | 3 dimensionsoctahedron |
 |
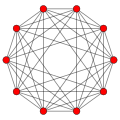 |
| 4 dimensions16-cell | 5 dimensions5-orthoplex |
In geometry, a cross-polytope,[1] hyperoctahedron, orthoplex,[2] staurotope,[3] or cocube is a regular, convex polytope that exists in _n_-dimensional Euclidean space. A 2-dimensional cross-polytope is a square, a 3-dimensional cross-polytope is a regular octahedron, and a 4-dimensional cross-polytope is a 16-cell. Its facets are simplexes of the previous dimension, while the cross-polytope's vertex figure is another cross-polytope from the previous dimension.
The vertices of a cross-polytope can be chosen as the unit vectors pointing along each co-ordinate axis – i.e. all the permutations of (±1, 0, 0, ..., 0). The cross-polytope is the convex hull of its vertices. The _n_-dimensional cross-polytope can also be defined as the closed unit ball (or, according to some authors, its boundary) in the ℓ1-norm on Rn:
{ x ∈ R n : ‖ x ‖ 1 ≤ 1 } . {\displaystyle \{x\in \mathbb {R} ^{n}:\|x\|_{1}\leq 1\}.}
In 1 dimension the cross-polytope is simply the line segment [−1, +1], in 2 dimensions it is a square (or diamond) with vertices {(±1, 0), (0, ±1)}. In 3 dimensions it is an octahedron—one of the five convex regular polyhedra known as the Platonic solids. This can be generalised to higher dimensions with an _n_-orthoplex being constructed as a bipyramid with an (_n_−1)-orthoplex base.
The cross-polytope is the dual polytope of the hypercube. The 1-skeleton of an n_-dimensional cross-polytope is the Turán graph T(2_n, n) (also known as a cocktail party graph [4]).
The 4-dimensional cross-polytope also goes by the name hexadecachoron or 16-cell. It is one of the six convex regular 4-polytopes. These 4-polytopes were first described by the Swiss mathematician Ludwig Schläfli in the mid-19th century.
The cross-polytope family is one of three regular polytope families, labeled by Coxeter as βn, the other two being the hypercube family, labeled as γn, and the simplex family, labeled as αn. A fourth family, the infinite tessellations of hypercubes, he labeled as δn.[5]
The n_-dimensional cross-polytope has 2_n vertices, and 2_n_ facets ((n − 1)-dimensional components) all of which are (n − 1)-simplices. The vertex figures are all (n − 1)-cross-polytopes. The Schläfli symbol of the cross-polytope is {3,3,...,3,4}.
The dihedral angle of the _n_-dimensional cross-polytope is δ n = arccos ( 2 − n n ) {\displaystyle \delta _{n}=\arccos \left({\frac {2-n}{n}}\right)} 
The hypervolume of the _n_-dimensional cross-polytope is
2 n n ! . {\displaystyle {\frac {2^{n}}{n!}}.}
For each pair of non-opposite vertices, there is an edge joining them. More generally, each set of k + 1 orthogonal vertices corresponds to a distinct _k_-dimensional component which contains them. The number of _k_-dimensional components (vertices, edges, faces, ..., facets) in an _n_-dimensional cross-polytope is thus given by (see binomial coefficient):
2 k + 1 ( n k + 1 ) {\displaystyle 2^{k+1}{n \choose {k+1}}} 
The extended f-vector for an _n_-orthoplex can be computed by (1,2)n, like the coefficients of polynomial products. For example a 16-cell is (1,2)4 = (1,4,4)2 = (1,8,24,32,16).
There are many possible orthographic projections that can show the cross-polytopes as 2-dimensional graphs. Petrie polygon projections map the points into a regular 2_n_-gon or lower order regular polygons. A second projection takes the 2(_n_−1)-gon petrie polygon of the lower dimension, seen as a bipyramid, projected down the axis, with 2 vertices mapped into the center.
Cross-polytope elements
| n | β_n_ _k_11 | Name(s)Graph | Graph2_n_-gon | Schläfli | Coxeter-Dynkin diagrams | Vertices | Edges | Faces | Cells | 4-faces | 5-faces | 6-faces | 7-faces | 8-faces | 9-faces | 10-faces |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | β0 | Point0-orthoplex | . | ( ) |  |
1 | ||||||||||
| 1 | β1 | Line segment1-orthoplex |  |
{ } |   |
2 | 1 | |||||||||
| 2 | β2 −111 | Square2-orthoplexBicross |  |
{4}2{ } = { }+{ } |       |
4 | 4 | 1 | ||||||||
| 3 | β3011 | Octahedron3-orthoplexTricross |  |
{3,4}{31,1}3{ } |              |
6 | 12 | 8 | 1 | |||||||
| 4 | β4111 | 16-cell4-orthoplexTetracross |  |
{3,3,4}{3,31,1}4{ } |                    |
8 | 24 | 32 | 16 | 1 | ||||||
| 5 | β5211 | 5-orthoplexPentacross |  |
{33,4}{3,3,31,1}5{ } |                          |
10 | 40 | 80 | 80 | 32 | 1 | |||||
| 6 | β6311 | 6-orthoplexHexacross |  |
{34,4}{33,31,1}6{ } |                                |
12 | 60 | 160 | 240 | 192 | 64 | 1 | ||||
| 7 | β7411 | 7-orthoplexHeptacross |  |
{35,4}{34,31,1}7{ } |                                      |
14 | 84 | 280 | 560 | 672 | 448 | 128 | 1 | |||
| 8 | β8511 | 8-orthoplexOctacross |  |
{36,4}{35,31,1}8{ } |                                            |
16 | 112 | 448 | 1120 | 1792 | 1792 | 1024 | 256 | 1 | ||
| 9 | β9611 | 9-orthoplexEnneacross |  |
{37,4}{36,31,1}9{ } |                                                  |
18 | 144 | 672 | 2016 | 4032 | 5376 | 4608 | 2304 | 512 | 1 | |
| 10 | β10711 | 10-orthoplexDecacross |  |
{38,4}{37,31,1}10{ } |                                                        |
20 | 180 | 960 | 3360 | 8064 | 13440 | 15360 | 11520 | 5120 | 1024 | 1 |
| ... | ||||||||||||||||
| n | β_n_ _k_11 | _n_-orthoplex_n_-cross | {3_n_ − 2,4}{3_n_ − 3,31,1}n{} |      ... ...          ... ...             ... ...  |
2_n_ 0-faces, ... 2 k + 1 ( n k + 1 ) {\displaystyle 2^{k+1}{n \choose k+1}}  _k_-faces ..., 2_n_ (_n_−1)-faces _k_-faces ..., 2_n_ (_n_−1)-faces |
The vertices of an axis-aligned cross polytope are all at equal distance from each other in the Manhattan distance (L1 norm). Kusner's conjecture states that this set of 2_d_ points is the largest possible equidistant set for this distance.[7]
Generalized orthoplex
[edit]
Regular complex polytopes can be defined in complex Hilbert space called generalized orthoplexes (or cross polytopes), β_p_
n = 2{3}2{3}...2{4}p, or 


 ..
..


 . Real solutions exist with p = 2, i.e. β2
. Real solutions exist with p = 2, i.e. β2
n = β_n_ = 2{3}2{3}...2{4}2 = {3,3,..,4}. For p > 2, they exist in C n {\displaystyle \mathbb {\mathbb {C} } ^{n}} 
2 make K_p,p for complete bipartite graph, β_p_
3 make K_p_,p,p for complete tripartite graphs. β_p_
n creates K_p_ n. An orthogonal projection can be defined that maps all the vertices equally-spaced on a circle, with all pairs of vertices connected, except multiples of n. The regular polygon perimeter in these orthogonal projections is called a petrie polygon.
Generalized orthoplexes
| p = 2 | p = 3 | p = 4 | p = 5 | p = 6 | p = 7 | p = 8 | ||
|---|---|---|---|---|---|---|---|---|
R 2 {\displaystyle \mathbb {R} ^{2}}  |
 2{4}2 = {4} = 2{4}2 = {4} =    K2,2 K2,2 |
C 2 {\displaystyle \mathbb {\mathbb {C} } ^{2}}  |
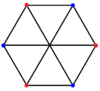 2{4}3 = 2{4}3 =    K3,3 K3,3 |
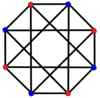 2{4}4 = 2{4}4 =    K4,4 K4,4 |
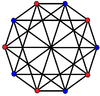 2{4}5 = 2{4}5 =    K5,5 K5,5 |
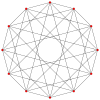 2{4}6 = 2{4}6 =    K6,6 K6,6 |
 2{4}7 = 2{4}7 =    K7,7 K7,7 |
 2{4}8 = 2{4}8 =    K8,8 K8,8 |
R 3 {\displaystyle \mathbb {R} ^{3}}  |
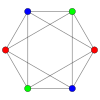 2{3}2{4}2 = {3,4} = 2{3}2{4}2 = {3,4} =      K2,2,2 K2,2,2 |
C 3 {\displaystyle \mathbb {\mathbb {C} } ^{3}}  |
 2{3}2{4}3 = 2{3}2{4}3 =      K3,3,3 K3,3,3 |
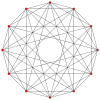 2{3}2{4}4 = 2{3}2{4}4 =      K4,4,4 K4,4,4 |
 2{3}2{4}5 = 2{3}2{4}5 =      K5,5,5 K5,5,5 |
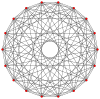 2{3}2{4}6 = 2{3}2{4}6 =      K6,6,6 K6,6,6 |
 2{3}2{4}7 = 2{3}2{4}7 =      K7,7,7 K7,7,7 |
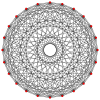 2{3}2{4}8 = 2{3}2{4}8 =      K8,8,8 K8,8,8 |
R 4 {\displaystyle \mathbb {R} ^{4}}  |
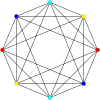 2{3}2{3}2{3,3,4} = 2{3}2{3}2{3,3,4} =        K2,2,2,2 K2,2,2,2 |
C 4 {\displaystyle \mathbb {\mathbb {C} } ^{4}}  |
 2{3}2{3}2{4}3 2{3}2{3}2{4}3       K3,3,3,3 K3,3,3,3 |
 2{3}2{3}2{4}4 2{3}2{3}2{4}4       K4,4,4,4 K4,4,4,4 |
 2{3}2{3}2{4}5 2{3}2{3}2{4}5       K5,5,5,5 K5,5,5,5 |
 2{3}2{3}2{4}6 2{3}2{3}2{4}6       K6,6,6,6 K6,6,6,6 |
 2{3}2{3}2{4}7 2{3}2{3}2{4}7       K7,7,7,7 K7,7,7,7 |
 2{3}2{3}2{4}8 2{3}2{3}2{4}8       K8,8,8,8 K8,8,8,8 |
R 5 {\displaystyle \mathbb {R} ^{5}}  |
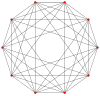 2{3}2{3}2{3}2{4}2{3,3,3,4} = 2{3}2{3}2{3}2{4}2{3,3,3,4} =          K2,2,2,2,2 K2,2,2,2,2 |
C 5 {\displaystyle \mathbb {\mathbb {C} } ^{5}}  |
 2{3}2{3}2{3}2{4}3 2{3}2{3}2{3}2{4}3         K3,3,3,3,3 K3,3,3,3,3 |
 2{3}2{3}2{3}2{4}4 2{3}2{3}2{3}2{4}4         K4,4,4,4,4 K4,4,4,4,4 |
 2{3}2{3}2{3}2{4}5 2{3}2{3}2{3}2{4}5         K5,5,5,5,5 K5,5,5,5,5 |
 2{3}2{3}2{3}2{4}6 2{3}2{3}2{3}2{4}6         K6,6,6,6,6 K6,6,6,6,6 |
 2{3}2{3}2{3}2{4}7 2{3}2{3}2{3}2{4}7         K7,7,7,7,7 K7,7,7,7,7 |
 2{3}2{3}2{3}2{4}8 2{3}2{3}2{3}2{4}8         K8,8,8,8,8 K8,8,8,8,8 |
R 6 {\displaystyle \mathbb {R} ^{6}}  |
 2{3}2{3}2{3}2{3}2{4}2{3,3,3,3,4} = 2{3}2{3}2{3}2{3}2{4}2{3,3,3,3,4} =            K2,2,2,2,2,2 K2,2,2,2,2,2 |
C 6 {\displaystyle \mathbb {\mathbb {C} } ^{6}}  |
 2{3}2{3}2{3}2{3}2{4}3 2{3}2{3}2{3}2{3}2{4}3           K3,3,3,3,3,3 K3,3,3,3,3,3 |
 2{3}2{3}2{3}2{3}2{4}4 2{3}2{3}2{3}2{3}2{4}4           K4,4,4,4,4,4 K4,4,4,4,4,4 |
 2{3}2{3}2{3}2{3}2{4}5 2{3}2{3}2{3}2{3}2{4}5           K5,5,5,5,5,5 K5,5,5,5,5,5 |
 2{3}2{3}2{3}2{3}2{4}6 2{3}2{3}2{3}2{3}2{4}6           K6,6,6,6,6,6 K6,6,6,6,6,6 |
 2{3}2{3}2{3}2{3}2{4}7 2{3}2{3}2{3}2{3}2{4}7           K7,7,7,7,7,7 K7,7,7,7,7,7 |
 2{3}2{3}2{3}2{3}2{4}8 2{3}2{3}2{3}2{3}2{4}8           K8,8,8,8,8,8 K8,8,8,8,8,8 |
Cross-polytopes can be combined with their dual cubes to form compound polytopes:
- In two dimensions, we obtain the octagrammic star figure {8/2},
- In three dimensions we obtain the compound of cube and octahedron,
- In four dimensions we obtain the compound of tesseract and 16-cell.
- List of regular polytopes
- Hyperoctahedral group, the symmetry group of the cross-polytope
- ^ Coxeter 1973, pp. 121–122, §7.21. illustration Fig 7-2B.
- ^ Conway, J. H.; Sloane, N. J. A. (1991). "The Cell Structures of Certain Lattices". In Hilton, P.; Hirzebruch, F.; Remmert, R. (eds.). Miscellanea Mathematica. Berlin: Springer. pp. 89–90. doi:10.1007/978-3-642-76709-8_5. ISBN 978-3-642-76711-1.
- ^ McMullen, Peter (2020). Geometric Regular Polytopes. Cambridge University Press. p. 92. ISBN 978-1-108-48958-4.
- ^ Weisstein, Eric W. "Cocktail Party Graph". MathWorld.
- ^ Coxeter 1973, pp. 120–124, §7.2.
- ^ Coxeter 1973, p. 121, §7.2.2..
- ^ Guy, Richard K. (1983), "An olla-podrida of open problems, often oddly posed", American Mathematical Monthly, 90 (3): 196–200, doi:10.2307/2975549, JSTOR 2975549.
- ^ Coxeter, Regular Complex Polytopes, p. 108
- Coxeter, H.S.M. (1973). Regular Polytopes (3rd ed.). New York: Dover.
- pp. 121-122, §7.21. see illustration Fig 7.2B
- p. 296, Table I (iii): Regular Polytopes, three regular polytopes in n-dimensions (n≥5)
- Weisstein, Eric W. "Cross polytope". MathWorld.
| vteFundamental convex regular and uniform polytopes in dimensions 2–10 | |||||
|---|---|---|---|---|---|
| Family | A n | B n | _I_2(p) / D n | _E_6 / _E_7 / _E_8 / _F_4 / _G_2 | Hn |
| Regular polygon | Triangle | Square | p-gon | Hexagon | Pentagon |
| Uniform polyhedron | Tetrahedron | Octahedron • Cube | Demicube | Dodecahedron • Icosahedron | |
| Uniform polychoron | Pentachoron | 16-cell • Tesseract | Demitesseract | 24-cell | 120-cell • 600-cell |
| Uniform 5-polytope | 5-simplex | 5-orthoplex • 5-cube | 5-demicube | ||
| Uniform 6-polytope | 6-simplex | 6-orthoplex • 6-cube | 6-demicube | 122 • 221 | |
| Uniform 7-polytope | 7-simplex | 7-orthoplex • 7-cube | 7-demicube | 132 • 231 • 321 | |
| Uniform 8-polytope | 8-simplex | 8-orthoplex • 8-cube | 8-demicube | 142 • 241 • 421 | |
| Uniform 9-polytope | 9-simplex | 9-orthoplex • 9-cube | 9-demicube | ||
| Uniform 10-polytope | 10-simplex | 10-orthoplex • 10-cube | 10-demicube | ||
| Uniform _n_-polytope | _n_-simplex | _n_-orthoplex • _n_-cube | _n_-demicube | 1k2 • 2k1 • k21 | _n_-pentagonal polytope |
| Topics: Polytope families • Regular polytope • List of regular polytopes and compounds |

