Extremum estimator (original) (raw)
From Wikipedia, the free encyclopedia
In statistics and econometrics, extremum estimators are a wide class of estimators for parametric models that are calculated through maximization (or minimization) of a certain objective function, which depends on the data. The general theory of extremum estimators was developed by Amemiya (1985).
An estimator θ ^ {\displaystyle \scriptstyle {\hat {\theta }}} 

θ ^ = a r g m a x θ ∈ Θ Q ^ n ( θ ) , {\displaystyle {\hat {\theta }}={\underset {\theta \in \Theta }{\operatorname {arg\;max} }}\ {\widehat {Q}}_{n}(\theta ),}
where Θ is the parameter space. Sometimes a slightly weaker definition is given:
Q ^ n ( θ ^ ) ≥ max θ ∈ Θ Q ^ n ( θ ) − o p ( 1 ) , {\displaystyle {\widehat {Q}}_{n}({\hat {\theta }})\geq \max _{\theta \in \Theta }\,{\widehat {Q}}_{n}(\theta )-o_{p}(1),}
where o p(1) is the variable converging in probability to zero. With this modification θ ^ {\displaystyle \scriptstyle {\hat {\theta }}} 
The theory of extremum estimators does not specify what the objective function should be. There are various types of objective functions suitable for different models, and this framework allows us to analyse the theoretical properties of such estimators from a unified perspective. The theory only specifies the properties that the objective function has to possess, and so selecting a particular objective function only requires verifying that those properties are satisfied.
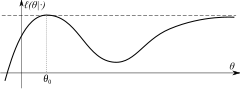
When the parameter space Θ is not compact (Θ = R in this example), then even if the objective function is uniquely maximized at _θ_0, this maximum may be not well-separated, in which case the estimator θ ^ {\displaystyle \scriptscriptstyle {\hat {\theta }}} 
If the parameter space Θ is compact and there is a limiting function _Q_0(θ) such that: Q ^ n ( θ ) {\displaystyle \scriptstyle {\hat {Q}}_{n}(\theta )} 

The uniform convergence in probability of Q ^ n ( θ ) {\displaystyle \scriptstyle {\hat {Q}}_{n}(\theta )} 
sup θ ∈ Θ | Q ^ n ( θ ) − Q 0 ( θ ) | → p 0. {\displaystyle \sup _{\theta \in \Theta }{\big |}{\hat {Q}}_{n}(\theta )-Q_{0}(\theta ){\big |}\ {\xrightarrow {p}}\ 0.}
The requirement for Θ to be compact can be replaced with a weaker assumption that the maximum of _Q_0 was well-separated, that is there should not exist any points θ that are distant from _θ_0 but such that _Q_0(θ) were close to _Q_0(_θ_0). Formally, it means that for any sequence {θi} such that _Q_0(θi) → _Q_0(_θ_0), it should be true that θi → _θ_0.
Asymptotic normality
[edit]
Assuming that consistency has been established and the derivatives of the sample Q n {\displaystyle Q_{n}} 
- ^ Newey & McFadden (1994), Theorem 2.1
- ^ Shi, Xiaoxia. "Lecture Notes: Asymptotic Normality of Extremum Estimators" (PDF).
- ^ Hayashi, Fumio (2000). Econometrics. Princeton: Princeton University Press. p. 448. ISBN 0-691-01018-8.
- ^ Hayashi, Fumio (2000). Econometrics. Princeton: Princeton University Press. p. 447. ISBN 0-691-01018-8.
- Amemiya, Takeshi (1985). "Asymptotic Properties of Extremum Estimators". Advanced Econometrics. Harvard University Press. pp. 105–158. ISBN 0-674-00560-0.
- Hayashi, Fumio (2000). "Extremum Estimators". Econometrics. Princeton: Princeton University Press. pp. 445–506. ISBN 0-691-01018-8.
- Newey, Whitney K.; McFadden, Daniel (1994). "Large sample estimation and hypothesis testing". Handbook of Econometrics. Vol. IV. Elsevier Science. pp. 2111–2245. doi:10.1016/S1573-4412(05)80005-4. ISBN 0-444-88766-0.