Gimbal lock (original) (raw)
From Wikipedia, the free encyclopedia
Loss of one degree of freedom in a three-dimensional, three-gimbal mechanism
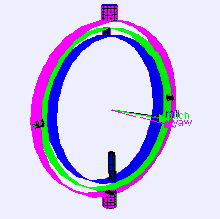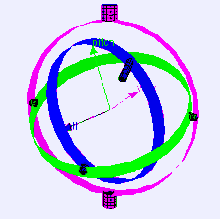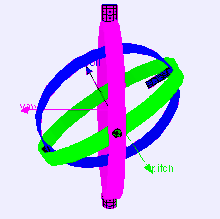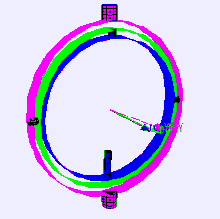
Gimbal locked airplane. When the pitch (green) and yaw (magenta) gimbals become aligned, changes to roll (blue) and yaw apply the same rotation to the airplane.
Adding a fourth rotational axis can solve the problem of gimbal lock, but it requires the outermost ring to be actively driven so that it stays 90 degrees out of alignment with the innermost axis (the flywheel shaft). Without active driving of the outermost ring, all four axes can become aligned in a plane as shown above, again leading to gimbal lock and inability to roll.
Gimbal lock is the loss of one degree of freedom in a multi-dimensional mechanism at certain alignments of the axes. In a three-dimensional three-gimbal mechanism, gimbal lock occurs when the axes of two of the gimbals are driven into a parallel configuration, "locking" the system into rotation in a degenerate two-dimensional space.
The term gimbal-lock can be misleading in the sense that none of the individual gimbals are actually restrained. All three gimbals can still rotate freely about their respective axes of suspension. Nevertheless, because of the parallel orientation of two of the gimbals' axes, there is no gimbal available to accommodate rotation about one axis, leaving the suspended object effectively locked (i.e. unable to rotate) around that axis.
The problem can be generalized to other contexts, where a coordinate system loses definition of one of its variables at certain values of the other variables.
A gimbal is a ring that is suspended so it can rotate about an axis. Gimbals are typically nested one within another to accommodate rotation about multiple axes.
They appear in gyroscopes and in inertial measurement units to allow the inner gimbal's orientation to remain fixed while the outer gimbal suspension assumes any orientation. In compasses and flywheel energy storage mechanisms they allow objects to remain upright. They are used to orient thrusters on rockets.[1]
Some coordinate systems in mathematics behave as if they were real gimbals used to measure the angles, notably Euler angles.
For cases of three or fewer nested gimbals, gimbal lock inevitably occurs at some point in the system due to properties of covering spaces.
While only two specific orientations produce exact gimbal lock, practical mechanical gimbals encounter difficulties near those orientations. When a set of gimbals is close to the locked configuration, small rotations of the gimbal platform require large motions of the surrounding gimbals. Although the ratio is infinite only at the point of gimbal lock, the practical speed and acceleration limits of the gimbals—due to inertia (resulting from the mass of each gimbal ring), bearing friction, the flow resistance of air or other fluid surrounding the gimbals (if they are not in a vacuum), and other physical and engineering factors—limit the motion of the platform close to that point.
Gimbal lock can occur in gimbal systems with two degrees of freedom such as a theodolite with rotations about an azimuth (horizontal angle) and elevation (vertical angle). These two-dimensional systems can gimbal lock at zenith and nadir, because at those points azimuth is not well-defined, and rotation in the azimuth direction does not change the direction the theodolite is pointing.
Consider tracking a helicopter flying towards the theodolite from the horizon. The theodolite is a telescope mounted on a tripod so that it can move in azimuth and elevation to track the helicopter. The helicopter flies towards the theodolite and is tracked by the telescope in elevation and azimuth. The helicopter flies immediately above the tripod (i.e. it is at zenith) when it changes direction and flies at 90 degrees to its previous course. The telescope cannot track this maneuver without a discontinuous jump in one or both of the gimbal orientations. There is no continuous motion that allows it to follow the target. It is in gimbal lock. So there is an infinity of directions around zenith for which the telescope cannot continuously track all movements of a target.[2] Note that even if the helicopter does not pass through zenith, but only near zenith, so that gimbal lock does not occur, the system must still move exceptionally rapidly to track it, as it rapidly passes from one bearing to the other. The closer to zenith the nearest point is, the faster this must be done, and if it actually goes through zenith, the limit of these "increasingly rapid" movements becomes infinitely fast, namely discontinuous.
To recover from gimbal lock the user has to go around the zenith – explicitly: reduce the elevation, change the azimuth to match the azimuth of the target, then change the elevation to match the target.
Mathematically, this corresponds to the fact that spherical coordinates do not define a coordinate chart on the sphere at zenith and nadir. Alternatively, the corresponding map _T_2→_S_2 from the torus _T_2 to the sphere _S_2 (given by the point with given azimuth and elevation) is not a covering map at these points.
In three dimensions
[edit]
Gimbal with 3 axes of rotation. A set of three gimbals mounted together to allow three degrees of freedom: roll, pitch and yaw. When two gimbals rotate around the same axis, the system loses one degree of freedom.
Normal situation: the three gimbals are independent
Gimbal lock: two out of the three gimbals are in the same plane, one degree of freedom is lost
Consider a case of a level-sensing platform on an aircraft flying due north with its three gimbal axes mutually perpendicular (i.e., roll, pitch and yaw angles each zero). If the aircraft pitches up 90 degrees, the aircraft and platform's yaw axis gimbal becomes parallel to the roll axis gimbal, and changes about yaw can no longer be compensated for.
This problem may be overcome by use of a fourth gimbal, actively driven by a motor so as to maintain a large angle between roll and yaw gimbal axes. Another solution is to rotate one or more of the gimbals to an arbitrary position when gimbal lock is detected and thus reset the device.
Modern practice is to avoid the use of gimbals entirely. In the context of inertial navigation systems, that can be done by mounting the inertial sensors directly to the body of the vehicle (this is called a strapdown system)[3] and integrating sensed rotation and acceleration digitally using quaternion methods to derive vehicle orientation and velocity. Another way to replace gimbals is to use fluid bearings or a flotation chamber.[4]
A well-known gimbal lock incident happened in the Apollo 11 Moon mission. On this spacecraft, a set of gimbals was used on an inertial measurement unit (IMU). The engineers were aware of the gimbal lock problem but had declined to use a fourth gimbal.[5] Some of the reasoning behind this decision is apparent from the following quote:
The advantages of the redundant gimbal seem to be outweighed by the equipment simplicity, size advantages, and corresponding implied reliability of the direct three degree of freedom unit.
— David Hoag, Apollo Lunar Surface Journal
They preferred an alternate solution using an indicator that would be triggered when near to 85 degrees pitch.
Near that point, in a closed stabilization loop, the torque motors could theoretically be commanded to flip the gimbal 180 degrees instantaneously. Instead, in the LM, the computer flashed a "gimbal lock" warning at 70 degrees and froze the IMU at 85 degrees
— Paul Fjeld, Apollo Lunar Surface Journal
Rather than try to drive the gimbals faster than they could go, the system simply gave up and froze the platform. From this point, the spacecraft would have to be manually moved away from the gimbal lock position, and the platform would have to be manually realigned using the stars as a reference.[6]
After the Lunar Module had landed, Mike Collins aboard the Command Module joked "How about sending me a fourth gimbal for Christmas?"
Industrial robot operating in a foundry.
In robotics, gimbal lock is commonly referred to as "wrist flip", due to the use of a "triple-roll wrist" in robotic arms, where three axes of the wrist, controlling yaw, pitch, and roll, all pass through a common point.
An example of a wrist flip, also called a wrist singularity, is when the path through which the robot is traveling causes the first and third axes of the robot's wrist to line up. The second wrist axis then attempts to spin 180° in zero time to maintain the orientation of the end effector. The result of a singularity can be quite dramatic and can have adverse effects on the robot arm, the end effector, and the process.
The importance of avoiding singularities in robotics has led the American National Standard for Industrial Robots and Robot Systems – Safety Requirements to define it as "a condition caused by the collinear alignment of two or more robot axes resulting in unpredictable robot motion and velocities".[7]
In applied mathematics
[edit]
The problem of gimbal lock appears when one uses Euler angles in applied mathematics; developers of 3D computer programs, such as 3D modeling, embedded navigation systems, and video games must take care to avoid it.
In formal language, gimbal lock occurs because the map from Euler angles to rotations (topologically, from the 3-torus T3 to the real projective space RP3, which is the same as the space of rotations for three-dimensional rigid bodies, formally named SO(3)) is not a local homeomorphism at every point, and thus at some points the rank (degrees of freedom) must drop below 3, at which point gimbal lock occurs. Euler angles provide a means for giving a numerical description of any rotation in three-dimensional space using three numbers, but not only is this description not unique, but there are some points where not every change in the target space (rotations) can be realized by a change in the source space (Euler angles). This is a topological constraint – there is no covering map from the 3-torus to the 3-dimensional real projective space; the only (non-trivial) covering map is from the 3-sphere, as in the use of quaternions.
To make a comparison, all the translations can be described using three numbers x {\displaystyle x} 








Loss of a degree of freedom with Euler angles
[edit]
A rotation in 3D space can be represented numerically with matrices in several ways. One of these representations is:
R = [ 1 0 0 0 cos α − sin α 0 sin α cos α ] [ cos β 0 sin β 0 1 0 − sin β 0 cos β ] [ cos γ − sin γ 0 sin γ cos γ 0 0 0 1 ] {\displaystyle {\begin{aligned}R&={\begin{bmatrix}1&0&0\\0&\cos \alpha &-\sin \alpha \\0&\sin \alpha &\cos \alpha \end{bmatrix}}{\begin{bmatrix}\cos \beta &0&\sin \beta \\0&1&0\\-\sin \beta &0&\cos \beta \end{bmatrix}}{\begin{bmatrix}\cos \gamma &-\sin \gamma &0\\\sin \gamma &\cos \gamma &0\\0&0&1\end{bmatrix}}\end{aligned}}}
An example worth examining happens when β = π 2 {\displaystyle \beta ={\tfrac {\pi }{2}}} 


R = [ 1 0 0 0 cos α − sin α 0 sin α cos α ] [ 0 0 1 0 1 0 − 1 0 0 ] [ cos γ − sin γ 0 sin γ cos γ 0 0 0 1 ] {\displaystyle {\begin{aligned}R&={\begin{bmatrix}1&0&0\\0&\cos \alpha &-\sin \alpha \\0&\sin \alpha &\cos \alpha \end{bmatrix}}{\begin{bmatrix}0&0&1\\0&1&0\\-1&0&0\end{bmatrix}}{\begin{bmatrix}\cos \gamma &-\sin \gamma &0\\\sin \gamma &\cos \gamma &0\\0&0&1\end{bmatrix}}\end{aligned}}}
Carrying out matrix multiplication:
R = [ 0 0 1 sin α cos α 0 − cos α sin α 0 ] [ cos γ − sin γ 0 sin γ cos γ 0 0 0 1 ] = [ 0 0 1 sin α cos γ + cos α sin γ − sin α sin γ + cos α cos γ 0 − cos α cos γ + sin α sin γ cos α sin γ + sin α cos γ 0 ] {\displaystyle {\begin{aligned}R&={\begin{bmatrix}0&0&1\\\sin \alpha &\cos \alpha &0\\-\cos \alpha &\sin \alpha &0\end{bmatrix}}{\begin{bmatrix}\cos \gamma &-\sin \gamma &0\\\sin \gamma &\cos \gamma &0\\0&0&1\end{bmatrix}}&={\begin{bmatrix}0&0&1\\\sin \alpha \cos \gamma +\cos \alpha \sin \gamma &-\sin \alpha \sin \gamma +\cos \alpha \cos \gamma &0\\-\cos \alpha \cos \gamma +\sin \alpha \sin \gamma &\cos \alpha \sin \gamma +\sin \alpha \cos \gamma &0\end{bmatrix}}\end{aligned}}}
And finally using the trigonometry formulas:
R = [ 0 0 1 sin ( α + γ ) cos ( α + γ ) 0 − cos ( α + γ ) sin ( α + γ ) 0 ] {\displaystyle {\begin{aligned}R&={\begin{bmatrix}0&0&1\\\sin(\alpha +\gamma )&\cos(\alpha +\gamma )&0\\-\cos(\alpha +\gamma )&\sin(\alpha +\gamma )&0\end{bmatrix}}\end{aligned}}}
Changing the values of α {\displaystyle \alpha } 






It is possible to imagine an airplane rotated by the above-mentioned Euler angles using the X-Y-Z convention. In this case, the first angle - α {\displaystyle \alpha } 


It is also possible to choose another convention for representing a rotation with a matrix using Euler angles than the X-Y-Z convention above, and also choose other variation intervals for the angles, but in the end there is always at least one value for which a degree of freedom is lost.
The gimbal lock problem does not make Euler angles "invalid" (they always serve as a well-defined coordinate system), but it makes them unsuited for some practical applications.
Alternate orientation representation
[edit]
The cause of gimbal lock is the representation of orientation in calculations as three axial rotations based on Euler angles. A potential solution therefore is to represent the orientation in some other way. This could be as a rotation matrix, a quaternion (see quaternions and spatial rotation), or a similar orientation representation that treats the orientation as a value rather than three separate and related values. Given such a representation, the user stores the orientation as a value. To quantify angular changes produced by a transformation, the orientation change is expressed as a delta angle/axis rotation. The resulting orientation must be re-normalized to prevent the accumulation of floating-point error in successive transformations. For matrices, re-normalizing the result requires converting the matrix into its nearest orthonormal representation. For quaternions, re-normalization requires performing quaternion normalization.
- Aircraft principal axes
- Charts on SO(3)
- Flight dynamics – Study of the performance, stability, and control of flying vehicles
- Grid north – Cartesian geographic coordinate systemPages displaying short descriptions of redirect targets (equivalent navigational problem on polar expeditions)
- Inertial navigation system – Continuously computed dead reckoning
- Motion planning – Computational problem
- Quaternions and spatial rotation – Correspondence between quaternions and 3D rotations
- Keyhole problem – Problems tracking near a gimbal axis under rate and acceleration limits
- ^ Jonathan Strickland (2008). "What is a gimbal -- and what does it have to do with NASA?".
- ^ Adrian Popa (June 4, 1998). "Re: What is meant by the term gimbal lock?".
- ^ Chris Verplaetse (1995). "Overview of Pen Design and Navigation Background". Archived from the original on 2009-02-14.
- ^ Chappell, Charles, D. (2006). "Articulated gas bearing support pads".
{{[cite web](/wiki/Template:Cite%5Fweb "Template:Cite web")}}: CS1 maint: multiple names: authors list (link) - ^ David Hoag (1963). "Apollo Guidance and Navigation - Considerations of Apollo IMU Gimbal Lock - MIT Instrumentation Laboratory Document E-1344". Archived from the original on 2021-08-27. Retrieved 2006-10-08.
- ^ Eric M. Jones; Paul Fjeld (2006). "Gimbal Angles, Gimbal Lock, and a Fourth Gimbal for Christmas". Archived from the original on 2009-05-29. Retrieved 2006-10-08.
- ^ ANSI/RIA R15.06-1999