Inscribed angle (original) (raw)
From Wikipedia, the free encyclopedia
Angle formed in the interior of a circle
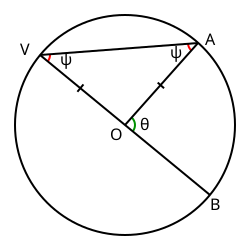
The inscribed angle θ circle.
In geometry, an inscribed angle is the angle formed in the interior of a circle when two chords intersect on the circle. It can also be defined as the angle subtended at a point on the circle by two given points on the circle.
Equivalently, an inscribed angle is defined by two chords of the circle sharing an endpoint.
The inscribed angle theorem relates the measure of an inscribed angle to that of the central angle intercepting the same arc.
The inscribed angle theorem appears as Proposition 20 in Book 3 of Euclid's Elements.
Note that this theorem is not to be confused with the Angle bisector theorem, which also involves angle bisection (but of an angle of a triangle not inscribed in a circle).
For fixed points A and B, the set of points M in the plane, for which the angle ∠AMB is equal to α, is an arc of a circle. The measure of ∠AOB, where O is the center of the circle, is 2_α_.
The inscribed angle theorem states that an angle θ inscribed in a circle is half of the central angle 2_θ_ that intercepts the same arc on the circle. Therefore, the angle does not change as its vertex is moved to different positions on the same arc of the circle.
Inscribed angles where one chord is a diameter
[edit]
Case: One chord is a diameter
Let O be the center of a circle, as in the diagram at right. Choose two points on the circle, and call them V and A. Designate point B to be diametrically opposite point V. Draw chord VB, a diameter containing point O. Draw chord VA. Angle ∠BVA is an inscribed angle that intercepts arc AB; denote it as ψ. Draw line OA. Angle ∠BOA is a central angle that also intercepts arc AB; denote it as θ.
Lines OV and OA are both radii of the circle, so they have equal lengths. Therefore, triangle △VOA is isosceles, so angle ∠BVA and angle ∠VAO are equal.
Angles ∠BOA and ∠AOV are supplementary, summing to a straight angle (180°), so angle ∠AOV measures 180° − θ.
The three angles of triangle △VOA must sum to 180°:
( 180 ∘ − θ ) + ψ + ψ = 180 ∘ . {\displaystyle (180^{\circ }-\theta )+\psi +\psi =180^{\circ }.} 
Adding θ − 180 ∘ {\displaystyle \theta -180^{\circ }} 
2 ψ = θ . {\displaystyle 2\psi =\theta .} 
Inscribed angles with the center of the circle in their interior
[edit]
Case: Center interior to angle
ψ_0 = ∠_DVC, θ_0 = ∠_DOC
ψ_1 = ∠_EVD, θ_1 = ∠_EOD
ψ_2 = ∠_EVC, θ_2 = ∠_EOC
Given a circle whose center is point O, choose three points V, C, D on the circle. Draw lines VC and VD: angle ∠DVC is an inscribed angle. Now draw line OV and extend it past point O so that it intersects the circle at point E. Angle ∠DVC intercepts arc DC on the circle.
Suppose this arc includes point E within it. Point E is diametrically opposite to point V. Angles ∠DVE, ∠EVC are also inscribed angles, but both of these angles have one side which passes through the center of the circle, therefore the theorem from the above Part 1 can be applied to them.
Therefore,
∠ D V C = ∠ D V E + ∠ E V C . {\displaystyle \angle DVC=\angle DVE+\angle EVC.} 
then let
ψ 0 = ∠ D V C , ψ 1 = ∠ D V E , ψ 2 = ∠ E V C , {\displaystyle {\begin{aligned}\psi _{0}&=\angle DVC,\\\psi _{1}&=\angle DVE,\\\psi _{2}&=\angle EVC,\end{aligned}}} 
so that
ψ 0 = ψ 1 + ψ 2 . ( 1 ) {\displaystyle \psi _{0}=\psi _{1}+\psi _{2}.\qquad \qquad (1)} 
Draw lines OC and OD. Angle ∠DOC is a central angle, but so are angles ∠DOE and ∠EOC, and ∠ D O C = ∠ D O E + ∠ E O C . {\displaystyle \angle DOC=\angle DOE+\angle EOC.} 
Let
θ 0 = ∠ D O C , θ 1 = ∠ D O E , θ 2 = ∠ E O C , {\displaystyle {\begin{aligned}\theta _{0}&=\angle DOC,\\\theta _{1}&=\angle DOE,\\\theta _{2}&=\angle EOC,\end{aligned}}} 
so that
θ 0 = θ 1 + θ 2 . ( 2 ) {\displaystyle \theta _{0}=\theta _{1}+\theta _{2}.\qquad \qquad (2)} 
From Part One we know that θ 1 = 2 ψ 1 {\displaystyle \theta _{1}=2\psi _{1}} 

θ 0 = 2 ψ 1 + 2 ψ 2 = 2 ( ψ 1 + ψ 2 ) {\displaystyle \theta _{0}=2\psi _{1}+2\psi _{2}=2(\psi _{1}+\psi _{2})} 
therefore, by equation (1),
θ 0 = 2 ψ 0 . {\displaystyle \theta _{0}=2\psi _{0}.} 
Inscribed angles with the center of the circle in their exterior
[edit]
Case: Center exterior to angle
ψ_0 = ∠_DVC, θ_0 = ∠_DOC
ψ_1 = ∠_EVD, θ_1 = ∠_EOD
ψ_2 = ∠_EVC, θ_2 = ∠_EOC
The previous case can be extended to cover the case where the measure of the inscribed angle is the difference between two inscribed angles as discussed in the first part of this proof.
Given a circle whose center is point O, choose three points V, C, D on the circle. Draw lines VC and VD: angle ∠DVC is an inscribed angle. Now draw line OV and extend it past point O so that it intersects the circle at point E. Angle ∠DVC intercepts arc DC on the circle.
Suppose this arc does not include point E within it. Point E is diametrically opposite to point V. Angles ∠EVD, ∠EVC are also inscribed angles, but both of these angles have one side which passes through the center of the circle, therefore the theorem from the above Part 1 can be applied to them.
Therefore,
∠ D V C = ∠ E V C − ∠ E V D . {\displaystyle \angle DVC=\angle EVC-\angle EVD.} 
then let
ψ 0 = ∠ D V C , ψ 1 = ∠ E V D , ψ 2 = ∠ E V C , {\displaystyle {\begin{aligned}\psi _{0}&=\angle DVC,\\\psi _{1}&=\angle EVD,\\\psi _{2}&=\angle EVC,\end{aligned}}} 
so that
ψ 0 = ψ 2 − ψ 1 . ( 3 ) {\displaystyle \psi _{0}=\psi _{2}-\psi _{1}.\qquad \qquad (3)} 
Draw lines OC and OD. Angle ∠DOC is a central angle, but so are angles ∠EOD and ∠EOC, and
∠ D O C = ∠ E O C − ∠ E O D . {\displaystyle \angle DOC=\angle EOC-\angle EOD.} 
Let
θ 0 = ∠ D O C , θ 1 = ∠ E O D , θ 2 = ∠ E O C , {\displaystyle {\begin{aligned}\theta _{0}&=\angle DOC,\\\theta _{1}&=\angle EOD,\\\theta _{2}&=\angle EOC,\end{aligned}}} 
so that
θ 0 = θ 2 − θ 1 . ( 4 ) {\displaystyle \theta _{0}=\theta _{2}-\theta _{1}.\qquad \qquad (4)} 
From Part One we know that θ 1 = 2 ψ 1 {\displaystyle \theta _{1}=2\psi _{1}} 



Animated gif of proof of the inscribed angle theorem. The large triangle that is inscribed in the circle gets subdivided into three smaller triangles, all of which are isosceles because their upper two sides are radii of the circle. Inside each isosceles triangle the pair of base angles are equal to each other, and are half of 180° minus the apex angle at the circle's center. Adding up these isosceles base angles yields the theorem, namely that the inscribed angle, ψ, is half the central angle, θ.
The angle θ between a chord and a tangent is half the arc belonging to the chord.
By a similar argument, the angle between a chord and the tangent line at one of its intersection points equals half of the central angle subtended by the chord. See also Tangent lines to circles.
Proof without words using the inscribed angle theorem that opposite angles of a cyclic quadrilateral are supplementary:
2𝜃 + 2𝜙 = 360° ∴ 𝜃 + 𝜙 = 180°
The inscribed angle theorem is used in many proofs of elementary Euclidean geometry of the plane. A special case of the theorem is Thales's theorem, which states that the angle subtended by a diameter is always 90°, i.e., a right angle. As a consequence of the theorem, opposite angles of cyclic quadrilaterals sum to 180°; conversely, any quadrilateral for which this is true can be inscribed in a circle. As another example, the inscribed angle theorem is the basis for several theorems related to the power of a point with respect to a circle. Further, it allows one to prove that when two chords intersect in a circle, the products of the lengths of their pieces are equal.
Inscribed angle theorems for ellipses, hyperbolas and parabolas
[edit]
Inscribed angle theorems exist for ellipses, hyperbolas and parabolas too. The essential differences are the measurements of an angle. (An angle is considered a pair of intersecting lines.)
- Ellipse
- Hyperbola
- Parabola
- Ogilvy, C. S. (1990). Excursions in Geometry. Dover. pp. 17–23. ISBN 0-486-26530-7.
- Gellert W, Küstner H, Hellwich M, Kästner H (1977). The VNR Concise Encyclopedia of Mathematics. New York: Van Nostrand Reinhold. p. 172. ISBN 0-442-22646-2.
- Moise, Edwin E. (1974). Elementary Geometry from an Advanced Standpoint (2nd ed.). Reading: Addison-Wesley. pp. 192–197. ISBN 0-201-04793-4.
- Weisstein, Eric W. "Inscribed Angle". MathWorld.
- Relationship Between Central Angle and Inscribed Angle
- Munching on Inscribed Angles at cut-the-knot
- Arc Central Angle With interactive animation
- Arc Peripheral (inscribed) Angle With interactive animation
- Arc Central Angle Theorem With interactive animation
- At bookofproofs.github.io