Thermal ionization (original) (raw)
From Wikipedia, the free encyclopedia
Process in which atoms are released from a hot surface, and are ionized
Thermal ionization, also known as surface ionization or contact ionization, is a physical process whereby the atoms are desorbed from a hot surface, and in the process are ionized.
Thermal ionization is used to make simple ion sources, for mass spectrometry and for generating ion beams.[1] Thermal ionization has seen extensive use in determining atomic weights, in addition to being used in many geological/nuclear applications.[2]
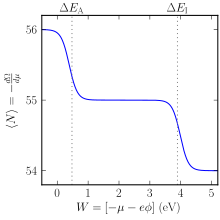
Surface ionization effect in a vaporized cesium atom at 1500 K, calculated using a grand canonical ensemble. Y-axis: average number of electrons on the atom; the atom is neutral when it has 55 electrons. X-axis: energy variable (equal to the surface work function) dependent on electron chemical potential μ and electrostatic potential ϕ.
The likelihood of ionization is a function of the filament temperature, the work function of the filament substrate and the ionization energy of the element.
This is summarised in the Saha–Langmuir equation:[3]
n + n 0 = g + g 0 exp ( W − Δ E I k T ) {\displaystyle {\frac {n_{+}}{n_{0}}}={\frac {g_{+}}{g_{0}}}\exp {\Bigg (}{\frac {W-\Delta E_{\text{I}}}{kT}}{\Bigg )}}
where
n + n 0 {\displaystyle {\frac {n_{+}}{n_{0}}}} 
g + g 0 {\displaystyle {\frac {g_{+}}{g_{0}}}} 
W {\displaystyle W} 
Δ E I {\displaystyle \Delta E_{\text{I}}} 
k {\displaystyle k} 
T {\displaystyle T} 
Negative ionization can also occur for elements with a large electron affinity Δ E A {\displaystyle \Delta E_{\text{A}}} 
Thermal ionization mass spectrometry
[edit]
One application of thermal ionization is thermal ionization mass spectrometry (TIMS). In thermal ionization mass spectrometry, a chemically purified material is placed onto a filament which is then heated to high temperatures to cause some of the material to be ionized as it is thermally desorbed (boiled off) the hot filament. Filaments are generally flat pieces of metal around 1–2 mm (0.039–0.079 in) wide, 0.1 mm (0.0039 in) thick, bent into an upside-down U shape and attached to two contacts that supply a current.
This method is widely used in radiometric dating, where the sample is ionized under vacuum. The ions being produced at the filament are focused into an ion beam and then passed through a magnetic field to separate them by mass. The relative abundances of different isotopes can then be measured, yielding isotope ratios.
When these isotope ratios are measured by TIMS, mass-dependent fractionation occurs as species are emitted by the hot filament. Fractionation occurs due to the excitation of the sample and therefore must be corrected for accurate measurement of the isotope ratio.[4]
There are several advantages of the TIMS method. It has a simple design, is less expensive than other mass spectrometers, and produces stable ion emissions. It requires a stable power supply, and is suitable for species with a low ionization energy, such as strontium and lead.
The disadvantages of this method stem from the maximum temperature achieved in thermal ionization. The hot filament reaches a temperature of less than 2,500 °C (2,770 K; 4,530 °F), leading to the inability to create atomic ions of species with a high ionization energy, such as osmium and tungsten. Although the TIMS method can create molecular ions instead in this case, species with high ionization energy can be analyzed more effectively with MC-ICP-MS.[_citation needed_]
- ^ Alton, G. D. (1988). "Characterization of a cesium surface ionization source with a porous tungsten ionizer. I" (PDF). Review of Scientific Instruments. 59 (7): 1039–1044. Bibcode:1988RScI...59.1039A. doi:10.1063/1.1139776. ISSN 0034-6748.
- ^ Barshick, C; Duckworth, D; Smith, D (2000). Inorganic mass spectrometry : fundamentals and applications. New York, NY [u.a.]: Dekker. p. 1. ISBN 9780824702434.
- ^ Dresser, M. J. (January 1968). "The Saha-Langmuir Equation and its Application" (PDF). Journal of Applied Physics. 39 (1): 338–339. Bibcode:1968JAP....39..338D. doi:10.1063/1.1655755. Retrieved 2007-10-11.
- ^ Dickin, A.P., 2005. Radiogenic Isotope Geology 2nd ed. Cambridge: Cambridge University Press. pp. 21–22