Libellus de quinque corporibus regularibus (original) (raw)
| Libellus de quinque corporibus regularibus | |
|---|---|
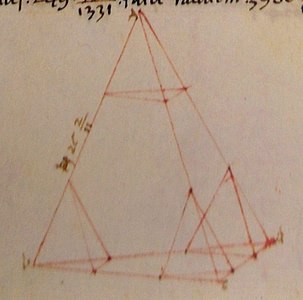
 Première page du codex Première page du codex |
|
| Auteur | Piero della Francesca |
| Pays |  Italie Italie |
| Genre | codex |
| Version originale | |
| Langue | Toscan et latin |
| Titre | Libellus de quinque corporibus regularibus |
| Date de parution | circa 1480 |
modifier  |
Libellus de quinque corporibus regularibus (Les cinq polyèdres réguliers) est un traité de mathématiques écrit par Piero della Francesca. La datation en est incertaine, mais se situe entre les années 1480 et 1492. Le traité est une réécriture et augmentation de la partie géométrique de son Trattato d'abaco. Plus de la moitié des problèmes sont nouveaux et surtout il y a des découvertes mathématiques importantes.
- Il existe un seul codex du Libellus de quinque corporibus regularibus, qui se trouve à la Biblioteca Apostolica Vaticana, MS. Urb.lat.632[1]. Une édition critique et reproduction en facsimilé a été publiée en 1995[2].
- Une copie de chaque page du codex est visible sur Commons : Libellus De Quinque Corporibus Regularibus
Peu de temps après la mort de Piero en 1492, le Libellus et le Trattato d'abaco étaient plagiés par Luca Pacioli et publiés dans ses livres De divina proportione[3] (1509) et Summa de arithmetica, geometria, de proportioni et de proportionalita (Venise, 1494), sans citer Piero (voire Plagiat par Luca Pacioli pour plus de détails). C'est ainsi que ses œuvres mathématiques se sont pas passées à la postérité et Piero lui-même est tombé dans un oubli quasi-total pendant 450 ans.
Au milieu du XIXe siècle, avec l’engouement européen pour le début de la Renaissance, les tableaux de Piero della Francesca ont été réévalués. L'aspect mathématique de son œuvre était souvent relégué à référence à Luca Pacioli, l'élève qui a surpassé le maître[4].
- En 1915 G. Mancini a formellement identifié[5] un codex qui se trouvait dans la bibliothèque du Vatican, et signalé par G. Pitarelli en 1903, comme étant le Libellus de Piero. Les annotations dans les marges et sur certains dessins étaient de la main même de Piero.
Cependant le Libellus avait été retrouvé à au moins deux reprises avant 1903 :
- En 1880, l'historien Max Jordan retrouvait le Libellus parmi les manuscrits de la collection d'Urbino dans la bibliothèque du Vatican. Une comparaison avec le Divina Proportione, de Pacioli, publié en 1509, révélait que le Libellus de Pacioli était simplement la traduction en italien du Libellus de Piero[6].
- James Dennistoun, dans son ouvrage Memoirs of the Dukes of Urbino, publié en 1851, a identifié[4] le manuscrit : Vat. Urb.632[7] comme étant le Libellus de Piero. (Dennistoun affirme également que le codex Vat Urb.1374[8] soit aussi l’œuvre de Piero, mais ne donne pas de détails. Il semble que cette affirmation soit erronée et ce codex une copie (circa 1460) de Perspectiva communis de John Peckham).
Le traité est dédié au jeune duc Guidobaldo Ier de Montefeltro, qui, à l'âge de 10 ans, succède à son père Frédéric III de Montefeltro en 1482, dont le cour est décrit par Baldassare Castiglione dans Le Livre du courtisan.
Dans le langage fleuri de la dédicace on peut apprécier l'importance que Piero accordait au traité et ses motivations pour l'écrire.
La première page de la dédicace est consacrée principalement à l’éloge des ducs d'Urrbino et en particulier du père de Guidobaldo. C'est sur la deuxième page que Piero devint un peu plus personnel et laisse entrevoir l'importance qu'il donne à son Libellus.
Piero écrit qu'il souhaite que le texte soit conservé à côté d'un précédent texte de lui qu'il avait dédié au père de Guidobaldo et qui s'appelle De Prospectiva[Note 1] :
« Et libellum ipsum inter innumera amplissimae tuae, paternaeq(ue) bibliothecae volumina penes aliud nostrum de Prospectiva opusculum, quod superioribus annis edidimus, pro pedissequo et aliorum servulo uel in angulo collocare »
« Et ranger ce livre, parmi les innombrables volumes de ta très ample bibliothèque paternelle, dans un coin près de notre autre ouvrage De Prospectiva, que nous avons écrit il y a plusieurs années, comme petit serviteur des autres »
En même temps Piero minimise la portée de ses travaux dans des termes très obséquieux :
« Non enim solent non admitti quandoque in opulentissima et lautissima mensa, agrestia et a rudi et inepto colono poma suscepta »
« Car on n'a pas coutume de refuser, même à une opulente table, les fruits rustiques qu'un paysan inculte et inepte apporte »
Il est évident qu'il pense le contraire et ajoute :
« Poterit namque saltem sui novitate non displicere »
« Évidemment, par rapport à son innovation, il ne peut pas déplaire »
Celle-ci est la seule phrase que Piero utilise pour dire qu'il a fait quelque chose de nouveau en géométrie depuis Euclide.
L'objet du traité est dit implicitement par Piero :
« Et enim licet res apud Euclidem, et alios geometras nota sit, per ipsum tamen nuper ad arithmetricos translata est »
« Et il est en fait possible que la chose ait été connue d'Euclide, et par d'autres géomètres, mais c'est par lui (Ce traité) qu'elle a cependant été transmise aux mathématiciens »
Dans son Liber abaci, Leonardo Fibonacci avait commencé l'arithmétisation de la géométrie d'Euclide, première étape vers la géométrie analytique. Fibonacci s'est limité à la géométrie plane, laissant les livres XIII à XV d'Euclide qui traitent la géométrie des solides réguliers. C'est cette lacune que Piero comble dans la deuxième partie du Libellus.
À la fin de sa dédicace Piero affirme qu'il considère le Libellus comme le monument de sa vie :
« Eritque pignus et monumentum mei, in te inclitamq(ue) prosapiem tuam antiqui amoris et perpetuae servitutis. »
« Et ce sera un gage, et mon accomplissement, pour toi et ton illustre lignée, de mon ancienne amitié et de ma perpétuelle soumission »
Le traité ne fait pas partie d'un genre existant, tel que le Trattato d'abaco. Comme pour De prospectica pingendi il est de conception originale et surtout de contenu original. Son projet, dit implicitement dans sa dédicace, est très ambitieux, c'est de compléter l’arithmétisation de la géométrie, commencée par Fibonacci dans son Liber abaci. Le travail de Piero est un précurseur de la géométrie analytique de Descartes.
Le Libellus est divisé en quatre livres :
I : Figures géométriques planes, qui reprend les démonstrations de Fibonacci.
II : Polyèdres inscrits dans une sphère, qui est l'application à trois dimensions du programme de Fibonacci.
III : Polyèdres inscrits dans d'autres polyèdres ; Piero propose de nouvelles relations entre certains polyèdres qui ne sont pas dans Euclide.
IV : Polyèdres « semi-réguliers », Piero fait une découverte indépendante des polyèdres d'Archimède
L'inspiration du traité de Piero se trouve dans les livres XIII, XIV et XV des Éléments d'Euclide qui culminent dans la description, la construction et l'analyse des relations qui existent entre les cinq polyèdres de Platon. Piero avait déjà commence ce projet dans la section sur la géométrie du Trattato d'abaco. En effet un peu plus que la moitié des problèmes des livres I - III se trouvait dans le Trattao d'abaco, mais Piero les reformule pour être plus clair et plus concis. Le livre IV est complètement nouveau.
Les 44 pages de la première partie du Libellus (f1.r - f23v) sont consacrées à 57 exercices de géométrie plane (polygones, cercles, etc.) et le calcul de divers éléments en fonction de dimensions données. Fibonacci avait déjà fait ce travail et cette première partie du Libellus est un rappel et mise en bouche par Piero pour la suite, qui est le traitement de la géométrie en trois dimensions, un travail originel de Piero.
Piero passe en revue les méthodes utilisées par Fibonacci dans son Liber abaci pour l’arithmétisation de la géométrie plane, c'est-à-dire dans un langage moderne : calculer les coordonnées de chaque point ; calculer des aires, etc. numériquement. De ce point de vue on peut transformer les constructions euclidiennes en problèmes d'arithmétique, allant de la construction d'un pentagone avec règle et compas à une formule pour son aire en fonction de la longueur d'un côté.
Fibonacci et Piero sont très handicapés dans leurs démonstrations par un problème de notation. L'idée que l'on peut représenter un chiffre quelconque par un symbole x , a , Z {\displaystyle x,a,Z} 
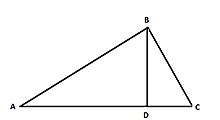
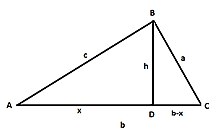
L'opération de base de Piero, et traitée dans le problème N°1, est la projection orthogonale d'un segment de ligne droite sur une autre ligne droite et est illustrée dans le cas d'un triangle A B C {\displaystyle ABC} 




Tous les algorithmes de Piero sont basés sur l'utilisation très habile du théorème de Pythagore et la projection orthogonale. Pour le lecteur qui désire suivre le raisonnement de Piero, les détails sont exposés dans les boîtes déroulantes ci-dessous (avec une notation symbolique, pour faciliter l'exposé.
Projection orthogonale, altitude et aire d'un triangle - la formule de Héron
D'abord un rappel du théorème de Pythagore : pour un triangle rectangle, de côtés de longueurs a , b , c , {\displaystyle a,b,c,} 

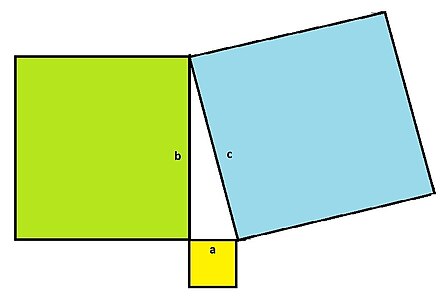
Démonstration visuelle du théorème de Pythagore
Le théorème de Pythagore affirme que dans un triangle rectangle, l'aire du carré construit sur l’hypoténuse est égale à la somme des aires des carrés construits sur les deux autres côtés (en symboles c 2 = a 2 + b 2 {\displaystyle c^{2}=a^{2}+b^{2}} 
Il n'est pas de tout évident que c'est vrai !
Démonstration :
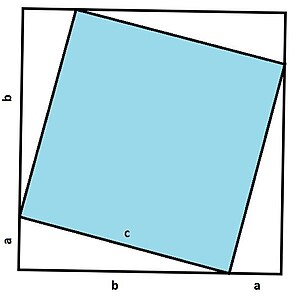
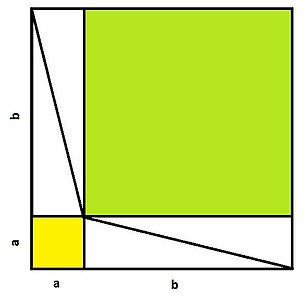
Si on place quatre copies du triangle dans un cadre de côté ( a + b ) {\displaystyle (a+b)} 
Considérons les deux façons de placer les quatre copies des triangles :
Donc, l'aire du carré sur l'hypoténuse (partie bleue du cadre non couvert dans la première configuration) est égale à la somme des aires des carrés sur les deux autres côtés (les aires jaune et verte, la partie du cadre non couvert dans la deuxième configuration) : le théorème de Pythagore.
Étant donnés les côtés a , b , c {\displaystyle a,b,c} 

La démonstration, suivant les règles de Piero, mais en utilisant des symboles est une double application du théorème de Pythagore :
Applique Pythagore au triangle rectangle A B D {\displaystyle ABD} 
Applique Pythagore au triangle rectangle C D B {\displaystyle CDB} 
Par substitution de h 2 {\displaystyle h^{2}} 
Donc, 2 b x = c 2 + b 2 − a 2 {\displaystyle 2bx=c^{2}+b^{2}-a^{2}} 

La hauteur h {\displaystyle h} 


Si on pousse la représentation symbolique des règles de Piero un peu plus loin on obtient la célèbre formule de Héron qui donne l'aire d'un triangle en fonction des longueurs des côtés :
La formule de Héron
Calculer h {\displaystyle h} 
h 2 = a 2 − ( b − c 2 + b 2 − a 2 2 b ) 2 = a 2 − ( 2 b 2 − c 2 − b 2 + a 2 2 b ) 2 = a 2 − ( a 2 + b 2 − c 2 2 b ) 2 {\displaystyle h^{2}=a^{2}-\left(b-{\frac {c^{2}+b^{2}-a^{2}}{2b}}\right)^{2}=a^{2}-\left({\frac {2b^{2}-c^{2}-b^{2}+a^{2}}{2b}}\right)^{2}=a^{2}-\left({\frac {a^{2}+b^{2}-c^{2}}{2b}}\right)^{2}}
Pour simplifier l'expression algébrique, on applique l'identité remarquable : X 2 − Y 2 = ( X − Y ) ( X + Y ) {\displaystyle X^{2}-Y^{2}=(X-Y)(X+Y)} 
h 2 = ( a − a 2 + b 2 − c 2 2 b ) ( a + a 2 + b 2 − c 2 2 b ) = ( 2 a b − a 2 − b 2 + c 2 2 b ) ( 2 a b + a 2 + b 2 − c 2 2 b ) = ( c 2 − ( a − b ) 2 2 b ) ( ( a + b ) 2 − c 2 2 b ) {\displaystyle h^{2}=\left(a-{\frac {a^{2}+b^{2}-c^{2}}{2b}}\right)\left(a+{\frac {a^{2}+b^{2}-c^{2}}{2b}}\right)=\left({\frac {2ab-a^{2}-b^{2}+c^{2}}{2b}}\right)\left({\frac {2ab+a^{2}+b^{2}-c^{2}}{2b}}\right)=\left({\frac {c^{2}-(a-b)^{2}}{2b}}\right)\left({\frac {(a+b)^{2}-c^{2}}{2b}}\right)}
Appliquons l'identité remarquable encore deux fois :
h 2 = ( c − a + b ) ( c + a − b ) ( a + b − c ) ( a + b + c ) 4 b 2 {\displaystyle h^{2}={\frac {(c-a+b)(c+a-b)(a+b-c)(a+b+c)}{4b^{2}}}}
Il est de coutume de noter s = 1 2 ( a + b + c ) {\displaystyle s={\frac {1}{2}}(a+b+c)} 
h 2 = ( 2 s − 2 a ) ( 2 s − 2 b ) ( 2 s − 2 c ) 2 S 4 b 2 = 4 s ( s − a ) ( s − b ) ( s − c ) b 2 {\displaystyle h^{2}={\frac {(2s-2a)(2s-2b)(2s-2c)2S}{4b^{2}}}={\frac {4s(s-a)(s-b)(s-c)}{b^{2}}}}
L'aire, A {\displaystyle A} 
A = 1 2 h b {\displaystyle A={\frac {1}{2}}hb} 

Il existe cinq, et seulement cinq, polyèdres convexes avec chaque face la même polygone régulier et à chaque vertex le même nombre d'arêtes : les polyèdres de Platon, les quinque corporibus regularibus du titre de l’œuvre. Les sommets de chaque polyèdre de Platon se situent sur la surface d'une sphère.
Ce livre (codex f24r - 37v) contient 37 problèmes. Piero calcule aires et volumes à partir des longueurs des arêtes des polyèdres, rayons des sphères qui les circonscrivent, etc. Le problème 37 est un problème « inverse » : le volume est connu, il faut calculer la longueur d'un arête :
Problème 37 (f.37.r) : Étant donné un icosaèdre de volume 400 brachia (sic), quelle est la longueur d'une arête ?
Le résultat donné par Piero après une page de calcul, aidé par un dessin de l'icosaèdre, est ( 8064000 − 59719680000 ) 1 6 {\displaystyle (8064000-{\sqrt {59719680000}})^{\frac {1}{6}}} 
Il est évident qu'un tel calcul n'est utile ni à un marchand, ni à un artiste. Si Piero le fait c'est pour d'autres raisons. La solution demande la résolution d'une équation cubique et Piero avait consacré une partie du Trattato d'abaco à ses tentatives de trouver des racines d'équations des troisième, quatrième et cinquième degrés. Piero n'avait pas réussi en général, mais dans ce cas particulier ses méthodes mènent à la solution (le problème de trouver les racines d'une équation cubique ou d'une équation quartique était résolu par Tartaglia et Ferrari au XVIe siècle et pour les équations de degré cinq par Niels Abel et Évariste Galois au XIXe siècle).
Logiquement le problème suivant n'a pas sa place dans ce livre, car il traite d'un tétraèdre général, pas le tétraèdre régulier. Mais, Piero était probablement très fier de son résultat, car c'est, au fond, le généralisation en trois dimensions de la formule de Héron d'Alexandrie qui donne l'aire d'un triangle en fonction des longueurs des côtés. Piero avait déjà publié le problème dans le Trattato d'abaco, mais sans la démonstration.
Problème 11 : Trouver la hauteur d'un tétraèdre général étant données les longueurs des côtés.
Le résultat est nouveau et combiné avec le fait, connu depuis Archimède, que le volume d'un tétraèdre général est égal au produit de la hauteur et l'aire de sa base divisé par trois, donne une formule pour le volume d'un tétraèdre en fonction des côtés.
L'idée de base de Piero est la suivante : à partir d'un tétraèdre général on peut construire un triangle qui a la même hauteur que le tétraèdre et dont on connait les longueurs des trois côtés et donc on peut calculer la hauteur.
Comment construire ce triangle ? La solution de Piero est ingénieuse et le lecteur est invité à la retrouver lui-même avant d'apprécier la construction de Piero, qui utilise uniquement le théorème de Pythagore et la projection orthogonale.
Méthode de Piero pour trouver la hauteur d'un tétraèdre
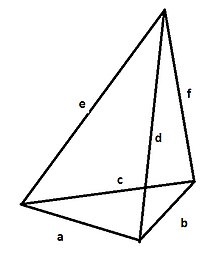
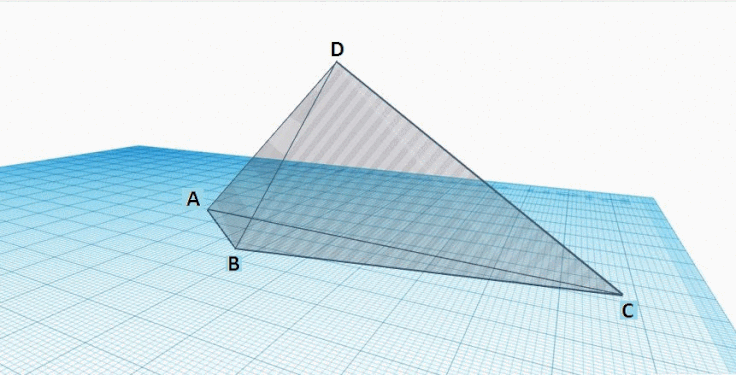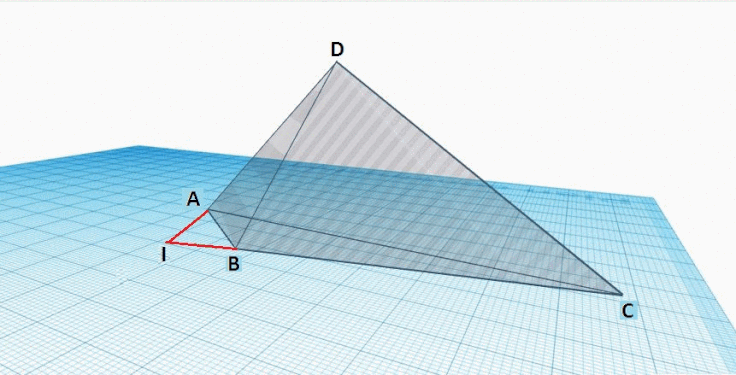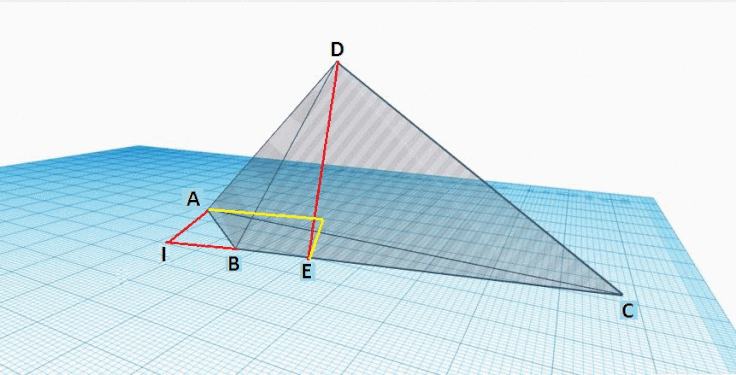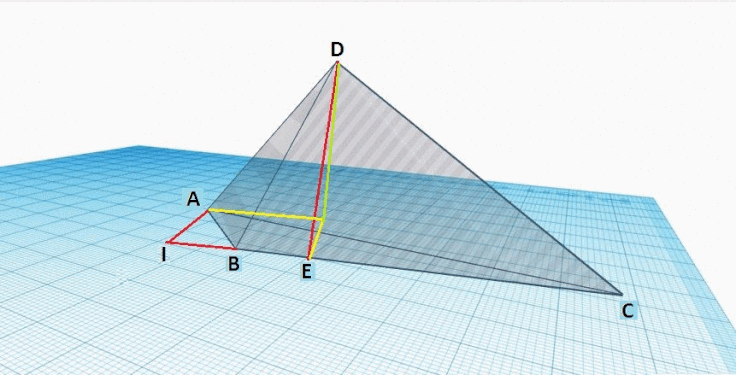
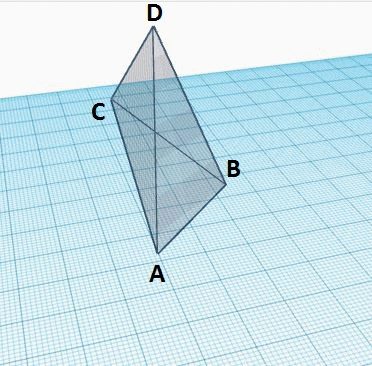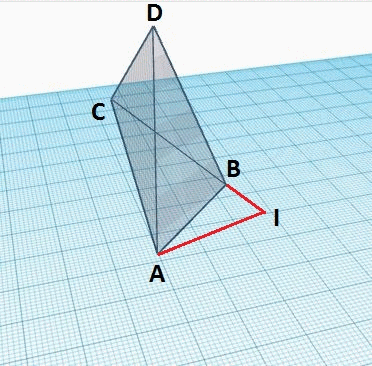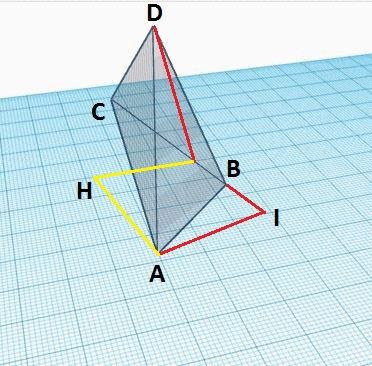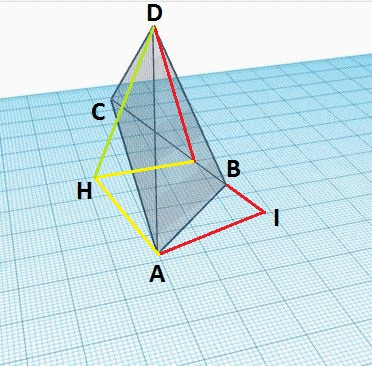
Les figures ci-dessous représentent le tétraèdre général A B C D {\displaystyle ABCD} 

La construction du triangle clef se fait en plusieurs étapes et à chaque étape on peut calculer les nouvelles longueurs qui sont introduites à partir des longueurs qui sont déjà connues.
Les longueurs : A B , B C , A C , A D , B D , C D {\displaystyle AB,BC,AC,AD,BD,CD} 
Étape 1 : Sur la face triangulaire D B C {\displaystyle DBC} 




Étape 2 : Sur la face triangulaire A B C {\displaystyle ABC} 




Étape 3 : Trace (jaune) la ligne E H {\displaystyle EH} 




Étape 4 : Tracer (vert) la ligne D H {\displaystyle DH} 





Finalement, regarder le triangle H D E {\displaystyle HDE} 


La transcription de l’algorithme de Piero en notation symbolique ne pose aucun problème. Les formules symboliques peut être consultées dans l'article Tétrahedron (en).
Ce résultat originel de Piero fut publié dans le plagiat du Trattato d'abaco par Luca Pacioli dans son _Summa Arithetica_en 1494 (mais sans la démonstration) puis dans son plagiat du Libellus dans son Divina Proportione en 1509, avec la démonstration de Piero. Cependant, la formule correspondante n'a jamais été très bien connue, car au XIXe siècle J.J. Sylvester en 1852, dans un article[9] où il étudiait des problèmes semblables il posait la question dans une 'Note' en bas de page : Quaere : Is not this expression for the volume of a pyramid in terms of its sides to be found in some previous writer? It can hardly have escaped inquiry.
Le but de cette partie du Libellus (codex f38.r - f49.r, qui comporte 29 problèmes) est l'arithmétisation d'Euclide, XV, qui trait les rapports des polyèdres de Platon entre eux. Piero traite les propositions d'Euclide et ajoute quelques découvertes qu'il a faites lui-même.
Piero commence ce livre en reprenant des propositions d'Euclide, XV.
Le premier problème est apparemment banal.
Problème 1 : Trouver le côté de l’octaèdre inscrit dans le tétraèdre de côté 12. (Les six sommets de l'octaèdre sont placés au milieu des six arêtes du tétraèdre). Le résultat est 6 et simple à trouver.
La solution de Piero est très longue et complexe, il utilise toutes les techniques à sa disposition; il fait des projections orthogonales peu évidentes, cherche des triangles similaires bien cachés, doit reconnaître que 108 − 12 = 48 {\displaystyle {\sqrt {108}}-{\sqrt {12}}={\sqrt {48}}} 

On peut se demander pourquoi Piero a choisi de donner une solution si complexe à son premier problème quand il savait qu'il existait des méthodes de solution très simples ? Il ne le fait plus jamais par la suite.
Il est possible que Piero était troublé par une question de philosophie mathématique : à savoir si l'arithmétique était assez complète et puissante pour décrire toutes les constructions géométriques d'Euclide et qui ne donnait pas des réponses contradictoires. Piero semble vouloir tester l'arithmétique en choisissant des chemins vers la solution qui sont longs et tortueux pour voir s'il obtient toujours la même solution numérique. Ce problème philosophique fut clarifié seulement au XXe siècle avec les travaux de David Hilbert, Kurt Gödel et Alan Turing.
Problème 2 : Un tétraèdre inscrit dans un cube : on place les six sommets du tétraèdre au milieu des six arêtes du cube (Euclide XV, 1).
Problème 3 : Si un octaèdre est inscrit dans un cube de côté 12, quelle est la longueur d'un arête de l'octaèdre ?
Cependant, Piero va plus loin qu'Euclide et découvre des nouvelles relations entre les solides de Platon.
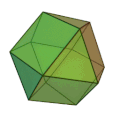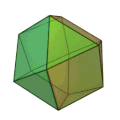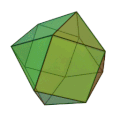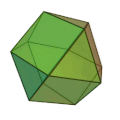
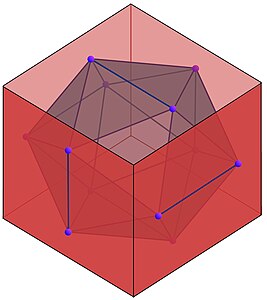
Problème 4 : Inscription d'un icosaèdre dans un cube. On peut orienter un icosaèdre tel que chaque face du cube contient deux sommets de l'icosaèdre. Cette relation entre un cube et un icosaèdre n'est pas décrite par Euclide, elle était une découverte nouvelle de Piero et a marqué le début de la fascination de la Renaissance pour la géométrie des polyèdres.
Icosaèdre inscrit dans un cube
  |
|---|
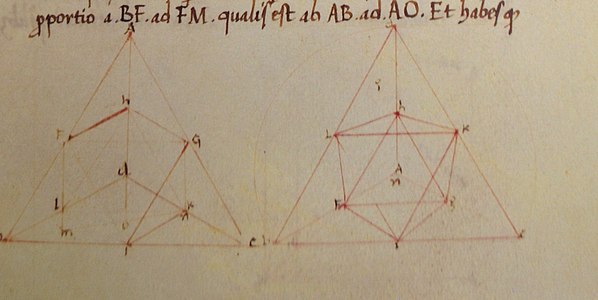
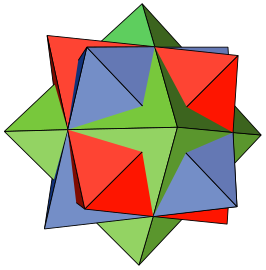
Problème 5 : Inscription d'un cube dans un octaèdre. Une inscription évidente est que les huit sommets du cube sont les centres des huit faces de l'octaèdre. Piero propose une autre façon, nettement moins évidente : les huit sommets du cube sont les milieux de huit des douze arêtes de l'octaèdre. Malheureusement, le dessin de Piero (ci-dessous), est un peu effacé. Avec ce mode d'inscription on peut inscrire deux autres cubes dans l'octaèdre. Si on le fait, puis on efface l'octaèdre on obtient le Composé de trois cubes (en). Au lieu de voir un cube inscrit dans un octaèdre, on peut voir un octaèdre circonscrit autour d'un cube et, comme précédemment, on peut circonscrire deux autres octaèdres autour du cube. Puis, si on efface le cube on obtient le Composé de trois octaèdres (en). Piero ne dessine pas les polyèdres composés dans le Libellus.
Les polyèdres composés sont redécouverts au début du XXe siècle et utilisés par l'artiste M.C. Escher dans plusieurs gravures.
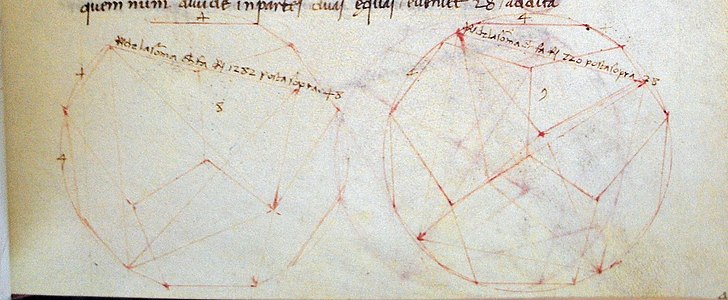
Problème 9 : Piero étudie un octaèdre inscrit dans un dodécaèdre (Euclide XV, 9) et fait ses calculs habituels. Mais il va plus loin qu'Euclide et découvre un théorème géométrique qu'Euclide aurait pu démontrer, mais il n'a pas fait.
Le diamètre de la sphère qui circonscrit l'octaèdre est égal à la longueur d'un arête + la longueur d'une corde d'une face pentagonale.
Octaèdre inscrit dans un dodécaèdre
  |
|---|
Piero donne une démonstration par computation.
Le but principal de cette partie du Libellus (codex f49v - f68.r, qui comporte 17 problèmes) est l'étude des solides « semi-réguliers » (c'est-à-dire des polyèdres dont chaque face est un polygone régulier, mais pas forcément le même) que l'on peut construire à partir des solides de Platon. Piero les obtient par troncation de chacun des 5 solides. Il décrit 6 solides, car il trouve deux troncations différentes pour l'octaèdre.
Son dessin du tétraèdre tronqué montre très explicitement comment il enlève des pyramides.
Ces polyèdres (et sept autres non dérivables des solides de Platon) ont été découverts par Archimède et décrits dans un livre aujourd'hui perdu, mais son contenu nous est connu par des écrits de Pappus d'Alexandrie. Piero est le premier à les redécouvrir et à les décrire explicitement. Ensuite Kepler a fait une étude systématique et les nomme solides d'Archimède. La contribution de Piero passe pour la postérité, une fois de plus, par le plagiat de Pacioli (et les dessins remarquables de Leonardo da Vinci utilisés par Pacioli).
Dans son texte Piero ne s'attarde pas sur la construction de ces polyèdres, mais passe rapidement aux calculs d'aires, volumes, etc.
Encore des problèmes qui, logiquement, n'ont pas leur place dans ce livre. Problèmes 10 et 11 (f.59.v - f.61.v) marquent un niveau de sophistication mathématique nettement supérieur aux autres problèmes du Libellus :
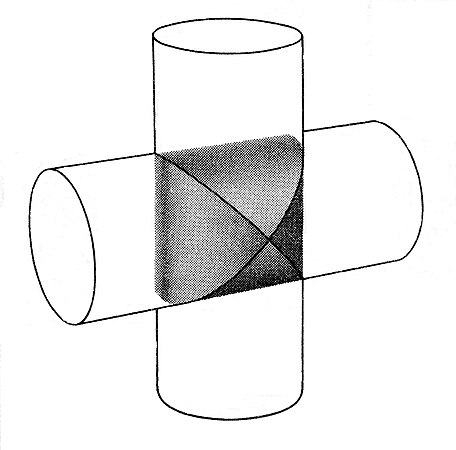
Problèmes 10 et 11 : Calculer le volume et la surface d'un voûte d'arêtes (l'intersection de deux voûtes en berceau qui sont perpendiculaires), un type de voûte très utilisé dans l'architecture depuis l'Antiquité.
Piero s'est déjà préoccupé de la représentation architecturale d'une telle voûte dans De Prospectiva pingendi. Maintenant il passe à sa représentation mathématique et le calcul habituel de volume et aire.
La description géométrique de l'objet en question est : la partie commune de l'intersection perpendiculaire de deux cylindres circulaires de même diamètre. Les solutions des problèmes 10 et 11 montrent comment calculer le volume et la surface de cet objet.
Aujourd'hui ces problèmes seraient traités comme exercices dans le calcul intégral, mais au XVe siècle le calcul intégral n'avait pas été encore découvert.
La solution de Piero montre à quel point il a assimilé et a maîtrisé les méthodes d'Archimède. Car Archimède avait considéré (et résolu) ce même problème. Piero ne pouvait pas connaître ce travail, car la méthode de solution d'Archimède était exposée dans une lettre qu'il a écrite à son ami Ératosthène. Cette lettre et d'autres écrits d'Archimède ont été conservés jusqu'au Xe siècle, puis le parchemin a été gratté, pour effacer le texte originel, et réutilisé pour écrire un livre de prières. Ce codex était conservé à Constantinople et redécouvert en 1906. Le texte originel a été (heureusement) mal effacé et on pouvait, avec l'aide de lumière ultra-violette, lire Archimède encore. Le codex est connu maintenant comme le Palimpseste d'Archimède[10]).
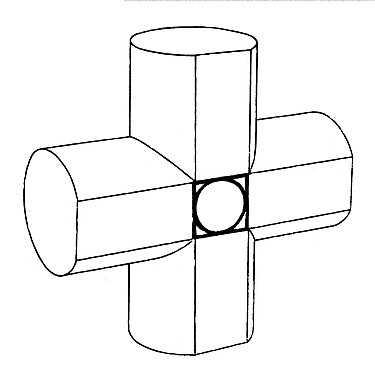
La partie du codex où Archimède donne la solution (le volume de l'objet est égal à deux tiers du volume du cube qui le circonscrit) de ce problème, De la méthode, est le seul exemplaire connu de ce traité et il est très improbable que Piero pouvait en avoir eu connaissance. Par contre, il ne faut pas oublier que Piero était imprégné par les œuvres d'Archimède (il avait fait une copie et l'illustrait avec ses propres figures) et il avait montré à plusieurs reprises qu'il était capable de redécouvrir des résultats d'Archimède. C'est certainement le cas ici, car sa méthode de solution du problème 10 diffère légèrement de celle d'Archimède et pour le problème 11, qui demande l'aire de l'objet, la question n'est pas traitée par Archimède et Piero donne la bonne solution !
La solution d'Archimède et la solution de Piero
La solution d'Archimède : dans sa lettre à Ératosthène, Archimède dit qu'il donne la démonstration, malheureusement cette parie du palimpseste n'a pas été récupérée et nous avons que le résultat final : le volume de l'objet est égal à deux tiers du volume du cube qui le circonscrit. Heureusement il existe d'autres démonstrations complètes d'Archimède de problèmes semblables qui permet une reconstruction de sa démonstration, sans grand risque d'erreur.
Soit r {\displaystyle r} 

Supposons que les cylindres et la sphère sont coupés en deux par un plan qui passe par le centre de la sphère et les deux axes des cylindres (figure A). La section de la voûte est un carré et la section de la sphère est un cercle qui remplit le carré. L'aire du cercle est π r 2 {\displaystyle \pi r^{2}} 


Imaginons maintenant une série de plans qui coupent les cylindres en fines tranches (figure B). On a toujours un carré et un cercle et le rapport entre les deux aires est toujours π 4 {\displaystyle {\frac {\pi }{4}}} 








La solution de Piero : Piero utilise également la méthode d'Archimède de couper un solide en tranches et de relier des relations entre les aires des tranches avec des relations entre les volumes des solides, mais son approche au problème est différent, avec une argumentation assez subtile.
Piero introduit la sphère qui circonscrit la voûte, comme Archimède, puis il introduit deux autres objets géométriques : un cône avec base sur la section circulaire centrale de la sphère et sommet au sommet de la voûte ; une pyramide avec base sur la section carrée centrale de la voûte et sommet, comme pour le cône, au sommet de la voûte.
D'abord Piero affirme, en citant Archimède, que le rapport des volumes du cône et l’hémisphère est 1 à 2, et que ceci implique que le rapport des volumes de la moitié de la voûte et la pyramide est également 1 à 2, donc le volume de la voûte est V = 4 4 r 3 3 = 16 3 r 3 {\displaystyle V=4{\frac {4r^{3}}{3}}={\frac {16}{3}}r^{3}} 
La justification donnée par Piero de l'affirmation (qui n'est pas évidente) sur le rapport des volumes est subtile. Il applique le raisonnement de la méthode d'Archimède deux fois : une fois en raisonnement « inverse » et une fois en raisonnement « direct ». Il y a plusieurs étapes :
La solution de Piero au problème 11 est laconique. Il affirme (correctement) que la rapport entre la surface S {\displaystyle S} 



Q.E.D.
Problème 17 : Cet exercice semble, à première vue, totalement incongru par rapport à l'esprit du traité. Piero avait développé des méthodes pour le calcul du volume de solides plus en plus compliqués et à la fin du traité, pour calculer le volume d'un solide très complexe il propose de construire un bain rectangulaire, plein d'eau, puis de mesurer le changement de niveau quand on plonge le solide dans l'eau pour calculer le volume !
Si on fait une interprétation naïve, c'est une méthode pratique (et approximative) pour mesurer le volume d'un objet. Mais si cette méthode suffit, pourquoi tous les calculs précédents ?
Piero n'avait pas l'esprit naïf, ses œuvres mathématiques, plein de subtilités et originalités, sont parfois laconiques et il n'exprime pas sa pensée profonde (comme pour le Problème 1 de la partie II). Hormis la légende qui associe Archimède avec un bain d'eau pour déterminer le volume d'une couronne d'or, le bain d'eau peut faire partie d'une « expérience de pensée ».
Si un objet a une forme si complexe que l'on ne peut pas le découper en morceaux simples, dont on peut calculer le volume, peut-on affirmer que l'objet a un volume ? Piero savait que les « nombres » 2 {\displaystyle {\sqrt {2}}} 
![{\displaystyle {\sqrt[{3}]{2}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9ca071ab504481c2bb76081aacb03f5519930710)
Le bain est aussi une illustration de la méthode utilisée dans le problème 10 : quand l'objet descend petit à petit dans l'eau, le niveau monte petit à petit et le volume d'eau qui est déplacé correspond au volume d'une fine tranche de l'objet. Le volume est la somme des volumes de ses fines tranches.
![]() : document utilisé comme source pour la rédaction de cet article.
: document utilisé comme source pour la rédaction de cet article.
 (en) Margaret Daly Davis, Piero della Francesca's Mathematical Treatises : The « Trattato d'abaco » and « Libellus de quinque corporibus regularibus », Ravenne, Longo Editore, 1977, 190 p. (Piero della Francesca's Mathematical Treatises sur Internet Archive).
(en) Margaret Daly Davis, Piero della Francesca's Mathematical Treatises : The « Trattato d'abaco » and « Libellus de quinque corporibus regularibus », Ravenne, Longo Editore, 1977, 190 p. (Piero della Francesca's Mathematical Treatises sur Internet Archive).- (it) Piero della Francesca, Libellus de quinque corporibus regularibus : Edition critique del codice Vaticano Urbenato Latino 632, Florence, Guinti, coll. « Edizione nazionale degli scritti di Piero della Francesca », 1995, 436 p. (ISBN 978-88-09-01020-8).
- (en) M.A. Lavin (dir.) et al., Piero della Francesca and His Legacy, Washington, National Gallery of Art, 1995, 328 p. (ISBN 978-0-89468-203-2).
- (en) J.V. Field (dir.), « Mathematics and the craft of painting : Piero della Francesca and Perspective », dans J.V. Field and Frank A.J.L. James, Renaissance et Revolution : Humanists, scholars, craftsmen and natural philosophers in early modern Europe, Cambridge University Press, 1997, 2e éd. (1re éd. 1993) (ISBN 0-521-43427-0, présentation en ligne).
 (en) Mark A. Peterson, « The Geometry of Piero della Francesca », sur Mount Holyoke College et (en) Mark A. Peterson, « The Geometry of Piero della Francesca », The Mathematical Intelligencer, vol. 19, no 3, juin 1997, p. 33-40 (DOI 10.1007/BF03025346, présentation en ligne).
(en) Mark A. Peterson, « The Geometry of Piero della Francesca », sur Mount Holyoke College et (en) Mark A. Peterson, « The Geometry of Piero della Francesca », The Mathematical Intelligencer, vol. 19, no 3, juin 1997, p. 33-40 (DOI 10.1007/BF03025346, présentation en ligne).- (en) James Banker, Piero della Fresca : Artist and Man, Oxford University Press, 2014, 304 p. (ISBN 978-0-19-960931-4, présentation en ligne).
- (en) Larry Witham, Piero's Light : In search of Piero della Francesca, a Renaissance painter and the revolution in Art, Science and Religion, Open Road Media, 2014, 400 p. (ISBN 978-1-60598-494-0, présentation en ligne).
↑ Il est probable que Pieri fait référence à un manuscrit De Prospectiva pingendi, mais, selon (en) James Dennistoun, Memoirs of the Dukes of Urbino, vol. 2, Londres, Longman, Brown, Green, and Longmans, 1851, 535 p. (disponible sur Internet Archive), p. 191-200, au milieu du XIXe siècle la bibliothèque des ducs d'Urbino renfermait seulement deux textes avec ce titre De Prospectiva : « MS. Urb.1374 » De Prospectiva communis de John Peckham et « MS. Urb.265 » De Perspectiva de Vitellion.
Cependant le souhaite de Piero fut accordé, car De Prospectiva pingendi manquait un titre et le catalogue de Veterano pour les manuscrits dans la bibliothèque d'Urbino a enregistré les deux œuvres comme un seul : 273 Petri Burgensis pictoris Libellus de quinque corporibus regularibus ad illustrissimum ducen Federicum et Guidonem filium est signalé par (it) C. Guasti, « Inventario della libreria urbinate complato nel secolo XV da Federigo Venterano, biblotecario de Federigo I da Montefeltro, Duca d'Urbino », Giornale storica degli archivi toscani, vol. VII, 1863, p. 55.↑ « Libellus de quinque corporibus regularibus », sur Biblioteca Apostolica Vaticana
↑ (it) Piero della Francesca, Libellus de quinque corporibus regularibus : Edition critique del codice Vaticano Urbenato Latino 632, Florence, Guinti, coll. « Edizione nazionale degli scritti di Piero della Francesca », 1995, 436 p. (ISBN 978-88-09-01020-8).
↑ (it) Luca Pacioli, Diuina proportione : opera a tutti glingegni perspicaci e curiosi necessaria oue ciascun studioso di philosophia, prospectiua, pictura sculpura, architectura, musica, e altre mathematice, suauissima, sottile, e admirabile doctrina consequira e de lectarasso co[n] varie questione de secretissima scientia, 1509, 324 p. (Diuina proportione sur Internet Archive).
↑ a et b (en) James Dennistoun, Memoirs of the Dukes of Urbino, vol. 2, Londres, Longman, Brown, Green, and Longmans, 1851, 535 p. (disponible sur Internet Archive), p. 191-200.
↑ (it) Girolamo Mancini, « L'opera «De corporibus regularibus» di Piero Franceschi detto Della Francesca usurpata da fra' Luca Pacioli », Atti della R. Accademia dei Lincei. Memorie della Classe di Scienze Morali, Storiche e Filologiche, 5e série, vol. 14, 1915, p. 441-580.
↑ (de) Max Jordan, « Der vermisste Traktat des Piero della Francesca über die fünf regelmässigen Körper », Jahrbuch der Königlich Preussischen Kunstsammlungen, vol. I, 1880, p. 112-118 (lire en ligne, consulté le 16 décembre 2018).
↑ « MS Vat. Urb.632 », sur Biblioteca Apostolica Vaticana
↑ « MS Vat. Urb.1374 », sur Biblioteca Apostolica Vaticana
↑ (en) J.J. Sylvester, « On Staudt's Theorems Concerning the Contents of Polygons and Polyhedrons, with a Note on a New and Resembling Class of Theorems », Philosophical Magazine, vol. IV, 1852, p. 335-345 (lire en ligne, consulté le 11 décembre 2018).
↑ (en) Sir Thomas Heath, The works of Archimedes, Cambridge, Cambridge, University Press, 1897, 528 p. (disponible sur Internet Archive)
(en) Sir Thomas Heath, The Method of Archimedes, recently discovered by Heiberg : a supplement to the Works of Archimedes, 1897, Cambridge, Cambridge University Press, 1912, 64 p. (disponible sur Internet Archive)
(en) E.J Dijksterhuis, Archimedes, Princeton, Princeton University Press, 1987, 457 p. (ISBN 0-691-02400-6).
- List of mathematical artists (en)
- Art et mathématiques
- Beauté mathématique
- Euclide
- Géométrie euclidienne
- Géométrie projective
- Géométrie descriptive
![]() : document utilisé comme source pour la rédaction de cet article.
: document utilisé comme source pour la rédaction de cet article.
- (en) James Banker, « Three geniuses and a franciscan friar », sur The Frick Collection (consulté le 9 septembre 2018), Vidéo d'une conférence sur Archimède, Piero della Francesca, Leonardo da Vinci et Luca Pacioli durée 60 m.
 J J O'Connor, E F Robertson et J. V. Field, « Piero della Francesca », sur MacTutor History of Mathematics archive - University of Saint-Andrews, Scotland (consulté le 9 septembre 2018).
J J O'Connor, E F Robertson et J. V. Field, « Piero della Francesca », sur MacTutor History of Mathematics archive - University of Saint-Andrews, Scotland (consulté le 9 septembre 2018).- (en) « Polyhedra & plagiarism in the Renaissance », sur Dartmouth College (consulté le 9 septembre 2018)
 Portail de la littérature italienne
Portail de la littérature italienne Portail des mathématiques
Portail des mathématiques Portail de la Renaissance
Portail de la Renaissance Portail de la langue latine
Portail de la langue latine