2018 AMS Short Course on Discrete Differential Geometry (original) (raw)
This page contains supplemental information from the AMS Short Course on Discrete Differential Geometry (DDG) held from January 8–9, 2018 in San Diego, CA. Course speakers provided an introduction to the emerging field of discrete differential geometry, which studies discrete analogs of smooth geometric objects, and provides essential links between analytical descriptions of geometry and computational algorithms. Course participants came from a variety of areas across pure & applied mathematics, ranging from undergraduate to PhD to junior and senior faculty (about 87 in all). Many thanks to our participants for making it a great event!
Course organizer: Keenan Crane (kmcrane@cs.cmu.edu)
Reading
Course Content
- Overview
[notes][slides] - Discrete Laplace Operators (Max Wardetzky)
[notes] [slides] - Discrete Parametric Surfaces (Johannes Wallner)
[notes] [slides] - Discrete Mappings (Yaron Lipman)
[notes] [slides] - Discrete Conformal Geometry (Keenan Crane)
[notes] [slides] - Discrete Optimal Transport (Justin Solomon)
[notes] [slides]
Code and Data
- Demo Session
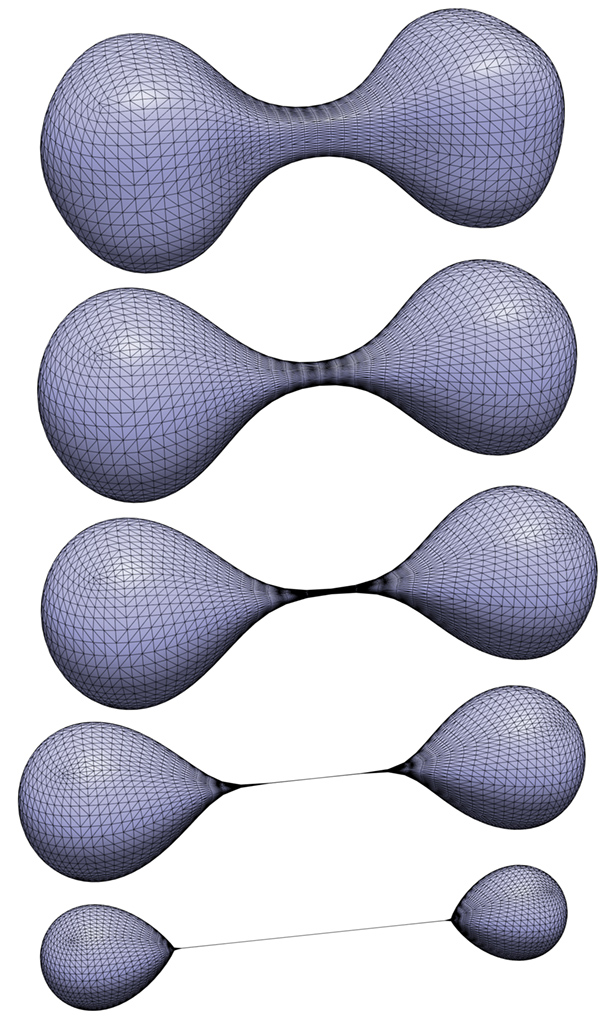
[slides] [code (JavaScript)] - <dumbbell.obj> During the interactive demo session Mike Gage suggested we run mean curvature flow on a dumbbell; we all had great fun doing a “group modeling session” where we cooked up a mesh (seek link above) and flowed it in the code:
Acknowledgements
Many thanks to Tom Barr and Lori Melucci from the AMS Short Course Subcommittee, and Joel Hass and Frank Morgan from the AMS Notices Editorial Board. Material developed for this course was sponsored in part by the National Science Foundation (Award #1717320) and the Israel Science Foundation (grant No. ISF 1830/17). Any opinions, findings, and conclusions or recommendations expressed in this material are those of the author(s) and do not necessarily reflect the views of the National Science Foundation.