Обзор методов эволюции нейронных сетей (original) (raw)

Выбор топологии и настройка весов связей искусственной нейронной сети (ИНС) являются одними из важнейших этапов при использовании нейросетевых технологий для решения практических задач. От этих этапов напрямую зависит качество (адекватность) полученной нейросетевой модели, системы управления и т.д.
Построение искусственной нейронной сети по традиционной методике выполняется, фактически, методом проб и ошибок. Исследователь задает количество слоев, нейронов, а также структуру связей между ними (наличие/отсутствие рекуррентных связей), а затем смотрит, что же у него получилось — сеть обучается с помощью какого-либо метода, а затем тестируется на тестовой выборке. Если полученные результаты работы удовлетворяют заданным критериям, то задача построения ИНС считается выполненной успешно; в противном случае — процесс повторяется с другими значениями исходных параметров.
Естественно, бурное развитие теории и практики использования генетических алгоритмов, заставило исследователей (лень — двигатель прогресса) искать способы применить их к задаче поиска оптимальной структуры ИНС (эволюция нейронных сетей или нейроэволюция), тем более, что, так сказать, proof-of-concept был налицо, или, точнее, в голове — природа наглядно демонстрировала решаемость подобной задачи на примере эволюции нервной системы с последующим образованием и развитием головного мозга.
**UPD:**Спасибо за карму :) Перенес в Искусственный интеллект.
UPD2: Переделал концевые ссылки
Сначала пара слов об авторстве. Большая часть описательного текста взято из статьи Антона Конушина [1]. Дополнительно, использовались материалы, перечисленные в конце статьи (соответствующие ссылки приведены по ходу изложения), а также результаты моих собственных изысканий.
Далее я буду исходить из предположения, что читатель знаком с концепциями ИНС и генетических алгоритмов, и опущу их описание. Желающий узнать — да погуглит или обратится к перечню источников в конце статьи. Итак, поехали.
Схемы кодирования
Как отмечают большинство исследователей, центральной точкой любого метода эволюционного построения нейронных сетей является выбор генетического представления (т.е. схемы кодирования и соответствующего декодирования). Выбор представления определяет класс сетей, которые могут быть построены с помощью данного метода. Кроме того, от них зависит эффективность метода по всем параметрам.
Общие свойства генетических представлений, по которым можно оценивать и сравнивать различные методы, выделялись многими авторами. Балакришнан и Хонаван [2] предлагают использовать следующий набор свойств: полнота, замкнутость, компактность, масштабируемость, множественность, онтогенетическая приспосабливаемость, модульность, избыточность сложность.
В этой статье я не буду более подробно останавливаться на данном перечне. Краткое описание указанных свойств можно найти в [1], а более детальное — в [2]
В настоящее время обычно выделяют два больших класса способов кодирования: прямое кодирования (direct encoding) и косвенное кодирование (indirect encoding).
В русскоязычной литературе также встречается использование терминов «параметрическое» и «непрямое» кодирование для обозначения данного класса методов. Лично мне такой перевод кажется не очень удачным, поэтому здесь и дальше я буду использовать термин «косвенное»
Прямое кодирование оперирует хромосомами, представляющими некоторое линейное представление ИНС, в котором в явном виде указаны все нейроны, веса и связи ИНС. Таким образом, всегда можно построить взаимно-однозначное соответствие между структурными элементами ИНС (нейронами, связями, весами и пр.), т.е. фенотипом, и соответствующими участками хромосомы, т.е. генотипом.
Этот способ представления нейронной сети является наиболее простым и интуитивным, а также позволяет применять к полученным хромосомам уже имеющийся аппарат генетического поиска (например, операторы кроссинговера и мутации). Из наиболее очевидных минусов такой схемы кодирования можно отметить «распухание» генотипа при увеличении количества нейронов и связей ИНС и, как следствие, низкую эффективность за счет значительного увеличения пространства поиска
Справедливости ради стоит сказать, что для прямого кодирования предложены методики, целью которых является купирование вышеописанных недостатков (например, NEAT — описанный ниже)
Косвенное кодирование (в некоторых источниках также используется термин weak — слабые, имея в виду слабосвязанные) исповедует более «биологичный» принцип — в генотипе кодируется не сам фенотип, но правила его построения (условно говоря, некая программа). При декодировании генотипа эти правила применяются в определенной последовательности (зачастую, рекурсивно и, зачастую, применимость правил зависит от текущего контекста), в результате чего и строится нейронная сеть.
При использовании косвенных методов кодирования генетическое представление (а, соответственно, и пространство поиска для генетических алгоритмов) получается более компактным, а сам генотип позволяет кодировать модульные структуры, что дает в определенных условиях преимущества в адаптивности полученных результатов. Взамен же мы получаем практическую невозможность проследить, какие изменения в генотипе привели к заданным изменениям в фенотипе, а также множество трудностей с подбором генетических операторов, сходимостью и производительностью.
Исторически, прямое кодирование было исследовано раньше и глубже, однако ряд минусов этого подхода (см. например [4]) заставляют исследователей все более пристально присматриваться к косвенным методам кодирования. Однако по своей сути косвенные методы весьма сложны для анализа. Например, одна и та же мутация правила, расположенного в начале «программы», оказывает колоссальный эффект, а примененная к «концевым» правилам — эффекта не оказывает вовсе, а в результате — генетический поиск имеет сильную тенденцию к преждевременной сходимости. Подбор операторов кроссинговера также является нетривиальной задачей, т.к. использование стандартных бинарных операторов, как правило, приводит к частому появлению нежизнеспособных решений.
Из хороших же новостей можно отметить то, что работы в области разработки методик косвенного кодирования находятся сейчас в самом разгаре, и есть место для маневра и новых открытий — так что жаждающие научной славы читатели имеют шанс попробовать себя в этой области.
Прямое кодирование
Миллер, Тодд и Хедж
В 1989 году Миллер предложил кодировать структуру нейронной сети с помощью матрицы смежности (аналогично матрице смежности для графов). Он использовал ее для записи только многослойных нейронных сетей без обратных связей. Каждой возможной прямой связи нейрона i и не входного нейрона j соответствует элемент матрицы с координатами (i,j). Если значение этого элемента равно 1, связь есть; если 0 — связи нет. Для смещений каждого нейрона выделен отдельный столбец. Таким образом, нейронной сети из N нейронов соответствует матрица размерности N * (N+1).
Геном нейронной сети по методу прямого кодирования составляется путем конкатенации двоичных строк матрицы смежности нейронной сети.
При декодировании полученного генома обратно в нейронную сеть все обратные связи (которые могут быть записаны в матрице смежности) игнорируются. Именно поэтому в такой форме записывались только нейронные сети без обратных связей. Все нейроны, к которым не ведет ни одна связь, или от которых не выходит ни одна связь удаляются.
Такое представление достаточно плохо масштабируются, т.к. длина полученного генома пропорциональна квадрату числа нейронов в сети. Поэтому его можно эффективно применять только для построения достаточно небольших по размеру нейронных сетей.
Это представление может быть использовано и для построения других классов нейронных сетей, например, с обратными связями. Для этого необходимо только внести изменения в процесс декодирования генотипа.
Анализ данного метода прямого кодирования является нетривиальной задачей. Существуют два основных вопроса:
- Какова вероятность того, что сеть будет «мертвой», т.е. входы и выходы сети вообще не соединены?
- Кодирование одной и той же структуры сети может быть выполнено множеством способов. Как узнать точно, сколько этих способов существует, и как это влияет на адаптацию в процессе генетического поиска?
Для ответа на оба этих вопроса требуется решать сложные комбинаторные задачи, и, насколько известно, исследования в этой области не проводились [5].
Стэнли, Мииккулайнен
Одной из наиболее потенциально успешных попыток избавиться от недостатков прямого кодирования с сохранением всех его достоинств является предложенный в 2002 году метод, под названием NEAT — Neural Evolution through Augmenting Topologies [6].
В своих исследованиях авторы выделили ряд ключевых проблем, свойственных прямому кодированию в частности и нейроэволюции вообще. Эти проблемы:
- Конкурирующие представления (Competing Conventions) — один и тот же фенотип (топологически) ИНС может быть по разному представлена в генотипе даже в рамках одного способа кодирования. Например — в ходе эволюции между двумя ранее созданными генами (например, А и B) был вставлен ген C, который (как это часто бывает с мутациями) на начальном этапе не несет никакой полезной информации. В результате, мы имеем особь с двумя генами (A, B) и особь с тремя генами (A, C, B). При скрещивании этих двух особей оператор кроссинговера будет применяться к генам, стоящим в соответствующих позициях (т.е. A <->A, C <-> B), что не есть очень здорово, т.к. мы начинаем скрещивать свинью (С) с апельсинами (B).
- Незащищенные инновации — при нейроэволюции инновации (т.е. изменения структуры ИНС) производятся добавлением или удалением нейронов и/или груп нейронов. И зачастую, добавление новой структуры в ИНС ведет к тому, что значение её фитнес-функции снижается. Например, добавление нового нейрона вносит нелинейность в линейный процесс, что приводит к снижению значения фитнес-функции до тех пор, пока вес добавленного нейрона не оптимизируются.
- Начальные размер и топологические инновации — во многим методиках нейроэволюции начальная популяция является набором случайных топологий. Помимо того, что приходится тратить определенное время на отсеивание изначально нежизнеспособных сетей (например, таких, у которых ни один вход не соединен ни с одним выходом), такие популяции имеют тенденцию к преждевременной сходимости к решениям, размер которых неоптимален (т.е. слишком велик). Это вызвано тем, что изначально сгенерированная случайная топология уже имеет набор связей, которые крайне неохотно редуцируются в ходе генетического поиска. Как показали эксперименты, наиболее эффективным является поиск с последовательным увеличением размера нейросети — в этом случае пространство поиска сильно сужается. Одним из способов решения этой задачи является введение штрафной функции, которая уменьшает значение фитнесс-функции в зависимости от размера сети. Однако по прежнему остается решить задачу оптимального вида этой функции, а также подбора оптимальных значений её коэффициентов.
Предложенное авторами методики решение базируется на биологическом понятии гомологичных генов (алеллей), а также на существовании в природе процесса синапсиса — выравнивания гомологичных генов перед кроссовером.
Аллели (от греч. allēlōn — друг друга, взаимно), наследственные задатки (гены), расположенные в одинаковых участках гомологичных (парных) хромосом и определяющие направление развития одного и того же признака.
В методике предполагается, что два гена (у двух разных особей) являются гомологичными, если они возникли в результате одной и той же мутации в прошлом. Другими словами, при каждой структурной мутации (добавление гена), новому гену присваивается уникальный номер (innovation number), который затем не меняется в процессе эволюции.
Использование исторических маркеров (historical markings) положено в основу решения всех трех описанных выше задач, за счет:
- Выполнения кроссовера только между гомологичными генами
- Защиты инноваций за счет введения «нишевания» — особи, имеющие близкие топологические структуры, отсеиваются, таким образом оставляя место для «новичков».
- Минимизации размерности за счет последовательного роста от минимального размера
Более подробное и полное описание методики, равно как и сравнение её с прочими методиками, приведено в [6].
Косвенное кодирование
Китано
В реальных биологических организмах генотип не является настоящим полным чертежом всей особи. Он содержит информацию о белках, т.е. об элементах, которые используются и как строительные кирпичики, из которых создается организм, и как механизмы со встроенной программой для построения других элементов организма. Такой процесс развития называется онтогенезом, и именно он вдохновил исследователей на переход к фрактальным описаниям нейронных сетей. В генотипе записывается не описание структуры нейронной сети, а программа и правила построения этой структуры.
Самый известный подход к реализации этой идеи базируется на Системах Линдемайра, или L-системах. Этот формализм был изначально грамматическим подходом к моделированию морфогенеза растений. Грамматика L-системы состоит из набора правил, использовавшихся для генерации строки-описания структуры. Процесс применения правил называется переписыванием строк (string-rewriting). К начальному символу S последовательно применяются правила переписывания строк, пока мы не получим строчку только из терминальных символов.
В 1990 году Китано разработал грамматику генерации графов (Graph Generation Grammar -GGG). Все правила имеют вид:
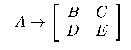
Алфавит этой грамматики содержит символы трех типов: нетерминальных N={A,B,:,Z}, предтерминальных P={a,b,:,p} и терминальных T={0,1}. Грамматика состоит из двух частей: переменной и постоянной. Переменная часть записывается в геном и состоит из последовательности описаний правил грамматики. Все символы из левой части правил должны быть нетерминальными, а из правой часть — из множества N?P. Постоянная часть грамматики содержит 16 правил для каждого предтерминального символа слева, и матрицы 2*2 из {0,1} справа. Для терминальных символов также задаются грамматические правила. Ноль раскрывается в матрицу 2*2 из нулей, а единичка — в матрицу и единиц.
При работе с такими представлениями геномов могут встречаться ситуации, когда в переменной части не задается правила для нетерминального символа, который однако использовался в правой части одного из описанных правил. Такие символы объявляются <мертвыми>, и переписываются точно так же, как нули.
Процесс декодирования состоит из последовательных применений правил из генома к начальному символу S. Количество применений правил задается в начале. Полученная матрица интерпретируется следующим образом: если на диагонали элемент (i,i)=1, то ему соответствует нейрон. Все элементы (i,j) обозначают связь нейрона i с нейроном j, если они оба существуют. Все обратные связи удаляются.
Нолфи, Париси
Нолфи и Париси предложили кодировать нейроны их координатами в двумерном пространстве. Каждая пара координат в генотипе соответствует одному нейрону. Но связи не задаются точно в генотипе, а <выращиваются> в процессе декодирования. Крайние нейроны слева считаются входными, а крайние справа — выходными.
В начале процесса декодирования все нейроны помещаются на плоскости в точках, заданных их координатами. Затем они индексируются. Индекс скрытых нейронов определяется их координатой х. Если у двух нейронов их х-овые координаты совпадают, то больший номер получает тот нейрон, который был считан из генома позже (д.е. закодирован дальше, чем другой). Индексы всех входных и выходных нейронов рассчитываются иначе. Каждому нейрону в генотипе также соответствует параметр тип. Для входных нейронов индекс равен I = type mod N(input), а для выходных нейронов он рассчитывается по формуле j = N — N(output) + type mod N(output). Где N(input) — количество входов в нейронную сеть, N(output) — количество выходов из нейронной сети. Очевидно, что некоторые входные и выходные нейроны будут иметь один и тот же индекс. Поэтому, при декодировании к нейронной сети добавляется N(input) входных и N(output) выходных реальных нейронов, к которым присоединены входы и выходы сети. Каждый такой дополнительный нейрон связывается со всеми нейронами с соответствующим индексом.
После декодирования всех нейронов и размещения их в пространстве, из каждого нейрона начинает строиться дерево связей. Обычно оно рассчитывается как фрактал, но конкретный метод его вычисления не важен. Длины сегментов-ветвей дерева, и угол между ветвями задается при описании каждого нейрона в геноме. Связь между нейронами устанавливается, если одна из ветвей графа подход к другому нейрону меньше, чем на установленной заранее пороговое значение.
Изначально обучение записанных таким образом сетей отдельно не проводилось, они эволюционировали вместе с весовыми коэффициентами, которые также записывались в геном. Но подобное представление может применяться и исключительно для построения структуры сети, а веса могут рассчитываться и по стандартным алгоритмам.
Кангелосси, Париси и Нолфи
Этот метод с одной стороны является развитием предыдущего, а с другой — использует фрактальный порождающий процесс, аналогичный грамматическому представлению.
Этот подход был разработан Кангелоси, Париси и Нолфи. Вместо того, чтобы кодировать каждый нейрон напрямую, они записывают набор правил для разделения и смещения нейронов. Поэтому метод получил название порождающего пространства из ячеек (Generative cell space GCS).
Процесс онтогенеза начинается с одной клетки — <яйца> специального типа. Эта клетка затем разделяется (<переписывается>) в две дочерние клетки, причем параметры разделения задаются в правиле. Каждая из клеток-потомков могут быть размещены в одной из 8-и соседних с родительской клетках. Процесс повторяется заданное число раз, после чего все построенные клетки <взрослеют> и превращаются в нейроны. Они разделяются на входные, выходные и скрытые по тому же принципу, что и в предыдущем методе.
Кангелосси и Элман
Этот метод является более биологичным развитием предыдущего. Он использует т.н. genetic regulation network (GRN) для контроля процесса построения сети. Их GRN состоит из 26 регулирующих элементов (генов), построенных по аналогии с биологическими оперонами. Каждый оперон разделен на две части — регуляторную (regulatory) и экспрессивную (expression). Регуляторная часть состоит из двух регионов: индуктор и ингибитор. Экспрессивная часть также состоит из двух регионов: регуляторный и структурный. Если регуляторный регион гена совпадает с индуктором другого гена, последний экспрессируется (т.е. выполняются команды, заданные в его структурной части). Экспрессия происходит если она не была запрещена ингибитором другого гена. Количество экспрессируемого гена («количество получаемых химических элементов») зависит от индукторной части регуляционного элемента.
О'Нил и Брабазон
Предложенный авторами метод основан на методе формальных грамматик. Однако формальная грамматика, используемая для построения последовательности комманд, в свою очередь описывается некоторой мета-грамматикой.
Например, нижеуказанная универсальная или мета-грамматика позволяет генерировать произвольный 8-битовые последовательности:
::= " ::=" " ::=" " ::="
" ::=" " ::=" ::=
::= ::= ::= | "|"
::= "" | "" | ""
::= "" | 1 | 0 ::= | "|"
::= 1 | 0
Для трансляции грамматики используется входная битовая строка, которая указывает последовательность номеров правил, выбираемых в тех случаях, когда нетерминал содержит более одного способа вывода.
Например, вышеописанная мета-грамматика, может породить следующую грамматику:
::= 1100
| | 11011101 | | ::= 11
::= 11 ::= 1 ::= 1 | 0 | 0 | 1
Таким образом, генотип особи представляет собой две бинарных строки — одна предназначена для генерации грамматики на основе мета-грамматики, а другая — для генерации уже, собственно, ИНС на основе полученной грамматики.
Более подробно описание метода см. в [7], [8]
Прочие методики
Существует множество прочих методик нейроэволюции (часть из которых в [5]). здесь я приведу только краткие описания каждой из них:
- Боерс и Куйпер (Boers and Kuiper) — использование контексто-зависимых L-систем
- Дилаерт и Бир (Dellaert and Beer) — подход, аналогичный Кангелосси и Элману, но с использованием случайных булевых нейросетей (random boolean networks)
- Харп, Самад и Гуха (Harp, Samad, and Guha) — позонное прямое кодирование структуры
- Груау (Gruau) — использование грамматического дерева для задания инструкций при делении клеток (чем-то похоже на Кангелосси, Париси и Нолфи)
- Ваарио (Vaario) — рост клеток задается L-системами
Сравнение различных подходов к нейроэволюции
К сожалению, однозначно сказать, какой из вышеописанных подходов является наиболее оптимальным, в настоящее время довольно затруднительно. Это связано с тем, что однозначного критерия «универсальной оценки» так и не выработано. Как правило и сами авторы, и сторонние исследователи оценивают эффективность на основе тех или иных тестовых задач в рамках определенных проблемных областей, и при этом трактуют результаты очень по разному. Более того, практически во всех встреченных мне сравнительных работах делаются оговорки насчет того, что полученные результаты могут измениться при изменении тестовых условий и что требуются дополнительные исследования (каковую оговорку делаю и я).
Исключительно в ознакомительных целях привожу краткие результаты сравнений, выполненных в [5] (сравниваются ряд алгоритмов между собой) и в [6] (сравнивается методика NEAT с некоторыми другими методиками).
В [5] выполнялось сравнение следующих методик
- Миллер (прямое кодирование)
- Китано (кодирование на L-системах)
- Нолфи (пространство ячеек)
- Кангелоси (порождающее пространство ячеек)
Для сравнения использован ряд искусственных и жизненных проблем на которых и проводилось сравнение.
Детальные результаты приведены в [5], однако в общем можно отметить, что:
- Сети, эволюционированные по методу Китано дают лучшие результаты
- Сети, построенные по методу Миллера не сильно хуже Китано
- Сети, построенные по методу Нолфи заметно хуже Китано и Миллера
- Сети, построенные по методу Кангелосси еще хуже Нолфи.
Впрочем, отмечается, что лучшие сети построенные с помощью двух «плохих» методов (Нолфи и Кангелосси) демонстрируют заметно больший потенциал к обучаемости в тех случаях, когда они обучаются несколько раз с различными случайными начальными весами.
В [6] выполняется сравнение NEAT с некоторыми другими методиками (эволюционное программирование [7], conventional neuroevolution [8], Sane [9], и ESP [10]). Результаты сравнения на одной из задач (балансирование двуми жердями — детали см. в [11]) приведены в таблице.
| Method | Evaluations | Generations | No. Nets |
|---|---|---|---|
| Ev. Programming 307,200 150 2048 | 307,200 | 150 | 2048 |
| Conventional NE | 80,000 | 800 | 100 |
| SANE | 12,600 | 63 | 200 |
| ESP | 3,800 | 19 | 200 |
| NEAT | 3,600 | 24 | 150 |
Как можно увидеть, NEAT ведет себя значительно лучше, чем большинство сравниваемых методик (неудивительно, учитывая, что данные были опубликованы авторами методики), однако, опять же, эти данные требуют проверки в прочих проблемных областях.
Вместо заключения [3]
Совместное использование эволюционных алгоритмов и ИНС позволяет решать задачи настройки и обучения ИНС как по отдельности, так и одновременно. Одним из достоинств такого синтезированного подхода является во многом унифицированный подход к решению разнообразных задач классификации, аппроксимации, управления и моделирования. Использование качественной оценки функционирования ИНС позволяет применять нейроэволюционные алгоритмы для решения задач исследования адаптивного поведения интеллектуальных агентов, поиска игровых стратегий, обработки сигналов. Несмотря на то, что количество проблем и открытых вопросов, касающихся разработки и применения НЭ алгоритмов (способы кодирования, генетические операторы, методы анализа и др.) велико, часто для успешного решения задачи с использованием НЭ алгоритма достаточно адекватного понимания проблемы и НЭ подхода, свидетельством чего является большое число интересных и успешных работ в данном направлении.
[1] — Эволюционные нейросетевые модели с незаданным заранее числом связей
[2] — Properties of genetic representations of neural architectures (1995, Karthik Balakrishnan, Vasant Honavar)
[3] — Эволюционный подход к настройке и обучению искусственных нейронных сетей (2006, Цой Ю.Р., Спицын В.Г.)
[4] — Evolving Neural Networks (2009, Risto Miikkulainen and Kenneth O. Stanley)
[5] — Evolutionary Design of Neural Networks (1998, Marko A. Gronroos)
[6] — Evolving Neural Networks through Augmenting Topologies (2002, K. O. Stanley and R. Miikkulainen)
[7] — Evolving neural control systems (1995, Saravanan, N. and Fogel, D. B.)
[8] — Evolving neural network controllers for unstable systems (1991, Wieland, A.)
[9] — SANE
[10] — Learning robust nonlinear control with neuroevolution (2002, Gomez, F. and Miikkulainen, R.)
[11] — Pole Balance Tutorial