Interpreter Design Pattern - Lukasz Wrobel (original) (raw)
When thinking of parsing math expressions (which can be thought of as kind of language interpretation), one should not give the Interpreter Pattern a miss.
Interpreter is one of the design patterns originally described by the “Gang of Four”. It refers to interpreting some abstract language and it shows one of the ways of building an interpreter.
The keynote is simple: write a class for each kind of symbol that may occur in expression, then instantiate those classes and connect the objects together so they will form a tree. What does it mean in practice? I’ll try to show this on the example of math expressions written in the Reverse Polish notation.
Define Classes
First, we have to think what classes are we going to need. Since we’re going to build a math expression parser, the following classes should come in handy:
-3,5,12.41etc. - aNumberclass+- aPlusclass-- aMinusclass*- aMultiplyclass
This should be enough for the moment. Let’s write these classes now, each of them should contain an execute() method responsible for interpreting its subpart of the expression. I decided not to declare any superclass - the interpreter is going to be written in Ruby and I think duck typing may be turned into good use in a small project like this one.
# Author:: Lukasz Wrobel
# Url:: http://lukaszwrobel.pl/
class Number
def initialize(value)
@value = value
end
def execute
@value
end
end
class Plus
def initialize(left, right)
@left = left
@right = right
end
def execute
@left.execute + @right.execute
end
end
class Minus
def initialize(left, right)
@left = left
@right = right
end
def execute
@left.execute - @right.execute
end
end
class Multiply
def initialize(left, right)
@left = left
@right = right
end
def execute
@left.execute * @right.execute
end
end
The Number class (representing a terminal symbol) requires only a simple value in order to be initialized. However, the rest of the classes above require class instances, which can represent arbitrarily complex expressions.
For example, left and right in the Multiply class can be both numbers, or one of them can be a number and the other may represent a complex sum. The Multiply object doesn’t care, though - it just passes through an execute() message to both of its arguments and then multiplies partial results. It’s all about delegation.
Wait a minute… We have an expression, we’ve defined classes and what we don’t know is how to turn the expression into a tree. We need a parser!
Write a Parser
Our goal is to build an abstract syntax tree (AST). This tree will be an object representation of the math expression. Let’s take a look at an example:
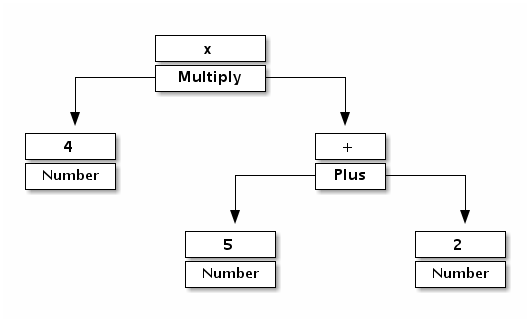
Every node of the tree represents a symbol, either terminal or nonterminal. Moreover, every node is an instance of appropriate class, which knows how to evaluate itself. A Number instance returns its value, a Multiply instance multiplies its arguments etc. The tree can grow in size and become really complex.
By the way, the AST tree used in Interpreter is an instance of another design pattern, called Composite. Why? Because each node is treated the same way, regardless whether it is a number or a complicated operator which requires to evaluate its arguments and perform some complicated operations. Client deal with a single number in exactly the same way as it does with a complex expression - it just runs the execute() method and don’t care about the details. This is what we call a Composite.
Let’s get back to work and write the parse() function which builds a tree and initiates the evaluation process:
# Author:: Lukasz Wrobel
# Url:: http://lukaszwrobel.pl/
def parse(input)
stack = []
input.lstrip!
while input.length > 0
case input
when /\A-?\d+(\.\d+)?/
stack << Number.new($&.to_i)
else
second, first = stack.pop(), stack.pop()
case input
when /\A\+/
stack << Plus.new(first, second)
when /\A\-/
stack << Minus.new(first, second)
when /\A\*/
stack << Multiply.new(first, second)
else
raise 'Token unknown'
end
end
input = $'
input.lstrip!
end
raise 'Syntax error' unless stack.size == 1
stack.first.execute
end
This function can be used like this:
parse('4 5 2 + *')
=> 28
Of course, the parse() function can be further modularized, e.g. by being put into a class. But for the test purposes it will do just fine.
The input string is being read from left to right and each token is being recognized. It can be either a number or an operator (+, -, *). If the parser encounters an operator, it pops the arguments from the stack and passes them to the operator instance.
At the end of the parsing process, there should be only one element left on the stack. It’s the root of the Abstract Syntax Tree (in case of the example image, it’s the Multiply node on the top). If stack size is different than one, it means that input expression is empty or that the expression is not valid.
When the parsing is done, the evaluation process is then being initialized by running the execute() method on the root of the Abstract Syntax Tree. Client is given the result or - if something went wrong - an exception, which should be properly handled.
Taking Advantage of the Interpreter Pattern
It seems that our parser simply works (we should add some tests, however). But the solutions we’ve just discussed has at least two disadvantages when compared to a smart Reverse Polish notation parser I’ve talked about before. The version with Interpreter requires some additional code (i.e., classes to handle each operator type) and it adds overhead because of creating many objects instances, even for such simple structures as numbers.
That’s all true. Imagine, however, that the Interpreter design pattern not only adds overhead, it also gives you some additional possibilities. For example, imagine that the expression contains not only numbers and operators, but also variables. Expression value may vary according to values assigned to variables.
When using a traditional parser, the expression would have to be parsed each time the variables values are changed. With the Interpreter pattern, the situation is much more comfortable. Once the Abstract Syntax Tree is built, it may be reused many times. All you have to do is to provide the interpreter with up-to-date variables values. Remember - current conditions in which the interpreter is working (e.g. variables values) are called a context. Replace the context, keep the syntax tree and spare CPU cycles.
Other Applications
By using the Interpreter design pattern to parse RPN expressions, we didn’t make a revolution. Take into account, though, that some applications of the Interpreter have made a big and well-deserved career. The Interpreter is being used to evaluate expressions written in highly specialized languages, like SQL (Structured Query Language).
I’m sure you’ve encountered such situations in your programming career when expressing operations and dependencies in the programming language of your choice seemed unnatural and required writing similar code many times and spreading it across the source code. To accomplish such a complicated task like selecting all data from a database table, all you need to write is:
SELECT * FROM `my_table`;
Pretty straightforward, isn’t it? Achieving the same result in embedded SQL would require writing at least a few additional lines of code.
DSL - One Step Further
There is a design pattern, called DSL (Domain-Specific Language), which can be considered as an extension of the Interpreter pattern. There are many examples of DSLs, like various Wiki markup languages. I think that DSL implementation in Ruby is interesting enough to deserve a separate article.
It seems that’s all you should know about the Interpreter design pattern. Remember about it next time you’ll be tempted to create your own simple language in order to solve some specialized problem. The Interpreter might be a good choice!