Disdyakis Triacontahedron (original) (raw)
Algebra Applied Mathematics Calculus and Analysis Discrete Mathematics Foundations of Mathematics Geometry History and Terminology Number Theory Probability and Statistics Recreational Mathematics Topology
Alphabetical Index New in MathWorld

The disdyakis triacontahedron is the dual polyhedron of the Archimedean great rhombicosidodecahedron. It is also known as the hexakis icosahedron (Holden 1971, p. 55). It is illustrated above together with a wireframe version and a net that can be used for its construction.
It is Wenninger dual 
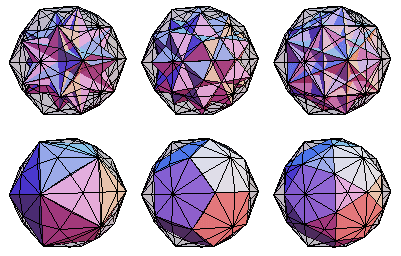
A tetrahedron 10-compound, octahedron 5-compound, cube 5-compound, icosahedron,dodecahedron, and icosidodecahedron can be inscribed in the vertices of a disdyakis triacontahedron (E. Weisstein, Dec. 26-27, 2009).
Starting with an Archimedean great rhombicosidodecahedron of unit edge lengths, the edge lengths of the corresponding disdyakis triacontahedron are
The corresponding midradius is
 |
(4) |
|---|
The surface area and volume are
See also
Archimedean Dual, Archimedean Solid, Disdyakis Triacontahedral Graph
Explore with Wolfram|Alpha
References
Holden, A. Shapes, Space, and Symmetry. New York: Columbia University Press, p. 55, 1971.Kabai, S. Mathematical Graphics I: Lessons in Computer Graphics Using Mathematica. Püspökladány, Hungary: Uniconstant, p. 141, 2002.Wenninger, M. J. Dual Models. Cambridge, England: Cambridge University Press, pp. 25 and 27, 1983.
Cite this as:
Weisstein, Eric W. "Disdyakis Triacontahedron." From MathWorld--A Wolfram Web Resource. https://mathworld.wolfram.com/DisdyakisTriacontahedron.html