Quadrilateral (original) (raw)

Algebra Applied Mathematics Calculus and Analysis Discrete Mathematics Foundations of Mathematics Geometry History and Terminology Number Theory Probability and Statistics Recreational Mathematics Topology

Alphabetical Index New in MathWorld

Quadrilateral

A quadrilateral, sometimes also known as a tetragon or quadrangle (Johnson 1929, p. 61) is a four-sided polygon. If not explicitly stated, all four polygon vertices are generally taken to lie in a plane. (If the points do not lie in aplane, the quadrilateral is called a skew quadrilateral.) There are three topological types of quadrilaterals (Wenninger 1983, p. 50): convex quadrilaterals (left figure), concave quadrilaterals (middle figure), and crossed quadrilaterals (or butterflies, or bow-ties; right figure).

A quadrilateral with two sides parallel is called a trapezoid, whereas a quadrilateral with opposite pairs of sides parallel is called a parallelogram.

QuadrilateralVectors

For a planar convex quadrilateral (left figure above), let the lengths of the sides be a, b, c, and d, the semiperimeter s, and the polygon diagonals p and q. The polygon diagonals are perpendicular iff a^2+c^2=b^2+d^2.

An equation for the sum of the squares of side lengths is

a^2+b^2+c^2+d^2=p^2+q^2+4x^2, (1)

where x is the length of the line joining the midpoints of thepolygon diagonals (Casey 1888, p. 22).

For bicentric quadrilaterals, the circumcircleand incircle satisfy

2r^2(R^2-s^2)=(R^2-s^2)^2-4r^2s^2, (2)

where R is the circumradius, r in the inradius, and s is the separation of centers.

Given any five points in the plane in general position, four will form a convex quadrilateral. This result is a special case of the so-called happy end problem (Hoffman 1998, pp. 74-78).

There is a beautiful formula for the area of a planar convex quadrilateral in terms of the vectors corresponding to its two diagonals. Represent the sides of the quadrilateral by the vectors a,b, c, and d arranged such that a+b+c+d=0 and the diagonals by the vectors p and q arranged so that p=b+c and q=a+b. Then

where det(A) is the determinant and pxq is a two-dimensional cross product.

There are a number of beautiful formulas for the area of a planar convex quadrilateral in terms of the side and diagonal lengths, including

(Beyer 1987, p. 123), Bretschneider's formula

(Coolidge 1939; Ivanoff 1960; Beyer 1987, p. 123) where s is the semiperimeter, and the beautiful formula

K=sqrt((s-a)(s-b)(s-c)(s-d)-abcdcos^2[1/2(A+B)]) (9)

(Bretschneider 1842; Strehlke 1842; Coolidge 1939; Beyer 1987, p. 123).

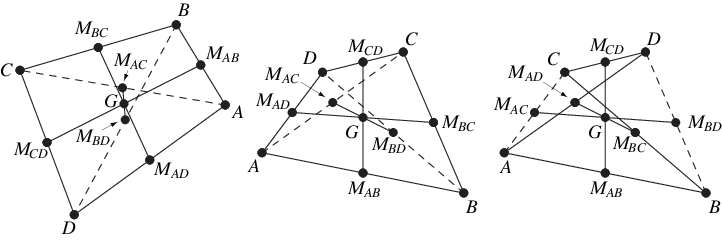
QuadrilateralCentroid

The centroid of the vertices of a quadrilateral occurs at the point of intersection of the bimedians (i.e., the lines M_(AB)M_(CD) and M_(AD)M_(BC) joining pairs of opposite midpoints) (Honsberger 1995, pp. 36-37). In addition, it is the midpoint of the line M_(AC)M_(BD) connecting the midpoints of the diagonals AC and BD (Honsberger 1995, pp. 39-40).

QuadrilateralBisectors

The four angle bisectors of a quadrilateral intersect adjacent bisectors in four concyclic points (Honsberger 1995, p. 35).

QuadrilateralTiling

Any non-self-intersecting quadrilateral tiles the plane.

There is a relationship between the six distances d_(12), d_(13), d_(14), d_(23), d_(24), and d_(34) between the four points of a quadrilateral (Weinberg 1972):

0=d_(12)^4d_(34)^2+d_(13)^4d_(24)^2+d_(14)^4d_(23)^2+d_(23)^4d_(14)^2+d_(24)^4d_(13)^2+d_(34)^4d_(12)^2+d_(12)^2d_(23)^2d_(31)^2+d_(12)^2d_(24)^2d_(41)^2+d_(13)^2d_(34)^2d_(41)^2+d_(23)^2d_(34)^2d_(42)^2-d_(12)^2d_(23)^2d_(34)^2-d_(13)^2d_(32)^2d_(24)^2-d_(12)^2d_(24)^2d_(43)^2-d_(14)^2d_(42)^2d_(23)^2-d_(13)^2d_(34)^2d_(42)^2-d_(14)^2d_(43)^2d_(32)^2-d_(23)^2d_(31)^2d_(14)^2-d_(21)^2d_(13)^2d_(34)^2-d_(24)^2d_(41)^2d_(13)^2-d_(21)^2d_(14)^2d_(43)^2-d_(31)^2d_(12)^2d_(24)^2-d_(32)^2d_(21)^2d_(14)^2. (10)

This can be most simply derived by setting the left side of the Cayley-Menger determinant

| 288V^2=\|0 1 1 1 1; 1 0 d_(12)^2 d_(13)^2 d_(14)^2; 1 d_(21)^2 0 d_(23)^2 d_(24)^2; 1 d_(31)^2 d_(32)^2 0 d_(34)^2; 1 d_(41)^2 d_(42)^2 d_(43)^2 0| | (11) | | ------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------- | ---- |

equal to 0 (corresponding to a tetrahedron of volume 0), thus giving a relationship between the distances between vertices of a planar quadrilateral (Uspensky 1948, p. 256).

A special type of quadrilateral is the cyclic quadrilateral, for which a circle can be circumscribed so that it touches each polygon vertex. Another special type is a tangential quadrilateral, for which a circle and be inscribed so it is tangent to each edge. A quadrilateral that is both cyclic and tangential is called a bicentric quadrilateral.

See also

Anticenter, Bicentric Quadrilateral, Bimedian, Brahmagupta's Formula, Bretschneider's Formula, Butterfly Theorem, Cayley-Menger Determinant, Complete Quadrilateral,Cyclic Quadrilateral, Diamond,Eight-Point Circle Theorem, Equilic Quadrilateral, Fano's Axiom, Léon Anne's Theorem, Lozenge, Maltitude,Orthocentric Quadrilateral, Parallelogram,Ptolemy's Theorem, Rational Quadrilateral, Rectangle, Rhombus,Skew Quadrilateral, Square,Tangential Quadrilateral, Trapezoid,van Aubel's Theorem, Varignon's Theorem, Wittenbauer's Parallelogram Explore this topic in the MathWorld classroom

Explore with Wolfram|Alpha

References

Beyer, W. H. (Ed.). CRC Standard Mathematical Tables, 28th ed. Boca Raton, FL: CRC Press, p. 123, 1987.Bretschneider, C. A. "Untersuchung der trigonometrischen Relationen des geradlinigen Viereckes." Archiv der Math. 2, 225-261, 1842.Casey, J. A Sequel to the First Six Books of the Elements of Euclid, Containing an Easy Introduction to Modern Geometry with Numerous Examples, 5th ed., rev. enl. Dublin: Hodges, Figgis, & Co., 1888.Coolidge, J. L. "A Historically Interesting Formula for the Area of a Quadrilateral." Amer. Math. Monthly 46, 345-347, 1939.Dostor, G. "Propriétés nouvelle du quadrilatère en général...." Archiv d. Math. u. Phys. 48, 245-348, 1868.Durell, C. V. "The Quadrilateral and Quadrangle." Ch. 7 in Modern Geometry: The Straight Line and Circle. London: Macmillan, pp. 77-87, 1928.Fukagawa, H. and Pedoe, D. "Circles and Quadrilaterals" and "Quadrilaterals." §3.5 and 4.2 in Japanese Temple Geometry Problems. Winnipeg, Manitoba, Canada: Charles Babbage Research Foundation, pp. 43-45, 47-48, and 125-132, 1989.Harris, J. W. and Stocker, H. "Quadrilaterals." §3.6 in Handbook of Mathematics and Computational Science. New York:Springer-Verlag, pp. 82-86, 1998.Hobson, E. W. A Treatise on Plane and Advanced Trigonometry. New York: Dover, pp. 204-205, 1957.Hoffman, P. The Man Who Loved Only Numbers: The Story of Paul Erdős and the Search for Mathematical Truth. New York: Hyperion, 1998.Honsberger, R. "On Quadrilaterals." Ch. 4 in Episodes in Nineteenth and Twentieth Century Euclidean Geometry. Washington, DC: Math. Assoc. Amer., pp. 35-41, 1995.Ivanoff, V. F. "Solution to Problem E1376: Bretschneider's Formula." Amer. Math. Monthly 67, 291-292, 1960.Johnson, R. A. "Quadrangles and Quadrilaterals" and "The Theorem of Ptolemy." §91-92 in Modern Geometry: An Elementary Treatise on the Geometry of the Triangle and the Circle. Boston, MA: Houghton Mifflin, pp. 61-64, 1929.Routh, E. J. "Moment of Inertia of a Quadrilateral." Quart. J. Pure Appl. Math. 11, 109-110, 1871.Strehlke, F. "Zwei neue Sätze vom ebenen und shparischen Viereck und Umkehrung des Ptolemaischen Lehrsatzes." Archiv der Math. 2, 33-326, 1842.Uspensky, J. V. Theory of Equations. New York: McGraw-Hill, p. 256, 1948.Weinberg, S. Gravitation and Cosmology: Principles and Applications of the General Theory of Relativity. New York: Wiley, p. 7, 1972.Wenninger, M. J. Dual Models. Cambridge, England: Cambridge University Press, 1983.

Referenced on Wolfram|Alpha

Quadrilateral

Cite this as:

Weisstein, Eric W. "Quadrilateral." FromMathWorld--A Wolfram Web Resource. https://mathworld.wolfram.com/Quadrilateral.html

Subject classifications