Ferrite Transformer Turns Calculation with Example (original) (raw)

In this article, you will learn how to calculate the turns ratio of a ferrite core transformer for high-frequency switch mode power supply inverters. High-frequency ferrite core transformers are used in almost every power electronics circuit, such as inverters and pure sine wave inverters. They are used to boost up or step up the low DC voltage of a battery and other DC sources, like solar panels. Ferrite core transformers are also used in isolated DC to DC converters to step down or step up the DC voltage. For example, in an isolated buck converter, it is used to step down the DC voltage, and in an isolated boost converter, they are used to step up the DC voltage. In this article, we will learn how to calculate the turns ratio of a high-frequency ferrite core transformer with examples.

What is Ferrite Core Transformer?

A Ferrite Core Transformer is a type of transformer that uses a ferrite core instead of an iron core. Ferrite cores are made from a mixture of iron oxide and other metals, and they have unique magnetic properties that make them suitable for use in high-frequency applications. Ferrite core transformers are commonly used in power electronics circuits, such as inverters and DC to DC converters, to step up or step down voltage levels. They are known for their high efficiency and compact size, making them ideal for applications where space and energy efficiency are important.

Ferrite Core Turns Ratio Calculation

For example, in the boost-up stage we have two options to choose from in power electronics converters: push-pull topology and full bridge. I will explain both methods one by one. The turns ratio calculation formula and concept remain the same for both topologies. The only difference between the push-pull topology and the full bridge transformer design is that the push-pull ferrite core transformer requires a center tap in the primary winding. In other words, the push-pull transformer has twice the number of primary turns than the full bridge transformer.

Push-pull topology ferrite core turns ratio calculation with examples

Let’s start with an example. For example, we want to design a 250-watt boost-up DC-to-DC converter. We are using push-pull topology for this design. We are using a 12-volt battery and we want to step up the DC voltage from 12 volts to 310 volts. The switching frequency of the design is 50 kHz. We are using an ETD39 ferrite core which can handle 250 watts. It is beyond the scope of this topic to explain how to select a ferrite core according to the power rating. I will try to write a separate article on it. The output of the ferrite core will always be a high-frequency square wave of 50 kHz. We need to use a full rectifier to convert it into a DC voltage of 310 volts. You may also need to use an LC filter to remove harmonics or AC components from the output.

Ferrite Transformer Turns Calculation

Ferrite Transformer Primary Turns Calculation

As you know, battery voltage does not remain the same all the time. As the load on the battery increases, the battery voltage will be less than 12 volts. With no load and a fully charged battery, the battery voltage will be near 13.5 volts. Therefore, the input voltage is not constant, and we must consider it while calculating the turns ratio of the ferrite core transformer. The cutoff voltage for the battery is usually 10.5 volts. We can take it as the smallest possible value of the input voltage to boost up the DC converter. So, we have the following parameters now:

Vinput = 10.5 volt

Vout = 310 volt

As we know that formula of turns ratio calculation in transformer is

N = Npri / Nsc = Vin / Vout

Where Npri is the number of primary turns and Nsc is the number of secondary turns. We have three known variables like turns ratio, which can be calculated by the above equation, input voltage, and output voltage. But we need to calculate the primary turns to find the secondary turn of a ferrite core transformer. The formula to calculate the primary turns for a ferrite core transformer is given below:

Npri = Vin * 10^8 / 4 * f * Bmax * Ac

But for push-pull, it will be half the number of turns compared to the primary.

Where Npi is the primary number of turns, Vin(nom) is the normal input voltage which, in our example, is 10.5 volts.
Bmax is the maximum flux density. The unit of maximum flux density is Gauss. Remember, if you are using Tesla as the unit for maximum flux density, Bmax = 10^4 Gauss. The value of maximum flux density is usually given in the data sheet of the ferrite core. We usually take the value of Bmax between 1300G to 2000G. This is usually an acceptable range for all ferrite core transformers. Note: A high value of flux density will saturate the core, and a low value of flux density will lead to underutilization of the core. For example, we will take 1500G for the DC to DC converter.
f is the switching frequency of the converter. In our example, the switching frequency of the DC to DC converter is 50 kHz.
Ac is the effective cross-sectional area of the ferrite core. We have to refer to the data sheet for this value. In this example, we are using the ETD39 core. The effective cross-sectional area of the ETD39 is 125 mm^2 or 1.25 cm^2.

We have all the values to calculate primary number of turns .i.e.

Vin = 10.5 volt, Bmax = 1500G, f = 50 KHz, Ac = 1.25 cm^2

By putting these parameters in two above formula, we can calculate turns primary number of turns.

Npri = 12 . 10^8 / 4 . 50000 . 1500 . 1.25 = 3.2

Hence Npri = 3.2, but we cannot use fractional turns. So we need to round off the calculated value of primary turns to the nearest whole number, which is 3. The primary number of turns for the ferrite core is 3. However, before that, we need to check whether for Npri = 3, Bmax is within the acceptable range or not. As mentioned above, the acceptable range for Bmax is 1300-2000G. But the question is, why do we need to check the value of Bmax again? This is because we adjusted the value of primary turns from 3.2 to 3. So let’s calculate the value of Bmax for Npri = 3 using the above formula.

Bmax = Vin * 10^8 / 4 * f * Npri * Ac

Bmax = 12 * 10^8 / 5 * 50000 * 3 * 1.25 = 1600G

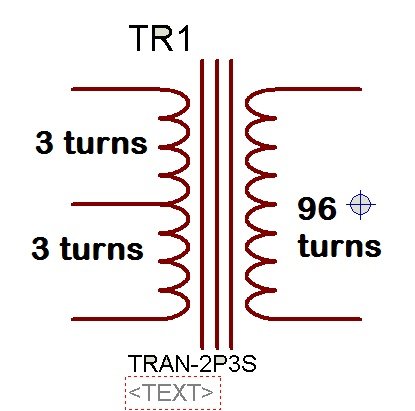
So the calculated value of Bmax is 1600G, which is within the acceptable range of the maximum flux density. This means we can take Npri = 3 for further calculations. The primary number of turns for the push-pull ferrite center-tap transformer is 3 turns + 3 turns. In any design, you will need to adjust the value of Npri if it is in fraction. You can easily adjust it. But you need to check the value of Bmax every time. We start with an assumed value of Bmax and calculate Npri. But you can also start with an assumed value of Npri and check the value of the maximum flux density Bmax. For example, suppose a value of Npri = 1 and check the value of Bmax, and keep repeating this process until it falls within an acceptable range.

Ferrite Transformer Secondary Turns Calculation

Now let’s move to the secondary turn of the ferrite core. In our design, the output of the DC to DC converter is 310 volts at any input voltage. The input voltage is variable from 10.5 volts to 13.5 volts. We will need to implement feedback to regulate the output voltage to 310 volts. Therefore, we will use a slightly higher value for the output voltage so that even at the minimum input voltage, we can still achieve an output voltage of 310 volts by adjusting the duty cycle of the PWM. So, we should design a ferrite core transformer with a secondary rated at 330 volts. The feedback mechanism will dynamically adjust the output voltage by varying the duty cycle of the PWM. Additionally, you should consider losses and voltage drops across switching devices while designing the transformer.

So, the transformer must be able to supply a 330-volt output with an input range of 13.5 volts to 10.5 volts. The maximum duty cycle for PWM is 98%, leaving the remaining 2% for dead time. During the minimum possible input voltage, the duty cycle will be at its maximum. At a maximum duty cycle of 98%, the input voltage to the transformer is 0.98 * 10.5 = 10.29 volts.

By using voltage ratio formula of transformer = voltage ratio = 330 / 10.29 = 32.1. Voltage ratio and turns ratio in transformer is equal to each other. Hence N = 32.

So we know all values to calculate secondary turns of ferrite core transformer.

N = 32, Npri = 3

Nsec = N * Npri = 32 *3 = 96

So the number of primary turns is equal to 3, and the number of secondary turns is equal to 96. This is all about the turns ratio calculation for high-frequency transformers. If you have any issues, please let me know in the comments.