Eigen Value and Eigen Vector (original) (raw)
Eigenvalue and Eigenvector
A matrix usually consists of many scalar elements. Can we characterize a matrix by a few numbers? In particular, our question is given a square matrix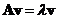
, can we find a scalar number 
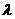and a vector 
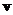such that
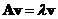? Any solution of equation 
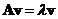for 
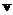is called eigenvector of
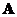. The scalar is called the eigenvalue of matrix
.
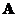Eigenvalue is also called proper value, characteristic value, latent value, or latent root. Similarly, eigenvector is also called proper vector, characteristic vector, or latent vector.
In the topic of Linear Transformation, we learned that a multiplication of a matrix with a vector will produce the transformation of the vector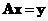
. Notice the equation 
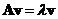said that multiplication of a matrix by a vector is equal to multiplication of a scalar by the same vector. Thus, the scalar 
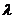characterizes the matrix
.
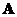Since eigenvalue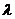 
is the scalar multiple to eigenvector
, geometrically, eigenvalue indicates how much the eigenvector
is shortened or lengthened after multiplication by the matrix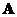
without changing the vector orientation.
Algebraically, we can solve the equation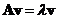 
by rearranging it into a homogeneous linear system 
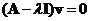where matrix 
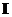is the identity matrix order
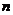. A homogeneous linear system has non trivia solution if the matrix 
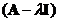is singular. That happens when the determinant is equal to zero, that is
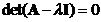. Equation is called the characteristic equation of matrix
.
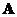Expanding the determinant formula (using cofactor), we will get the solution in the polynomial form with coefficients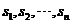
. This polynomial equation 
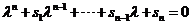is called the characteristic polynomial of matrix
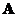. The solution of the characteristic polynomial of 
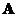are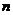 
eigenvalues, some eigenvalues may be identical (the same eigenvalues) and some eigenvalues may be complex numbers.
Each eigenvalue has a corresponding eigenvector. To find the eigenvector, we put back the eigenvalue into equation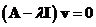
. We do that for each of the eigenvalue. If 
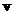is an eigenvector of A, then any scalar multiple is also an eigenvector with the same eigenvalue. We often use normalized eigenvector into unit vector such that the inner product with itself is one
.
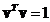Example:
Find eigenvalues and eigenvectors of matrix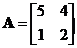
Solution: we form characteristic equation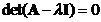
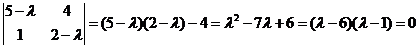
The eigenvalues are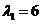
and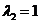
.
For the first eigenvalue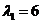
, the system equation is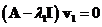
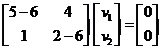
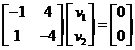
The two rows are equivalent and produces equation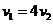
. This is an equation of a line with many solutions, we can put arbitrary value 
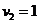to obtain
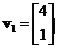. You can also write as 
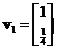or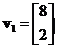 
and they lie on the same line.
The normalized eigenvector is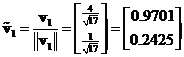 
For the second eigenvalue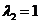
, the eigenvector is computed from the system equation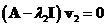 
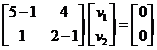
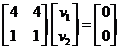
The two rows are equivalent and produces equation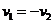
. This is an equation of a line with many solutions, arbitrarily we can put 
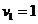to obtain
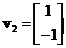. You can also write as 
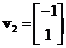or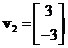 
and they lie on the same line.
The normalized eigenvector is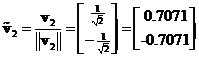
Thus, eigenvalue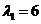 
has corresponding eigenvector
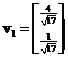and eigenvalue 
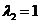has corresponding eigenvector
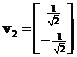. Note that the eigenvectors are actually lines with many solutions and we put only one of the solutions. They are correct up to a scalar multiple. Since the eigenvalues are all distinct, the matrix is diagonalizable and the eigenvectors are linearly independent.
Properties
Some important properties of eigenvalue, eigenvectors and characteristic equation are:
Interactive Eigenvalue and eigen vectors below are useful to compute general square matrix. You can select from the matrix example and click 'Compute Eigenvalues and Eigenvectors' button. This is a working progress, thus the result are not perfect yet, sometimes it would still produce inaccurate results.
See also: Matrix Eigen Value & Eigen Vector for Symmetric Matrix, Similarity and Matrix Diagonalization, Matrix Power
Rate this tutorial or give your comments about this tutorial
Preferable reference for this tutorial is
Teknomo, Kardi (2011) Linear Algebra tutorial. https:\\people.revoledu.com\kardi\tutorial\LinearAlgebra\