Elliptic curves and the ECPP test (original) (raw)

Finding primes & proving primality 4.2: Using elliptic curves and the ECPP test

Elliptic Curves

What is the next big leap in primality proving? To switch from Galois groups to some other, perhaps easier to work with groups--in this case the points on Elliptic Curves modulo n. An Elliptic curve is a curve of genus one, that is a curve that can be written in the form

E(a,b) : _y_2 = _x_3 + ax + b (with 4_a_3 + 27_b_2 not zero)

They are called "elliptic" because these equations first arose in the calculation of the arc-lengths of ellipses.

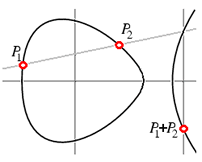The rational points on such a curve form a group with addition defined using the "chord and tangent method:" That is, if the two points P1 and P2 are rational (have rational coefficients), then the line through P1 and P2 intersects the curve again in a third rational point which we call -(P1+P2) (the negative is to make the associative law work out). Reflect through the _x_-axis to get P1+P2. (If P1 and P2 are not distinct, then use the tangent line at P1.)

If we then reduce this group modulo a prime p we get a small group E(a,b)/p whose size can be used in roughly the way we use the size of (Z/pZ)* in the first of the classical tests. Let |E| be the order (the size) of the group E:

Theorem: |E(a,b)/p| lies in the interval (p+1-2sqrt(p),p+1+2sqrt(p)) and the orders are fairly uniformly distributed (as we vary a and b).

Obviously we are again getting out of our depth, but perhaps you see that we now have replaced the groups of order _n_-1 and n+1 used in the classical test with a far larger range of group sizes. We can keep switching curves until we find one we can "factor." This improvement comes at the cost of having to do a great deal of work to find the actual size of these groups.

About 1986, S. Goldwasser & J. Kilian [GK86] and A. O. L. Atkin [Atkin86] introduced elliptic curve primality proving methods. Atkin's method, ECPP, was implemented by a number of mathematicians, including Atkin & Morain [AM93]. François Morain's C-code (discussed in [AM93]) is available on the web for many platforms. For Windows based platforms the Primo implementation is easier to use.

Heuristically, the best version of ECPP is O((log n)4+eps) for some eps > 0 [LL90] (see also D. J. Bernstein's page http://cr.yp.to/primetests.html). It has been proven to be polynomial time for almost all choices of inputs.