Binomial: Symmetric coefficients—Wolfram Documentation (original) (raw)
BUILT-IN SYMBOL
Binomial
Binomial[n,m]
gives the binomial coefficient ![TemplateBox[{n, m}, Binomial]](http://reference.wolfram.com/language/ref/Files/Binomial.en/1.png) .
.
Details

Background & Context
- Binomial represents the binomial coefficient function, which returns the binomial coefficient
![TemplateBox[{n, k}, Binomial]](http://reference.wolfram.com/language/ref/Files/Binomial.en/15.png) of
of 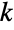 and
and 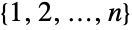 . For non-negative integers
. For non-negative integers 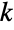 and
and 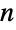 , the binomial coefficient has value
, the binomial coefficient has value ![TemplateBox[{n, k}, Binomial]=(n!)/(k! (n-k)!)](http://reference.wolfram.com/language/ref/Files/Binomial.en/20.png) , where
, where 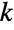 is the Factorial function. By symmetry,
is the Factorial function. By symmetry, ![TemplateBox[{n, k}, Binomial]=TemplateBox[{n, {n, -, k}}, Binomial]](http://reference.wolfram.com/language/ref/Files/Binomial.en/22.png) . The binomial coefficient is important in probability theory and combinatorics and is sometimes also denoted
. The binomial coefficient is important in probability theory and combinatorics and is sometimes also denoted 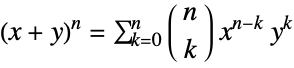
- For non-negative integers
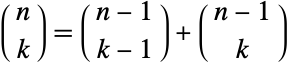 and
and 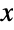 , the binomial coefficient
, the binomial coefficient ![TemplateBox[{n, k}, Binomial]](http://reference.wolfram.com/language/ref/Files/Binomial.en/26.png) gives the number of subsets of length
gives the number of subsets of length 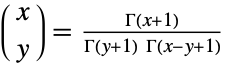 contained in the set
contained in the set 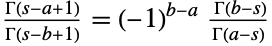 . This is also the number of distinct ways of picking
. This is also the number of distinct ways of picking 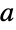 elements (without replacement and ignoring order) from the first
elements (without replacement and ignoring order) from the first 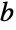 positive integers and for this reason is often voiced as "
positive integers and for this reason is often voiced as "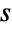 choose
choose 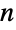 ".
". - The binomial coefficient lies at the heart of the binomial formula, which states that for any non-negative integer
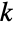 ,
, ![(x+y)^n=sum_(k=0)^nTemplateBox[{n, k}, Binomial] x^(n-k)y^k](http://reference.wolfram.com/language/ref/Files/Binomial.en/34.png) . This interpretation of binomial coefficients is related to the binomial distribution of probability theory, implemented via BinomialDistribution. Another important application is in the combinatorial identity known as Pascal's rule, which relates the binomial coefficient with shifted arguments according to
. This interpretation of binomial coefficients is related to the binomial distribution of probability theory, implemented via BinomialDistribution. Another important application is in the combinatorial identity known as Pascal's rule, which relates the binomial coefficient with shifted arguments according to ![TemplateBox[{n, k}, Binomial]=TemplateBox[{{n, -, 1}, {k, -, 1}}, Binomial]+TemplateBox[{{n, -, 1}, k}, Binomial]](http://reference.wolfram.com/language/ref/Files/Binomial.en/35.png) .
. - Expressing factorials as gamma functions generalizes the binomial coefficient to complex
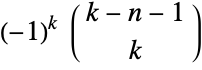 and
and 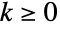 as
as ![TemplateBox[{x, y}, Binomial]=(TemplateBox[{{x, +, 1}}, Gamma])/(TemplateBox[{{y, +, 1}}, Gamma] TemplateBox[{{x, -, y, +, 1}}, Gamma])](http://reference.wolfram.com/language/ref/Files/Binomial.en/38.png) . Using the symmetry formula
. Using the symmetry formula ![(TemplateBox[{{s, -, a, +, 1}}, Gamma])/(TemplateBox[{{s, -, b, +, 1}}, Gamma])=(-1)^(b-a)( TemplateBox[{{b, -, s}}, Gamma])/(TemplateBox[{{a, -, s}}, Gamma])](http://reference.wolfram.com/language/ref/Files/Binomial.en/39.png) for integer
for integer 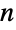 and
and 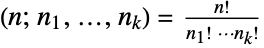 and complex
and complex 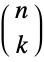 then allows the definition of the binomial coefficient to be extended to negative integer arguments, making it continuous at all integer arguments as well as continuous for all complex arguments except for negative integer
then allows the definition of the binomial coefficient to be extended to negative integer arguments, making it continuous at all integer arguments as well as continuous for all complex arguments except for negative integer 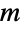 and noninteger
and noninteger 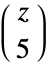 (in which case it is infinite). This definition for negative
(in which case it is infinite). This definition for negative 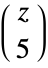 and integer
and integer 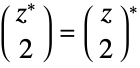 , given by
, given by ![(-1)^k TemplateBox[{{k, -, n, -, 1}, k}, Binomial]](http://reference.wolfram.com/language/ref/Files/Binomial.en/47.png) if
if 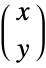 ,
, ![(-1)^(n-k) TemplateBox[{{{-, k}, -, 1}, {n, -, k}}, Binomial]](http://reference.wolfram.com/language/ref/Files/Binomial.en/49.png) if
if 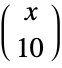 and 0 otherwise, is in agreement with both the binomial theorem and most combinatorial identities (with a few special exceptions).
and 0 otherwise, is in agreement with both the binomial theorem and most combinatorial identities (with a few special exceptions). - Binomial coefficients are generalized by multinomial coefficients. Multinomial returns the multinomial coefficient (n;n1,…,nk) of given numbers n1,…,nk summing to
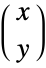 , where
, where 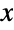 . The binomial coefficient
. The binomial coefficient ![TemplateBox[{n, k}, Binomial]](http://reference.wolfram.com/language/ref/Files/Binomial.en/53.png) is the multinomial coefficient (n;k,n-k).
is the multinomial coefficient (n;k,n-k).
Examples
open allclose all
Basic Examples (5)
Evaluate numerically:
Evaluate symbolically:
Construct Pascal's triangle:
Plot over a subset of the reals as a function of its first parameter:
Plot over a subset of the reals as a function of its second parameter:
Plot over a subset of the complexes:
Scope (35)
Numerical Evaluation (7)
Evaluate numerically:
Evaluate for half-integer arguments:
Evaluate to high precision:
The precision of the output tracks the precision of the input:
Complex number inputs:
Evaluate efficiently at high precision:
Compute worst-case guaranteed intervals using Interval and CenteredInterval objects:
Or compute average-case statistical intervals using Around:
Compute the elementwise values of an array:
Or compute the matrix Binomial function using MatrixFunction:
Specific Values (4)
Values of Binomial at particular points:
Binomial for symbolic n:
Values at zero:
Note that this is zero on all integers away from 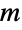 :
:
Find a value of n for which Binomial[n,2]=15:
Visualization (3)
Plot the Binomial as a function of its parameter n:
Plot the Binomial as a function of its parameter 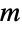 :
:
Plot the real part of ![TemplateBox[{z, 5}, Binomial]](http://reference.wolfram.com/language/ref/Files/Binomial.en/56.png) :
:
Plot the imaginary part of ![TemplateBox[{z, 5}, Binomial]](http://reference.wolfram.com/language/ref/Files/Binomial.en/57.png) :
:
Function Properties (12)
Real domain of Binomial as a function of its parameter n:
Real domain of Binomial as a function of its parameter m:
Complex domains:
Function range of Binomial:
Binomial has the mirror property ![TemplateBox[{TemplateBox[{z}, Conjugate, SyntaxForm -> SuperscriptBox], 2}, Binomial]=TemplateBox[{TemplateBox[{z, 2}, Binomial]}, Conjugate]](http://reference.wolfram.com/language/ref/Files/Binomial.en/58.png "TemplateBox[{TemplateBox[{z}, Conjugate, SyntaxForm -> SuperscriptBox], 2}, Binomial]=TemplateBox[{TemplateBox[{z, 2}, Binomial]}, Conjugate]"):
Compute sums involving Binomial:
When 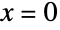 is positive,
is positive, ![TemplateBox[{x, y}, Binomial]](http://reference.wolfram.com/language/ref/Files/Binomial.en/60.png) is an analytic function of both variables:
is an analytic function of both variables:
This is not true for negative 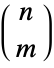 :
:
![TemplateBox[{x, 7}, Binomial]](http://reference.wolfram.com/language/ref/Files/Binomial.en/62.png) is neither non-decreasing nor non-increasing:
is neither non-decreasing nor non-increasing:
![TemplateBox[{x, 7}, Binomial]](http://reference.wolfram.com/language/ref/Files/Binomial.en/63.png) is not injective:
is not injective:
![TemplateBox[{x, 7}, Binomial]](http://reference.wolfram.com/language/ref/Files/Binomial.en/64.png) is surjective:
is surjective:
Binomial is neither non-negative nor non-positive:
![TemplateBox[{x, y}, Binomial]](http://reference.wolfram.com/language/ref/Files/Binomial.en/65.png) has singularities and discontinuities where
has singularities and discontinuities where 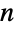 is a negative integer:
is a negative integer:
![TemplateBox[{x, 7}, Binomial]](http://reference.wolfram.com/language/ref/Files/Binomial.en/67.png) is neither convex nor concave:
is neither convex nor concave:
TraditionalForm formatting:
Differentiation (3)
First derivative with respect to 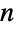 :
:
Higher derivatives with respect to 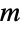 :
:
Plot the higher derivatives with respect to 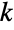 for
for 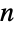 :
:
First derivative with respect to  :
:
Series Expansions (4)
Find the Taylor expansion using Series:
Plots of the first three approximations around 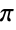 :
:
Find the series expansion at Infinity:
Find series expansion for an arbitrary symbolic direction  :
:
Taylor expansion at a generic point:
Function Identities and Simplifications (2)
Functional identity:
Recurrence relations:
Generalizations & Extensions (2)
Infinite arguments give symbolic results:
Binomial threads elementwise over lists:
Applications (11)
There are ![TemplateBox[{n, m}, Binomial]](http://reference.wolfram.com/language/ref/Files/Binomial.en/75.png) ways to choose
ways to choose  elements without replacements from a set of
elements without replacements from a set of  elements:
elements:
Check with direct enumeration:
There are ![TemplateBox[{{m, +, n, -, 1}, m}, Binomial]](http://reference.wolfram.com/language/ref/Files/Binomial.en/78.png) ways to choose
ways to choose  elements with replacement from a set of
elements with replacement from a set of  elements:
elements:
Check with direct enumeration:
There are ![TemplateBox[{{m, +, n}, m}, Binomial]](http://reference.wolfram.com/language/ref/Files/Binomial.en/81.png) ways to arrange
ways to arrange  indistinguishable objects of one kind, and
indistinguishable objects of one kind, and  indistinguishable objects of another kind:
indistinguishable objects of another kind:
Illustrate the binomial theorem:
Fractional binomial theorem:
Binomial coefficients mod 2:
Plot Binomial in the arguments' plane:
Plot the logarithm of the number of ways to pick  elements out of
elements out of  :
:
Compute higher derivatives of a product of two functions:
PDF of the binomial probability distribution:
Bernstein polynomials are defined in terms of Binomial:
Properties & Relations (11)
On the integers, Binomial[n,m] equals ![TemplateBox[{{{(, TemplateBox[{{n, +, epsilon, +, 1}}, Gamma], )}, /, {(, {TemplateBox[{{m, +, epsilon, +, 1}}, Gamma], , TemplateBox[{{{-, m}, +, n, +, epsilon, +, 1}}, Gamma]}, )}}, epsilon, 0, TemplateBox[{}, Complexes]}, LimitWithTooltip]](http://reference.wolfram.com/language/ref/Files/Binomial.en/86.png "TemplateBox[{{{(, TemplateBox[{{n, +, epsilon, +, 1}}, Gamma], )}, /, {(, {TemplateBox[{{m, +, epsilon, +, 1}}, Gamma], , TemplateBox[{{{-, m}, +, n, +, epsilon, +, 1}}, Gamma]}, )}}, epsilon, 0, TemplateBox[{}, Complexes]}, LimitWithTooltip]"):
This can be expressed as ![(-1)^m TemplateBox[{{-, n}, m}, Pochhammer]/m!](http://reference.wolfram.com/language/ref/Files/Binomial.en/87.png) for
for  and
and ![(-1)^(n-m) TemplateBox[{{-, n}, {n, -, m}}, Pochhammer]/(n-m)!](http://reference.wolfram.com/language/ref/Files/Binomial.en/89.png) for
for  :
:
An alternative formula on the integers:
Pascal's identity is satisfied almost everywhere:
It is violated at the origin:
PascalBinomial satisfies the identity everywhere, including the origin:
The symmetry rule ![TemplateBox[{n, m}, PascalBinomial]=TemplateBox[{n, {n, -, m}}, PascalBinomial]](http://reference.wolfram.com/language/ref/Files/Binomial.en/91.png) holds for all values of
holds for all values of  and
and  :
:
PascalBinomial performs simple evaluations for symbolic arguments:
For more complex expressions, it will avoid automatic expansion:
Use FunctionExpand with conditions to achieve appropriate simplifications:
Use FullSimplify to simplify expressions involving binomial coefficients:
Use FunctionExpand to expand into Gamma functions:
Sums involving Binomial:
Find the generating function Binomial:
Binomial can be represented as a DifferenceRoot:
The generating function for Binomial:
The exponential generating function for Binomial:
Possible Issues (3)
Large arguments can give results too large to be computed explicitly:

Machine-number inputs can give high‐precision results:
As a bivariate function, Binomial is not continuous in both variables at negative integers:
The value of Binomial at negative integers is determined via Binomial[n,m]Binomial[n,n-m]:
Neat Examples (7)
Construct a graphical version of Pascal's triangle:
Extend the triangle to negative integers; unlabeled points indicate a zero value:
PascalBinomial, by contrast, zeroes out the top-left sector where both inputs are negative:
Binomial coefficient mod  :
:
Closed‐form inverse of Hilbert matrices:
Nested binomials over the complex plane:
Plot Binomial at infinity:
Plot Binomial for complex arguments:
Plot Binomial at Gaussian integers:
Related Guides
▪
- Combinatorial Functions ▪
- Discrete Mathematics ▪
- Functions Used in Statistics ▪
- Mathematical Functions ▪
- Integer Functions ▪
- Integer Sequences ▪
- Recurrence and Sum Functions ▪
- Gamma Functions and Related Functions
History
Introduced in 1988 (1.0)
Wolfram Research (1988), Binomial, Wolfram Language function, https://reference.wolfram.com/language/ref/Binomial.html.
Text
Wolfram Research (1988), Binomial, Wolfram Language function, https://reference.wolfram.com/language/ref/Binomial.html.
CMS
Wolfram Language. 1988. "Binomial." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/Binomial.html.
APA
Wolfram Language. (1988). Binomial. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/Binomial.html
BibTeX
@misc{reference.wolfram_2025_binomial, author="Wolfram Research", title="{Binomial}", year="1988", howpublished="\url{https://reference.wolfram.com/language/ref/Binomial.html}", note=[Accessed: 18-June-2025 ]}
BibLaTeX
@online{reference.wolfram_2025_binomial, organization={Wolfram Research}, title={Binomial}, year={1988}, url={https://reference.wolfram.com/language/ref/Binomial.html}, note=[Accessed: 18-June-2025 ]}