BipartiteGraphQ—Wolfram Language Documentation (original) (raw)
BUILT-IN SYMBOL
BipartiteGraphQ
Background & Context
- BipartiteGraphQ tests if a specified graph is bipartite. A graph is bipartite if its vertex set can be partitioned into two independent sets (called the "partite sets")
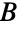and 
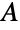, where an independent set of vertices satisfies the condition that no two of its vertices are part of the same edge. In other words, all edges of a bipartite graph have one endpoint in 
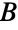and one in 
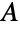. BipartiteGraphQ returns True if a graph is bipartite and False otherwise. Equivalent conditions for a graph being bipartite include lacking cycles of odd length and having a chromatic number at most two. Trees (and forests) contain no cycles and hence are automatically bipartite. Families of bipartite graphs include cycle graphs with even vertex count, grid graphs, hypercube graphs, knight graphs, and star graphs (which are bipartite by virtue of being trees). - Bipartite graphs arise naturally in the modeling of certain assignment problems. For example, given a set
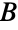of workers and set 
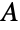of full-time jobs, construct a bipartite graph having partite sets 
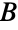and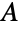 
with edges joining a worker and a job if that worker is qualified to perform that job. Finding an assignment of workers to jobs that maximizes employment is equivalent to finding a maximum independent edge set. - Many fundamental results in graph theory involve bipartite graphs. König's line coloring theorem states that bipartite graphs have edge chromatic number equal to their maximum degree. The König–Egerváry theorem states that for bipartite graphs, the maximum size of an independent edge set equals the minimum size of a vertex cover. Ore's defect formula states that if a graph has partite sets
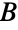and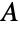 
, then this common value equals the size of 
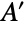minus the maximum, over all subsets 
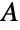of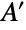 
, of the size of 
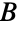minus the number of vertices in 
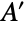adjacent to some vertex in 
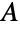. In the special case that no subset of 
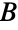has more vertices than it has neighbors in 
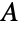, Ore's defect formula becomes Hall's marriage theorem, which states that this condition is equivalent to the existence of an independent set of edges incident to every vertex of 
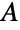. - CompleteGraph[{m,n}] returns a complete bipartite graph on partite sets
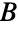and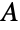 
of sizes m and n, respectively, which is a bipartite graph in which every vertex in 
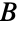is connected to every vertex in 
.
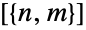Examples
open allclose all
Basic Examples (2)
Test whether a graph is bipartite:
Not all graphs are bipartite:
Scope (6)
Properties & Relations (8)
A bipartite graph has no self-loops:
Any tree is bipartite:
A PathGraph with different start and end vertices is bipartite:
Any planar graph whose faces all consist of an even number of edges is bipartite:
A CycleGraph with an even number of vertices is bipartite:
A CompleteGraph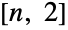 
is bipartite:
A TuranGraph 
is bipartite:
A graph is bipartite iff it has no odd cycle:
Wolfram Research (2010), BipartiteGraphQ, Wolfram Language function, https://reference.wolfram.com/language/ref/BipartiteGraphQ.html.
Text
Wolfram Research (2010), BipartiteGraphQ, Wolfram Language function, https://reference.wolfram.com/language/ref/BipartiteGraphQ.html.
CMS
Wolfram Language. 2010. "BipartiteGraphQ." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/BipartiteGraphQ.html.
APA
Wolfram Language. (2010). BipartiteGraphQ. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/BipartiteGraphQ.html
BibTeX
@misc{reference.wolfram_2025_bipartitegraphq, author="Wolfram Research", title="{BipartiteGraphQ}", year="2010", howpublished="\url{https://reference.wolfram.com/language/ref/BipartiteGraphQ.html}", note=[Accessed: 01-May-2025 ]}
BibLaTeX
@online{reference.wolfram_2025_bipartitegraphq, organization={Wolfram Research}, title={BipartiteGraphQ}, year={2010}, url={https://reference.wolfram.com/language/ref/BipartiteGraphQ.html}, note=[Accessed: 01-May-2025 ]}