Complex—Wolfram Language Documentation (original) (raw)

BUILT-IN SYMBOL

Complex

is the head used for complex numbers.

Details

You can enter a complex number in the form x+Iy.
_Complex can be used to stand for a complex number in a pattern.
You have to use Re and Im to extract parts of Complex numbers.

Examples

open allclose all

Basic Examples (1)

Enter a complex number:

Complex is the Head for complex numbers:

Scope (9)

Enter a purely imaginary number:

Even though there is no real part it has Head Complex:

The FullForm of a complex number x+Iy is Complex[x,y]:

Enter a complex number using the FullForm:

If the imaginary part is exactly zero, then the result is not Complex:

You have to use Re and Im to extract parts of Complex numbers:

Part does not work:

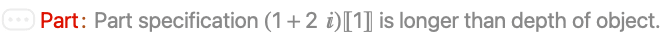
If either part of a complex number has machine precision, the entire number has machine precision:

Verify that the result is indeed a machine number:

Enter a complex number with an exact real part and an arbitrary-precision imaginary part:

The exactness is kept in computations when possible:

This is not, in general, possible:

Enter a complex number with arbitrary-precision real and imaginary parts:

The precision is based on the error in the complex plane:

_Complex can be used to stand for a complex number in a pattern:

A rule that switches real and imaginary parts:

An alternate definition:

Applications (2)

Define a function over the complexes by using functions defined over the reals:

Multiply all pure imaginary numbers in an expression by a constant:

Note that the naive replacement Ia I would only multiply occurrences of I===Complex[0,1]:

Properties & Relations (5)

Complexes are numbers:

Complexes are atomic objects with no subexpressions:

Use Complexes to indicate assumptions on domain conditions:

Real and imaginary parts of complex numbers can have different precisions:

Arithmetic operations will typically mix them:

But note that real and imaginary parts still have different precisions:

The precision of the whole number lies in between these two precisions:

Machine-precision evaluation of pure imaginary numbers yields an approximate zero real part:

Arbitrary‐precision evaluation yields an exact zero real part:

Possible Issues (2)

Numbers entered in the form x+Iy only become Complex numbers on evaluation:

The unevaluated form is expressed in terms of Plus and Times:

Evaluated complex numbers are atomic objects and do not explicitly contain I:

Patterns of the form Complex[x_,y_] can be used to match the whole complex number:

History

Introduced in 1988 (1.0)

Wolfram Research (1988), Complex, Wolfram Language function, https://reference.wolfram.com/language/ref/Complex.html.

Text

Wolfram Research (1988), Complex, Wolfram Language function, https://reference.wolfram.com/language/ref/Complex.html.

CMS

Wolfram Language. 1988. "Complex." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/Complex.html.

APA

Wolfram Language. (1988). Complex. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/Complex.html

BibTeX

@misc{reference.wolfram_2025_complex, author="Wolfram Research", title="{Complex}", year="1988", howpublished="\url{https://reference.wolfram.com/language/ref/Complex.html}", note=[Accessed: 17-June-2025 ]}

BibLaTeX

@online{reference.wolfram_2025_complex, organization={Wolfram Research}, title={Complex}, year={1988}, url={https://reference.wolfram.com/language/ref/Complex.html}, note=[Accessed: 17-June-2025 ]}