Complexes—Wolfram Language Documentation (original) (raw)

BUILT-IN SYMBOL

Complexes

represents the domain of complex numbers, as in x∈Complexes.

open allclose all

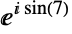is a complex number:

Exponential of a complex number is a complex number:

Find complex numbers that make an inequality well defined and True:

Specify that all variables should be considered complex, even if they appear in inequalities:

By default, Reduce considers all variables that appear in inequalities to be real:

For every real number y there exists a complex number whose square is real and less than y:

By default, Resolve considers all variables that appear in inequalities to be real:

Wolfram Research (1999), Complexes, Wolfram Language function, https://reference.wolfram.com/language/ref/Complexes.html (updated 2017).

Wolfram Research (1999), Complexes, Wolfram Language function, https://reference.wolfram.com/language/ref/Complexes.html (updated 2017).

Wolfram Language. 1999. "Complexes." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2017. https://reference.wolfram.com/language/ref/Complexes.html.

Wolfram Language. (1999). Complexes. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/Complexes.html

@misc{reference.wolfram_2025_complexes, author="Wolfram Research", title="{Complexes}", year="2017", howpublished="\url{https://reference.wolfram.com/language/ref/Complexes.html}", note=[Accessed: 16-June-2025 ]}

@online{reference.wolfram_2025_complexes, organization={Wolfram Research}, title={Complexes}, year={2017}, url={https://reference.wolfram.com/language/ref/Complexes.html}, note=[Accessed: 16-June-2025 ]}