Convolve—Wolfram Language Documentation (original) (raw)

BUILT-IN SYMBOL

• See Also
  • Integrate
  • UnilateralConvolve
  • DiscreteConvolve
  • MellinConvolve
  • LaplaceTransform
  • FourierTransform
  • DiracDelta
  • HeavisideTheta
  • HeavisidePi
  • HeavisideLambda
  • GreenFunction
• Related Guides
  • Integral Transforms
  • Fourier Analysis
  • Generalized Functions
  • Calculus

Convolve

Convolve[f,g,x,y]

gives the convolution with respect to x of the expressions f and g.

Convolve[f,g,{x1,x2,…},{y1,y2,…}]

gives the multidimensional convolution.

Details and Options

Examples

open allclose all

Basic Examples (3)

Convolve a function with DiracDelta:

Convolve two unit pulses:

Convolve two exponential functions and plot the result:

Scope (5)

Univariate Convolution (3)

The convolution gives the product integral of translates:

Elementary functions:

A convolution typically smooths the function:

For this family, they all have unit area:

Multivariate Convolution (2)

The convolution gives the product integral of translates:

Convolution with multivariate delta functions acts as a point operator:

Convolution with a function of bounded support acts as a filter:

Generalizations & Extensions (1)

Multiplication by UnitStep effectively gives the convolution on a finite interval:

Options (2)

Assumptions (1)

Specify assumptions on a variable or parameter:

GenerateConditions (1)

Generate conditions for the range of a parameter:

Applications (5)

Properties & Relations (7)

Convolve computes an integral over the real line:

Convolution with DiracDelta gives the function itself:

Scaling:

Commutativity:

Distributivity:

The Laplace transform of a causal convolution is a product of the individual transforms:

The Fourier transform of a convolution is related to the product of the individual transforms:

Interactive Examples (1)

This demonstrates the convolution operation :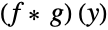

Wolfram Research (2008), Convolve, Wolfram Language function, https://reference.wolfram.com/language/ref/Convolve.html.

Text

Wolfram Research (2008), Convolve, Wolfram Language function, https://reference.wolfram.com/language/ref/Convolve.html.

CMS

Wolfram Language. 2008. "Convolve." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/Convolve.html.

APA

Wolfram Language. (2008). Convolve. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/Convolve.html

BibTeX

@misc{reference.wolfram_2025_convolve, author="Wolfram Research", title="{Convolve}", year="2008", howpublished="\url{https://reference.wolfram.com/language/ref/Convolve.html}", note=[Accessed: 16-June-2025 ]}

BibLaTeX

@online{reference.wolfram_2025_convolve, organization={Wolfram Research}, title={Convolve}, year={2008}, url={https://reference.wolfram.com/language/ref/Convolve.html}, note=[Accessed: 16-June-2025 ]}