DivisorSum—Wolfram Language Documentation (original) (raw)

BUILT-IN SYMBOL

• See Also
  • DivisorSigma
  • Divisors
  • DigitSum
  • DirichletConvolve
  • DirichletTransform
  • MoebiusMu
  • Sum
  • RootSum
• Related Guides
  • Number Theoretic Functions
  • Multiplicative Number Theory
  • Number Theory
  • Analytic Number Theory
  • Additive Number Theory

DivisorSum

DivisorSum[n,form]

represents the sum of form[i] for all i that divide n.

DivisorSum[n,form,cond]

includes only those divisors for which cond[i] gives True.

Details

• Integer mathematical function, suitable for both symbolic and numerical manipulation.
• n can be symbolic or a positive integer.
• form and cond must be Function objects.
• DivisorSum[n,form] is equivalent to Sum[form[d],{d,Divisors[n]}] for positive n.
• DivisorSum[n,form,cond] is automatically simplified when n is a positive integer.
• DivisorSum[n,form] is automatically simplified when form is a polynomial function.

Examples

open allclose all

Basic Examples (2)

Find the sum of the divisors of :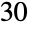

Plot the sum of divisors for the first 50 numbers:

Scope (12)

Numerical Evaluation (5)

DivisorSum works over formal expressions:

Exact values are generated at positive integers:

Conditions on divisors can be specified:

Compute for large numbers:

DivisorSum threads elementwise over lists:

Symbolic Manipulation (7)

TraditionalForm formatting:

DivisorSum automatically simplifies for polynomial functions:

Reduce expressions:

Solve equations:

Simplify expressions:

Compute sums symbolically:

Generating function:

Applications (8)

Basic Applications (3)

Plot the sum of divisors for the first 100 numbers:

Classical identities:

Sum of powers:

Number Theory (5)

Compute the Lambert series for Euler's totient function:

Compute Jordan's totient function: [more info]

When 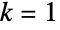, this is equivalent to Euler's totient function:

Compute the twisted divisor sum:

Define the unitary convolution:

Compute the number of polynomials over 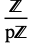that are irreducible of degree n:

Irreducible polynomials modulo 5:

Distribution of irreducible polynomials modulo 5:

Logarithmic plot of the count for :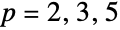

Properties & Relations (4)

Use Divisors to compute DivisorSum:

DivisorSigma gives the sum of powers of divisors of an integer:

DivisorSum[n,form] is equivalent to Sum[form[d],{d,Divisors[n]}] for positive n:

The sum of the prime divisors of a prime number returns the original number:

Possible Issues (2)

The arguments to DivisorSum are not affected by N:

After evaluation, results may be affected by N:

Only divisors that explicitly yield True on the conditions are used:

Wolfram Research (2008), DivisorSum, Wolfram Language function, https://reference.wolfram.com/language/ref/DivisorSum.html.

Text

Wolfram Research (2008), DivisorSum, Wolfram Language function, https://reference.wolfram.com/language/ref/DivisorSum.html.

CMS

Wolfram Language. 2008. "DivisorSum." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/DivisorSum.html.

APA

Wolfram Language. (2008). DivisorSum. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/DivisorSum.html

BibTeX

@misc{reference.wolfram_2025_divisorsum, author="Wolfram Research", title="{DivisorSum}", year="2008", howpublished="\url{https://reference.wolfram.com/language/ref/DivisorSum.html}", note=[Accessed: 30-April-2025 ]}

BibLaTeX

@online{reference.wolfram_2025_divisorsum, organization={Wolfram Research}, title={DivisorSum}, year={2008}, url={https://reference.wolfram.com/language/ref/DivisorSum.html}, note=[Accessed: 30-April-2025 ]}