EllipticPi—Wolfram Language Documentation (original) (raw)

BUILT-IN SYMBOL

• See Also
  • EllipticK
  • EllipticF
  • EllipticE
  • CarlsonRM
  • CarlsonRJ
  • CarlsonRC
• Related Guides
  • Elliptic Integrals
  • Special Functions
• Tech Notes
  • Elliptic Integrals and Elliptic Functions

EllipticPi

EllipticPi[n,m]

gives the complete elliptic integral of the third kind .

EllipticPi[n,ϕ,m]

gives the incomplete elliptic integral .

Details

Examples

open allclose all

Basic Examples (6)

Evaluate numerically:

Plot over a subset of the reals:

Plot over a subset of the complexes:

Plot the incomplete elliptic integral over a subset of the complexes:

Series expansions at the origin:

Series expansion at Infinity:

Scope (36)

Numerical Evaluation (6)

Evaluate the incomplete elliptic integral numerically:

Evaluate to high precision:

The precision of the output tracks the precision of the input:

Evaluate for complex arguments:

Evaluate EllipticPi efficiently at high precision:

Compute worst-case guaranteed intervals using Interval and CenteredInterval objects:

Or compute average-case statistical intervals using Around:

Compute the elementwise values of an array:

Or compute the matrix EllipticPi function using MatrixFunction:

Specific Values (3)

Simple exact values are generated automatically:

Values at infinity:

Find a real root of the equation :

Visualization (4)

Plot EllipticPi for various values of the second parameter :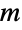

Plot EllipticPi for various values of the first parameter :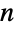

Plot the incomplete elliptic integral for various values of parameter :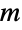

Plot the real part of :

Plot the imaginary part of :

Function Properties (9)

EllipticPi is not an analytic function:

Has both singularities and discontinuities:

EllipticPi is not a meromorphic function:

Real domain of :

Real range of :

Convert to a numerical approximation:

is neither nondecreasing nor nonincreasing:

is injective:

is not surjective:

is neither non-negative nor non-positive:

is neither convex nor concave:

Differentiation (4)

First derivative with respect to the first parameter:

Higher derivatives:

Plot higher derivatives for :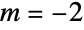

Differentiate with the respect to the second argument:

Higher derivatives:

Plot higher derivatives for :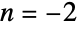

Integration (3)

Indefinite integral with respect to :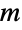

Definite integral:

Integral involving the incomplete elliptic integral:

Series Expansions (3)

Taylor expansion for EllipticPi around :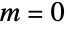

Plot the first three approximations for around :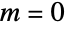

Series expansion for EllipticPi around the branch point :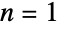

Plot the first three approximations for around :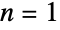

EllipticPi can be applied to power series:

Function Representations (4)

Integral representation:

The complete elliptic integral of the third kind is a partial case of the incomplete elliptic integral:

EllipticPi can be represented as a DifferentialRoot:

TraditionalForm formatting:

Applications (6)

Evaluate an elliptic integral:

Definition of the solid angle subtended by a disk (for instance a detector, a road sign) at the origin in the 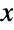, 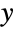‐plane from a point :

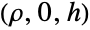Closed form result for the solid angle:

Numerical comparison:

Plot the solid angle as a function of horizontal distance and height:

This calculates the classical action for a relativistic 3D oscillator:

The action can be expressed using EllipticPi (for brevity, occurring roots are abbreviated):

A conformal map:

Visualize the image of lines of constant real and imaginary parts:

Parameterization of genus‐1 constant mean-curvature Wente torus:

Visualize 3‐lobe, 5‐lobe, 7‐lobe and 11‐lobe tori:

Numerically verify various change of parameter relations for EllipticPi:

Properties & Relations (4)

EllipticPi[n,m] is real‐valued for 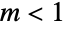and :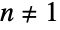

Expand special cases using assumptions:

This shows the branch cuts of the EllipticPi function:

Numerically find a root of a transcendental equation:

Possible Issues (3)

Limits at branch cuts can be wrong:

The defining integral converges only under additional conditions:

Different argument conventions exist that result in modified results:

Wolfram Research (1988), EllipticPi, Wolfram Language function, https://reference.wolfram.com/language/ref/EllipticPi.html (updated 2022).

Text

Wolfram Research (1988), EllipticPi, Wolfram Language function, https://reference.wolfram.com/language/ref/EllipticPi.html (updated 2022).

CMS

Wolfram Language. 1988. "EllipticPi." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2022. https://reference.wolfram.com/language/ref/EllipticPi.html.

APA

Wolfram Language. (1988). EllipticPi. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/EllipticPi.html

BibTeX

@misc{reference.wolfram_2025_ellipticpi, author="Wolfram Research", title="{EllipticPi}", year="2022", howpublished="\url{https://reference.wolfram.com/language/ref/EllipticPi.html}", note=[Accessed: 04-May-2025 ]}

BibLaTeX

@online{reference.wolfram_2025_ellipticpi, organization={Wolfram Research}, title={EllipticPi}, year={2022}, url={https://reference.wolfram.com/language/ref/EllipticPi.html}, note=[Accessed: 04-May-2025 ]}