EulerE—Wolfram Language Documentation (original) (raw)

BUILT-IN SYMBOL

EulerE

gives the Euler number TemplateBox[{n}, EulerE] .

gives the Euler polynomial TemplateBox[{n, x}, EulerE2] .

open allclose all

First 10 EulerE numbers:

Euler polynomials:

EulerE threads elementwise over lists:

Plot Euler polynomials:

Simple exact values are generated automatically:

Implement the Boole summation formula:

First a sequence of approximations to 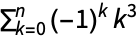sum_(k=0)^n(-1)^kk^3 :

The sequence converges to the exact answer:

Plot roots of Euler polynomials in the complex plane:

Algorithmically produced results are often expressed using Zeta instead of EulerE:

Umbral calculus with Euler numbers:

Histogram of digits of 10000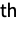 ^(th) Euler number:

The sequence of Euler numbers modulo a fixed number is periodic:

Define a Hankel matrix whose entries are the Euler numbers:

Its determinant can be expressed in terms of the Barnes G-function:

Introduced in 1988 (1.0)

Wolfram Research (1988), EulerE, Wolfram Language function, https://reference.wolfram.com/language/ref/EulerE.html.

Wolfram Research (1988), EulerE, Wolfram Language function, https://reference.wolfram.com/language/ref/EulerE.html.

Wolfram Language. 1988. "EulerE." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/EulerE.html.

Wolfram Language. (1988). EulerE. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/EulerE.html

@misc{reference.wolfram_2025_eulere, author="Wolfram Research", title="{EulerE}", year="1988", howpublished="\url{https://reference.wolfram.com/language/ref/EulerE.html}", note=[Accessed: 30-April-2025 ]}

@online{reference.wolfram_2025_eulere, organization={Wolfram Research}, title={EulerE}, year={1988}, url={https://reference.wolfram.com/language/ref/EulerE.html}, note=[Accessed: 30-April-2025 ]}