Fibonacci—Wolfram Language Documentation (original) (raw)

BUILT-IN SYMBOL

• See Also
  • GoldenRatio
  • LucasL
  • RSolve
  • LinearRecurrence
  • RecurrenceTable
  • DifferenceRoot
  • GoldenAngle
• Related Guides
  • Recurrence and Sum Functions
  • Integer Sequences
  • Discrete Calculus
  • Discrete Mathematics
  • Integer Functions
  • Mathematical Functions
• Tech Notes
  • Combinatorial Functions
  • Implementation notes: Numerical and Related Functions

Fibonacci

Fibonacci[n,x]

gives the Fibonacci polynomial .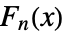

Details

Examples

open allclose all

Basic Examples (6)

Compute Fibonacci numbers:

Plot over a subset of the reals:

Plot over a subset of the complexes:

Series expansion at the origin:

Series expansion at Infinity:

Series expansion at a singular point:

Scope (43)

Numerical Evaluation (6)

Evaluate numerically:

Evaluate to high precision:

The precision of the output tracks the precision of the input:

Complex number inputs:

Evaluate efficiently at high precision:

Compute worst-case guaranteed intervals using Interval and CenteredInterval objects:

Or compute average-case statistical intervals using Around:

Compute the elementwise values of an array:

Or compute the matrix Fibonacci function using MatrixFunction:

Specific Values (6)

Values of Fibonacci at fixed points:

Fibonacci polynomial for symbolic n and x:

Values at zero:

Find the value of 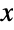in which :

Compute the Fibonacci[7,x] polynomial:

Compute Fibonacci[1/2,x]:

Visualization (5)

Plot the Fibonacci function:

Plot the Fibonacci polynomial for various orders:

Plot the real part of :

Plot the imaginary part of :

Plot as real parts of two parameters vary:

Types 2 and 3 of Fibonacci polynomial have different branch cut structures:

Function Properties (14)

Fibonacci is defined for all real values:

Approximate function range of Fibonacci:

Fibonacci polynomial of an even order is odd:

Fibonacci polynomial of an odd order is even:

Fibonacci has the mirror property :

Fibonacci threads elementwise over lists:

Fibonacci is an analytic function of x:

Fibonacci is neither non-decreasing nor non-increasingfor odd values:

Fibonacci is non-decreasing for even values:

Fibonacci is not injective for odd values:

Fibonacci is not surjective for odd values:

Fibonacci is non-negative for odd values:

Fibonacci has no singularities or discontinuities:

Fibonacci is convex for odd values:

TraditionalForm formatting:

Differentiation (3)

First derivatives with respect to n:

First derivative with respect to x:

Higher derivatives with respect to n:

Plot the higher derivatives with respect to n:

Formula for the 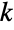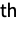derivative with respect to n:

Integration (3)

Compute the indefinite integral using Integrate:

Definite integral:

More integrals:

Series Expansions (4)

Find the Taylor expansion using Series:

Plots of the first three approximations around :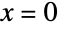

General term in the series expansion using SeriesCoefficient:

Find the series expansion at Infinity:

Taylor expansion at a generic point:

Function Identities and Simplifications (2)

The ordinary generating function of Fibonacci:

Recurrence relation:

Generalizations & Extensions (2)

Fibonacci polynomials:

General series expansion at infinity:

Applications (13)

Solve the Fibonacci recurrence equation:

Solve another Fibonacci recurrence equation:

Find ratios of successive Fibonacci numbers:

Compare with continued fractions:

Convergence to the golden ratio:

Fibonacci substitution system:

Fibonomial coefficients:

Calculate the number of ways to write an integer as a sum of Fibonacci numbers :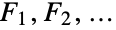

Plot the counts for the first hundred integers:

Lamé's theorem bounds the number of steps of the Euclidean algorithm for calculating :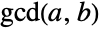

Plot the maximal number of steps:

Find the first Fibonacci number above 1000000:

Plot the discrete inverse of Fibonacci numbers:

Plot of the absolute value of Fibonacci over the complex plane:

Find the number of factors of Fibonacci polynomials:

If 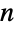divides , then divides ![TemplateBox[{TemplateBox[{m}, Fibonacci]}, Fibonacci]](http://reference.wolfram.com/language/ref/Files/Fibonacci.en/26.png "TemplateBox[{TemplateBox[{m}, Fibonacci]}, Fibonacci]"):

This is a particular case of a more general identity :

The sequence of ![TemplateBox[{TemplateBox[{n}, Fibonacci], m}, Mod]](http://reference.wolfram.com/language/ref/Files/Fibonacci.en/28.png "TemplateBox[{TemplateBox[{n}, Fibonacci], m}, Mod]") is periodic with respect to 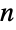for a fixed natural number :

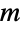For 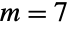, the period equals :

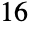Build Zeckendorf's representation of a positive integer [MathWorld]:

Define Fibonacci multiplication for positive integers:

Fibonacci multiplication table:

Verify that the Fibonacci multiplication is associative:

Properties & Relations (15)

Fibonacci Numbers (13)

Expand in terms of elementary functions:

Limiting ratio:

Explicit recursive definition:

Explicit state‐space recursive definition:

Closed‐form solution using MatrixPower:

Simplify expressions involving Fibonacci numbers:

Symbolic summation:

Generating function:

Fibonacci numbers as coefficients:

Express a fractional Fibonacci number as an algebraic number:

Fibonacci can be represented as a DifferenceRoot:

General term in the series expansion of Fibonacci:

The generating function for Fibonacci:

FindSequenceFunction can recognize the Fibonacci sequence:

The exponential generating function for Fibonacci:

Fibonacci Polynomials (2)

Expand in terms of elementary functions:

Explicitly construct Fibonacci polynomials:

Possible Issues (3)

Large arguments can give results too large to be computed explicitly:

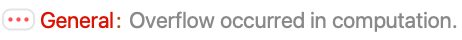
Results for integer arguments may not hold for non-integers:

Matrix power representation is valid only for integers:

Neat Examples (8)

Fibonacci numbers modulo 10:

Fibonacci modulo n [more info]:

Count the number of 1, 2, ..., 9, 0 digits in the 1,000,000 Fibonacci number:

Contours of vanishing real and imaginary parts of Fibonacci:

LogPlot of positive and negative Fibonacci numbers:

While the Fibonacci numbers are nondecreasing for non-negative arguments, the Fibonacci function possesses a single local minimum:

Since the generating function is rational, these sums come out as rational numbers:

Related Guides

▪

• Recurrence and Sum Functions ▪
• Integer Sequences ▪
• Discrete Calculus ▪
• Discrete Mathematics ▪
• Integer Functions ▪
• Mathematical Functions

Related Links

• MathWorld
• The Wolfram Functions Site
• An Elementary Introduction to the Wolfram Language : More about Numbers
• An Elementary Introduction to the Wolfram Language : Writing Good Code
• NKS|Online (A New Kind of Science)

History

Introduced in 1996 (3.0) | Updated in 1999 (4.0) ▪ 2000 (4.1) ▪ 2002 (4.2)

Wolfram Research (1996), Fibonacci, Wolfram Language function, https://reference.wolfram.com/language/ref/Fibonacci.html (updated 2002).

Text

Wolfram Research (1996), Fibonacci, Wolfram Language function, https://reference.wolfram.com/language/ref/Fibonacci.html (updated 2002).

CMS

Wolfram Language. 1996. "Fibonacci." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2002. https://reference.wolfram.com/language/ref/Fibonacci.html.

APA

Wolfram Language. (1996). Fibonacci. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/Fibonacci.html

BibTeX

@misc{reference.wolfram_2025_fibonacci, author="Wolfram Research", title="{Fibonacci}", year="2002", howpublished="\url{https://reference.wolfram.com/language/ref/Fibonacci.html}", note=[Accessed: 17-June-2025 ]}

BibLaTeX

@online{reference.wolfram_2025_fibonacci, organization={Wolfram Research}, title={Fibonacci}, year={2002}, url={https://reference.wolfram.com/language/ref/Fibonacci.html}, note=[Accessed: 17-June-2025 ]}