GeneralizedLinearModelFit: GLM—Wolfram Documentation (original) (raw)
BUILT-IN SYMBOL
GeneralizedLinearModelFit
GeneralizedLinearModelFit[{{x1,y1},{x2,y2},…},{f1,f2,…},x]
constructs a generalized linear model of the form 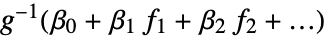 that fits the yi for each xi.
that fits the yi for each xi.
GeneralizedLinearModelFit[data,{f1,f2,…},{x1,x2,…}]
constructs a generalized linear model of the form 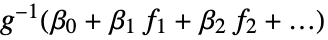 where the fi depend on the variables xk.
where the fi depend on the variables xk.
Details and Options
- GeneralizedLinearModelFit attempts to model the input data using a linear combination of functions transformed by a generic invertible function (link function).
- GeneralizedLinearModelFit produces a generalized linear model of the form
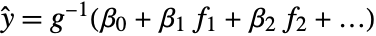 under the assumption that the original
under the assumption that the original 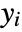 are independent observations following an exponential family distribution with mean
are independent observations following an exponential family distribution with mean 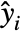 and the function
and the function 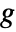 being an invertible link function.
being an invertible link function. - The ExponentialFamily option controls the distribution while the LinkFunction option controls the form of
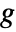 .
. - GeneralizedLinearModelFit returns a symbolic FittedModel object to represent the generalized linear model it constructs. The properties and diagnostics of the model can be obtained from model["property"].
- The value of the best-fit function from GeneralizedLinearModelFit at a particular point x1, … can be found from model[x1,…].
- Possible forms of data are:
{y1,y2,…} equivalent to the form {{1,y1},{2,y2},…} {{x11,x12,…,y1},…} a list of independent values xij and the responses yi {{x11,x12,…}y1,…} a list of rules between input values and response {{x11,x12,…},…}{y1,y2,…} a rule between a list of input values and responses {{x11,…,y1,…},…}n fit the n 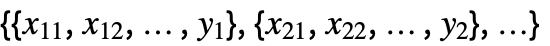 column of a matrix
column of a matrixTabular[…]name fit the column name in a tabular object - With multivariate data such as
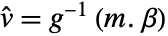 , the number of coordinates xi1, xi2, … should equal the number of variables xi.
, the number of coordinates xi1, xi2, … should equal the number of variables xi. - Additionally, data can be specified using a design matrix without specifying functions and variables:
{m,v} a design matrix m and response vector v - In GeneralizedLinearModelFit[m,v], the design matrix m is formed from the values of basis functions fi at data points in the form {{f1,f2,…},{f1,f2,…},…}. The response vector v is the list of responses {y1,y2,…}.
- For a design matrix m and response vector v, the model is
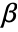 , where
, where 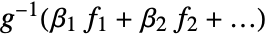 is the vector of parameters to be estimated.
is the vector of parameters to be estimated. - When a design matrix is used, the basis functions fi can be specified using the form GeneralizedLinearModelFit[{m,v},{f1,f2,…}].
- GeneralizedLinearModelFit takes the following options:
AccuracyGoal Automatic the accuracy sought ConfidenceLevel 95/100 confidence level for parameters and predictions CovarianceEstimatorFunction "ExpectedInformation" estimation method for the parameter covariance matrix DispersionEstimatorFunction Automatic function for estimating the dispersion parameter ExponentialFamily Automatic exponential family distribution for y IncludeConstantBasis True whether to include a constant basis function LinearOffsetFunction None known offset in the linear predictor LinkFunction Automatic link function for the model MaxIterations Automatic maximum number of iterations to use NominalVariables None variables considered as nominal PrecisionGoal Automatic the precision sought Weights Automatic weights for data elements WorkingPrecision Automatic the precision for internal computations - With the setting IncludeConstantBasis->False, a model of the form
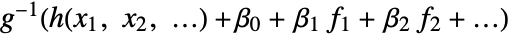 is fitted.
is fitted. - With the setting LinearOffsetFunction->h, a model of the form
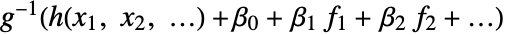 is fitted.
is fitted. - With ConfidenceLevel->p, probability-p confidence intervals are computed for parameter and prediction intervals.
- With the setting DispersionEstimatorFunction->f, the common dispersion is estimated by f[y,
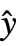 ,w] where y={y1,y2,…} is the list of observations,
,w] where y={y1,y2,…} is the list of observations, 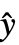 ={
={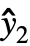 ,
,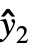 ,…} is the list of predicted values, and w={w1,w2,…} is the list of weights for the measurements yi.
,…} is the list of predicted values, and w={w1,w2,…} is the list of weights for the measurements yi. - Possible settings for ExponentialFamily include: "Gaussian", "Binomial", "Poisson", "Gamma", "InverseGaussian", or "QuasiLikelihood".
Properties
- Properties related to data and the fitted function obtained using model["property"] include:
"BasisFunctions" list of basis functions "BestFit" fitted function "BestFitParameters" parameter estimates "Data" the input data or design matrix and response vector "DesignMatrix" design matrix for the model "Function" best fit pure function "LinearPredictor" fitted linear combination "Response" response values in the input data "Weights" weights used to fit the data - Properties related to dispersion and model deviances include:
"Deviances" deviances "DevianceData" deviance table dataset "EstimatedDispersion" estimated dispersion parameter "NullDeviance" deviance for the null model "NullDegreesOfFreedom" degrees of freedom for the null model "ResidualDeviance" difference between the deviance for the fitted model and the deviance for the full model "ResidualDegreesOfFreedom" difference between the model degrees of freedom and null degrees of freedom - Types of residuals include:
"AnscombeResiduals" Anscombe residuals "DevianceResiduals" deviance residuals "FitResiduals" difference between actual and predicted responses "LikelihoodResiduals" likelihood residuals "PearsonResiduals" Pearson residuals "StandardizedDevianceResiduals" standardized deviance residuals "StandardizedPearsonResiduals" standardized Pearson residuals "WorkingResiduals" working residuals - Properties and diagnostics for parameter estimates include:
"CorrelationMatrix" asymptotic parameter correlation matrix "CovarianceMatrix" asymptotic parameter covariance matrix "ParameterEstimates" table of fitted parameter information - Properties related to influence measures include:
"CookDistances" list of Cook distances "HatDiagonal" diagonal elements of the hat matrix - Properties of predicted values include:
"PredictedResponse" fitted values for the data - Properties that measure goodness of fit include:
"AdjustedLikelihoodRatioIndex" Ben‐Akiva and Lerman's adjusted likelihood ratio index "AIC" Akaike Information Criterion "BIC" Bayesian Information Criterion "CoxSnellPseudoRSquared" Cox and Snell's pseudo 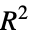
"CraggUhlerPseudoRSquared" Cragg and Uhler's pseudo 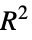
"EfronPseudoRSquared" Efron's pseudo 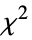
"LikelihoodRatioIndex" McFadden's likelihood ratio index "LikelihoodRatioStatistic" likelihood ratio "LogLikelihood" log likelihood for the fitted model "PearsonChiSquare" Pearson's 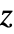 statistic
statistic
Examples
open allclose all
Basic Examples (1)
Define a dataset:
Fit a log-linear Poisson model to the data:
See the functional forms of the model:
Evaluate the model at a point:
Plot the data points and the models:
Compute and plot the deviance residuals for the model:
Scope (15)
Data (8)
Fit data with success probability responses, assuming increasing integer-independent values:
This is equivalent to:
Fit a model of more than one variable:
Fit data to a linear combination of functions of predictor variables:
Fit a list of rules:
Fit a rule of input values and responses:
Specify a column as the response:
Fit a model with categorical predictor variables:
Obtain a deviance table for the model:
Fit a model given a design matrix and response vector:
See the functional form:
Fit the model referring to the basis functions as x and y:
Obtain a list of available properties for a generalized linear model:
Properties (7)
Data & Fitted Functions (1)
Fit a generalized linear model:
Extract the original data:
Obtain and plot the best fit:
Obtain the fitted function as a pure function:
Get the design matrix and response vector for the fitting:
Residuals (1)
Examine residuals for a fit:
Visualize the raw residuals:
Visualize Anscombe residuals and standardized Pearson residuals in stem plots:
Dispersion and Deviances (1)
Fit a gamma regression model to some data:
Obtain the estimated dispersion:
Plot the deviances for each point:
Get a dataset of the deviance table:
Get the residual deviances from the table:
Parameter Estimation Diagnostics (1)
Obtain a formatted table of parameter information:
Extract the column of 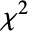 -statistic values:
-statistic values:
Influence Measures (1)
Fit some data containing extreme values to a logit model:
Check Cook distances to identify highly influential points:
Check the diagonal elements of the hat matrix to assess influence of points on the fitting:
Prediction Values (1)
Fit an inverse Gaussian model:
Plot the predicted values against the observed values:
Goodness-of-Fit Measures (1)
Obtain a table of goodness-of-fit measures for a log-linear Poisson model:
Compute goodness-of-fit measures for all subsets of predictor variables:
Rank the models by AIC:
Generalizations & Extensions (1)
Perform other mathematical operations on the functional form of the model:
Integrate symbolically and numerically:
Find a predictor value that gives a particular value for the model:
Options (10)
ConfidenceLevel (1)
The default gives 95% confidence intervals:
Use 99% intervals instead:
Set the level to 90% within FittedModel:
CovarianceEstimatorFunction (1)
Fit a generalized linear model:
Compute the covariance matrix using the expected information matrix:
Use the observed information matrix instead:
DispersionEstimatorFunction (1)
Fit a binomial model:
Compute the covariance matrix:
Compute the covariance matrix estimating the dispersion by Pearson's  :
:
ExponentialFamily (1)
Fit data to a simple linear regression model:
Fit to a canonical gamma regression model:
Fit to a canonical inverse Gaussian regression model:
IncludeConstantBasis (1)
Fit a simple linear regression model:
Fit the linear model with intercept zero:
LinearOffsetFunction (1)
Fit data to a canonical gamma regression model:
Fit data to a gamma regression model with a known Sqrt[x] term:
LinkFunction (1)
Fit a Poisson model with canonical Log link:
Use a named link:
Use a pure function for a shifted Sqrt link:
NominalVariables (1)
Fit the data treating the first variable as a nominal variable:
Treat both variables as nominal:
Weights (1)
Fit a model using equal weights:
Give explicit weights for the data points:
WorkingPrecision (1)
Use WorkingPrecision to get higher precision in parameter estimates:
Obtain the fitted function:
Reduce the precision in property computations after the fitting:
Applications (2)
Simulate some probability data:
Fit and visually compare binomial generalized linear models with a variety of link functions:
Fit count data from a contingency table to a Poisson log-linear model:
Display counts, predicted values, and standardized residuals in a tabular form:
Properties & Relations (5)
Related Guides
▪
- Statistical Model Analysis ▪
- Statistical Data Analysis ▪
- Scientific Data Analysis ▪
- Numerical Data ▪
- Matrix-Based Minimization ▪
- Tabular Modeling ▪
- Supervised Machine Learning
Wolfram Research (2008), GeneralizedLinearModelFit, Wolfram Language function, https://reference.wolfram.com/language/ref/GeneralizedLinearModelFit.html (updated 2025).
Text
Wolfram Research (2008), GeneralizedLinearModelFit, Wolfram Language function, https://reference.wolfram.com/language/ref/GeneralizedLinearModelFit.html (updated 2025).
CMS
Wolfram Language. 2008. "GeneralizedLinearModelFit." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2025. https://reference.wolfram.com/language/ref/GeneralizedLinearModelFit.html.
APA
Wolfram Language. (2008). GeneralizedLinearModelFit. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/GeneralizedLinearModelFit.html
BibTeX
@misc{reference.wolfram_2025_generalizedlinearmodelfit, author="Wolfram Research", title="{GeneralizedLinearModelFit}", year="2025", howpublished="\url{https://reference.wolfram.com/language/ref/GeneralizedLinearModelFit.html}", note=[Accessed: 05-May-2025 ]}
BibLaTeX
@online{reference.wolfram_2025_generalizedlinearmodelfit, organization={Wolfram Research}, title={GeneralizedLinearModelFit}, year={2025}, url={https://reference.wolfram.com/language/ref/GeneralizedLinearModelFit.html}, note=[Accessed: 05-May-2025 ]}