MinValue—Wolfram Language Documentation (original) (raw)
BUILT-IN SYMBOL
MinValue
MinValue[f,x]
gives the minimum value of f with respect to x.
MinValue[f,{x,y,…}]
gives the exact minimum value of f with respect to x, y, ….
MinValue[{f,cons},{x,y,…}]
gives the minimum value of f subject to the constraints cons.
MinValue[…,x∈rdom]
constrains x to be in the region or domain rdom.
Details and Options
- MinValue is also known as infimum.
- MinValue finds the global minimum of f subject to the constraints given.
- MinValue is typically used to find the smallest possible values given constraints. In different areas, this may be called the best strategy, best fit, best configuration and so on.
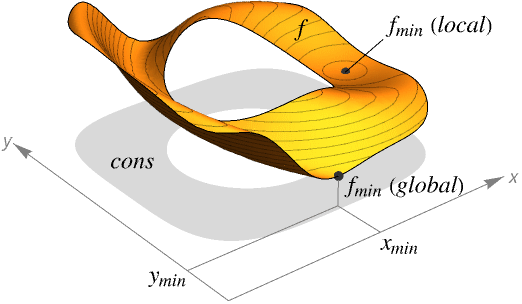
- If f and cons are linear or polynomial, MinValue will always find the global infimum.
- The constraints cons can be any logical combination of:
lhs==rhs equations lhs>rhs, lhs≥rhs, lhs<rhs, lhs≤rhs inequalities (LessEqual,…) lhsrhs, lhsrhs, lhsrhs, lhsrhs vector inequalities (VectorLessEqual,…) Exists[…], ForAll[…] quantified conditions {x,y,…}∈rdom region or domain specification - MinValue[{f,cons},x∈rdom] is effectively equivalent to MinValue[{f,cons∧x∈rdom},x].
- For x∈rdom, the different coordinates can be referred to using Indexed[x,i].
- Possible domains rdom include:
Reals real scalar variable Integers integer scalar variable Vectors[n,dom] vector variable in 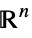
Matrices[{m,n},dom] matrix variable in 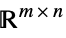
ℛ vector variable restricted to the geometric region 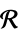
- By default, all variables are assumed to be real.
- MinValue will return exact results if given exact input. With approximate input, it automatically calls NMinValue.
- MinValue will return the following forms:
fmin finite minimum ∞ infeasible, i.e. the constraint set is empty -∞ unbounded, i.e. the values of f can be arbitrarily small - MinValue gives the infimum of values of f. It may not be attained for any values of x, y, ….
- N[MinValue[…]] calls NMinValue for optimization problems that cannot be solved symbolically.
Examples
open allclose all
Basic Examples (5)
Find the minimum value of a univariate function:
Find the minimum value of a multivariate function:
Find the minimum value of a function subject to constraints:
Find the minimum value as a function of parameters:
Find the minimum value of a function over a geometric region:
Scope (36)
Basic Uses (7)
Minimize 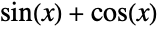 over the unconstrained reals:
over the unconstrained reals:
Minimize 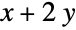 subject to constraints
subject to constraints 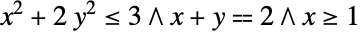 :
:
Constraints may involve arbitrary logical combinations:
An unbounded problem:
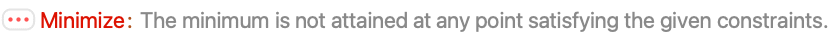
An infeasible problem:

The infimum value may not be attained:
Use a vector variable and a vector inequality:
Univariate Problems (7)
Unconstrained univariate polynomial minimization:
Constrained univariate polynomial minimization:
Exp-log functions:
Analytic functions over bounded constraints:

Periodic functions:
Combination of trigonometric functions with commensurable periods:
Combination of periodic functions with incommensurable periods:
Piecewise functions:
Unconstrained problems solvable using function property information:
Multivariate Problems (9)
Multivariate linear constrained minimization:
Linear-fractional constrained minimization:
Unconstrained polynomial minimization:
Constrained polynomial optimization can always be solved:
The minimum value may not be attained:
The objective function may be unbounded:
There may be no points satisfying the constraints:

Quantified polynomial constraints:
Algebraic minimization:
Bounded transcendental minimization:
Piecewise minimization:
Convex minimization:
Minimize convex objective function 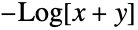 such that
such that 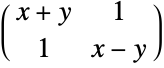 is positive semidefinite and
is positive semidefinite and 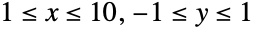 :
:
Plot the function and the minimum value over the region:
Parametric Problems (4)
Parametric linear optimization:
The minimum value is a continuous function of parameters:
Parametric quadratic optimization:
The minimum value is a continuous function of parameters:
Unconstrained parametric polynomial minimization:
Constrained parametric polynomial minimization:
Optimization over Integers (3)
Univariate problems:
Integer linear programming:
Polynomial minimization over the integers:
Optimization over Regions (6)
Find the minimum value of a function over a geometric region:
Plot it:
Find the minimum distance between two regions:
Plot it:
Find the minimum 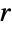 such that the triangle and ellipse still intersect:
such that the triangle and ellipse still intersect:
Plot it:
Find the minimum radius of a disk that contains the given three points:
Using Circumsphere gives the same result directly:
Use 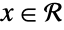 to specify that
to specify that 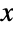 is a vector in
is a vector in 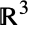 :
:
Find the minimum distance between two regions:
Plot it:
Options (1)
WorkingPrecision (1)
Finding the exact minimum takes a long time:
With WorkingPrecision->100, the result is an exact minimum value, but it might be incorrect:
Applications (9)
Basic Applications (3)
Find the minimal perimeter among rectangles with a unit area:
Find the minimal perimeter among triangles with a unit area:
Find the distance to a parabola from a point on its axis:
Assuming a particular relationship between the 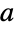 and
and 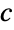 parameters:
parameters:
Geometric Distances (6)
The distance of a point p to a region ℛ is given by MinValue[EuclideanDistance[p,q],q∈ℛ]. Find the distance of {1,1} to the unit Disk[]:
Plot it:
Find the distance of the point {1,3/4} to the standard unit simplex Simplex[2]:
Plot it:
Find the distance of the point {1,1,1} to the standard unit sphere Sphere[]:
Plot it:
Find the distance of the point {-1/3,1/3,1/3} to the standard unit simplex Simplex[3]:
Plot it:
The distance between regions and can be found through MinValue[EuclideanDistance[p,q],{p∈,q∈}]. Find the distance between Disk[{0,0}] and Rectangle[{3,3}]:
Find the distance between Line[{{0,0,0},{1,1,1}}] and Ball[{5,5,0},1]:
Properties & Relations (5)
Minimize gives both the value of the minimum and the minimizer point:
MinValue gives an exact global minimum value of the objective function:
NMinValue attempts to find a global minimum numerically, but may find a local minimum:
FindMinValue finds local minima depending on the starting point:
MinValue can solve linear programming problems:
LinearProgramming can be used to solve the same problem given in matrix notation:
Use RegionDistance to compute the minimum distance from a point to a region:
Compute the distance using MinValue:
Use RegionBounds to compute the bounding box:
Use MaxValue and MinValue to compute the same bounds:
Possible Issues (1)
MinValue requires that all functions present in the input be real valued:
Values for which the equation is satisfied but the square roots are not real are disallowed:
Tech Notes
▪
- Symbolic Mathematics: Basic Operations ▪
- Inequalities ▪
- Minimization and Maximization ▪
- Constrained Optimization ▪
- Unconstrained Optimization ▪
- Implementation notes: Algebra and Calculus
Related Guides
▪
- Optimization ▪
- Solvers over Regions ▪
- Scientific Models ▪
- Discrete Calculus ▪
- Symbolic Vectors, Matrices and Arrays ▪
- Convex Optimization
Wolfram Research (2008), MinValue, Wolfram Language function, https://reference.wolfram.com/language/ref/MinValue.html (updated 2021).
Text
Wolfram Research (2008), MinValue, Wolfram Language function, https://reference.wolfram.com/language/ref/MinValue.html (updated 2021).
CMS
Wolfram Language. 2008. "MinValue." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2021. https://reference.wolfram.com/language/ref/MinValue.html.
APA
Wolfram Language. (2008). MinValue. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/MinValue.html
BibTeX
@misc{reference.wolfram_2025_minvalue, author="Wolfram Research", title="{MinValue}", year="2021", howpublished="\url{https://reference.wolfram.com/language/ref/MinValue.html}", note=[Accessed: 19-June-2025 ]}
BibLaTeX
@online{reference.wolfram_2025_minvalue, organization={Wolfram Research}, title={MinValue}, year={2021}, url={https://reference.wolfram.com/language/ref/MinValue.html}, note=[Accessed: 19-June-2025 ]}