Ordering—Wolfram Language Documentation (original) (raw)

BUILT-IN SYMBOL

• See Also
  • Sort
  • OrderingBy
  • SortBy
  • Max
  • Min
  • RankedMin
  • RankedMax
  • MaximalBy
  • MinimalBy
  • Position
  • OrderedQ
  • Median
  • Order
  • NumericalOrder
  • AlphabeticOrder
  • LexicographicOrder
• Related Guides
  • Math & Counting Operations on Lists
  • Permutations
  • Discrete Mathematics
  • Descriptive Statistics
  • Elements of Lists
  • Robust Descriptive Statistics
  • GPU Computing
  • GPU Computing with NVIDIA
• Tech Notes
  • Ordering in Lists
  • Structural Operations

Ordering

Ordering[list]

gives the positions in list at which each successive element of Sort[list] appears.

Ordering[list,n]

gives the positions in list at which the first n elements of Sort[list] appear.

Ordering[list,-n]

gives the positions of the last n elements of Sort[list].

Ordering[list,n,p]

gives positions in list of elements of Sort[list,p].

Details

• In a numerical list, Ordering[list,n] gives the positions of the n smallest elements. Ordering[list,-n] gives the positions of the n largest elements.
• If there are several smallest elements in list, Ordering[list,1] will give only the position of the one that appears first.
• list[[Ordering[list]]] is the same as Sort[list].
• Ordering[list,seq] is equivalent to Take[Ordering[list],seq].
• Ordering[list,UpTo[n]] returns n positions, or as many as are available.
• Ordering[list,All,p] gives the position at which all elements of list appear in Sort[list,p].
• Ordering can be used on expressions with any head, not only List.

Examples

open allclose all

Basic Examples (4)

Find the ordering that sorts a list:

Apply the ordering:

Find the positions of the 4 smallest elements in a list:

Find the position of the largest element:

Find the ordering of values in an Association:

Scope (4)

Find positions of elements from the 4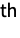 smallest to the largest:

Find positions of elements in Sort[list,Greater]:

Find the positions of the 6 smallest elements in a list, or as many as are available:

Find the ordering of rows in a Tabular object:

Generalizations & Extensions (1)

Use expressions with any head:

Applications (3)

Find a permutation that sorts a list:

Apply the permutation:

Find the inverse of a permutation:

Sort a list of lists with respect to a particular position:

The same as Sort, but Ordering keeps the original ordering when elements are the same:

Using Ordering this way is much faster for large sets of lists:

Properties & Relations (2)

Find the position of the maximum element:

list[[Ordering[list]]] is equivalent to Sort[list]:

Related Guides

▪

• Math & Counting Operations on Lists ▪
• Permutations ▪
• Discrete Mathematics ▪
• Descriptive Statistics ▪
• Elements of Lists ▪
• Robust Descriptive Statistics ▪
• GPU Computing ▪
• GPU Computing with NVIDIA

Wolfram Research (2000), Ordering, Wolfram Language function, https://reference.wolfram.com/language/ref/Ordering.html (updated 2015).

Text

Wolfram Research (2000), Ordering, Wolfram Language function, https://reference.wolfram.com/language/ref/Ordering.html (updated 2015).

CMS

Wolfram Language. 2000. "Ordering." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2015. https://reference.wolfram.com/language/ref/Ordering.html.

APA

Wolfram Language. (2000). Ordering. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/Ordering.html

BibTeX

@misc{reference.wolfram_2025_ordering, author="Wolfram Research", title="{Ordering}", year="2015", howpublished="\url{https://reference.wolfram.com/language/ref/Ordering.html}", note=[Accessed: 30-April-2025 ]}

BibLaTeX

@online{reference.wolfram_2025_ordering, organization={Wolfram Research}, title={Ordering}, year={2015}, url={https://reference.wolfram.com/language/ref/Ordering.html}, note=[Accessed: 30-April-2025 ]}