PermutationListQ—Wolfram Language Documentation (original) (raw)

BUILT-IN SYMBOL

• See Also
  • PermutationList
  • PermutationCycles
  • PermutationCyclesQ
• Related Guides
  • Permutations
• Tech Notes
  • Permutation Lists

PermutationListQ

Details

• A valid permutation list {p1,…,pn} is a rearrangement of the integers {1,…,n}.

Examples

open allclose all

Basic Examples (1)

A valid permutation list:

Invalid permutation lists:

Scope (2)

PermutationListQ works efficiently with large permutation lists:

The empty list is considered a permutation list of length and degree 0:

Properties & Relations (4)

RandomSample[Range[n]] always gives a valid permutation list:

A possible, but less efficient, Wolfram Language implementation:

Validity of permutations in cyclic form is checked with PermutationCyclesQ. A permutation list can always be obtained as a permutation of the elements in canonical order using Permute:

Ordering always returns a permutation list, even if the elements of the expression are repeated:

Neat Examples (1)

There are 409113 integer numbers up to 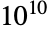whose decimal digits form permutation lists. This is how the first 153 (the largest being 54321) are distributed:

Wolfram Research (2010), PermutationListQ, Wolfram Language function, https://reference.wolfram.com/language/ref/PermutationListQ.html.

Text

Wolfram Research (2010), PermutationListQ, Wolfram Language function, https://reference.wolfram.com/language/ref/PermutationListQ.html.

CMS

Wolfram Language. 2010. "PermutationListQ." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/PermutationListQ.html.

APA

Wolfram Language. (2010). PermutationListQ. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/PermutationListQ.html

BibTeX

@misc{reference.wolfram_2025_permutationlistq, author="Wolfram Research", title="{PermutationListQ}", year="2010", howpublished="\url{https://reference.wolfram.com/language/ref/PermutationListQ.html}", note=[Accessed: 17-June-2025 ]}

BibLaTeX

@online{reference.wolfram_2025_permutationlistq, organization={Wolfram Research}, title={PermutationListQ}, year={2010}, url={https://reference.wolfram.com/language/ref/PermutationListQ.html}, note=[Accessed: 17-June-2025 ]}