Function defined in pieces for different conditions—Wolfram Documentation (original) (raw)

• See Also
  • PiecewiseExpand
  • $MaxPiecewiseCases
  • Boole
  • Max
  • Min
  • RealAbs
  • Abs
  • RealSign
  • Sign
  • Clip
  • Ramp
  • UnitStep
  • UnitBox
  • UnitTriangle
  • Floor
  • Ceiling
  • Round
  • IntegerPart
  • Mod
  • SquareWave
  • TriangleWave
  • BezierFunction
  • BSplineFunction
  • Which
  • If

  • ---

  • Characters
  • \[Piecewise]
• Related Guides
  • Numerical Functions
  • Conditionals
  • Inequalities
  • Elementary Functions
• Tech Notes
  • Piecewise Functions
  • Conditionals
• • See Also
    * PiecewiseExpand
    * $MaxPiecewiseCases
    * Boole
    * Max
    * Min
    * RealAbs
    * Abs
    * RealSign
    * Sign
    * Clip
    * Ramp
    * UnitStep
    * UnitBox
    * UnitTriangle
    * Floor
    * Ceiling
    * Round
    * IntegerPart
    * Mod
    * SquareWave
    * TriangleWave
    * BezierFunction
    * BSplineFunction
    * Which
    * If
    * ---
    * Characters
    * \[Piecewise]
  • Related Guides
    * Numerical Functions
    * Conditionals
    * Inequalities
    * Elementary Functions
  • Tech Notes
    * Piecewise Functions
    * Conditionals

Piecewise[{{val1,cond1},{val2,cond2},…}]

represents a piecewise function with values vali in the regions defined by the conditions condi.

Piecewise[{{val1,cond1},…},val]

uses default value val if none of the condi apply. The default for val is 0.

Details

• The condi are typically inequalities such as .
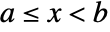• The condi are evaluated in turn, until one of them is found to yield True.
• If all preceding condi yield False, then the vali corresponding to the first condi that yields True is returned as the value of the piecewise function.
• If any of the preceding condi do not literally yield False, the Piecewise function is returned in symbolic form.
• Only those vali explicitly included in the returned form are evaluated.
• Elements of the form {vali,False} are dropped, as are all elements after the first {vali,True}.
• Piecewise[conds] automatically evaluates to Piecewise[conds,0].
• Piecewise can be used in such functions as Integrate, Minimize, Reduce, DSolve, and Simplify, as well as their numeric analogs.
• Piecewise[{{v1,c1},{v2,c2},…}] can be input in the form 

  v1	c1
  v2	c2
  …
  . The piecewise operator  can be entered as pw or \[Piecewise]. The grid of values and conditions can be constructed by first entering , then using and .

• In StandardForm and TraditionalForm, Piecewise[{{v1,c1},{v2,c2},…}] is normally output using a brace, as in 

  v1	c1
  v2	c2
  …
  .

Examples

open all close all

Basic Examples (3)

Set up a piecewise function with different pieces below and above zero:

Find the derivative of a piecewise function:

Use pw to enter  and and then for each additional piecewise case:

Scope (12)

Define a piecewise function:

Evaluate it at specific points:

Plot it:

Refine it under assumptions:

Automatic simplification of Piecewise functions:

Remove unreachable cases:

Remove False conditions:

Merge cases with the same values:

If values are not specified in a region, they are assumed to be zero:

This specifies that the default value should be 1:

Compute limits of piecewise functions:

Compute the limit in the direction of the positive imaginary axis:

Compute the series of a piecewise function:

Integrate a piecewise function:

Integration constants are chosen to make the result continuous:

Compute a definite integral of a piecewise function:

Laplace transform of a piecewise function:

Solve a piecewise differential equation:

Reduce a piecewise equation:

Integrating an implicitly piecewise integrand can give an explicit Piecewise result:

Symbolic minimization can give piecewise functions:

Applications (1)

Compute the volume of an ellipsoid:

Properties & Relations (11)

PiecewiseExpand converts nested piecewise functions into a single piecewise function:

Min, Max, UnitStep, and Clip are piecewise functions of real arguments:

Abs, Sign, and Arg are piecewise functions when their arguments are assumed to be real:

KroneckerDelta and DiscreteDelta are piecewise functions of complex arguments:

Boole is a piecewise function of a Boolean argument:

If, Which, and Switch can be interpreted as piecewise functions:

Convert Floor, Ceiling, Round, IntegerPart, and FractionalPart for finite ranges:

Convert Mod and Quotient when the number of cases is finite:

UnitBox and UnitTriangle are piecewise functions of real arguments:

Convert SquareWave, TriangleWave, and SawtoothWave for finite ranges:

BernsteinBasis and BSplineBasis are piecewise functions of real arguments:

Possible Issues (1)

Derivatives are computed piece-by-piece, unless the function is univariate in a real variable:

To specify that 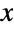is real, use inequalities in the first condition:

This function is discontinuous at :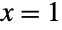

Wolfram Research (2004), Piecewise, Wolfram Language function, https://reference.wolfram.com/language/ref/Piecewise.html (updated 2008).

Text

Wolfram Research (2004), Piecewise, Wolfram Language function, https://reference.wolfram.com/language/ref/Piecewise.html (updated 2008).

CMS

Wolfram Language. 2004. "Piecewise." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2008. https://reference.wolfram.com/language/ref/Piecewise.html.

APA

Wolfram Language. (2004). Piecewise. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/Piecewise.html

BibTeX

@misc{reference.wolfram_2025_piecewise, author="Wolfram Research", title="{Piecewise}", year="2008", howpublished="\url{https://reference.wolfram.com/language/ref/Piecewise.html}", note=[Accessed: 22-October-2025]}

BibLaTeX

@online{reference.wolfram_2025_piecewise, organization={Wolfram Research}, title={Piecewise}, year={2008}, url={https://reference.wolfram.com/language/ref/Piecewise.html}, note=[Accessed: 22-October-2025]}