Resolve—Wolfram Language Documentation (original) (raw)

BUILT-IN SYMBOL

Resolve

Resolve[expr]

attempts to resolve expr into a form that eliminates ForAll and Exists quantifiers.

Details and Options

Examples

open allclose all

Basic Examples (4)

Prove that the unit disk is nonempty:

Find the conditions for a quadratic form over the reals to be positive:

Find conditions for a quadratic to have at least two distinct complex roots:

Find the projection of a geometric region:

Scope (52)

Complex Domain (6)

Decide the existence of solutions of a univariate polynomial equation:

Decide the existence of solutions of a multivariate polynomial system:

Decide the truth value of fully quantified polynomial formulas:

Find conditions under which a polynomial equation has solutions:

Find conditions under which a polynomial system has solutions:

Find conditions under which a quantified polynomial formula is true:

Real Domain (18)

Decide the existence of solutions of a univariate polynomial equation:

Decide the existence of solutions of a univariate polynomial inequality:

Decide the existence of solutions of a multivariate polynomial system:

Decide the truth value of fully quantified polynomial formulas:

Decide the existence of solutions of an exp-log equation:

Decide the existence of solutions of an exp-log inequality:

Decide the existence of solutions of an elementary function equation in a bounded interval:

Decide the existence of solutions of a holomorphic function equation in a bounded interval:

Decide the existence of solutions of a periodic elementary function equation:

Fully quantified formulas exp-log in the first variable and polynomial in the other variables:

Fully quantified formulas elementary and bounded in the first variable:

Fully quantified formulas holomorphic and bounded in the first variable:

Find conditions under which a linear system has solutions:

Find conditions under which a quadratic system has solutions:

Find conditions under which a polynomial system has solutions:

Find conditions under which a formula linear in quantified variables is true:

Find conditions under which a formula quadratic in quantified variables is true:

Find conditions under which a quantified polynomial formula is true:

Integer Domain (10)

Decide the existence of solutions of a linear system of equations:

Decide the existence of solutions of a linear system of equations and inequalities:

Decide the existence of solutions of a univariate polynomial equation:

Decide the existence of solutions of a univariate polynomial inequality:

Decide the existence of solutions of Frobenius equations:

Decide the existence of solutions of binary quadratic equations:

Decide the existence of solutions of a Thue equation:

Decide the existence of solutions of a sum of squares equation:

Decide the existence of solutions of a bounded system of equations and inequalities:

Decide the existence of solutions of a system of congruences:

Boolean Domain (2)

Decide the satisfiability of a Boolean formula:

Find conditions under which a quantified Boolean formula is true:

Finite Field Domains (5)

Decide the existence of solutions of univariate equations:

Verify that a univariate equation is satisfied by all field elements:

Decide the existence of solutions of systems of linear equations:

Decide the existence of solutions of systems of polynomial equations:

Eliminate quantifiers:

Mixed Domains (3)

Decide the existence of solutions of an equation involving a real and a complex variable:

Decide the existence of solutions of an inequality involving Abs[x]:

Find under what conditions a fourth power of a complex number is real:

Geometric Regions (8)

Test :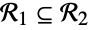

Get conditions for :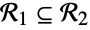

Project a cone to the 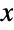- 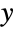plane:

Plot it:

An implicitly defined region:

A parametrically defined region:

Derived regions:

Plot it:

Regions dependent on parameters:

The conditions on 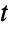indicate when the line intersects the circle:

A condition for :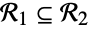

The condition tells when :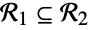

Vector variables:

Options (4)

Backsubstitution (1)

Here the solutions for x are expressed in terms of y:

With Backsubstitution->True, Resolve gives explicit numeric values for x:

Cubics (1)

By default, Resolve does not use general formulas for solving cubics in radicals:

With Cubics->True, Resolve expresses roots of cubics in terms of radicals:

Quartics (1)

By default, Resolve does not use general formulas for solving quartics in radicals:

With Quartics->True, Resolve expresses roots of quartics in terms of radicals:

WorkingPrecision (1)

This computation takes a long time due to high degrees of algebraic numbers involved:

With WorkingPrecision->100 you get an answer faster, but it may be incorrect:

Applications (9)

Polynomials (2)

Find conditions for a quintic to have all roots equal:

Find conditions for a quadratic to be always positive:

Theorem Proving (3)

Prove the inequality between the arithmetic mean and the geometric mean:

Prove a special case of Hölder's inequality:

Prove a special case of Minkowski's inequality:

Geometry (4)

The region 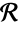is a subset o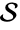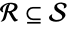f , if 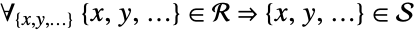is true. Show that Disk[{0,0},{2,1}] is a subset of Rectangle[{-2,-1},{2,1}]:

Plot it:

Show that Cylinder[]⊆Ball[{0,0,0},2]:

Plot it:

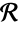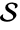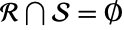A region is disjoint from if . Show that Circle[{0,0},2] and Disk[{0,0},1] are disjoint:

There are no points in the intersection, so they are disjoint:

Plot it:

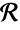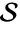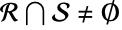A region intersects if . Show that Circle[{0,0},1] intersects Disk[{1/2,0},1]:

There are points in the intersection:

Plot it:

Properties & Relations (5)

For fully quantified systems of equations and inequalities, Resolve is equivalent to Reduce:

A solution instance can be found with FindInstance:

For systems with free variables, Resolve may return an unsolved system:

Reduce eliminates quantifiers and solves the resulting system:

Eliminate can be used to eliminate variables from systems of complex polynomial equations:

Resolve gives the same equations, but may also give inequations:

Find a formula description of a TransformedRegion:

Compute a formula description of 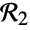using RegionMember:

Check that the formulas are equivalent:

Resolve shows that the polynomial 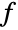is non-negative:

Use PolynomialSumOfSquaresList to represent 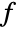as a sum of squares:

The Motzkin polynomial is non-negative, but is not a sum of squares:

Possible Issues (1)

Because x appears in an inequality, it is assumed to be real:

This allows complex values of x for which both sides of the inequality are real:

▪

Wolfram Research (2003), Resolve, Wolfram Language function, https://reference.wolfram.com/language/ref/Resolve.html (updated 2024).

Text

Wolfram Research (2003), Resolve, Wolfram Language function, https://reference.wolfram.com/language/ref/Resolve.html (updated 2024).

CMS

Wolfram Language. 2003. "Resolve." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2024. https://reference.wolfram.com/language/ref/Resolve.html.

APA

Wolfram Language. (2003). Resolve. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/Resolve.html

BibTeX

@misc{reference.wolfram_2025_resolve, author="Wolfram Research", title="{Resolve}", year="2024", howpublished="\url{https://reference.wolfram.com/language/ref/Resolve.html}", note=[Accessed: 02-May-2025 ]}

BibLaTeX

@online{reference.wolfram_2025_resolve, organization={Wolfram Research}, title={Resolve}, year={2024}, url={https://reference.wolfram.com/language/ref/Resolve.html}, note=[Accessed: 02-May-2025 ]}