SquareMatrixQ—Wolfram Language Documentation (original) (raw)

BUILT-IN SYMBOL

• See Also
  • MatrixQ
  • HermitianMatrixQ
  • VectorQ
  • Dimensions
  • SquareRepeatingElement
• Related Guides
  • Matrix Predicates
• Tech Notes
  • Scalars, Vectors, and Matrices

SquareMatrixQ

Details

• A matrix m is square if it has the same number of rows and columns, in which case Dimensions[m]{n,n}. »
• SquareMatrixQ works for symbolic as well as numerical matrices.

Examples

open allclose all

Basic Examples (3)

Test if an object is a square matrix:

The following matrix is not square:

These are not matrices:

Scope (9)

Basic Uses (5)

Test if a real machine-precision matrix is square:

Test if a complex matrix is square:

Test if an exact matrix is square:

Make the matrix square:

Use SquareMatrixQ with a symbolic matrix:

SquareMatrixQ works efficiently with large numerical matrices:

Special Matrices (4)

Applications (1)

Define a function that only evaluates for explicit square matrices:

This represents the Hermitian part of a matrix explicitly:

This does not evaluate because the matrix is rectangular:

This does not evaluate because a is not an explicit matrix:

Properties & Relations (5)

For a square matrix m, Dimensions[m] gives {n,n}:

SquareMatrixQ[expr] returns False for expressions that are not matrices:

The empty list is not considered a square matrix:

A square matrix is made up of 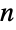vectors of length :

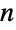Make sure it is made up of vectors:

Verify that all vectors have the same length and the number of vectors equals their length:

Hence m is a square matrix:

For lists, SquareMatrixQ[a] is equivalent to MatchQ[TensorDimensions[a],{n,n}]:

Wolfram Research (2014), SquareMatrixQ, Wolfram Language function, https://reference.wolfram.com/language/ref/SquareMatrixQ.html.

Text

Wolfram Research (2014), SquareMatrixQ, Wolfram Language function, https://reference.wolfram.com/language/ref/SquareMatrixQ.html.

CMS

Wolfram Language. 2014. "SquareMatrixQ." Wolfram Language & System Documentation Center. Wolfram Research. https://reference.wolfram.com/language/ref/SquareMatrixQ.html.

APA

Wolfram Language. (2014). SquareMatrixQ. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/SquareMatrixQ.html

BibTeX

@misc{reference.wolfram_2025_squarematrixq, author="Wolfram Research", title="{SquareMatrixQ}", year="2014", howpublished="\url{https://reference.wolfram.com/language/ref/SquareMatrixQ.html}", note=[Accessed: 20-June-2025 ]}

BibLaTeX

@online{reference.wolfram_2025_squarematrixq, organization={Wolfram Research}, title={SquareMatrixQ}, year={2014}, url={https://reference.wolfram.com/language/ref/SquareMatrixQ.html}, note=[Accessed: 20-June-2025 ]}