ControllableModelQ—Wolfram Language Documentation (original) (raw)
BUILT-IN SYMBOL
ControllableModelQ
Details and Options

Examples
open allclose all
Basic Examples (2)
A controllable system:
An uncontrollable system, since there is no way to affect the second state:
Scope (6)
Test the controllability of a system with approximate coefficients:
Exact coefficients:
Symbolic coefficients:
Multiple-input system:
Discrete-time system:
A descriptor system:
Controllability is equivalent to controllability of both slow and fast modes (C-controllability):
Test controllability of individual eigenmodes:
The system is uncontrollable because of eigenmode 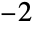 :
:
This can be seen in the Jordan form, where there is no way to affect the third state:
Test controllability of an AffineStateSpaceModel:
If an operating point 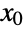 is given, controllability from
is given, controllability from 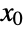 is tested:
is tested:
The system is controllable from a generic point:
Options (7)
Method (7)
By default, the controllability matrix is used for exact and symbolic systems:
The system is controllable if the ControllabilityMatrix has full rank:
The controllability Gramian is used for stable numeric systems:
The system is controllable if the ControllabilityGramian has full rank:
For the controllability Gramian, this is equivalent to it being positive definite:
The PBH rank test is used for all other numeric systems:
The system is controllable because 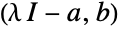 has full rank for all
has full rank for all 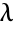 :
:
The controllability distribution is used for input-linear systems:
For linear systems, the tests based on the controllability matrix and distribution are equivalent:
Controllability of the linearized system implies controllability of the input-linear system:
The matrix test for input linear system uses the "Matrix" method for the linearized system:
Using no control input, the system follows the drift vector field 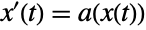 :
:
A system is weakly controllable if the drift vector field can also be used to move state:
Without including the drift vector field, the system is not controllable:
Applications (5)
The position and velocities of all three masses can be controlled by the force on 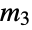 :
:
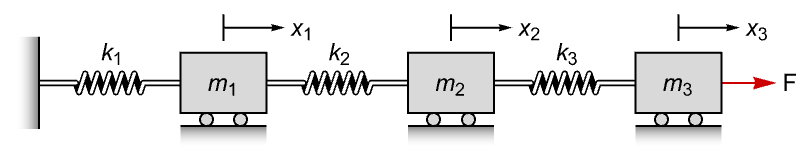
An electric circuit with the capacitor voltage and inductor current as states:
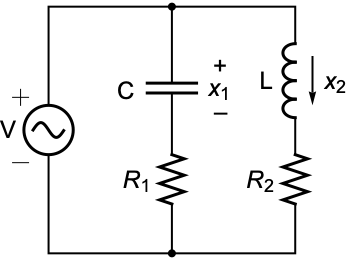
In general, the system is controllable:
However if 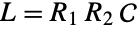 , it is not controllable:
, it is not controllable:
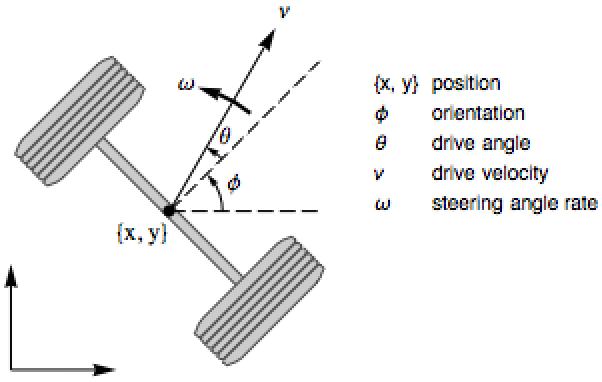
A unicycle with drive and steering as input:
The system is controllable, but the linearized system is not:
The parking problem:
The system is controllable, but the linearized system is not:
A rotating rigid satellite modeled using Euler's equations of motion:
Its controllability for various values of the principal moments and actuator combinations:
A grid to show the results:
If 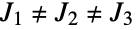 , the system is controllable with any two actuators:
, the system is controllable with any two actuators:
If 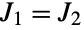 , the system is not controllable with actuators 1 and 2 or any one actuator:
, the system is not controllable with actuators 1 and 2 or any one actuator:
If 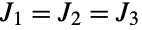 , the system is controllable only with all 3 actuators:
, the system is controllable only with all 3 actuators:
Properties & Relations (7)
A diagonal system is controllable, assuming  and
and 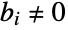 :
:
With  , there is no way to control the first state:
, there is no way to control the first state:
With 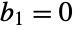 , the first state cannot be controlled directly, but indirectly from the second state:
, the first state cannot be controlled directly, but indirectly from the second state:
With 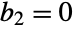 , the second state cannot be controlled directly or indirectly from the first state:
, the second state cannot be controlled directly or indirectly from the first state:
Use JordanModelDecomposition to compute the canonical state-space representation above:
Compute the controllability of each mode using the "PBH" test:
For descriptor systems, KroneckerModelDecomposition is the generalization of the diagonal form:
Determine the controllability of the slow subsystem from its structure:
Compute it using the original system:
Determine the controllability of the fast subsystem:
Compute it using the original system:
If the descriptor matrix of a StateSpaceModel has full rank, there is no fast subsystem:
Hence the complete controllability of the system can be evaluated from the slow subsystem:
Controllability is invariant under a nonsingular StateSpaceTransform:
Controllability is invariant under state feedback:
Compute the state feedback using StateFeedbackGains:
The closed-loop system is also controllable:
Controllability does not mean it is output controllable (OutputControllableModelQ):
Output controllability does not imply controllability:
Possible Issues (2)
The Gramian method is not reliable for systems that are not asymptotically stable:

The eigenvalue in the right half of the complex plane leads to instability for continuous-time systems:
For affine systems with nonzero drift, the distribution tests only for accessibility:
A random initial condition and random input signal generator:
Simulate the system 10 times with random inputs:
The system cannot be moved to the left of the initial point:
Wolfram Research (2010), ControllableModelQ, Wolfram Language function, https://reference.wolfram.com/language/ref/ControllableModelQ.html (updated 2014).
Text
Wolfram Research (2010), ControllableModelQ, Wolfram Language function, https://reference.wolfram.com/language/ref/ControllableModelQ.html (updated 2014).
CMS
Wolfram Language. 2010. "ControllableModelQ." Wolfram Language & System Documentation Center. Wolfram Research. Last Modified 2014. https://reference.wolfram.com/language/ref/ControllableModelQ.html.
APA
Wolfram Language. (2010). ControllableModelQ. Wolfram Language & System Documentation Center. Retrieved from https://reference.wolfram.com/language/ref/ControllableModelQ.html
BibTeX
@misc{reference.wolfram_2025_controllablemodelq, author="Wolfram Research", title="{ControllableModelQ}", year="2014", howpublished="\url{https://reference.wolfram.com/language/ref/ControllableModelQ.html}", note=[Accessed: 01-May-2025 ]}
BibLaTeX
@online{reference.wolfram_2025_controllablemodelq, organization={Wolfram Research}, title={ControllableModelQ}, year={2014}, url={https://reference.wolfram.com/language/ref/ControllableModelQ.html}, note=[Accessed: 01-May-2025 ]}