number 0 up to infinity (original) (raw)
"What's Special About This Number" Facts  eople have always been fascinated by NUMBERS... They are basic elements of mathematics used for counting, measuring, ranking, comparing quantities, and solving equations. Numbers have unique properties, and while some people see them as concise symbols manipulated according to arbitrary rules, others believe they carry occult powers and mystic virtues. The first known use of numbers dates back to around 30,000 BC when Stone Age people used simple tally marks, consisting of single strokes, to represent each additional unit. Each number is unique and has its own beauty. We have collected a vast array of facts pertaining to the magical world of numbers, covering different topics such as mathematics, history, philosophy, psychology, symbolism, etymology, language, and/or ethnology... eople have always been fascinated by NUMBERS... They are basic elements of mathematics used for counting, measuring, ranking, comparing quantities, and solving equations. Numbers have unique properties, and while some people see them as concise symbols manipulated according to arbitrary rules, others believe they carry occult powers and mystic virtues. The first known use of numbers dates back to around 30,000 BC when Stone Age people used simple tally marks, consisting of single strokes, to represent each additional unit. Each number is unique and has its own beauty. We have collected a vast array of facts pertaining to the magical world of numbers, covering different topics such as mathematics, history, philosophy, psychology, symbolism, etymology, language, and/or ethnology...  We're excited to announce that you can now purchase “Numberopedia: What's Special About This Number” by G. Sarcone in PDF format! With 189 pages filled with an incredible variety of fun facts on numbers (and their peculiar properties), both mathematical and cultural, as well as tantalizing problems and anecdotes, there is much to learn for everyone. After confirmation of your order, we will email you the code to access the corresponding download page. So don't wait any longer to dive into the world of numbers! Numberopedia (189 pages, pdf format): €11.00 We're excited to announce that you can now purchase “Numberopedia: What's Special About This Number” by G. Sarcone in PDF format! With 189 pages filled with an incredible variety of fun facts on numbers (and their peculiar properties), both mathematical and cultural, as well as tantalizing problems and anecdotes, there is much to learn for everyone. After confirmation of your order, we will email you the code to access the corresponding download page. So don't wait any longer to dive into the world of numbers! Numberopedia (189 pages, pdf format): €11.00 |
|
|---|---|
| If you got a distinctive fact about any number listed here you think Archimedes' Lab community might enjoy, why not post it here? |  Conoscete un numero con delle proprietà originali? Contattateci! Conoscete un numero con delle proprietà originali? Contattateci! |
 Connaissez-vous un nombre avec des propriétés étonnantes? Contactez-nous! Connaissez-vous un nombre avec des propriétés étonnantes? Contactez-nous! |
Number list: lista dei numeri (it), liste des nombres (fr), lista de números (es, por), Liste besonderer Zahlen (ger), getallen en getalverzamelingen (du), seznam čísel (cz), 數表 (ch), 数の一覧 (jap), список чисел (ru), שמות מספרים (he).  0-6 |
0-6 |  7-12 |
7-12 | 13-23 |
13-23 |  24-69 |
24-69 |  70-200 |
70-200 |  201-∞ |
201-∞ |  5H0P
5H0P
| NaN | NaN (Not a Number) is, in computing, a value (or symbol) that is usually produced as the result of an operation on invalid input operands, especially in floating-point calculations. NaNs are close to some undefined or inderterminate expressions in mathematics. In short, NaN is not really a number but a symbol that represents a numerical quantity whose magnitude cannot be determined by the operating system. This mainly occurs when infinity and zero are misused in expressions. =  -n = log (-n) = ln (-n) = 0 / 0 = 00 = 1∞ = ∞0 = ∞ / ∞ = ∞ / -∞ = -∞ / ∞ = -∞ / -∞ = 0 x ∞ = 0 x -∞ = (-∞) + ∞ = ∞ + (-∞) = ln |0| / ln | ±∞| = e_±∞ x ln | 0| = (m / ±∞) x (n / 0) if m
-n = log (-n) = ln (-n) = 0 / 0 = 00 = 1∞ = ∞0 = ∞ / ∞ = ∞ / -∞ = -∞ / ∞ = -∞ / -∞ = 0 x ∞ = 0 x -∞ = (-∞) + ∞ = ∞ + (-∞) = ln |0| / ln | ±∞| = e_±∞ x ln | 0| = (m / ±∞) x (n / 0) if m  ±∞ and n
±∞ and n  0 Not all indeterminate forms produce a NaN: for instance, the division 1/0 makes no sense in pure mathematics, but curiously enough in IEEE 754 this fraction is, by convention, equal to +∞ (hence 1/∞ = 0). Reality is, there are no answers for expressions such as n/0 or n/∞ (for n > 0). For n/0 the problem we are trying to solve is simply: n = 0 x A We cannot find any number for A since 0 x A = 0 for any whole number, rational number, real number, and so on. Regarding the fraction n/∞, if we admit that it is equal to 0 (when n is small but >0), then: 1 + n/∞ = 1, thus ∞ + n = ∞, and n = 0... Which contradicts n > 0. So, don't try to use infinity as a real number, you will get wrong answers! Infinity cannot be used directly, but we can use a limit: n/∞ is undefined, we do know however that n/x (with, say n = 1) approaches 0 as x approaches ∞:
0 Not all indeterminate forms produce a NaN: for instance, the division 1/0 makes no sense in pure mathematics, but curiously enough in IEEE 754 this fraction is, by convention, equal to +∞ (hence 1/∞ = 0). Reality is, there are no answers for expressions such as n/0 or n/∞ (for n > 0). For n/0 the problem we are trying to solve is simply: n = 0 x A We cannot find any number for A since 0 x A = 0 for any whole number, rational number, real number, and so on. Regarding the fraction n/∞, if we admit that it is equal to 0 (when n is small but >0), then: 1 + n/∞ = 1, thus ∞ + n = ∞, and n = 0... Which contradicts n > 0. So, don't try to use infinity as a real number, you will get wrong answers! Infinity cannot be used directly, but we can use a limit: n/∞ is undefined, we do know however that n/x (with, say n = 1) approaches 0 as x approaches ∞:  The infinite series ∑ = 1 - 1 + 1 - 1 + 1 - 1 + … , called Grandi's series, also written: ∞ ∑ (-1)n n_=0 is a divergent series, meaning that it lacks a sum in the usual sense... In fact, if you treat this series like a telescoping series and/or use different bracketing procedures to sum it, you may obtain contradictory results... ∑ = 1 - 1 + 1 - 1 + 1 - 1 + 1 - 1 + ... = ∑1 = (1-1) + (1-1) + (1-1) + (1-1) + ... = 0 ∑2 = 1 + (-1+1) + (-1+1) + (-1+1) + ... = 1 ∑3 = 1 + (1-1+1-1+1-1+ ...) = 1 + ∑ => ∑ = 1/2 As shown above, it appears to equal 0 and 1, yet in some sense 'sums' to 1/2, producing a paradox... The error here is that the associative law cannot be applied freely to an infinite sum unless the sum is absolutely convergent. We can say that the sum of Grandi's series is NaN. | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | |
| ----------------------------------------------------------------------------------------------------------------------------------------------------------- | ----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------- | ------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------- | ------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------- | -------------------------------------------------------------------------------------------------------------------------------------------------------------- | --------------------------------------------------------------------------------------------- | ----------------------------------------------------------------------------------------------------------------------------------------------------------- | --------------------------------------------------- | --------------- | ---------------------------------------------------------------------------------------- | ---------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------- | ---------------------- | ------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------- | -------------------------------------------------------------------- | ----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------- | ------------------ | ----------------------------------------------------------------------------------------------------------------- | ------------------------ | -------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------- | -------------------- | -------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------- | ------------- | ----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------- | ----------------- | -------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------- | ---------------------------- | ------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------ | ------------ | -------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------- | ----------- | ---------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------- | ---------- | ------------ | --------- | -------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------- | ------- | -- | ------- | ---------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------- |
|
The infinite series ∑ = 1 - 1 + 1 - 1 + 1 - 1 + … , called Grandi's series, also written: ∞ ∑ (-1)n n_=0 is a divergent series, meaning that it lacks a sum in the usual sense... In fact, if you treat this series like a telescoping series and/or use different bracketing procedures to sum it, you may obtain contradictory results... ∑ = 1 - 1 + 1 - 1 + 1 - 1 + 1 - 1 + ... = ∑1 = (1-1) + (1-1) + (1-1) + (1-1) + ... = 0 ∑2 = 1 + (-1+1) + (-1+1) + (-1+1) + ... = 1 ∑3 = 1 + (1-1+1-1+1-1+ ...) = 1 + ∑ => ∑ = 1/2 As shown above, it appears to equal 0 and 1, yet in some sense 'sums' to 1/2, producing a paradox... The error here is that the associative law cannot be applied freely to an infinite sum unless the sum is absolutely convergent. We can say that the sum of Grandi's series is NaN. | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | |
| ----------------------------------------------------------------------------------------------------------------------------------------------------------- | ----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------- | ------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------- | ------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------- | -------------------------------------------------------------------------------------------------------------------------------------------------------------- | --------------------------------------------------------------------------------------------- | ----------------------------------------------------------------------------------------------------------------------------------------------------------- | --------------------------------------------------- | --------------- | ---------------------------------------------------------------------------------------- | ---------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------- | ---------------------- | ------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------- | -------------------------------------------------------------------- | ----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------- | ------------------ | ----------------------------------------------------------------------------------------------------------------- | ------------------------ | -------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------- | -------------------- | -------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------- | ------------- | ----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------- | ----------------- | -------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------- | ---------------------------- | ------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------ | ------------ | -------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------- | ----------- | ---------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------- | ---------- | ------------ | --------- | -------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------- | ------- | -- | ------- | ---------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------- |
|  | = i, is the imaginary unit of any imaginary number. Discovered by the Italian mathematician Girolamo Cardano. An imaginary number is a number of the form **b_i** where 'b' is a real number, 'i' is the square root of -1, for b
| = i, is the imaginary unit of any imaginary number. Discovered by the Italian mathematician Girolamo Cardano. An imaginary number is a number of the form **b_i** where 'b' is a real number, 'i' is the square root of -1, for b  0. Imaginary numbers (and complex numbers in general) are essential for describing physical reality and have concrete applications in: electromagnetism, signal processing, control theory, quantum mechanics, cryptology, and cartography... is the result of the folowing equations: x2 + 1 = 0 (for x
0. Imaginary numbers (and complex numbers in general) are essential for describing physical reality and have concrete applications in: electromagnetism, signal processing, control theory, quantum mechanics, cryptology, and cartography... is the result of the folowing equations: x2 + 1 = 0 (for x  -i) Square roots of negative numbers other than -1 can be written under the form:
-i) Square roots of negative numbers other than -1 can be written under the form:  -n = i
-n = i n e_i
n e_i /2 = cos (
/2 = cos ( /2) + i sin (
/2) + i sin ( /2) = i i to the i is a real number ii = e-
/2) = i i to the i is a real number ii = e- /2 ≈ 0.207879576... (cf. i to the i is a Real Number) Proof From Euler's formula: e_ix_ = cos(x) + i sin(x) Then e_i_
/2 ≈ 0.207879576... (cf. i to the i is a Real Number) Proof From Euler's formula: e_ix_ = cos(x) + i sin(x) Then e_i_ /2 = cos(
/2 = cos( /2) + i sin(
/2) + i sin( /2) = i Raising both sides to i_-th power: e_i·i
/2) = i Raising both sides to i_-th power: e_i·i /2 = e-
/2 = e- /2 = ii, which is approximately 0.207879576... (Actually, this is one of many possible values for i to the i) The reciprocal of i is -i: i_-1 = 1/i = i/i_2 = i/-1 = -i Powers of i repeat in a definite pattern (i, -1, -i, 1, ...): i_1 = i i_2 = -1 i_3 = i_2_i = (-1)i = -i i_4 = i_3_i = (-i)i = -(i_2) = -(-1) = 1 i_5 = i_4_i = (1)i = i ... Multiplicative table with i 1 -1 i -i 1 1 -1 i -i -1 -1 1 -i i i i -i -1 1 -i -i i 1 -1 The first roots of i are: 1
/2 = ii, which is approximately 0.207879576... (Actually, this is one of many possible values for i to the i) The reciprocal of i is -i: i_-1 = 1/i = i/i_2 = i/-1 = -i Powers of i repeat in a definite pattern (i, -1, -i, 1, ...): i_1 = i i_2 = -1 i_3 = i_2_i = (-1)i = -i i_4 = i_3_i = (-i)i = -(i_2) = -(-1) = 1 i_5 = i_4_i = (1)i = i ... Multiplicative table with i 1 -1 i -i 1 1 -1 i -i -1 -1 1 -i i i i -i -1 1 -i -i i 1 -1 The first roots of i are: 1 i = i 2
i = i 2 i = ±(1 + i)/
i = ±(1 + i)/ 2 3
2 3 i = (
i = ( 3 + i)/2 4
3 + i)/2 4 i = ±(i
i = ±(i (2 -
(2 -  2) +
2) +  (2 +
(2 +  2))/2 5
2))/2 5 i = i A 'paradox' (or a math fallacy?) with i: a)
i = i A 'paradox' (or a math fallacy?) with i: a)  -1 =
-1 =  -1 b)
-1 b)  (1/-1) =
(1/-1) =  (-1/1) c)
(-1/1) c)  1/
1/ -1 =
-1 =  -1/
-1/ 1 d) (
1 d) ( 1)2 = (
1)2 = ( -1)2 e) 1 = -1 and then 2 = 0 ??? Is this possible? Can you discover what led to this poetic licenced conclusion? A strange right triangle involving i:
-1)2 e) 1 = -1 and then 2 = 0 ??? Is this possible? Can you discover what led to this poetic licenced conclusion? A strange right triangle involving i:  | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | |
| -1 | is the first and largest negative integer. is a Heegner number. In number theory, "Wilson's theorem" states that a natural number greater than 1 is a prime number if and only if: (n - 1)! == -1(mod n) Multiplying any number by -1 is equivalent to changing the sign on the number. Curiously enough, one of the values of (−1)2.2 is −1 x-1 = 1/x 1/(-1) = (-1)/1 = ei
| | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | |
| -1 | is the first and largest negative integer. is a Heegner number. In number theory, "Wilson's theorem" states that a natural number greater than 1 is a prime number if and only if: (n - 1)! == -1(mod n) Multiplying any number by -1 is equivalent to changing the sign on the number. Curiously enough, one of the values of (−1)2.2 is −1 x-1 = 1/x 1/(-1) = (-1)/1 = ei ≈ sin2017(2)1/5 | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | |
| 0 ⠼⠚
≈ sin2017(2)1/5 | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | |
| 0 ⠼⠚  |
|  Ancient civilizations like the Greeks and Romans didn’t use zero in their numeral systems. It wasn’t until Indian mathematician Brahmagupta introduced it around the 7th century CE that zero gained recognition as a number with its own value and function. is a separate and special entity called 'Identity element'. 0 is actually the identity element under addition for the real numbers, since if a is any real number, a + 0 = 0 + a = a. Mathematicians refers to 0 as the additive identity (or better said, the reflexive identity of addition). is considered to be a purely imaginary number: 0 is the only complex number which is both real and purely imaginary. identifies the concept of "almost" impossible in probability. More generally, the concept of almost nowhere in measure theory. 0 = n / ∞ (according to IEEE 754) 0 = log_a_1 a0 = 1, only when a doesn't equal 0. By convention, you cannot divide any number by zero. In theory, zero multiplied by infinity is undetermined (as is zero divided by zero). It is the only integer (actually, the only real number) that is neither negative nor positive. The question whether 'zero' is odd or even seems to be totally subjective. But technically, 0 should be considered an even number. All even numbers can be expressed in the algebraic form 2_n, where n is any integer, positive, negative or zero. Thus 0 = 2 x 0, 2 = 2 x 1, 4 = 2 x 2, and so on. All odd numbers can be expressed in the form 2_n+1, thus 1 = (2 x 0) + 1, 3 = (2 x 1) + 1, 5 = (2 x 2) + 1, etc. Zero cannot be odd, since there is no whole number n such that 2_n+1 = 0. Mathematical equations with one or more unknown factors are solved by equalizing them to zero. is the number of n x n magic squares for n = 2. Remarkably, a string of eight zeroes (00000000 !) emerges at position 172,330,850 in the decimal representation of π, counting from the digit immediately following the decimal point. Below is the string, along with the digits surrounding it:
Ancient civilizations like the Greeks and Romans didn’t use zero in their numeral systems. It wasn’t until Indian mathematician Brahmagupta introduced it around the 7th century CE that zero gained recognition as a number with its own value and function. is a separate and special entity called 'Identity element'. 0 is actually the identity element under addition for the real numbers, since if a is any real number, a + 0 = 0 + a = a. Mathematicians refers to 0 as the additive identity (or better said, the reflexive identity of addition). is considered to be a purely imaginary number: 0 is the only complex number which is both real and purely imaginary. identifies the concept of "almost" impossible in probability. More generally, the concept of almost nowhere in measure theory. 0 = n / ∞ (according to IEEE 754) 0 = log_a_1 a0 = 1, only when a doesn't equal 0. By convention, you cannot divide any number by zero. In theory, zero multiplied by infinity is undetermined (as is zero divided by zero). It is the only integer (actually, the only real number) that is neither negative nor positive. The question whether 'zero' is odd or even seems to be totally subjective. But technically, 0 should be considered an even number. All even numbers can be expressed in the algebraic form 2_n, where n is any integer, positive, negative or zero. Thus 0 = 2 x 0, 2 = 2 x 1, 4 = 2 x 2, and so on. All odd numbers can be expressed in the form 2_n+1, thus 1 = (2 x 0) + 1, 3 = (2 x 1) + 1, 5 = (2 x 2) + 1, etc. Zero cannot be odd, since there is no whole number n such that 2_n+1 = 0. Mathematical equations with one or more unknown factors are solved by equalizing them to zero. is the number of n x n magic squares for n = 2. Remarkably, a string of eight zeroes (00000000 !) emerges at position 172,330,850 in the decimal representation of π, counting from the digit immediately following the decimal point. Below is the string, along with the digits surrounding it:  The difference between 3, 30, and 300 may seem like just a few extra zeros, but those little circles are actually one of the world's greatest inventions. Around 200 B.C., Hindu scholars started using nine oddly shaped symbols and a dot to bring order to the world of math. These symbols and the dot were the earliest predecessors of our modern numbers 0, 1, 2, 3, 4, 5, 6, 7, 8, and 9. With only ten symbols and a base of ten, the Hindu numeral system was simple to learn and use. It's unknown who first thought of using a dot (bindu in Sanskrit) as the tenth number. However, it's possible that a Hindu, using an abacus, wanted to keep a written record of his calculations. One day, he used a symbol '.' called shunya to represent a column on his counting board where no beads were moved... Originally, shunya (
The difference between 3, 30, and 300 may seem like just a few extra zeros, but those little circles are actually one of the world's greatest inventions. Around 200 B.C., Hindu scholars started using nine oddly shaped symbols and a dot to bring order to the world of math. These symbols and the dot were the earliest predecessors of our modern numbers 0, 1, 2, 3, 4, 5, 6, 7, 8, and 9. With only ten symbols and a base of ten, the Hindu numeral system was simple to learn and use. It's unknown who first thought of using a dot (bindu in Sanskrit) as the tenth number. However, it's possible that a Hindu, using an abacus, wanted to keep a written record of his calculations. One day, he used a symbol '.' called shunya to represent a column on his counting board where no beads were moved... Originally, shunya ( ), the dot, was not the number zero itself, but simply a mark indicating empty space. The origin of the word "zero" can be traced back to the Italian mathematician Leonardo Pisano, also known as Fibonacci. He took the Arabic word 'صِفْر' (sifr, from the semitic root s.p.r.), meaning 'empty', and transformed it into the Italian word zefiro, which later evolved into "zero." This term has been adopted by many languages such as English, Catalan, French (zéro), Portuguese, Romanian, Spanish (cero), Wallon (zérô), Albanian, Polish, and Japanese. Europe is divided into two regions: the 'zero region' (mentioned earlier) and the 'nullus region' (derived from the Latin word for 'zero', nullus). The 'nullus region' includes Germanic, Scandinavian, and some Slavic countries. Below is a table showcasing the word for 0 in a selection of languages from the 'nullus region': Dutch nul Czech nula German null Russian nol' Swedish noll Slovak nula The Greek word for zero is μηδεν, read as 'meden', which means, etymologically, not even one (i.e. nothing). The Oracle of Delphi in ancient Greece had a wise motto, like this: "meden agan" - nothing too much (or nothing in excess)... - posted by George Pantazis
), the dot, was not the number zero itself, but simply a mark indicating empty space. The origin of the word "zero" can be traced back to the Italian mathematician Leonardo Pisano, also known as Fibonacci. He took the Arabic word 'صِفْر' (sifr, from the semitic root s.p.r.), meaning 'empty', and transformed it into the Italian word zefiro, which later evolved into "zero." This term has been adopted by many languages such as English, Catalan, French (zéro), Portuguese, Romanian, Spanish (cero), Wallon (zérô), Albanian, Polish, and Japanese. Europe is divided into two regions: the 'zero region' (mentioned earlier) and the 'nullus region' (derived from the Latin word for 'zero', nullus). The 'nullus region' includes Germanic, Scandinavian, and some Slavic countries. Below is a table showcasing the word for 0 in a selection of languages from the 'nullus region': Dutch nul Czech nula German null Russian nol' Swedish noll Slovak nula The Greek word for zero is μηδεν, read as 'meden', which means, etymologically, not even one (i.e. nothing). The Oracle of Delphi in ancient Greece had a wise motto, like this: "meden agan" - nothing too much (or nothing in excess)... - posted by George Pantazis  The Chinese character for 0, 零, combines 雨 (yǔ) meaning "rain" and 令 (lìng) meaning "to order." This fusion originally represented a fine mist and symbolized the 'last part.' Picture it as an enveloping mist where nothing (zero) is visible or as the round shape of a raindrop. Love is a score of 0 in tennis. What English word contains 0 vowels? Answer: hymn, gypsyfy, myth, rhythm, sylph, syzygy, etc. The Czech phrase: Strc prst skrz krk meaning "thrust finger through neck", contains 0 vowels and semi-vowels! In German, the expression in Null Komma nichts (in zero point nothing) means 'in a trice' In Italian, the expression a chilometri zero (in zero kilometers from any location) means 'local'. For instance, un gelato a chilometri zero translates as 'an ice-cream produced with local products'. There are no letters assigned to the numbers 0 and 1 on a phone dial. These numbers remain unassigned because they are so-called 'flag' numbers, kept for special purposes such as emergency or operator services. "Wuji" (Number 0), in the Mystical Numbers of Taoism, represents the Null, the Chaos, the Origin and the End. Joke: Chuck Norris can divide by zero. (More Chuck Norris facts) Zero Star Hotel (Null Stern Hotel) The "Null Stern", or "Zero Star" Hotel is a cross between a hostel and an art installation by Swiss concept artists Frank and Patrik Riklin. This hotel is actually a converted bomb shelter...
The Chinese character for 0, 零, combines 雨 (yǔ) meaning "rain" and 令 (lìng) meaning "to order." This fusion originally represented a fine mist and symbolized the 'last part.' Picture it as an enveloping mist where nothing (zero) is visible or as the round shape of a raindrop. Love is a score of 0 in tennis. What English word contains 0 vowels? Answer: hymn, gypsyfy, myth, rhythm, sylph, syzygy, etc. The Czech phrase: Strc prst skrz krk meaning "thrust finger through neck", contains 0 vowels and semi-vowels! In German, the expression in Null Komma nichts (in zero point nothing) means 'in a trice' In Italian, the expression a chilometri zero (in zero kilometers from any location) means 'local'. For instance, un gelato a chilometri zero translates as 'an ice-cream produced with local products'. There are no letters assigned to the numbers 0 and 1 on a phone dial. These numbers remain unassigned because they are so-called 'flag' numbers, kept for special purposes such as emergency or operator services. "Wuji" (Number 0), in the Mystical Numbers of Taoism, represents the Null, the Chaos, the Origin and the End. Joke: Chuck Norris can divide by zero. (More Chuck Norris facts) Zero Star Hotel (Null Stern Hotel) The "Null Stern", or "Zero Star" Hotel is a cross between a hostel and an art installation by Swiss concept artists Frank and Patrik Riklin. This hotel is actually a converted bomb shelter...  | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | |
| 1/2 | = sinus(30°) = cosinus(60°) = cosinus(30°)/
| | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | |
| 1/2 | = sinus(30°) = cosinus(60°) = cosinus(30°)/ 3 = 1/3 + 1/6 A strange factorial: (1/2)! = (√π)/2 Using all digits from 1 to 9 once: = 6 729 / 13 458 = 9 327 / 18 654 (there are 10 other possibilities to write similar fractions by using all digits from 1 to 9 once) = (123 - 45) / (67 + 89) Using the same number twice, but just swapping the place of ONE digit: = 105263157894736842 / 210526315789473684 = 157894736842105263 / 315789473684210526 = 210526315789473684 / 421052631578947368 = 263157894736842105 / 526315789473684210 = 315789473684210526 / 631578947368421052 = 368421052631578947 / 736842105263157894 = 421052631578947368 / 842105263157894736 = 473684210526315789 / 947368421052631578 Numbers with such properties are called 'parasit or parasitic numbers'. ≈ angular magnitude of the Sun, and of the Moon. In a group of 23 people, at least two have the same birthday with the probability greater than 1/2. Another 'paradox' (or math fallacy?) involving 1/2: Since (1/2)2 = 1/4 and (1/2)3 = 1/8 then (1/2)3 < (1/2)2 using the logarithms we obtain: 3 log (1/2) < 2 log (1/2) and after dividing by log (1/2): **3** < **2** How can that be? The population of the Roman Empire under Augustus was about one hundred millions, of which more than **one half** were slaves! **There is a 1/2 percent probability you are related to Genghis Khan...** An international group of geneticists studying Y-chromosome data have found that nearly 8 percent of the men living in the region of the former Mongol empire carry y-chromosomes that are nearly identical to those of Genghis Khan, the fearsome Mongolian warrior of the 13th century, whose adopted name means "Universal Ruler" in Altaic, his native tongue. That translates to 0.5 percent of the global population in the world (or roughly 16 million descendants living today). Did you know that the Romans too could transcribe unit fractions? e.g. to write **1/2** they used the letter **S** (semis). Knowing that, what represents the Roman numeral SIX? Obviously not 6, but 8.5! (10 - 1 - 1/2) In Italy, "fojetta" (_small leaf_, in Roman dialect) is a measure corresponding to half a liter of wine. A typical 'fojetta' ->
3 = 1/3 + 1/6 A strange factorial: (1/2)! = (√π)/2 Using all digits from 1 to 9 once: = 6 729 / 13 458 = 9 327 / 18 654 (there are 10 other possibilities to write similar fractions by using all digits from 1 to 9 once) = (123 - 45) / (67 + 89) Using the same number twice, but just swapping the place of ONE digit: = 105263157894736842 / 210526315789473684 = 157894736842105263 / 315789473684210526 = 210526315789473684 / 421052631578947368 = 263157894736842105 / 526315789473684210 = 315789473684210526 / 631578947368421052 = 368421052631578947 / 736842105263157894 = 421052631578947368 / 842105263157894736 = 473684210526315789 / 947368421052631578 Numbers with such properties are called 'parasit or parasitic numbers'. ≈ angular magnitude of the Sun, and of the Moon. In a group of 23 people, at least two have the same birthday with the probability greater than 1/2. Another 'paradox' (or math fallacy?) involving 1/2: Since (1/2)2 = 1/4 and (1/2)3 = 1/8 then (1/2)3 < (1/2)2 using the logarithms we obtain: 3 log (1/2) < 2 log (1/2) and after dividing by log (1/2): **3** < **2** How can that be? The population of the Roman Empire under Augustus was about one hundred millions, of which more than **one half** were slaves! **There is a 1/2 percent probability you are related to Genghis Khan...** An international group of geneticists studying Y-chromosome data have found that nearly 8 percent of the men living in the region of the former Mongol empire carry y-chromosomes that are nearly identical to those of Genghis Khan, the fearsome Mongolian warrior of the 13th century, whose adopted name means "Universal Ruler" in Altaic, his native tongue. That translates to 0.5 percent of the global population in the world (or roughly 16 million descendants living today). Did you know that the Romans too could transcribe unit fractions? e.g. to write **1/2** they used the letter **S** (semis). Knowing that, what represents the Roman numeral SIX? Obviously not 6, but 8.5! (10 - 1 - 1/2) In Italy, "fojetta" (_small leaf_, in Roman dialect) is a measure corresponding to half a liter of wine. A typical 'fojetta' ->  Tupper's self-referential formula is an amazing formula concocted by Jeff Tupper that, when graphed in 2 dimensions, can visually reproduce the formula itself:
Tupper's self-referential formula is an amazing formula concocted by Jeff Tupper that, when graphed in 2 dimensions, can visually reproduce the formula itself:  If one graphs the set of points (x, y) with 0 < _x_ < 106 and _k_ < _y_ < (_k_ + 17), such that they satisfy the inequality given above, the resulting self-referential 'plot' looks like this:
If one graphs the set of points (x, y) with 0 < _x_ < 106 and _k_ < _y_ < (_k_ + 17), such that they satisfy the inequality given above, the resulting self-referential 'plot' looks like this:  | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | |
| **1 ⠼⠁** I **
| | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | |
| **1 ⠼⠁** I **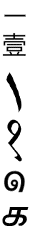 ** | is a separate and special entity called 'Unity' or 'Identity element'. 1 is actually the identity element under multiplication for the real numbers, since _a_ x 1 = 1 x _a_ = _a_. Mathematicians refers to 1 as the _multiplicative identity_ (or better said, the _reflexive identity of multiplication_). is NOT prime! Primes or prime numbers can be poetically described as the 'atoms' of mathematics - the building blocks of the world of numbers. But, mathematically speaking: "_a prime number is a positive integer with exactly TWO positive divisors: 1 and itself_". Modern textbooks consider 1 neither prime nor composite, whereas older texts generally asserted the contrary. In 1859, Henri Lebesgue stated explicitly that 1 is prime in "Exercices d'analyse numérique". It is also prime in "Primary Elements of Algebra for Common Schools and Academies" (1866) by Joseph Ray, and in "Standard Arithmetic" (1892) by William J. Milne. A list of primes to 10,006,721 published in 1914 by Derrick N. Lehmer includes 1 ("List of prime numbers from 1 to 10,006,721", Carnegie Institution of Washington). is the solution of the equation: x3 - x = 0 (for x
** | is a separate and special entity called 'Unity' or 'Identity element'. 1 is actually the identity element under multiplication for the real numbers, since _a_ x 1 = 1 x _a_ = _a_. Mathematicians refers to 1 as the _multiplicative identity_ (or better said, the _reflexive identity of multiplication_). is NOT prime! Primes or prime numbers can be poetically described as the 'atoms' of mathematics - the building blocks of the world of numbers. But, mathematically speaking: "_a prime number is a positive integer with exactly TWO positive divisors: 1 and itself_". Modern textbooks consider 1 neither prime nor composite, whereas older texts generally asserted the contrary. In 1859, Henri Lebesgue stated explicitly that 1 is prime in "Exercices d'analyse numérique". It is also prime in "Primary Elements of Algebra for Common Schools and Academies" (1866) by Joseph Ray, and in "Standard Arithmetic" (1892) by William J. Milne. A list of primes to 10,006,721 published in 1914 by Derrick N. Lehmer includes 1 ("List of prime numbers from 1 to 10,006,721", Carnegie Institution of Washington). is the solution of the equation: x3 - x = 0 (for x  -1, or 0) [Note: x3 - x can be factorized as follows: x(x + 1)(x - 1)] is the only real solution of the equation x3 + 3x - 4 = 0 Benford's law states that in a huge assortment of number sequences - in listings, tables of statistics, random samples from a day's stock quotations, a tournament's tennis scores, the populations of towns, electricity bills in the Solomon Islands, and much more, **the digit 1 tends to occur with probability ∼30%**, much greater than the expected 11.1% (i.e., one digit out of 9). Dr. Nigrini gained recognition by applying a system he devised based on Benford's Law to some fraud cases in Brooklyn. The idea underlying his system is that if the numbers in a set of data like a tax return more or less match the frequencies and ratios predicted by Benford's Law, the data are probably honest. But if a graph of such numbers is markedly different from the one predicted by Benford's Law, he said, "I think I'd call someone in for a detailed audit". Mathematicians define a 'sphere' as the surface of a sphere, not a solid ball, so a sphere has 2 sides: the outside and the inside. However, there are also 1-sided surfaces! _f_(x) = _e_x at the point x = 0 is exactly 1. =0! Why 0! = 1? Because 4! = 4x3x2x1 and 3! = 3x2x1. Therefore 4! = 4x3! In the same way 3! = 3x2! and 2! = 2x1! So it follows that 1! = 1x0! Therefore 0! must be equal to 1 or 1! would be 0... And so 2! would be zero and then 3! and so on. Simple math relations: x**1** = x and **1**x = 1 = log_a_ _a_ = log_b_ _a_ / log_a_ _b_ = _a_0 (for _a_
-1, or 0) [Note: x3 - x can be factorized as follows: x(x + 1)(x - 1)] is the only real solution of the equation x3 + 3x - 4 = 0 Benford's law states that in a huge assortment of number sequences - in listings, tables of statistics, random samples from a day's stock quotations, a tournament's tennis scores, the populations of towns, electricity bills in the Solomon Islands, and much more, **the digit 1 tends to occur with probability ∼30%**, much greater than the expected 11.1% (i.e., one digit out of 9). Dr. Nigrini gained recognition by applying a system he devised based on Benford's Law to some fraud cases in Brooklyn. The idea underlying his system is that if the numbers in a set of data like a tax return more or less match the frequencies and ratios predicted by Benford's Law, the data are probably honest. But if a graph of such numbers is markedly different from the one predicted by Benford's Law, he said, "I think I'd call someone in for a detailed audit". Mathematicians define a 'sphere' as the surface of a sphere, not a solid ball, so a sphere has 2 sides: the outside and the inside. However, there are also 1-sided surfaces! _f_(x) = _e_x at the point x = 0 is exactly 1. =0! Why 0! = 1? Because 4! = 4x3x2x1 and 3! = 3x2x1. Therefore 4! = 4x3! In the same way 3! = 3x2! and 2! = 2x1! So it follows that 1! = 1x0! Therefore 0! must be equal to 1 or 1! would be 0... And so 2! would be zero and then 3! and so on. Simple math relations: x**1** = x and **1**x = 1 = log_a_ _a_ = log_b_ _a_ / log_a_ _b_ = _a_0 (for _a_ 0) = _a_2 - (_a_ + 1)(_a_ - 1) = 35 - 32 - 52 = 75 - 72 - 52 = 1/2 + 1/3 + 1/6 = 1/2 + 1/4 + 1/6 + 1/12 = 1/21 + 1/22 + 1/23 + 1/24 + 1/25 + ... = (2 + _
0) = _a_2 - (_a_ + 1)(_a_ - 1) = 35 - 32 - 52 = 75 - 72 - 52 = 1/2 + 1/3 + 1/6 = 1/2 + 1/4 + 1/6 + 1/12 = 1/21 + 1/22 + 1/23 + 1/24 + 1/25 + ... = (2 + _ _5)1/3 + (2 - _
_5)1/3 + (2 - _ _5)1/3 = (1 + **_i_**)(1 - **_i_**)/2 = sin2 (a) + cos2 (a) = | F_n_ x F_n_+3 - F_n_+1 x F_n_+2 | (F = Fibonacci numbers) = 1/(1x2) + 1/(2x3) + 1/(3x4) + 1/(4x5) + ... + 1/n(n+1) = 0.9 = 0.9 + 0.09 + 0.009 + 0.0009 + 0.00009 + ...
_5)1/3 = (1 + **_i_**)(1 - **_i_**)/2 = sin2 (a) + cos2 (a) = | F_n_ x F_n_+3 - F_n_+1 x F_n_+2 | (F = Fibonacci numbers) = 1/(1x2) + 1/(2x3) + 1/(3x4) + 1/(4x5) + ... + 1/n(n+1) = 0.9 = 0.9 + 0.09 + 0.009 + 0.0009 + 0.00009 + ... 
 _n_ = 1
_n_ = 1  (1 + 2 + 3 + ... + _n_)1/_n_ = 1
(1 + 2 + 3 + ... + _n_)1/_n_ = 1  (_sin_ x)/x = 1
(_sin_ x)/x = 1  (_e_x - 1)/x = 1
(_e_x - 1)/x = 1  ln(1 + x)/x = 1 a_p_-1 ≡ 1 (mod _p_) [_p_ = prime number] = e2_**i**_
ln(1 + x)/x = 1 a_p_-1 ≡ 1 (mod _p_) [_p_ = prime number] = e2_**i**_ = 35/70 + 148/296 (all digits 0 through 9 were used once!) = 3
= 35/70 + 148/296 (all digits 0 through 9 were used once!) = 3 (13
(13 3/36 **+** 5/8) - 3
3/36 **+** 5/8) - 3 (13
(13 3/36 **-** 5/8) Curious multiplications using 1's: 1 x 1 = 1 11 x 11 = 121 111 x 111 = 12321 1111 x 1111 = 1234321 11111 x 11111 = 123454321 etc... The numbers in the series **1**, **11**, **111**, **1111**, **11111**, etc... are all triangular numbers in **base-9**. During any police lineup the suspects wear nos. 2 through 9 because it is considered too suggestive to make anyone display the no. **1**! Symbolizes the essence of all phenomena, which is a single unity, before being divided. It represents also the contrast between essence and existence; the enduring and the ephemeral; the unity in diversity (one/many). According to Hopper, the first advance towards counting is with the use of words for _one_ and for _many_, the differentiation from the self from the group. We still say 'numero uno' to speak of ourselves. "Taiji" (also termed as "Dayi" or "Taiyi"), in the Mystical Numbers of Taoism, represents the ONE, the Ultimate, the Order. The martial art known as "Taijiquan" based its movement's philosophies upon the notion of Taiji. In the English language, there is a word with just ONE vowel which occurs 6 times: indivisibility. 'Strengths' is the longest word in the English language with just ONE vowel. **Impoverished counting system: 1 + 1 = ?** When it comes to counting, a remote Amazonian tribespeople have been found to be lost for words. In fact, researchers discovered that Pirahã tribe of Brazil, with a population of 200, have no words beyond ONE, two and many. The word for "one" can also mean "a few", while "two" can also be used to refer to "not many"... (But is there any case where not having words for something doesn't allow you to think about it?) _Source BBC_ **ONE** in different languages (© G. Sarcone) (Old English _**ān**_) Reconstructed proto-language: | * **TIK** | Indo-european | * **OIN**-, * **OIW**-, * **OIK**- | , | * **SEM**- | Sanskrit | **
3/36 **-** 5/8) Curious multiplications using 1's: 1 x 1 = 1 11 x 11 = 121 111 x 111 = 12321 1111 x 1111 = 1234321 11111 x 11111 = 123454321 etc... The numbers in the series **1**, **11**, **111**, **1111**, **11111**, etc... are all triangular numbers in **base-9**. During any police lineup the suspects wear nos. 2 through 9 because it is considered too suggestive to make anyone display the no. **1**! Symbolizes the essence of all phenomena, which is a single unity, before being divided. It represents also the contrast between essence and existence; the enduring and the ephemeral; the unity in diversity (one/many). According to Hopper, the first advance towards counting is with the use of words for _one_ and for _many_, the differentiation from the self from the group. We still say 'numero uno' to speak of ourselves. "Taiji" (also termed as "Dayi" or "Taiyi"), in the Mystical Numbers of Taoism, represents the ONE, the Ultimate, the Order. The martial art known as "Taijiquan" based its movement's philosophies upon the notion of Taiji. In the English language, there is a word with just ONE vowel which occurs 6 times: indivisibility. 'Strengths' is the longest word in the English language with just ONE vowel. **Impoverished counting system: 1 + 1 = ?** When it comes to counting, a remote Amazonian tribespeople have been found to be lost for words. In fact, researchers discovered that Pirahã tribe of Brazil, with a population of 200, have no words beyond ONE, two and many. The word for "one" can also mean "a few", while "two" can also be used to refer to "not many"... (But is there any case where not having words for something doesn't allow you to think about it?) _Source BBC_ **ONE** in different languages (© G. Sarcone) (Old English _**ān**_) Reconstructed proto-language: | * **TIK** | Indo-european | * **OIN**-, * **OIW**-, * **OIK**- | , | * **SEM**- | Sanskrit | ** _EKA_** |
_EKA_** |  _**ekaḥ**_ (m) / _**ekā**_ (f) / _**ekam**_ (n) Proto-Hellenic | * **HEMS** (< _sems_) | Greek, Attic | **'EIΣ**, **MIA**, **'EN _HÊS_** (m), **_MIA_** (f), **_HÉN_** (n) | Latin | **VNVS**, -**A** | Archaic Latin | * **ŒNVS**, -**A** | , | * **OINOS**, -**A** | Italian, Spanish _**uno**_; Romanian, French, and Catalan _**un**_; Provençal _**uns**_; Portuguese _**um**_; Romansh _**in**_; Sardinian _**únu**_. Old Celtic | **OINO** | Breton _**unan**_; Welsh **_un_**; Irish **_a haon_** (cardinal), **_amháin_** (thing), **_duine_** (person). Old Germanic | **AINAZ** | Dutch _**een**_; German _**eins**_; Danish and Norwegian _**en**_, _**et**_; Swedish **_ett_**; Icelandic **_einn_**. Old Slavic | **JEDINU**, **-A**, **-0** | Russian один _**odin**_; Czech and Polish _**jeden**_; Slovenian **_êna_**. Proto Indo-Iranian | * **AIWAS** | Persian یک **_yek_**; Hindi एक **_ek_**.
_**ekaḥ**_ (m) / _**ekā**_ (f) / _**ekam**_ (n) Proto-Hellenic | * **HEMS** (< _sems_) | Greek, Attic | **'EIΣ**, **MIA**, **'EN _HÊS_** (m), **_MIA_** (f), **_HÉN_** (n) | Latin | **VNVS**, -**A** | Archaic Latin | * **ŒNVS**, -**A** | , | * **OINOS**, -**A** | Italian, Spanish _**uno**_; Romanian, French, and Catalan _**un**_; Provençal _**uns**_; Portuguese _**um**_; Romansh _**in**_; Sardinian _**únu**_. Old Celtic | **OINO** | Breton _**unan**_; Welsh **_un_**; Irish **_a haon_** (cardinal), **_amháin_** (thing), **_duine_** (person). Old Germanic | **AINAZ** | Dutch _**een**_; German _**eins**_; Danish and Norwegian _**en**_, _**et**_; Swedish **_ett_**; Icelandic **_einn_**. Old Slavic | **JEDINU**, **-A**, **-0** | Russian один _**odin**_; Czech and Polish _**jeden**_; Slovenian **_êna_**. Proto Indo-Iranian | * **AIWAS** | Persian یک **_yek_**; Hindi एक **_ek_**.  Evolution from 'seal script' to modern sinograph 一 : Old Chinese (pron.) | **iêt** | Chinese 一 _**yī**_. 幺 _**yāo**_ is used as a replacement for _yī_ in series of digits such as phone numbers, room numbers, etc... to prevent confusion between similar sounding words. Proto-Semitic | * **HAD** | ; | **'IShT** | Semitic root | **WHD** | or | **?HD** | (**?** = glotal stop) Ancient Egyptian [w'.-] _**ua-**_; Akkadian _
Evolution from 'seal script' to modern sinograph 一 : Old Chinese (pron.) | **iêt** | Chinese 一 _**yī**_. 幺 _**yāo**_ is used as a replacement for _yī_ in series of digits such as phone numbers, room numbers, etc... to prevent confusion between similar sounding words. Proto-Semitic | * **HAD** | ; | **'IShT** | Semitic root | **WHD** | or | **?HD** | (**?** = glotal stop) Ancient Egyptian [w'.-] _**ua-**_; Akkadian _ **ishte'n**_; Punic _
**ishte'n**_; Punic _ _ _**e'hd**_ Arabic واحِد _**wa:hid**_; Hebrew אחת **_'aHat_**; Maltese: _**wiehed**_; Amharic _**and**_. More languagesMagyar _**egy**_. Turkish _**bir**_. Mayan **_hun_**. Nahuatl _**cē**_. Suomi **_yksi_**. Zulu **_(u-ku)nye_**. HIDDEN ROOTSThe roots of the word **one** (un-, sim-, prin-, cen-) are hidden in the following words: inch (from Lat. _uncia_), onion, ounce, primal, primate, primitive, primrose, prince, recent, simple, simulate, sincere (from Lat. _sincerus_ meaning "clean, pure, sound", derived from the Indo-European roots ‘_sem_’ and ‘_ker_’, the underlying meaning of which is: 'of one growth', hence 'pure, clean'), single, unanimous, unicorn, uniform, unify, union, unique, unit, universe; alone, any, lonely, only, none. In French: ensemble, oignon, premier, printemps, sanglier, semblable, sincère. In Spanish: centolla, centollo ('spider-crab', from Celtic *_kintuollos_, the largest one < *_kĭntu_-, first, and *_ollos_, big). Gaulish person names: Cintullus, Cintugnatos, 'first born' (< *_kĭntu_-, first one; cognates: Lat. _re-cens_ 'new', Gr. _kainos_ 'young, new'). |
|
_ _**e'hd**_ Arabic واحِد _**wa:hid**_; Hebrew אחת **_'aHat_**; Maltese: _**wiehed**_; Amharic _**and**_. More languagesMagyar _**egy**_. Turkish _**bir**_. Mayan **_hun_**. Nahuatl _**cē**_. Suomi **_yksi_**. Zulu **_(u-ku)nye_**. HIDDEN ROOTSThe roots of the word **one** (un-, sim-, prin-, cen-) are hidden in the following words: inch (from Lat. _uncia_), onion, ounce, primal, primate, primitive, primrose, prince, recent, simple, simulate, sincere (from Lat. _sincerus_ meaning "clean, pure, sound", derived from the Indo-European roots ‘_sem_’ and ‘_ker_’, the underlying meaning of which is: 'of one growth', hence 'pure, clean'), single, unanimous, unicorn, uniform, unify, union, unique, unit, universe; alone, any, lonely, only, none. In French: ensemble, oignon, premier, printemps, sanglier, semblable, sincère. In Spanish: centolla, centollo ('spider-crab', from Celtic *_kintuollos_, the largest one < *_kĭntu_-, first, and *_ollos_, big). Gaulish person names: Cintullus, Cintugnatos, 'first born' (< *_kĭntu_-, first one; cognates: Lat. _re-cens_ 'new', Gr. _kainos_ 'young, new'). |
|  **1.41** | is also called _Pythagoras' constant_. is the ratio of diagonal to side length in a square. ≈ 1.4142135623 7309504880 1688724209 6980785696 7187537694 8073176679 7379907324 7846210703 8850387534 3276415727 3501384623 0912297024 9248360558 5073721264 4121497099...
**1.41** | is also called _Pythagoras' constant_. is the ratio of diagonal to side length in a square. ≈ 1.4142135623 7309504880 1688724209 6980785696 7187537694 8073176679 7379907324 7846210703 8850387534 3276415727 3501384623 0912297024 9248360558 5073721264 4121497099...  One of the earliest numerical approximation of
One of the earliest numerical approximation of  2 was found on a Babylonian clay tablet (from the Yale Babylonian Collection), dated approximately to between 1800 B.C. and 1600 B.C. The annotations on this tablet give an impressive numerical approximation in four sexagesimal figures: 1 + 24/60 + 51/602 + 10/603 = 1.41421296... ≈ (Pn+1 - Pn)/Pn (P = Pell numbers) ≈ 17/12 ≈ 99/70 ≈ 1.0110101000001001111...2 = 2sinus(45°) = 2cosinus(45°) = 1 + (1 / (2 + (1 / (2 + (1 / (2 + ... )))))) = (
2 was found on a Babylonian clay tablet (from the Yale Babylonian Collection), dated approximately to between 1800 B.C. and 1600 B.C. The annotations on this tablet give an impressive numerical approximation in four sexagesimal figures: 1 + 24/60 + 51/602 + 10/603 = 1.41421296... ≈ (Pn+1 - Pn)/Pn (P = Pell numbers) ≈ 17/12 ≈ 99/70 ≈ 1.0110101000001001111...2 = 2sinus(45°) = 2cosinus(45°) = 1 + (1 / (2 + (1 / (2 + (1 / (2 + ... )))))) = ( _i_ + _i
_i_ + _i i_) / _i_ If you want to have some fun with
i_) / _i_ If you want to have some fun with  2: start with the very rough approximation 7/5. Then (7+5+5)/(7+5) = 17/12 (17+12+12)/(17+12) = 41/29 (41+29+29)/(41+29) = 99/70 (99+70+70)/(99+70) = 239/169 ... continuing closer approximations of
2: start with the very rough approximation 7/5. Then (7+5+5)/(7+5) = 17/12 (17+12+12)/(17+12) = 41/29 (41+29+29)/(41+29) = 99/70 (99+70+70)/(99+70) = 239/169 ... continuing closer approximations of  2 - posted by Larry Bickford - Writing numbers using only square roots of 2: 3 = -log2log2
2 - posted by Larry Bickford - Writing numbers using only square roots of 2: 3 = -log2log2 (
( (
( 2)) 4 = -log2log2
2)) 4 = -log2log2 (
( (
( (
( 2))) 5 = -log2log2
2))) 5 = -log2log2 (
( (
( (
( (
( 2)))) 6 = -log2log2
2)))) 6 = -log2log2 (
( (
( (
( (
( (
( 2))))) ... etc. ISO paper sizes are all based on a single aspect ratio of the square root of two, or approximately 1:1.4142. Basing paper upon this ratio was conceived by Georg Lichtenberg in 1786, and at the beginning of the 20th century, Dr Walter Porstmann turned Lichtenberg's idea into a proper system of different paper sizes. | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | |
|
2))))) ... etc. ISO paper sizes are all based on a single aspect ratio of the square root of two, or approximately 1:1.4142. Basing paper upon this ratio was conceived by Georg Lichtenberg in 1786, and at the beginning of the 20th century, Dr Walter Porstmann turned Lichtenberg's idea into a proper system of different paper sizes. | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | |
|  **1.62** | is the Golden Number, also called Golden Ratio or Phi. Golden Number property: (
**1.62** | is the Golden Number, also called Golden Ratio or Phi. Golden Number property: ( + 1)/
+ 1)/ =
=  /1 Fibonacci number sequence is intimately connected with the Golden Ratio.
/1 Fibonacci number sequence is intimately connected with the Golden Ratio.  The fraction 1/998999 contains Fibonacci numbers, i.e.: 1/998999=0.00000**1**00**1**00**2**00**3**00**5**00**8**0**13**0**21**0**34**0**55**0**89**...
The fraction 1/998999 contains Fibonacci numbers, i.e.: 1/998999=0.00000**1**00**1**00**2**00**3**00**5**00**8**0**13**0**21**0**34**0**55**0**89**...  Radii at 0° and approximately 222.49° divide a circle in the Golden Ratio: B/A =
Radii at 0° and approximately 222.49° divide a circle in the Golden Ratio: B/A =  /1 = (
/1 = ( 5 + 1)/2 = (
5 + 1)/2 = ( 4 +
4 +  (4! - 4))/4 = -2sin(666) ≈ Fn+1 / Fn (F = Fibonacci numbers) ≈ 1.61803 39887 49894 84820 45868 34365 63811... Remarkably, you can use Fibonacci successive terms to convert miles to kilometers: 8 miles ≈ 13 kilometers 13 miles ≈ 21 kilometers This works because the two units stand in the Golden Ratio (to within 0.5 percent). The last digit of the numbers in the Fibonacci Sequence are cyclic, they form a pattern that repeats after every 60th number: 0, 1, 1, 2, 3, 5, 8, 3, 1, 4, 5, 9, 4, 3, 7, 0, 7, 7, 4, 1, 5, 6, 1, 7, 8, 5, 3, 8, 1, 9, 0, 9, 9, 8, 7, 5, 2, 7, 9, 6, 5, 1, 6, 7, 3, 0, 3, 3, 6, 9, 5, 4, 9, 3, 2, 5, 7, 2, 9, 1. The 3184th Fibonacci number is an apocalypse number (Apocalpyse numbers are numbers having exactly 666 digits). | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | |
| **π2/6 1.64** | ≈ 1.644934066848226436472 The “**Basel Problem**” asks for the exact sum of the reciprocal square series: 1 + 1/22 + 1/32 + 1/42 + 1/52 + ... + 1/(_n_-1)2 + 1/_n_2 as well as a proof that this sum is correct. The Swiss mathematician **Euler** found the exact sum to be _**π**_**2/6** and announced this discovery in 1735. The value is denoted by _**λ**_ (lambda) and seems to appear everywhere in mathematics. In fact, the probability that a randomly chosen integer is not divisible by a square (square-free) is 1/_λ_ or 6/_π_2 | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | |
|
(4! - 4))/4 = -2sin(666) ≈ Fn+1 / Fn (F = Fibonacci numbers) ≈ 1.61803 39887 49894 84820 45868 34365 63811... Remarkably, you can use Fibonacci successive terms to convert miles to kilometers: 8 miles ≈ 13 kilometers 13 miles ≈ 21 kilometers This works because the two units stand in the Golden Ratio (to within 0.5 percent). The last digit of the numbers in the Fibonacci Sequence are cyclic, they form a pattern that repeats after every 60th number: 0, 1, 1, 2, 3, 5, 8, 3, 1, 4, 5, 9, 4, 3, 7, 0, 7, 7, 4, 1, 5, 6, 1, 7, 8, 5, 3, 8, 1, 9, 0, 9, 9, 8, 7, 5, 2, 7, 9, 6, 5, 1, 6, 7, 3, 0, 3, 3, 6, 9, 5, 4, 9, 3, 2, 5, 7, 2, 9, 1. The 3184th Fibonacci number is an apocalypse number (Apocalpyse numbers are numbers having exactly 666 digits). | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | |
| **π2/6 1.64** | ≈ 1.644934066848226436472 The “**Basel Problem**” asks for the exact sum of the reciprocal square series: 1 + 1/22 + 1/32 + 1/42 + 1/52 + ... + 1/(_n_-1)2 + 1/_n_2 as well as a proof that this sum is correct. The Swiss mathematician **Euler** found the exact sum to be _**π**_**2/6** and announced this discovery in 1735. The value is denoted by _**λ**_ (lambda) and seems to appear everywhere in mathematics. In fact, the probability that a randomly chosen integer is not divisible by a square (square-free) is 1/_λ_ or 6/_π_2 | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | |
|  **1.73** | is also known as _Theodorus' constant_ (it is named after Theodorus of Cyrene, who proved that the square roots of the numbers from 3 to 17, excluding 4, 9, and 16, are irrational). is the diagonal of a cube having 1-unit sides. is the height of an equilateral triangle having 2-unit sides. The shape 'Vesica piscis' (fish bladder) has a major axis/minor axis ratio equal to the square root of 3, this can be shown by constructing two equilateral triangles within it. ≈ 1.7320508075 6887729352 7446341505 8723669428 0525381038 0628055806 9794519330 1690880003 7081146186 7572485756 7562614141 5406703029 9699450949 9895247881 1655512094... = 2sinus(60°) = 2sinus(30°) = 1 + (1 / (**1 +** (1 / (**2 +** (1 / (**1** **+** (1 / **2** **+** ... ))))))) ≈ 97/56 ≈ 1.1011101101100111101...2 | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | |
| **2 ⠼⠃
**1.73** | is also known as _Theodorus' constant_ (it is named after Theodorus of Cyrene, who proved that the square roots of the numbers from 3 to 17, excluding 4, 9, and 16, are irrational). is the diagonal of a cube having 1-unit sides. is the height of an equilateral triangle having 2-unit sides. The shape 'Vesica piscis' (fish bladder) has a major axis/minor axis ratio equal to the square root of 3, this can be shown by constructing two equilateral triangles within it. ≈ 1.7320508075 6887729352 7446341505 8723669428 0525381038 0628055806 9794519330 1690880003 7081146186 7572485756 7562614141 5406703029 9699450949 9895247881 1655512094... = 2sinus(60°) = 2sinus(30°) = 1 + (1 / (**1 +** (1 / (**2 +** (1 / (**1** **+** (1 / **2** **+** ... ))))))) ≈ 97/56 ≈ 1.1011101101100111101...2 | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | |
| **2 ⠼⠃  ** | is the only even prime. is the first taxicab number (trivial). - posted by Charles Rathbone there are no integers x, y, and z for which x_n_ + y_n_ = z_n_ is valid, when _n_ is greater than **2** (see Fermat's last conjecture). _n_2 ± _n_ is always divisible by 2. 2 + 2 = 2 x 2 = 22 = 33 - 52 = 42 - 32 - 22 - 12 = (32 + 42 + 52 + 62 + 72 + 82 + 92)/ (12 + 22 + 32 + 42 + 52 + 62 + 72) =
** | is the only even prime. is the first taxicab number (trivial). - posted by Charles Rathbone there are no integers x, y, and z for which x_n_ + y_n_ = z_n_ is valid, when _n_ is greater than **2** (see Fermat's last conjecture). _n_2 ± _n_ is always divisible by 2. 2 + 2 = 2 x 2 = 22 = 33 - 52 = 42 - 32 - 22 - 12 = (32 + 42 + 52 + 62 + 72 + 82 + 92)/ (12 + 22 + 32 + 42 + 52 + 62 + 72) =  (2+
(2+ (2+
(2+ (2+
(2+ (2 + ... )))) ; Proof: if _N_ =
(2 + ... )))) ; Proof: if _N_ =  (2+(
(2+( 2+(
2+( 2+(
2+( ... )))) , then _N_2 = 2 +
... )))) , then _N_2 = 2 +  (2+
(2+ (2+
(2+ (2 + ... ))) = 2 + _N_ , solving _N_2 - _N_ - 2 = 0 , we find the positive solution _N_ = **2** =
(2 + ... ))) = 2 + _N_ , solving _N_2 - _N_ - 2 = 0 , we find the positive solution _N_ = **2** =  (3 + 2
(3 + 2 2) -
2) -  (3 - 2
(3 - 2 2) = 3
2) = 3 (6
(6 3 + 10) - 3
3 + 10) - 3 (6
(6 3 - 10) = loga a2 = tan(arcsin(cos(arctan(cos(arctan(
3 - 10) = loga a2 = tan(arcsin(cos(arctan(cos(arctan( 3)))))) =(1 + _i_)(1 - _i_) = X/V **2**5·92 = **2**592, the only 4-digit number of the form ABxCD=ABCD. The only other known number that shares this property is 24547284284866560000000000 = 24·54·72·84·28·48·66·56·00·00·00·00·00. Such numbers arec called narcissistic numbers. 2**7** = **7**12 - 1**7**3 is the smallest prime that can grow 7 times by the right: **2** is prime, **2**9 is prime, **2**93 is prime, **2**939 is prime, **2**9399 is prime, **2**93999 is prime, **2**939999 is prime. **2**9399999 is prime. Tetration: _nn_ = 2, when _n_ is about 1.559610469... (which is a transcendental number) When you increase the area of a square of 1 unit-square, the side _n_ of this square - for _n_ > 3 - increases approximately of 1/2n. For example:
3)))))) =(1 + _i_)(1 - _i_) = X/V **2**5·92 = **2**592, the only 4-digit number of the form ABxCD=ABCD. The only other known number that shares this property is 24547284284866560000000000 = 24·54·72·84·28·48·66·56·00·00·00·00·00. Such numbers arec called narcissistic numbers. 2**7** = **7**12 - 1**7**3 is the smallest prime that can grow 7 times by the right: **2** is prime, **2**9 is prime, **2**93 is prime, **2**939 is prime, **2**9399 is prime, **2**93999 is prime, **2**939999 is prime. **2**9399999 is prime. Tetration: _nn_ = 2, when _n_ is about 1.559610469... (which is a transcendental number) When you increase the area of a square of 1 unit-square, the side _n_ of this square - for _n_ > 3 - increases approximately of 1/2n. For example:  (12 + 122) ≈ 12 + 1/(2 x 12) ≈ 12.0416... - G. Sarcone Curiosity... An everyday example when 1 + 1 ≠ 2: 1 liter of water + 1 liter of alcohol = 1.926 liters of liquid "Liangyi" (Number 2), in the Mystical Numbers of Taoism, symbolizes the Twin, the First Division, the Duality of Opposites (Yin/Yang). In Cantonese the number two is fortunate, because it sounds similar to "easy" in the dialect. In pre-1972 Indonesian and Malay orthography, the digit 2 was shorthand for the reduplication that forms plurals, for instance: orang "person", and orang-orang or orang2 "people". This orthography has resurfaced widely in text messaging and other forms of electronic communication. The two-second rule is an easy way to make sure you have left enough following distance between your car and the vehicle in front, no matter what speed you're travelling at. To check if you are travelling two seconds behind the vehicle in front: - watch the vehicle in front of you pass a landmark (such as a sign, tree, or power pole) at the side of the road, - as it passes the landmark, start counting 'One thousand and one, one thousand and two', - if you pass the landmark before you finish saying those eight words, you are following too closely. Slow down, pick another landmark and repeat the words to make sure you have increased your following distance. -- Source Land Transport NZ. The most common two-letter words in order of frequency are: of, to, in, it, is, be, as, at, so, we, he, by, or, on, do, if, me, my, up, an, go, no, us, am. 'Skiing' is the only word in the English language with TWO i. A honey bee must tap TWO million flowers to make ONE pound of honey! "A man is a person who will pay two dollars for a one-dollar item he wants. A woman will pay one dollar for a two-dollar item she doesn't want..." -- William Binger TWO in different languages (© G. Sarcone) (Old English twā) Reconstructed proto-language: | * PAL | Indo-european | * DWI-, * DUWO- | Sanskrit |
(12 + 122) ≈ 12 + 1/(2 x 12) ≈ 12.0416... - G. Sarcone Curiosity... An everyday example when 1 + 1 ≠ 2: 1 liter of water + 1 liter of alcohol = 1.926 liters of liquid "Liangyi" (Number 2), in the Mystical Numbers of Taoism, symbolizes the Twin, the First Division, the Duality of Opposites (Yin/Yang). In Cantonese the number two is fortunate, because it sounds similar to "easy" in the dialect. In pre-1972 Indonesian and Malay orthography, the digit 2 was shorthand for the reduplication that forms plurals, for instance: orang "person", and orang-orang or orang2 "people". This orthography has resurfaced widely in text messaging and other forms of electronic communication. The two-second rule is an easy way to make sure you have left enough following distance between your car and the vehicle in front, no matter what speed you're travelling at. To check if you are travelling two seconds behind the vehicle in front: - watch the vehicle in front of you pass a landmark (such as a sign, tree, or power pole) at the side of the road, - as it passes the landmark, start counting 'One thousand and one, one thousand and two', - if you pass the landmark before you finish saying those eight words, you are following too closely. Slow down, pick another landmark and repeat the words to make sure you have increased your following distance. -- Source Land Transport NZ. The most common two-letter words in order of frequency are: of, to, in, it, is, be, as, at, so, we, he, by, or, on, do, if, me, my, up, an, go, no, us, am. 'Skiing' is the only word in the English language with TWO i. A honey bee must tap TWO million flowers to make ONE pound of honey! "A man is a person who will pay two dollars for a one-dollar item he wants. A woman will pay one dollar for a two-dollar item she doesn't want..." -- William Binger TWO in different languages (© G. Sarcone) (Old English twā) Reconstructed proto-language: | * PAL | Indo-european | * DWI-, * DUWO- | Sanskrit |  DVÎ |
DVÎ |  dvai (m) / dvā (f) / dve (n) Proto-Hellenic | * DWO | , Greek, Attic | ΔYO DUO | Latin | DVO, -Æ | , | BI- | , Archaic Latin | * DWO | , | * DWI- | Italian due; French deux; Spanish and Catalan dos; Provençal dous (m), dos (f); Portuguese dois (m), duas (f); Romanian doi (m), două (f); Romansh dus (m), duas (f); Sardinian dúos (m), dúas (f). Old Celtic | DO | Breton daou (m), div (f); Welsh dau (m), dwy (f); Irish a dó (cardinal), dhá (things), beirt (persons). Old Germanic | TWAIZ | Dutch twee; German zwei(often zwo is used to avoid confusion with drei, 3); Danish and Norwegian to; Swedish två; Icelandic tveir. Old Slavic | DUVA, DVE | Russian два dva; Czech dva; Slovenian dvá; Polish dwa. Proto Indo-Iranian | * DVA: | Persian دو do; Hindi दो d̪oː.
dvai (m) / dvā (f) / dve (n) Proto-Hellenic | * DWO | , Greek, Attic | ΔYO DUO | Latin | DVO, -Æ | , | BI- | , Archaic Latin | * DWO | , | * DWI- | Italian due; French deux; Spanish and Catalan dos; Provençal dous (m), dos (f); Portuguese dois (m), duas (f); Romanian doi (m), două (f); Romansh dus (m), duas (f); Sardinian dúos (m), dúas (f). Old Celtic | DO | Breton daou (m), div (f); Welsh dau (m), dwy (f); Irish a dó (cardinal), dhá (things), beirt (persons). Old Germanic | TWAIZ | Dutch twee; German zwei(often zwo is used to avoid confusion with drei, 3); Danish and Norwegian to; Swedish två; Icelandic tveir. Old Slavic | DUVA, DVE | Russian два dva; Czech dva; Slovenian dvá; Polish dwa. Proto Indo-Iranian | * DVA: | Persian دو do; Hindi दो d̪oː.  Evolution from 'seal script' to modern sinograph 二 : Old Chinese (pron.) | ñzhi | Chinese 二 èr (is used for numbers and in counting) / 两 liǎng (is used when counting objects or persons). Proto-Semitic | * ThNÂ | ; | KIL' | Semitic root | Th-N | , derived verb 'thny', to repeat. Ancient Egyptian [sn.-] sen; Akkadian
Evolution from 'seal script' to modern sinograph 二 : Old Chinese (pron.) | ñzhi | Chinese 二 èr (is used for numbers and in counting) / 两 liǎng (is used when counting objects or persons). Proto-Semitic | * ThNÂ | ; | KIL' | Semitic root | Th-N | , derived verb 'thny', to repeat. Ancient Egyptian [sn.-] sen; Akkadian  shénâ; Punic
shénâ; Punic  shnem. Arabic اِثنان ithna:n; Hebrew שתיים shtayim; Maltese: tnejn; Amharic hulät. More languagesMagyar kettő. Turkish iki. Mayan ca. Nahuatl ōme. Suomi kaksi. Zulu **(isi / ku)bili_**. HIDDEN ROOTSThe roots of the word two are hidden in the following words: balance, bezel, bicycle, binary, biscuit, combine, diploma, diptych, double, doubt, duel, duet, duplex, duplicate, pinochle; between, twist, twice, twill, twin; Mishnah. In French: bafouiller, berlue, besace, bévue, bigle, binocle, bisquer, brouette (< bis-rouette). | | | | |
|
shnem. Arabic اِثنان ithna:n; Hebrew שתיים shtayim; Maltese: tnejn; Amharic hulät. More languagesMagyar kettő. Turkish iki. Mayan ca. Nahuatl ōme. Suomi kaksi. Zulu **(isi / ku)bili_**. HIDDEN ROOTSThe roots of the word two are hidden in the following words: balance, bezel, bicycle, binary, biscuit, combine, diploma, diptych, double, doubt, duel, duet, duplex, duplicate, pinochle; between, twist, twice, twill, twin; Mishnah. In French: bafouiller, berlue, besace, bévue, bigle, binocle, bisquer, brouette (< bis-rouette). | | | | |
|  2.24** | is an irrational number involved in the formula for the Golden ratio. is also used in statistics when dealing with 5-business day weeks. is the hypothenuse of a right triangle having 1 and 2-unit sides. is the diagonal a rectangular box having 1,
2.24** | is an irrational number involved in the formula for the Golden ratio. is also used in statistics when dealing with 5-business day weeks. is the hypothenuse of a right triangle having 1 and 2-unit sides. is the diagonal a rectangular box having 1,  2 and
2 and  2-unit sides. = e_i
2-unit sides. = e_i + 2
+ 2 ≈ 2.2360679774 9978969640 9173668731 2762354406 1835961152 5724270897 2454105209 2563780489 9414414408 3787822749 6950817615 0773783504 2532677244 4707386358 6360121533... ≈ 85/38 ≈ 10.0011110001101111...2 | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | |
| e 2.72
≈ 2.2360679774 9978969640 9173668731 2762354406 1835961152 5724270897 2454105209 2563780489 9414414408 3787822749 6950817615 0773783504 2532677244 4707386358 6360121533... ≈ 85/38 ≈ 10.0011110001101111...2 | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | |
| e 2.72  | Discovered by the Scottish mathematician John Napier of Merchistoun. e stands for exponens (in Latin, 'exponential') = 1/0! + 1/1! + 1/2! + 1/3! + 1/4! + 1/5! + 1/6! + ... e ≈ (1001/1000)1000 e has this mathematical property: d(_e_x) dx = _e_x ≈ 2.7182818284 5904523536 0287471352 6624977572 4709369995 9574966967 6277240766 3035354759 4571382178 5251664274 2746639193 2003059921 8174135966 2904357290 0334295260... ≈ 6
| Discovered by the Scottish mathematician John Napier of Merchistoun. e stands for exponens (in Latin, 'exponential') = 1/0! + 1/1! + 1/2! + 1/3! + 1/4! + 1/5! + 1/6! + ... e ≈ (1001/1000)1000 e has this mathematical property: d(_e_x) dx = _e_x ≈ 2.7182818284 5904523536 0287471352 6624977572 4709369995 9574966967 6277240766 3035354759 4571382178 5251664274 2746639193 2003059921 8174135966 2904357290 0334295260... ≈ 6 (
( 4 +
4 +  5) (mathematical coincidence) Gaussian integral
5) (mathematical coincidence) Gaussian integral  e_ia_ = cos a + i sin a Ln x ≡ log**e** x log_x_ = log e · Ln_x Benjamin Peirce suggested the innovative notation, that looked like a paper clip, for e and
e_ia_ = cos a + i sin a Ln x ≡ log**e** x log_x_ = log e · Ln_x Benjamin Peirce suggested the innovative notation, that looked like a paper clip, for e and  shown below:
shown below:  From J. D. Runkin's Mathematical Monthly, vol. I, No. 5, Feb. 1859 | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | |
| 3 ⠼⠉
From J. D. Runkin's Mathematical Monthly, vol. I, No. 5, Feb. 1859 | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | |
| 3 ⠼⠉  | is the only prime 1 less than a perfect square. - Robin Regan is the number of spatial dimensions needed to mathematically describe a solid. are the primary colors. are the geometric constructions you cannot build using just a ruler and compasses: 1. You cannot trisect - divide into three equal parts - a given angle; 2. Double a cube; and 3. Square a circle. A number is divisible by 3 when the sum of its digits can be divided by 3. If the denominator of a rational number is not divisible by 3, then the repeating part of its decimal expansion is an integer divisible by 9. Example: 1/7 = 0.142857... has a repeating part '142857' divisible by 9. Another example with a larger recurring decimal: 1/23 = 0.0434782608695652173913... has a repeating part '0434782608695652173913' divisible by 9. 3 + 2 = log2 32 =
| is the only prime 1 less than a perfect square. - Robin Regan is the number of spatial dimensions needed to mathematically describe a solid. are the primary colors. are the geometric constructions you cannot build using just a ruler and compasses: 1. You cannot trisect - divide into three equal parts - a given angle; 2. Double a cube; and 3. Square a circle. A number is divisible by 3 when the sum of its digits can be divided by 3. If the denominator of a rational number is not divisible by 3, then the repeating part of its decimal expansion is an integer divisible by 9. Example: 1/7 = 0.142857... has a repeating part '142857' divisible by 9. Another example with a larger recurring decimal: 1/23 = 0.0434782608695652173913... has a repeating part '0434782608695652173913' divisible by 9. 3 + 2 = log2 32 =  (14 - 6
(14 - 6 5) +
5) +  5 (sum of two square roots) = 4! / (4 x
5 (sum of two square roots) = 4! / (4 x  4) = XV/V = CL/L = MD/D = 4 + 4 – 5 = 43 + 43 – 53 = 17,469 / 5,823 (this division contains all digits 1 through 9 once) 3 x 51249876 = 153749628 (the multiplication uses all 9 digits once - and so does its product!) 3 x 37 = 111 33 x 3367 = 111,111 333 x 333667 = 111,111,111 3333 x 33336667 = 111,111,111,111 33333 x 3333366667 = 111,111,111,111,111 3 x 1.5 = 3 + 1.5 32 = 3! + 3 32 = 52 - 42 33 = 63 - 53 - 43 33 = 32 + 32 + 32 34 x 425 = 34425 (see also 312 x 325 = 312325) 3 is the minimum colors needed to create camouflage patches, usually used in military compounds and vehicles. - posted by George Pantazis 38 31 36 33 35 37 34 39 32 The product of the 3 numbers in each row, column, or diagonal of the geometric magic square opposite - involving powers of 3 - gives the magic constant 14,348,907. Moreover, the exponents are arranged the same as in the normal 3x3 magic square! A 3 x 3 alphamagic square is a magic square for which the number of letters in the word for each number generates another magic square, for instance: 5 22 18 28 15 2 12 8 25 five (4) twenty-two (9) eighteen (8) twenty-eight (11) fifteen (7) two (3) twelve (6) eight (5) twenty-five (10) A 3 x 6 rectangle has an area equal to its perimeter. In one gram of water the number of molecules is about: 3.3 x 1022 = 33000000000000000000000 The balanced ternary base, is a numeral system which uses 3 values or digits: -1, 0, and 1. It works as follows (in the example, the symbol 1 denotes the digit -1): Decimal -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 Balanced ternary 110 111 11 10 11 1 0 1 11 10 11 111 110 111 Ternary or base-3 numbers can be converted to balanced ternary notation by adding 1111... with carry, then subtracting 1111... without borrow. For instance: 0213 + 1113 = 2023, 2023 - 1113 = 1113(bal) = 710 This non-standard positional numeral system is easily represented as electronic signals, as potential can either be negative, neutral, or positive (comparison logic). The balance ternary system is also useful to solve the classical 2-pan balance puzzle. The letters A, F, H, K, N, Y and Z are made up with 3 lines. In SMS language **<3** means 'I love you', and **<333**, 'I love you so much'. **3** hundred millions of Indians live with less than 1 dollar per day (2004). Non-paternity rates: statistically, one in **three** men who ask for paternity test turn out not to be the biological parent. An octopus has 3 hearts. The number 3 symbolizes the principle of growth. In Guangdong province, China, three is associated with living or giving birth. "Sanqing" (also known as "Sanxing" or "Sancai"), in the Mystical Numbers of Taoism, represents the number 3 and symbolizes the Three Luminaries: Sun, Moon, Stars. It also defines the concept of "Heaven, Mankind, Earth" as well as "Upper, Centre, Lower". Deep thought: "There are 3 kinds of people: those who can count and those who can't". Riddle 1: Spell 'mousetrap' in **3 letters**... Answer: C-A-T. Riddle 2: Spell 'water' in 3 letters... Answer: H-2-O. Joke: Chuck Norris once won a game of Connect Four in **3 moves**!
4) = XV/V = CL/L = MD/D = 4 + 4 – 5 = 43 + 43 – 53 = 17,469 / 5,823 (this division contains all digits 1 through 9 once) 3 x 51249876 = 153749628 (the multiplication uses all 9 digits once - and so does its product!) 3 x 37 = 111 33 x 3367 = 111,111 333 x 333667 = 111,111,111 3333 x 33336667 = 111,111,111,111 33333 x 3333366667 = 111,111,111,111,111 3 x 1.5 = 3 + 1.5 32 = 3! + 3 32 = 52 - 42 33 = 63 - 53 - 43 33 = 32 + 32 + 32 34 x 425 = 34425 (see also 312 x 325 = 312325) 3 is the minimum colors needed to create camouflage patches, usually used in military compounds and vehicles. - posted by George Pantazis 38 31 36 33 35 37 34 39 32 The product of the 3 numbers in each row, column, or diagonal of the geometric magic square opposite - involving powers of 3 - gives the magic constant 14,348,907. Moreover, the exponents are arranged the same as in the normal 3x3 magic square! A 3 x 3 alphamagic square is a magic square for which the number of letters in the word for each number generates another magic square, for instance: 5 22 18 28 15 2 12 8 25 five (4) twenty-two (9) eighteen (8) twenty-eight (11) fifteen (7) two (3) twelve (6) eight (5) twenty-five (10) A 3 x 6 rectangle has an area equal to its perimeter. In one gram of water the number of molecules is about: 3.3 x 1022 = 33000000000000000000000 The balanced ternary base, is a numeral system which uses 3 values or digits: -1, 0, and 1. It works as follows (in the example, the symbol 1 denotes the digit -1): Decimal -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 7 Balanced ternary 110 111 11 10 11 1 0 1 11 10 11 111 110 111 Ternary or base-3 numbers can be converted to balanced ternary notation by adding 1111... with carry, then subtracting 1111... without borrow. For instance: 0213 + 1113 = 2023, 2023 - 1113 = 1113(bal) = 710 This non-standard positional numeral system is easily represented as electronic signals, as potential can either be negative, neutral, or positive (comparison logic). The balance ternary system is also useful to solve the classical 2-pan balance puzzle. The letters A, F, H, K, N, Y and Z are made up with 3 lines. In SMS language **<3** means 'I love you', and **<333**, 'I love you so much'. **3** hundred millions of Indians live with less than 1 dollar per day (2004). Non-paternity rates: statistically, one in **three** men who ask for paternity test turn out not to be the biological parent. An octopus has 3 hearts. The number 3 symbolizes the principle of growth. In Guangdong province, China, three is associated with living or giving birth. "Sanqing" (also known as "Sanxing" or "Sancai"), in the Mystical Numbers of Taoism, represents the number 3 and symbolizes the Three Luminaries: Sun, Moon, Stars. It also defines the concept of "Heaven, Mankind, Earth" as well as "Upper, Centre, Lower". Deep thought: "There are 3 kinds of people: those who can count and those who can't". Riddle 1: Spell 'mousetrap' in **3 letters**... Answer: C-A-T. Riddle 2: Spell 'water' in 3 letters... Answer: H-2-O. Joke: Chuck Norris once won a game of Connect Four in **3 moves**!  If you’re a Simpsons fan, then you problably know about “Blinky”, the three-eyed fish found near the nuclear plant where Homer Simpson was working. As it turns out, the Simpsons were right yet again, as fishermen in Córdoba, Argentina caught a three-eyed wolf fish in a reservoir fed by a local nuclear power plan! (Fri, Oct 28, 2011)
If you’re a Simpsons fan, then you problably know about “Blinky”, the three-eyed fish found near the nuclear plant where Homer Simpson was working. As it turns out, the Simpsons were right yet again, as fishermen in Córdoba, Argentina caught a three-eyed wolf fish in a reservoir fed by a local nuclear power plan! (Fri, Oct 28, 2011)  In the taoist mythology, Erlang Shen (二郎神), or Erlang is a Chinese God with a **third truth-seeing eye** in the middle of his forehead. The French sentence 'un bonhomme haut comme trois pommes' (a **3**-apple-tall fellow) and the German sentence 'ein Kerlchen drei Käse hoch' (a **3**-cheese-tall fellow) mean both _a pint-sized guy/child_. "_Les fourmis, chacune d'elles ressemble au **chiffre 3**. Et il y en a! Il y en a 333333333333... jusqu'à l'infini_" (Jules Renard, 'Histoires naturelles'). Translation: "_The ants. Each of them resembles a **figure 3**. That's, it. There are 333333333333 to infinity_". 'Bookkeeper' and 'bookkeeping' are the only words in the English language with **three** consecutive double letters. The most common three-letter words in order of frequency are: the, and, for, are, but, not, you, all, any, can, had, her, was, one, our, out, day, get, has, him, his, how, man, new, now, old, see, two, way, who, boy, did, its, let, put, say, she, too, use. The name "Mitsubishi" (三菱) consists of two parts: "mitsu" meaning '**three**' and "bishi" meaning 'water caltrop', and hence 'rhombus', which is reflected in the company's famous logo (it is also translated as 'three diamonds'). Other Japanese family names containing the number 3: Mitsudani, Mitsugi, Mitsui, Mitsuhashi, Mitsude, Mitsuishi, Mitsumura, Mitsubori, Mitsumata, Mitsuyama, Mitsuzawa, Mitsuya, Mitsukuchi, Mitsukyou, Mitsuboshi, Mitsuzima, Mitsue, Mitsuike, Mitsuaichou, Mitsubuchi, Mitsuse, Mitsuyanagi, Mitsumachi, Mitsukunugi, Mitsuwa, Mitsuzaku, Mitsumatsu, Mitsuhuzi, Mitsuduka, Mitsuwari. **THREE** in different languages (© G. Sarcone) (Old English _**thrīe**_) Indo-european | * **TREYES**, * **TISORES**, * **TRI** | Sanskrit |
In the taoist mythology, Erlang Shen (二郎神), or Erlang is a Chinese God with a **third truth-seeing eye** in the middle of his forehead. The French sentence 'un bonhomme haut comme trois pommes' (a **3**-apple-tall fellow) and the German sentence 'ein Kerlchen drei Käse hoch' (a **3**-cheese-tall fellow) mean both _a pint-sized guy/child_. "_Les fourmis, chacune d'elles ressemble au **chiffre 3**. Et il y en a! Il y en a 333333333333... jusqu'à l'infini_" (Jules Renard, 'Histoires naturelles'). Translation: "_The ants. Each of them resembles a **figure 3**. That's, it. There are 333333333333 to infinity_". 'Bookkeeper' and 'bookkeeping' are the only words in the English language with **three** consecutive double letters. The most common three-letter words in order of frequency are: the, and, for, are, but, not, you, all, any, can, had, her, was, one, our, out, day, get, has, him, his, how, man, new, now, old, see, two, way, who, boy, did, its, let, put, say, she, too, use. The name "Mitsubishi" (三菱) consists of two parts: "mitsu" meaning '**three**' and "bishi" meaning 'water caltrop', and hence 'rhombus', which is reflected in the company's famous logo (it is also translated as 'three diamonds'). Other Japanese family names containing the number 3: Mitsudani, Mitsugi, Mitsui, Mitsuhashi, Mitsude, Mitsuishi, Mitsumura, Mitsubori, Mitsumata, Mitsuyama, Mitsuzawa, Mitsuya, Mitsukuchi, Mitsukyou, Mitsuboshi, Mitsuzima, Mitsue, Mitsuike, Mitsuaichou, Mitsubuchi, Mitsuse, Mitsuyanagi, Mitsumachi, Mitsukunugi, Mitsuwa, Mitsuzaku, Mitsumatsu, Mitsuhuzi, Mitsuduka, Mitsuwari. **THREE** in different languages (© G. Sarcone) (Old English _**thrīe**_) Indo-european | * **TREYES**, * **TISORES**, * **TRI** | Sanskrit |  **_TRÎ_** |
**_TRÎ_** |  _**trayaḥ**_ (m) / **_tisraḥ_** (f) / **_trīṇi_** (f) Greek, Attic | **TPEI**Σ, **TPIA** **_TRÊS_**, **_TRIA_** | Latin | **TRES**, **TRIA** | , Archaic Latin | * **TREIES** | Italian _**tre**_; French _**trois**_; Spanish and Catalan _**tres**_; Provençal _**trei**_, _**tres**_; Portuguese _**três**_; Romanian _**trei**_; Romansh _**trais**_; Sardinian _**très**_. Old Celtic | **TRI** | Breton **_tri_** (m), **_teir_** (f); Welsh **_tri_** (m), **_tair_** (f); Irish **_trí_** (m), **_teoir_** (f, old Irish), _**triúir**_ (people). Old Germanic | **THRIJIZ** | Dutch _**drie**_; German _**drei**_; Danish, Norwegian, and Swedish _**tre**_; Icelandic _**þrír**_. Old Slavic | **TRIJE**, **TRI** | Russian три _**tri**_; Czech _**tři**_; Slovenian **_trí_**; Polish _**trzy**_. Proto Indo-Iranian | * **TRAYAS** | Persian سه **_se_**; Hindi तीन **_t̪iːn_**.
_**trayaḥ**_ (m) / **_tisraḥ_** (f) / **_trīṇi_** (f) Greek, Attic | **TPEI**Σ, **TPIA** **_TRÊS_**, **_TRIA_** | Latin | **TRES**, **TRIA** | , Archaic Latin | * **TREIES** | Italian _**tre**_; French _**trois**_; Spanish and Catalan _**tres**_; Provençal _**trei**_, _**tres**_; Portuguese _**três**_; Romanian _**trei**_; Romansh _**trais**_; Sardinian _**très**_. Old Celtic | **TRI** | Breton **_tri_** (m), **_teir_** (f); Welsh **_tri_** (m), **_tair_** (f); Irish **_trí_** (m), **_teoir_** (f, old Irish), _**triúir**_ (people). Old Germanic | **THRIJIZ** | Dutch _**drie**_; German _**drei**_; Danish, Norwegian, and Swedish _**tre**_; Icelandic _**þrír**_. Old Slavic | **TRIJE**, **TRI** | Russian три _**tri**_; Czech _**tři**_; Slovenian **_trí_**; Polish _**trzy**_. Proto Indo-Iranian | * **TRAYAS** | Persian سه **_se_**; Hindi तीन **_t̪iːn_**.  Evolution from 'seal script' to modern sinograph 三 : Old Chinese (pron.) | **sâm** | Chinese 三 _**sān**._ The sinograph 叁 is used as a replacement for _sān_ on legal and financial documents to prevent fraud. Proto-Semitic | * **SALATh** | Semitic root | **Th-L-Th** | Ancient Egyptian [ḫmt'-] _**khemet**_; Akkadian _
Evolution from 'seal script' to modern sinograph 三 : Old Chinese (pron.) | **sâm** | Chinese 三 _**sān**._ The sinograph 叁 is used as a replacement for _sān_ on legal and financial documents to prevent fraud. Proto-Semitic | * **SALATh** | Semitic root | **Th-L-Th** | Ancient Egyptian [ḫmt'-] _**khemet**_; Akkadian _ _ _**shalash**_; Punic _
_ _**shalash**_; Punic _ **shlosht**_. Arabic ثلاثة _**thalathâ**_; Hebrew שלושה _**shlôshah**_; Maltese: _**tlieta**_; Amharic _**sost**_. More languagesMagyar _**három**_. Turkish _**üç**_. Mayan **_oxi'_**. Nahuatl _**ēyi**_. Suomi **_kolme_**. Zulu **_(ku)thathu_**. HIDDEN ROOTSThe roots of the word **three** are hidden in the following words: contest, detest, obtest, protest, sesterce, sitar, teapoy, tercet, tertian, tern, terpolymer, test, testament, testicle, testify, testimony, trammel, travel, trefoil, trench, trephine, trey, triad, triangle, triathlon, tribe, trio, triple, triplex, trine, trinity, trimurti, trivial, triumvir, trocar, troika; third, thrice. In French: travail, treillis, trémail. In Spanish: terliz, trabajo. Buy your favorite Number (3) here. | | | | | | | | | | | | | | |
|
**shlosht**_. Arabic ثلاثة _**thalathâ**_; Hebrew שלושה _**shlôshah**_; Maltese: _**tlieta**_; Amharic _**sost**_. More languagesMagyar _**három**_. Turkish _**üç**_. Mayan **_oxi'_**. Nahuatl _**ēyi**_. Suomi **_kolme_**. Zulu **_(ku)thathu_**. HIDDEN ROOTSThe roots of the word **three** are hidden in the following words: contest, detest, obtest, protest, sesterce, sitar, teapoy, tercet, tertian, tern, terpolymer, test, testament, testicle, testify, testimony, trammel, travel, trefoil, trench, trephine, trey, triad, triangle, triathlon, tribe, trio, triple, triplex, trine, trinity, trimurti, trivial, triumvir, trocar, troika; third, thrice. In French: travail, treillis, trémail. In Spanish: terliz, trabajo. Buy your favorite Number (3) here. | | | | | | | | | | | | | | |
|  **3.14**
**3.14**  | = Perimeter / Diagonal, of any circle. **Pi** expanded to 45 decimal places: 3.14159 26535 89793 23846 26433 83279 50288 41971 69399 **Pi** expanded to 52 binary places: 11.0010010000111 1110110101010 0010001000010 1101000111001 You cannot square a disc using just a ruler and compasses because
| = Perimeter / Diagonal, of any circle. **Pi** expanded to 45 decimal places: 3.14159 26535 89793 23846 26433 83279 50288 41971 69399 **Pi** expanded to 52 binary places: 11.0010010000111 1110110101010 0010001000010 1101000111001 You cannot square a disc using just a ruler and compasses because  is a transcendental number. Sondow formula for
is a transcendental number. Sondow formula for  , more formulas here.
, more formulas here.  = 4(1/1 - 1/3 + 1/5 - 1/7 + 1/9 - 1/11 + ... ) = 2(2/1 x 2/3 x 4/3 x 4/5 x 6/5 x 6/7 x 8/7 x 8/9 x ... ) ≈ 355/113 (a real good rational approximation of
= 4(1/1 - 1/3 + 1/5 - 1/7 + 1/9 - 1/11 + ... ) = 2(2/1 x 2/3 x 4/3 x 4/5 x 6/5 x 6/7 x 8/7 x 8/9 x ... ) ≈ 355/113 (a real good rational approximation of  ) ≈ (6
) ≈ (6 2)/5 In the late 18th century, James Stirling, a Scottish mathematician, developed an approximation for factorials using the transcendental numbers 'Pi' and 'e': _n_! ≈ (2
2)/5 In the late 18th century, James Stirling, a Scottish mathematician, developed an approximation for factorials using the transcendental numbers 'Pi' and 'e': _n_! ≈ (2 _n_)1/2 (_n_/e)_n_ The most famous formula for calculating Pi is Machin's formula:
_n_)1/2 (_n_/e)_n_ The most famous formula for calculating Pi is Machin's formula:  /4 = 4 arctan(1/5) – arctan(1/239) This formula, and similar ones, were used to push the accuracy of approximations to Pi to over 500 decimal places by the early 18th century (this was all hand calculation!). Amazing pandigital approximation of
/4 = 4 arctan(1/5) – arctan(1/239) This formula, and similar ones, were used to push the accuracy of approximations to Pi to over 500 decimal places by the early 18th century (this was all hand calculation!). Amazing pandigital approximation of  by mathematician E. Pegg: **0 + 3 + [1 - (9 - 8-5)-6]/(7 + 2-4)** A number or a formula is said to be "pandigital" if it contains each of the digits from 0 to 9. You can discuss this **here**. Interestingly, there are no occurrences of the sequence 123456 in the first million digits of Pi. - posted by George Pantazis Bamboozlement with Pi Does Pi equal 3? No? Then have a look on the algebraic equation below: x = (
by mathematician E. Pegg: **0 + 3 + [1 - (9 - 8-5)-6]/(7 + 2-4)** A number or a formula is said to be "pandigital" if it contains each of the digits from 0 to 9. You can discuss this **here**. Interestingly, there are no occurrences of the sequence 123456 in the first million digits of Pi. - posted by George Pantazis Bamboozlement with Pi Does Pi equal 3? No? Then have a look on the algebraic equation below: x = ( + 3)/2 2x =
+ 3)/2 2x =  + 3 2x(
+ 3 2x( - 3) = (
- 3) = ( + 3)(
+ 3)( - 3) 2
- 3) 2 x - 6x =
x - 6x =  2 - 9 9 - 6x =
2 - 9 9 - 6x =  2 - 2
2 - 2 x 9 - 6x + x2 =
x 9 - 6x + x2 =  2 - 2
2 - 2 x + x2 (3 - x)2 = (
x + x2 (3 - x)2 = ( - x)2 3 - x =
- x)2 3 - x =  - x 3 =
- x 3 =  We use Pi to: - describe the DNA double helix, - determining the distribution of primes - the probability that two randomly selected integers are relatively prime (i.e. have no common factors) is 6 / p2, - analyzing the ripples on water, - checking for accuracy - as there are now millions upon millions of known decimal places of Pi, by asking a super computer to compute this many figures its accuracy can be tested, - in cryptography - the science of coding, - generate of a random number. On _**Pi Day**_ (March 14 or 3-14) in 1879, a baby was born in Ulm, Germany to a German couple whose name meant "one stone". That baby was Albert Einstein!
We use Pi to: - describe the DNA double helix, - determining the distribution of primes - the probability that two randomly selected integers are relatively prime (i.e. have no common factors) is 6 / p2, - analyzing the ripples on water, - checking for accuracy - as there are now millions upon millions of known decimal places of Pi, by asking a super computer to compute this many figures its accuracy can be tested, - in cryptography - the science of coding, - generate of a random number. On _**Pi Day**_ (March 14 or 3-14) in 1879, a baby was born in Ulm, Germany to a German couple whose name meant "one stone". That baby was Albert Einstein!  occurs naturally in tables of death, in what is known as a Gaussian distribution of deaths in a population; that is, when a person dies, the event 'feels' Pi. The symbol for Pi was introduced by the English mathematician William Jones in 1706. Mathematician John Conway pointed out that if you break down the digits of Pi into blocks of ten, the probability that one of those blocks will contain ten distinct digits is about one in 40,000. Curiously, this first happens in the 7th block of ten digits. There is the little rhyme to help the memorisation of twenty-one digits of
occurs naturally in tables of death, in what is known as a Gaussian distribution of deaths in a population; that is, when a person dies, the event 'feels' Pi. The symbol for Pi was introduced by the English mathematician William Jones in 1706. Mathematician John Conway pointed out that if you break down the digits of Pi into blocks of ten, the probability that one of those blocks will contain ten distinct digits is about one in 40,000. Curiously, this first happens in the 7th block of ten digits. There is the little rhyme to help the memorisation of twenty-one digits of  : _Now, I wish I could recollect pi. "Eureka," cried the great inventor. Christmas Pudding; Christmas Pie Is the problem's very center._ Joke: A round pizza with radius 'z' and thickness 'a' has the volume **Pi·z·z·a**. | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | |
| **_S_ 3.24** | 3.246979603717467... is the Silver Number or silver constant given by: x3 - 5x2 + 6x - 1 = 0 **_S_** = 3
: _Now, I wish I could recollect pi. "Eureka," cried the great inventor. Christmas Pudding; Christmas Pie Is the problem's very center._ Joke: A round pizza with radius 'z' and thickness 'a' has the volume **Pi·z·z·a**. | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | |
| **_S_ 3.24** | 3.246979603717467... is the Silver Number or silver constant given by: x3 - 5x2 + 6x - 1 = 0 **_S_** = 3 7 + (7 · 3
7 + (7 · 3 7 + (7 · 3
7 + (7 · 3 7 + ... )) | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | |
| **4 ⠼⠙
7 + ... )) | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | | |
| **4 ⠼⠙  ** |
** |  is the smallest number of colors sufficient to color all planar maps with no adjoining countries sharing the same color. are the number of coordinates needed to describe an event in 'spacetime': t, x, y, z. Pick any whole number... If the number is even, divide it by 2; if it is odd, multiply it by 3, then add 1. By repeating this procedure, sooner or later you'll arrive at the number **4**, which will give you 2, which in turn gives you 1, and then get a 4 again! No matter what number you choose, you'll always arrive at the **4**-2-1 cycle. The word 'four' has 4 letters and is the smallest honest number. Honest numbers are numbers _n_ that can be described using exactly _n_ letters in standard mathematical English. A 4 x 4 square has an area equal to its perimeter. The only solution of xy = xy involving integers is: x = y = 2, and xy = xy = **4** **4**2 = 2**4**, is the solution to the equation _ab_ = _ba_, for _a_
is the smallest number of colors sufficient to color all planar maps with no adjoining countries sharing the same color. are the number of coordinates needed to describe an event in 'spacetime': t, x, y, z. Pick any whole number... If the number is even, divide it by 2; if it is odd, multiply it by 3, then add 1. By repeating this procedure, sooner or later you'll arrive at the number **4**, which will give you 2, which in turn gives you 1, and then get a 4 again! No matter what number you choose, you'll always arrive at the **4**-2-1 cycle. The word 'four' has 4 letters and is the smallest honest number. Honest numbers are numbers _n_ that can be described using exactly _n_ letters in standard mathematical English. A 4 x 4 square has an area equal to its perimeter. The only solution of xy = xy involving integers is: x = y = 2, and xy = xy = **4** **4**2 = 2**4**, is the solution to the equation _ab_ = _ba_, for _a_  _b_. Solution to Brocard's problem _**n**_**! + 1 = _m_2** : **4**! + 1 = 52 , the only other pairs are: 5! + 1 = 112 and 7! + 1 = 712 x2 - y2 is divisible by **4** only when (x - y) is even. Any integer of the form _n_**4** + **4** is not a prime, except for _n_=1, because it can be factorized as follows: _n_**4** + **4** = (_n_2 - 2_n_ + 2)(_n_2 + 2_n_ + 2) (_Aurifeuillean_ factorization) _n_**4** always ends with digits 0, 1, 5 or 6. Any prime of the form **4**_k_ + 1 is the sum of two square numbers:13 = **4** x 3 + 1 = 22 + 32 ; 73 = **4** x 18 + 1 = 32 + 82 ; 137 = **4** x 34 + 1 = 42 + 112 = 32 - 22 - 12 =
_b_. Solution to Brocard's problem _**n**_**! + 1 = _m_2** : **4**! + 1 = 52 , the only other pairs are: 5! + 1 = 112 and 7! + 1 = 712 x2 - y2 is divisible by **4** only when (x - y) is even. Any integer of the form _n_**4** + **4** is not a prime, except for _n_=1, because it can be factorized as follows: _n_**4** + **4** = (_n_2 - 2_n_ + 2)(_n_2 + 2_n_ + 2) (_Aurifeuillean_ factorization) _n_**4** always ends with digits 0, 1, 5 or 6. Any prime of the form **4**_k_ + 1 is the sum of two square numbers:13 = **4** x 3 + 1 = 22 + 32 ; 73 = **4** x 18 + 1 = 32 + 82 ; 137 = **4** x 34 + 1 = 42 + 112 = 32 - 22 - 12 =  (20 -
(20 -  (20 -
(20 -  (20 -
(20 -  (20 - ... )))) = 1(1/2)0 + 2(1/2)1 + 3(1/2)2 + 4(1/2)3 + 5(1/2)4 + 6(1/2)5 + ... 16/64 = 1
(20 - ... )))) = 1(1/2)0 + 2(1/2)1 + 3(1/2)2 + 4(1/2)3 + 5(1/2)4 + 6(1/2)5 + ... 16/64 = 16/64 = 1/4 If you multiply the number 21978 by 4, it turns backwards! = 15,768 / 3,942 (contains all digits 1 through 9 once) = CD/C The two equalities 4 x 1738 = 6952 and 4 x 1963 = 7852, use the digits 1-9 exactly once! An intriguing 4 x 4 magic square (fig. 1) that works just as well upside-down (fig. 2): fig. 1 I8 99 86 6I 66 8I 98 I9 9I I6 69 88 89 68 II 96 96 II 89 68 88 69 9I I6 6I 86 I8 99 I9 98 66 8I fig. 2 4 is the smallest digit that never occurs in any term of the "look-and-say" sequence. The Shadok's numbers are a kind of quaternary or **base-4** numeration system: 0 is Ga  4 is Buga
4 is Buga  8 is Zoga
8 is Zoga  12 is Meuga
12 is Meuga  1 is Bu
1 is Bu  5 is Bubu
5 is Bubu  9 is Zobu
9 is Zobu  13 is Meubu
13 is Meubu  2 is Zo
2 is Zo  6 is Buzo
6 is Buzo  10 is Zozo
10 is Zozo  14 is Meuzo
14 is Meuzo  3 is Meu
3 is Meu  7 is Bumeu
7 is Bumeu  11 is Zomeu
11 is Zomeu  15 is Meumeu
15 is Meumeu  The digit 4 on an LCD calculator is made up of 4 bars. A famous riddle: Show how one-half of five is four! Answer: Take off the first and last letters and you have the roman numeral for 4. The Roman numeral for four is **IV** (whose letters are one-half of the four letters in the spelled-out word "five"). Why is the Roman numeral **IIII** used instead of **IV** on clocks and watches? - using IIII brings more symmetry and balance to the dial. The IIII offsets the heavy VIII that is found on the other side. - the strict use of IV instead of IIII wasn't common until after the middle ages (the practice of placing smaller digits before large ones to indicate subtraction came into popularity in Europe after the invention of the printing press), the Romans generally used IIII. Clocks and watches are patterned after sundials, which were in use long before the middle ages. **Berger’s 4:9 theory**
The digit 4 on an LCD calculator is made up of 4 bars. A famous riddle: Show how one-half of five is four! Answer: Take off the first and last letters and you have the roman numeral for 4. The Roman numeral for four is **IV** (whose letters are one-half of the four letters in the spelled-out word "five"). Why is the Roman numeral **IIII** used instead of **IV** on clocks and watches? - using IIII brings more symmetry and balance to the dial. The IIII offsets the heavy VIII that is found on the other side. - the strict use of IV instead of IIII wasn't common until after the middle ages (the practice of placing smaller digits before large ones to indicate subtraction came into popularity in Europe after the invention of the printing press), the Romans generally used IIII. Clocks and watches are patterned after sundials, which were in use long before the middle ages. **Berger’s 4:9 theory**  In his book "Bauwerk und Plastik des Parthenon, in Antike Kunst" (Basel, 1980). E. Berger presents a study that investigates the way that the Pythagorean ideas of ratios of small numbers were used in the construction of the Temple of Athena Parthenos. In his opinion the ratio 4 : 9 were fundamental to the construction. A basic rectangle of sides 4 and 9 was constructed from three rectangles of sides 3 and 4 with diagonal 5 (see drawing). This form of construction also meant that the 3-4-5 Pythagorean triangle could be used to good effect to ensure that right angles in the building were accurately determined. The length of the Temple of Athena Parthenos is 69.5 m, its width is 30.88 m and the height at the cornice is 13.72 m. To a fairly high degree of accuracy this means that the ratio width : length = 4 : 9 while also the ratio height : width = 4 : 9. - Source: **Article** by J.J. O'Connor and E.F. Robertson. The **four-second rule** is the amount of time that internet user will wait for a page to load before leaving and going to another site. **Swear number**: The phrase "**four-letter word**" is used to describe most swear words in the English language. The Pythagorean oath, as quoted by the Renaissance magician Cornelius Agrippa, is as follows: "_I with pure mind by the **number four** do swear; That's holy, and the fountain of nature Eternal, parent of the mind..._" In Japan and in most Asiatic cultures, the number 4 (sinograph: 四) is considered unlucky because it is prounounced _**shi**_ which sounds like the word 'death'. Due to that, many numbered product lines skip the number 4. However, in some cases the word _yon_ ('4' in early classical Japanese) is used instead of _shi_: when counting floors in a building, or when you are asked "which floor?" in an elevator... The aversion or fear of the number 4 is called "Tetraphobia". Math-trick: Four equals three! Suppose: a + b = c . This can also be written as: 4a - 3a + 4b - 3b = 4c - 3c . After reorganizing: 4a + 4b - 4c = 3a + 3b - 3c . Take the constants out of the brackets: 4(a + b - c) = 3(a + b - c) . Remove the same term left and right, then: **4 = 3** Where is the error? Challenge: using **four 4's** and any operations, try to write equations that have the integers from 1 to 100 as the answer (see example below): 1 = 44/44 2 = 4/4 + 4/4 3 = (4 + 4 + 4)/4 4 = 4(4 - 4) + 4, etc... (click here to see solutions) Curiosity: Think of any number and write it out in WORDS. Count the number of letters it contains and write that down in WORDS. And so on: • TWENTY-EIGHT (11 letters) -> • ELEVEN (6 letters) -> • SIX (3 letters) -> • THREE (5 letters) -> • FIVE (4 letters) -> • FOUR (4 letters) -> etc. You will always arrive at FOUR! A dollar bill can be double folded (forward and backwards) 4x103 times before it will tear. STA4NCE = For instance! In Italian, the expression in quattro e quattr'otto (in four and four eight) means 'in a trice'. An amusing Finnish word that contains 4 y: Yötyöhyöty (advantage gained from working night shifts with the correspondingly higher salary). - posted by Juhani Sirkiä 4 rivers are mentioned in the Old Testament, Gen 2, 10: "And a river went out of Eden ... and parted ... into four heads. The ... first [is] Pison ... which compasses the whole land of Havilah ... the second [is] Gihon ... that compasses the whole land of Ethiopia ... the third [is] Hiddekel ... that goes toward the east of Assyria ... and the fourth [is] Euphrates that goes eastward to Assyria". The number 4 symbolizes the principle of putting ideas into form. It signifies work and productivity. 1 in 4 people worldwide is Muslim, and 2 out of 3 of the world's Muslims are in Asia (data: 2009). "Sixiang" (Number 4), in the Mystical Numbers of Taoism, represents the Four Essences: Earth, Water, Air, Fire. The most common four-letter words in order of frequency are: that, with, have, this, will, your, from, they, know, want, been, good, much, some, time, very, when, come, here, just, like, long, make, many, more, only, over, such, take, than, them, well, were. There are only 4 words in the English language which end in 'dous': hazardous, horrendous, stupendous and tremendous. FOUR in different languages (© G. Sarcone) (from Old English feower) Indo-european | * KWETORES, * KWETESRES | Sanskrit |
In his book "Bauwerk und Plastik des Parthenon, in Antike Kunst" (Basel, 1980). E. Berger presents a study that investigates the way that the Pythagorean ideas of ratios of small numbers were used in the construction of the Temple of Athena Parthenos. In his opinion the ratio 4 : 9 were fundamental to the construction. A basic rectangle of sides 4 and 9 was constructed from three rectangles of sides 3 and 4 with diagonal 5 (see drawing). This form of construction also meant that the 3-4-5 Pythagorean triangle could be used to good effect to ensure that right angles in the building were accurately determined. The length of the Temple of Athena Parthenos is 69.5 m, its width is 30.88 m and the height at the cornice is 13.72 m. To a fairly high degree of accuracy this means that the ratio width : length = 4 : 9 while also the ratio height : width = 4 : 9. - Source: **Article** by J.J. O'Connor and E.F. Robertson. The **four-second rule** is the amount of time that internet user will wait for a page to load before leaving and going to another site. **Swear number**: The phrase "**four-letter word**" is used to describe most swear words in the English language. The Pythagorean oath, as quoted by the Renaissance magician Cornelius Agrippa, is as follows: "_I with pure mind by the **number four** do swear; That's holy, and the fountain of nature Eternal, parent of the mind..._" In Japan and in most Asiatic cultures, the number 4 (sinograph: 四) is considered unlucky because it is prounounced _**shi**_ which sounds like the word 'death'. Due to that, many numbered product lines skip the number 4. However, in some cases the word _yon_ ('4' in early classical Japanese) is used instead of _shi_: when counting floors in a building, or when you are asked "which floor?" in an elevator... The aversion or fear of the number 4 is called "Tetraphobia". Math-trick: Four equals three! Suppose: a + b = c . This can also be written as: 4a - 3a + 4b - 3b = 4c - 3c . After reorganizing: 4a + 4b - 4c = 3a + 3b - 3c . Take the constants out of the brackets: 4(a + b - c) = 3(a + b - c) . Remove the same term left and right, then: **4 = 3** Where is the error? Challenge: using **four 4's** and any operations, try to write equations that have the integers from 1 to 100 as the answer (see example below): 1 = 44/44 2 = 4/4 + 4/4 3 = (4 + 4 + 4)/4 4 = 4(4 - 4) + 4, etc... (click here to see solutions) Curiosity: Think of any number and write it out in WORDS. Count the number of letters it contains and write that down in WORDS. And so on: • TWENTY-EIGHT (11 letters) -> • ELEVEN (6 letters) -> • SIX (3 letters) -> • THREE (5 letters) -> • FIVE (4 letters) -> • FOUR (4 letters) -> etc. You will always arrive at FOUR! A dollar bill can be double folded (forward and backwards) 4x103 times before it will tear. STA4NCE = For instance! In Italian, the expression in quattro e quattr'otto (in four and four eight) means 'in a trice'. An amusing Finnish word that contains 4 y: Yötyöhyöty (advantage gained from working night shifts with the correspondingly higher salary). - posted by Juhani Sirkiä 4 rivers are mentioned in the Old Testament, Gen 2, 10: "And a river went out of Eden ... and parted ... into four heads. The ... first [is] Pison ... which compasses the whole land of Havilah ... the second [is] Gihon ... that compasses the whole land of Ethiopia ... the third [is] Hiddekel ... that goes toward the east of Assyria ... and the fourth [is] Euphrates that goes eastward to Assyria". The number 4 symbolizes the principle of putting ideas into form. It signifies work and productivity. 1 in 4 people worldwide is Muslim, and 2 out of 3 of the world's Muslims are in Asia (data: 2009). "Sixiang" (Number 4), in the Mystical Numbers of Taoism, represents the Four Essences: Earth, Water, Air, Fire. The most common four-letter words in order of frequency are: that, with, have, this, will, your, from, they, know, want, been, good, much, some, time, very, when, come, here, just, like, long, make, many, more, only, over, such, take, than, them, well, were. There are only 4 words in the English language which end in 'dous': hazardous, horrendous, stupendous and tremendous. FOUR in different languages (© G. Sarcone) (from Old English feower) Indo-european | * KWETORES, * KWETESRES | Sanskrit |  CATÙR |
CATÙR |  catvāraḥ / catasraḥ / catvāri Proto-Hellenic | * QWET(O)RO- | Greek, Attic | τέτταρες, τέτταρα TETTARES, TETTARA | Latin | QUATTUOR | , Archaic Latin | * QUATBORO | Italian quattro; French, Provençal and Catalan quatre; Spanish cuatro; Portuguese quatro; Romanian patru; Romansh quatter; Sardinian bàtero. Old Celtic | PETOR | Breton pevar (m), peder (f); Welsh pedwar (m), pedair (f); Irish a ceathair (cardinal), ceathre (things), ceathrar (people). Old Germanic | FITHWOR | Dutch and German vier; Danish, Norwegian, and Swedish fire; Icelandic fjórir. Old Slavic | CETYRIJE, CETYRI | Russian четыре chetyrye; Czech čtyři; Slovenian štíri; Polish cztery. Proto Indo-Iranian | *K'ATWA:RAS | Persian چهار chahar; Hindi चार chaːr.
catvāraḥ / catasraḥ / catvāri Proto-Hellenic | * QWET(O)RO- | Greek, Attic | τέτταρες, τέτταρα TETTARES, TETTARA | Latin | QUATTUOR | , Archaic Latin | * QUATBORO | Italian quattro; French, Provençal and Catalan quatre; Spanish cuatro; Portuguese quatro; Romanian patru; Romansh quatter; Sardinian bàtero. Old Celtic | PETOR | Breton pevar (m), peder (f); Welsh pedwar (m), pedair (f); Irish a ceathair (cardinal), ceathre (things), ceathrar (people). Old Germanic | FITHWOR | Dutch and German vier; Danish, Norwegian, and Swedish fire; Icelandic fjórir. Old Slavic | CETYRIJE, CETYRI | Russian четыре chetyrye; Czech čtyři; Slovenian štíri; Polish cztery. Proto Indo-Iranian | *K'ATWA:RAS | Persian چهار chahar; Hindi चार chaːr.  Evolution from 'seal script' to modern sinograph 四 : Old Chinese (pron.) | si | Chinese 四 sí. Proto-Semitic | * RABA' | Semitic root | RB' | Ancient Egyptian [ỉfd'-] aft'u; Akkadian
Evolution from 'seal script' to modern sinograph 四 : Old Chinese (pron.) | si | Chinese 四 sí. Proto-Semitic | * RABA' | Semitic root | RB' | Ancient Egyptian [ỉfd'-] aft'u; Akkadian  or
or  erbe; Punic
erbe; Punic  'arbah. Arabic أربعة arba'â; Hebrew ארבעה ârba'ah; Maltese: erbgħa; Amharic arat. More languagesMagyar négy. Turkish dört. Mayan can. Nahuatl nāhui. Suomi neljä. Zulu (ku)ne. HIDDEN ROOTSThe roots of the word four are hidden in the following words: cadre, cahier, carillon, carnet, carrefour, casern, czardas, escadrille, petorritum, quadrant, quadriga, quadroon, quarantine, quarrel, quarry, quarter, quartan, quaternay, quatrain, quire, squad, square, tetrad, trapezium, trocar; farthing, filler, firking; rabi, arroba (from Arabic الربع ar-rub', "quarter"). In French: carreau, écarquiller, écarter, Périgord (< *_petru-corii_, 'four troops'), Périgueux, arrobase. In Italian: quadrivio, squadra, squartare, tessera. In Spanish: ejedrez, from Sanskrit चतुरङ्ग; caturaṅga, "having four limbs or parts". Gaulish person names: Petrullus, Petrogenos, Petrusonia ‘fourth born’ (< *_petuares_ / _petru-_, 'four'). Buy your favorite Number (4) here. | | | | | | | | | | | | |
| **5 ⠼⠑** V **
'arbah. Arabic أربعة arba'â; Hebrew ארבעה ârba'ah; Maltese: erbgħa; Amharic arat. More languagesMagyar négy. Turkish dört. Mayan can. Nahuatl nāhui. Suomi neljä. Zulu (ku)ne. HIDDEN ROOTSThe roots of the word four are hidden in the following words: cadre, cahier, carillon, carnet, carrefour, casern, czardas, escadrille, petorritum, quadrant, quadriga, quadroon, quarantine, quarrel, quarry, quarter, quartan, quaternay, quatrain, quire, squad, square, tetrad, trapezium, trocar; farthing, filler, firking; rabi, arroba (from Arabic الربع ar-rub', "quarter"). In French: carreau, écarquiller, écarter, Périgord (< *_petru-corii_, 'four troops'), Périgueux, arrobase. In Italian: quadrivio, squadra, squartare, tessera. In Spanish: ejedrez, from Sanskrit चतुरङ्ग; caturaṅga, "having four limbs or parts". Gaulish person names: Petrullus, Petrogenos, Petrusonia ‘fourth born’ (< *_petuares_ / _petru-_, 'four'). Buy your favorite Number (4) here. | | | | | | | | | | | | |
| **5 ⠼⠑** V ** ** |
** |  is the only prime number that ends in 5. is the number of Platonic solids. is the only prime number that ends in 5. is a congruent number because it is the area of a 20/3, 3/2, 41/6 triangle (a congruent number is an integer that is the area of a right triangle with three rational number sides). The Roman numeral for 5 is **V**, which comes from a representation of an outstretched hand. Any power of 5 ends in a 5 (except 50). = 32 - 22 = 12 + 22 = 25 - 33 52 = 2**5** 52 = 32 + 42 = 132 - 122 = (11 x 11 - 11)/(11 + 11) = D/C 19/95 = 1
is the only prime number that ends in 5. is the number of Platonic solids. is the only prime number that ends in 5. is a congruent number because it is the area of a 20/3, 3/2, 41/6 triangle (a congruent number is an integer that is the area of a right triangle with three rational number sides). The Roman numeral for 5 is **V**, which comes from a representation of an outstretched hand. Any power of 5 ends in a 5 (except 50). = 32 - 22 = 12 + 22 = 25 - 33 52 = 2**5** 52 = 32 + 42 = 132 - 122 = (11 x 11 - 11)/(11 + 11) = D/C 19/95 = 19/95 = 1/5 26/65 = 26/65 = 2/5 (**5** - 1)! + 1 = 0 (mod **5**2) Any number having a _abc_**5**_abc_**5** pattern is divisible by: 5, 73, 137, and 10001 **Can you count in 'ding-bong'?**  The inhabitants of 'Fongaponga' use a series of sounds made from this strange device to represent numbers: '**ding**' with the handbell, '**eek**' when squeezing the rubber bulb of the horn, and '**bong**' when beating the tambourine with the small ball. These very special **base-5 numerals** are then strings made from 3 sounds each corresponding to an additive numerical value. Looking at the number list below, we can guess with the help of some logic that 'eek' is actually a 'function' that indicates subtraction and that every 'ding' equals 5, and every 'bong', 7. 1. **ding-ding-ding** **-eek-** **bong-bong** 2. **bong** **-eek-** **ding** 3. **ding-ding** **-eek-** **bong** 4. **bong-bong** **-eek-** **ding-ding** 5. **ding** 6. **ding-ding-ding-ding** **-eek-** **bong-bong** 7. **bong** 8. **ding-ding-ding** **-eek-** **bong** 9. **bong-bong** **-eek-** **ding** 10. **ding-ding** 11. **bong-bong-** **bong** **-eek-** **ding-ding** 12. **ding-** **bong** 13. **ding-ding-ding-ding** **-eek-** **bong** 14. **bong-bong** 15. **ding-ding-ding** 16. **bong-bong-** **bong** **-eek-** **ding** 17. **ding-** **ding-** **bong** 18. **bong-bong-** **bong** **-** **bong** **-eek-** **ding-ding**19. **ding-bong-bong** 20. **ding-ding-ding** **-ding**21. **bong-bong-** **bong**22. **ding-ding-ding** **-** **bong** 23. **ding-ding-ding-ding-ding-ding** **-eek-** **bong**24. **ding-ding-** **bong-bong** _From number 24 on, all numbers are only combinations of **dings** and/or **bongs**._25. **d-d-d-d-d** 26. **d**-**b-b-b** 27. **d-** **d-d-d-** **b** 28. **b-b-b-b** 29. **d-d-d-b-b** 30. **d-d-d-d-d-d**... **Source:** - Sarcone's **"ding-bong numbers"** are sequence A102701 in the 'Encyclopedia of integer sequences'. - **"Fongaponga"**, Focus BrainTrainer nr. 7, page 51. A five-sided polygon (pentagon) has 5 diagonals. This is the only shape for which the number of sides and diagonals is the same (which may explain why _pentagrams_, _pentacles_, and _pentangles_ are so common and appear so often as iconographic symbols). - by Patrick Vennebush - _Pentagram_, _Pentangle_ and _Pentacle_ are all names for a 5-pointed star. This mystical symbol is supposed to keep away devils and witches.
The inhabitants of 'Fongaponga' use a series of sounds made from this strange device to represent numbers: '**ding**' with the handbell, '**eek**' when squeezing the rubber bulb of the horn, and '**bong**' when beating the tambourine with the small ball. These very special **base-5 numerals** are then strings made from 3 sounds each corresponding to an additive numerical value. Looking at the number list below, we can guess with the help of some logic that 'eek' is actually a 'function' that indicates subtraction and that every 'ding' equals 5, and every 'bong', 7. 1. **ding-ding-ding** **-eek-** **bong-bong** 2. **bong** **-eek-** **ding** 3. **ding-ding** **-eek-** **bong** 4. **bong-bong** **-eek-** **ding-ding** 5. **ding** 6. **ding-ding-ding-ding** **-eek-** **bong-bong** 7. **bong** 8. **ding-ding-ding** **-eek-** **bong** 9. **bong-bong** **-eek-** **ding** 10. **ding-ding** 11. **bong-bong-** **bong** **-eek-** **ding-ding** 12. **ding-** **bong** 13. **ding-ding-ding-ding** **-eek-** **bong** 14. **bong-bong** 15. **ding-ding-ding** 16. **bong-bong-** **bong** **-eek-** **ding** 17. **ding-** **ding-** **bong** 18. **bong-bong-** **bong** **-** **bong** **-eek-** **ding-ding**19. **ding-bong-bong** 20. **ding-ding-ding** **-ding**21. **bong-bong-** **bong**22. **ding-ding-ding** **-** **bong** 23. **ding-ding-ding-ding-ding-ding** **-eek-** **bong**24. **ding-ding-** **bong-bong** _From number 24 on, all numbers are only combinations of **dings** and/or **bongs**._25. **d-d-d-d-d** 26. **d**-**b-b-b** 27. **d-** **d-d-d-** **b** 28. **b-b-b-b** 29. **d-d-d-b-b** 30. **d-d-d-d-d-d**... **Source:** - Sarcone's **"ding-bong numbers"** are sequence A102701 in the 'Encyclopedia of integer sequences'. - **"Fongaponga"**, Focus BrainTrainer nr. 7, page 51. A five-sided polygon (pentagon) has 5 diagonals. This is the only shape for which the number of sides and diagonals is the same (which may explain why _pentagrams_, _pentacles_, and _pentangles_ are so common and appear so often as iconographic symbols). - by Patrick Vennebush - _Pentagram_, _Pentangle_ and _Pentacle_ are all names for a 5-pointed star. This mystical symbol is supposed to keep away devils and witches.  _Early Greek coin marked with **Quincunx** Pattern_ The number 5 is geometrically represented in the _Quincunx_ pattern. This design is arranged by marking four corners of an imaginary quadrilateral and a central axis through a series of dots or objects - as noticed on dice, playing cards, or dominoes. The significance of the quincunx pattern originates in Pythagorean mathematical mysticism. A famous riddle involving 5s: How can you make the following equation true by drawing only one straight line: 5+5+5=550 Answer: 545+5=550 Another famous riddle: From a word of **5 letters**, take 2 letters and have 1. Answer: ALONE - AL = ONE. • What English word contains all **5** vowels ONCE? Answer: auctioned, authorize, dialogue, discourage, education, housemaid, mensuration, obnubilate, pneumonia, precarious, precaution, regulation, sequoia, tambourine, ultraviolet, uncopyrightable... The words ABSTEMIOUS, ANEMIOUS, ARSENIOUS, CAESIOUS and FACETIOUS contain all 5 vowels appearing in alphabetical order, while in the words SUBCONTINENTAL and UNORIENTAL they appear in reverse alphabetical order! -- _G. Sarcone_. • What Italian/French/Spanish word uses all **5** vowels once? Answer: aiuole (flowerbeds) / oiseau (bird) / murciélago (bat). A list of words that contain all 5 vowels once BOTH in Italian and in Spanish: ADULTERIO, AURIFERO, CAULIFORME, COMUNICANTE, DEPURATIVO, DELUSORIA, EDUCATIVO, EQUIVOCA, ESTUARIO, EUFORIA, FERRUGINOSA, INCESTUOSA, LUTERANISMO, PAUPERISMO, PERUVIANO, SURREALISMO, VITUPEROSA, VOLUMETRIA... -- _G. Sarcone_. In French, some verbs like 'vouaient' (were dedicating, dedicated), 'jouaient' (were playing, played)... contain 5 different consecutive vowels! • "In this exclamation, there are five **_i_**'s!" (autoreferential sentence) 1000 + **5** = 1005 (one thousand five) is the smallest natural number whose name contains the five vowels a, e, i, o, u (in any order). In French "je te dis un mot de cinq lettres!" (I tell you a word of five letters) is an exclamation of anger against the person for whom the insult is intended. **5th April** At 1:02 AM and 3 seconds on Wednesday, April 5, 2006, it was the 1st hour of the day, the 2nd minute of the hour, the 3rd second of that minute in the 4th month and the 5th day of '06... or just: **01**:**02**:**03** **04**-**05**-**06** for short! For many other places, this coincidental chronological oddity happens at 1:02 AM May 4. The five rivers of Hades are: • _**Acheron**_ (the river of woe. Etymologically, the name probably means 'marsh-like': cf. Greek word _akherousai_, 'marshlike water'), • _**Cocytus**_ (the river of lamentation; from Greek _kokutos_, 'lamentation'), • _**Phlegethon**_ (the river of fire; from Greek present participle of _phlegethein_, 'to blaze'), • _**Lethe**_ (the river of forgetfulness; from Greek _lethe_, 'forgetfulness') • _**Styx**_ (the river of hate; cognate with Greek words _stygos_ 'hatred' and _stygnos_ 'gloomy'). Five is a very popular number in Chinese culture since it occupies the central position (one through nine) and also reflects the 'Five Elements Philosophy' (Wuxing) - Wood, Fire, Earth, Metal (or Gold), and Water (in Chinese: 木, mù; 火, huǒ; 土, tǔ; 金, jīn; 水, shǔi). In Switerland, the banking sector employs about **5**% of the workforce (data: 2005). According to a research by Commtouch, quoted by NYT, only 5 countries: China, South Korea, Russia, USA and Brazil generate 99% of spams. The name _Pontius (Pilatus)_, in early Italic language means 'the 5th'. We can find the Indo-european root _penkwro_, the '5th', in the word **finger** (finger, from Germanic _fingwraz_,"one of five"). - by Gianni A. Sarcone - _Macuilxochitl_ was the god and patron of art, games, beauty, dance, flowers, and song in Aztec mythology. His name contains the Nahuatl words _xochitl_ ("flower") and _macuil_ (five), and hence means "Five-flower" (but he could also be referred to as _Chicomexochitl_, "Seven-flower"). The number 5 (**๕**) is pronounced as 'Ha' in Thai language. 555 is also used by some as slang for 'HaHaHa'! **Soup 5**, variously spelled 'Soup Number Five' or 'Soup #5', is a soup made from bull's testicles or penis.The dish originates from Filipino cuisine. It is believed to have strong aphrodisiac properties. **Joke** For those who know German: - Mr. Freud, what is between fear and sex? - F�nf!
_Early Greek coin marked with **Quincunx** Pattern_ The number 5 is geometrically represented in the _Quincunx_ pattern. This design is arranged by marking four corners of an imaginary quadrilateral and a central axis through a series of dots or objects - as noticed on dice, playing cards, or dominoes. The significance of the quincunx pattern originates in Pythagorean mathematical mysticism. A famous riddle involving 5s: How can you make the following equation true by drawing only one straight line: 5+5+5=550 Answer: 545+5=550 Another famous riddle: From a word of **5 letters**, take 2 letters and have 1. Answer: ALONE - AL = ONE. • What English word contains all **5** vowels ONCE? Answer: auctioned, authorize, dialogue, discourage, education, housemaid, mensuration, obnubilate, pneumonia, precarious, precaution, regulation, sequoia, tambourine, ultraviolet, uncopyrightable... The words ABSTEMIOUS, ANEMIOUS, ARSENIOUS, CAESIOUS and FACETIOUS contain all 5 vowels appearing in alphabetical order, while in the words SUBCONTINENTAL and UNORIENTAL they appear in reverse alphabetical order! -- _G. Sarcone_. • What Italian/French/Spanish word uses all **5** vowels once? Answer: aiuole (flowerbeds) / oiseau (bird) / murciélago (bat). A list of words that contain all 5 vowels once BOTH in Italian and in Spanish: ADULTERIO, AURIFERO, CAULIFORME, COMUNICANTE, DEPURATIVO, DELUSORIA, EDUCATIVO, EQUIVOCA, ESTUARIO, EUFORIA, FERRUGINOSA, INCESTUOSA, LUTERANISMO, PAUPERISMO, PERUVIANO, SURREALISMO, VITUPEROSA, VOLUMETRIA... -- _G. Sarcone_. In French, some verbs like 'vouaient' (were dedicating, dedicated), 'jouaient' (were playing, played)... contain 5 different consecutive vowels! • "In this exclamation, there are five **_i_**'s!" (autoreferential sentence) 1000 + **5** = 1005 (one thousand five) is the smallest natural number whose name contains the five vowels a, e, i, o, u (in any order). In French "je te dis un mot de cinq lettres!" (I tell you a word of five letters) is an exclamation of anger against the person for whom the insult is intended. **5th April** At 1:02 AM and 3 seconds on Wednesday, April 5, 2006, it was the 1st hour of the day, the 2nd minute of the hour, the 3rd second of that minute in the 4th month and the 5th day of '06... or just: **01**:**02**:**03** **04**-**05**-**06** for short! For many other places, this coincidental chronological oddity happens at 1:02 AM May 4. The five rivers of Hades are: • _**Acheron**_ (the river of woe. Etymologically, the name probably means 'marsh-like': cf. Greek word _akherousai_, 'marshlike water'), • _**Cocytus**_ (the river of lamentation; from Greek _kokutos_, 'lamentation'), • _**Phlegethon**_ (the river of fire; from Greek present participle of _phlegethein_, 'to blaze'), • _**Lethe**_ (the river of forgetfulness; from Greek _lethe_, 'forgetfulness') • _**Styx**_ (the river of hate; cognate with Greek words _stygos_ 'hatred' and _stygnos_ 'gloomy'). Five is a very popular number in Chinese culture since it occupies the central position (one through nine) and also reflects the 'Five Elements Philosophy' (Wuxing) - Wood, Fire, Earth, Metal (or Gold), and Water (in Chinese: 木, mù; 火, huǒ; 土, tǔ; 金, jīn; 水, shǔi). In Switerland, the banking sector employs about **5**% of the workforce (data: 2005). According to a research by Commtouch, quoted by NYT, only 5 countries: China, South Korea, Russia, USA and Brazil generate 99% of spams. The name _Pontius (Pilatus)_, in early Italic language means 'the 5th'. We can find the Indo-european root _penkwro_, the '5th', in the word **finger** (finger, from Germanic _fingwraz_,"one of five"). - by Gianni A. Sarcone - _Macuilxochitl_ was the god and patron of art, games, beauty, dance, flowers, and song in Aztec mythology. His name contains the Nahuatl words _xochitl_ ("flower") and _macuil_ (five), and hence means "Five-flower" (but he could also be referred to as _Chicomexochitl_, "Seven-flower"). The number 5 (**๕**) is pronounced as 'Ha' in Thai language. 555 is also used by some as slang for 'HaHaHa'! **Soup 5**, variously spelled 'Soup Number Five' or 'Soup #5', is a soup made from bull's testicles or penis.The dish originates from Filipino cuisine. It is believed to have strong aphrodisiac properties. **Joke** For those who know German: - Mr. Freud, what is between fear and sex? - F�nf!  **FIVE** in different languages (© G. Sarcone) (from Old English _**fîf**_) Indo-european | * **PENKWE** | Sanskrit | **
**FIVE** in different languages (© G. Sarcone) (from Old English _**fîf**_) Indo-european | * **PENKWE** | Sanskrit | ** PAÑCA** | Greek, Attic | **ΠENTE** **_PENTE_** | Latin | **QVINQVE** | , Archaic Latin | * **PENQVE** | Vulgar Latin | * **CINQUE** | Italian _**cinque**_; French _**cinq**_; Spanish and Portuguese _**cinco**_; Provençal and Catalan _**cinc**_; Romanian _**cinci**_; Romansh _**tschintg**_; Sardinian _**chímbi**_. Old Celtic | **PEMPE** | Breton _**pemp**_; Welsh **_pump_**; Irish **_cúig_** (things), _**ciúigear**_ (persons). Old Germanic | **FIMFI** | Dutch _vijf_; German _**fünf**_; Danish, Norwegian, and Swedish _**fem**_; Icelandic **_fimm_**. Old Slavic | **PEnTI** | Russian пять _**p'jat'**_; Czech _**pět**_; Slovenian **_pét_**; Polish _**pięć**_. Proto Indo-Iranian | ***PANK'A** | Persian پنج **_panj_**; Hindi पाँच **_panch_**.
PAÑCA** | Greek, Attic | **ΠENTE** **_PENTE_** | Latin | **QVINQVE** | , Archaic Latin | * **PENQVE** | Vulgar Latin | * **CINQUE** | Italian _**cinque**_; French _**cinq**_; Spanish and Portuguese _**cinco**_; Provençal and Catalan _**cinc**_; Romanian _**cinci**_; Romansh _**tschintg**_; Sardinian _**chímbi**_. Old Celtic | **PEMPE** | Breton _**pemp**_; Welsh **_pump_**; Irish **_cúig_** (things), _**ciúigear**_ (persons). Old Germanic | **FIMFI** | Dutch _vijf_; German _**fünf**_; Danish, Norwegian, and Swedish _**fem**_; Icelandic **_fimm_**. Old Slavic | **PEnTI** | Russian пять _**p'jat'**_; Czech _**pět**_; Slovenian **_pét_**; Polish _**pięć**_. Proto Indo-Iranian | ***PANK'A** | Persian پنج **_panj_**; Hindi पाँच **_panch_**.  Evolution from 'seal script' to modern sinograph 五 : Old Chinese (pron.) | **nguo** | Chinese 五 _**wǔ**._ Proto-Semitic | * **KhAMSh** | Semitic root | **Kh-M-Sh** | Ancient Egyptian [dỉ'-] _**t'uau**_; Akkadian _
Evolution from 'seal script' to modern sinograph 五 : Old Chinese (pron.) | **nguo** | Chinese 五 _**wǔ**._ Proto-Semitic | * **KhAMSh** | Semitic root | **Kh-M-Sh** | Ancient Egyptian [dỉ'-] _**t'uau**_; Akkadian _ _ _**khamish**_; Punic _
_ _**khamish**_; Punic _ **khamsh**_. Arabic خمسة _**khamsâ**_; Hebrew חמשה _**khamishah**_; Maltese: _**hamsa**_; Amharic _**amist**_ (pron. amst). More languagesMagyar _**öt**_. Turkish _**bes¸**_. Mayan **_ho_**. Nahuatl _**mācuīlli**_. Suomi **_viisi_**. Zulu **_(isi)hlanu_**. HIDDEN ROOTSThe roots of the word **five** are hidden in the following words: cinquain, Cinquecento, cinquefoil, keno, pachisi, Pentecost, pentesmon, pentagon, pentameter, pentathlon, pinkster flower, Pontius, punch, Quentin, quincunx, quinial, quintain, quintessence, quintet, quintuple; femto-, fin, finger, fist, foist; khamsin. In French: esquinter, quinquagénaire. In Spanish: quintar. In German: Pfinztag, Quentchen. | | | | | | | | | | | | |
| **6 ⠼⠋
**khamsh**_. Arabic خمسة _**khamsâ**_; Hebrew חמשה _**khamishah**_; Maltese: _**hamsa**_; Amharic _**amist**_ (pron. amst). More languagesMagyar _**öt**_. Turkish _**bes¸**_. Mayan **_ho_**. Nahuatl _**mācuīlli**_. Suomi **_viisi_**. Zulu **_(isi)hlanu_**. HIDDEN ROOTSThe roots of the word **five** are hidden in the following words: cinquain, Cinquecento, cinquefoil, keno, pachisi, Pentecost, pentesmon, pentagon, pentameter, pentathlon, pinkster flower, Pontius, punch, Quentin, quincunx, quinial, quintain, quintessence, quintet, quintuple; femto-, fin, finger, fist, foist; khamsin. In French: esquinter, quinquagénaire. In Spanish: quintar. In German: Pfinztag, Quentchen. | | | | | | | | | | | | |
| **6 ⠼⠋  ** | is a congruent number because it is the area of a 3, 4, 5 triangle (a congruent number is an integer that is the area of a right triangle with three rational number sides). is the smallest perfect number, that is a number whose divisors add up to itself, e.g.: 1 x 2 x 3 = 1 + 2 + 3 = 6 The probability that a number picked at random from the set of integers will have no repeated prime divisors is **6/**
** | is a congruent number because it is the area of a 3, 4, 5 triangle (a congruent number is an integer that is the area of a right triangle with three rational number sides). is the smallest perfect number, that is a number whose divisors add up to itself, e.g.: 1 x 2 x 3 = 1 + 2 + 3 = 6 The probability that a number picked at random from the set of integers will have no repeated prime divisors is **6/** 2. - Source: Chartres _n_3 - _n_ is divisible by 6. That is, any product of 3 consecutive integers is divisible by 6. The equation x_n_ - y_m_ = ±**6** with _n_, _m_ > 1 has NO solution. In other words, 6 cannot be a difference of two powers! = 3(1/1 + 1/2 + 1/3 + 1/6) = 62(1/1 - 1/2 - 1/3) = 1/20 + 3/21 + 5/22 + 7/23 + 9/24 + 11/25 + 13/26 + ... (sum of consecutive odd numbers with reciprocal powers of 2) = 4! / 22 = 4! / 2!2 = (
2. - Source: Chartres _n_3 - _n_ is divisible by 6. That is, any product of 3 consecutive integers is divisible by 6. The equation x_n_ - y_m_ = ±**6** with _n_, _m_ > 1 has NO solution. In other words, 6 cannot be a difference of two powers! = 3(1/1 + 1/2 + 1/3 + 1/6) = 62(1/1 - 1/2 - 1/3) = 1/20 + 3/21 + 5/22 + 7/23 + 9/24 + 11/25 + 13/26 + ... (sum of consecutive odd numbers with reciprocal powers of 2) = 4! / 22 = 4! / 2!2 = ( (10 - 10/10))! = (
(10 - 10/10))! = ( (1 +
(1 +  -3) +
-3) +  (1 -
(1 -  -3))2 = (Log(10 x 10 x 10))! = 102 + 102 + 102 = 1102 = DC/C 62 = 36** 62 = 13 + 23 + 33 63 = 33 + 43 + 53 A Simple Mnemonic Math Trick When you multiply 6 by an even number, they both end in the same digit. Example: 6x2=12, 6x4=24, 6x6=36, 6x8=48, etc. 6 is the smallest number of colors needed to color the regions on a map on a Möbius strip. A Möbius strip is a continuous closed surface with only one side; formed from a rectangular strip by rotating one end 180 degrees and joining it with the other end. 6 circles of the same size (try this with 6 coins of the same denomination) will always perfectly surround, all touching, without gaps, 1 circle of that same size. - Posted by Aaron Pyle The probability to get one 6 with 6 dice is 0.665... The probability to get two 6's with 2 x 6 = 12 dice is 0.619... The probability to get three 6's with 3 x 6 = 18 dice is 0.597... Arithmetical nut with 6: "From six take nine; from nine take ten; from forty take fifty, and have six left" (see below) SIX IX IX X XL L S I X A base-6 (senary or heximal) numeral system is used by the Ndom people of the Frederik Hendrik Island, near New Guinea. For example, in Ndom language the number 7 is mer abo sas (6 + 1), and the number 17, mer an thef abo meregh (6 x 2 + 5). "This exclamation has unexpectedly six 's', six 'i' and six 'x'!" (autoreferential sentence) - G. Sarcone. Any one of us is only about 6 acquaintances away from anyone else in the world. Brazilians have two different names for six: seis or meia (short for meia duzia, 'half dozen'). In old French, the word 'hasart' meant 6 at the game of dice. The earliest meaning of HAZARD (<hasart) was, however, 'stroke of luck (or bad luck)'. In the past, the dice featured on one face a flower pattern. Thus the Arabs called gaming dice "flowers", in Arabic 'az-zahr'. the "sixth sick sheik's sixth sheep's sick" is said to be the hardest tongue twister in English. Riddle: can you transform the Roman number IX into 6 by drawing only one line? Answer: SIX (yes, the line is curvilinear...). Joke. Solving the equation by one dumbo:
-3))2 = (Log(10 x 10 x 10))! = 102 + 102 + 102 = 1102 = DC/C 62 = 36** 62 = 13 + 23 + 33 63 = 33 + 43 + 53 A Simple Mnemonic Math Trick When you multiply 6 by an even number, they both end in the same digit. Example: 6x2=12, 6x4=24, 6x6=36, 6x8=48, etc. 6 is the smallest number of colors needed to color the regions on a map on a Möbius strip. A Möbius strip is a continuous closed surface with only one side; formed from a rectangular strip by rotating one end 180 degrees and joining it with the other end. 6 circles of the same size (try this with 6 coins of the same denomination) will always perfectly surround, all touching, without gaps, 1 circle of that same size. - Posted by Aaron Pyle The probability to get one 6 with 6 dice is 0.665... The probability to get two 6's with 2 x 6 = 12 dice is 0.619... The probability to get three 6's with 3 x 6 = 18 dice is 0.597... Arithmetical nut with 6: "From six take nine; from nine take ten; from forty take fifty, and have six left" (see below) SIX IX IX X XL L S I X A base-6 (senary or heximal) numeral system is used by the Ndom people of the Frederik Hendrik Island, near New Guinea. For example, in Ndom language the number 7 is mer abo sas (6 + 1), and the number 17, mer an thef abo meregh (6 x 2 + 5). "This exclamation has unexpectedly six 's', six 'i' and six 'x'!" (autoreferential sentence) - G. Sarcone. Any one of us is only about 6 acquaintances away from anyone else in the world. Brazilians have two different names for six: seis or meia (short for meia duzia, 'half dozen'). In old French, the word 'hasart' meant 6 at the game of dice. The earliest meaning of HAZARD (<hasart) was, however, 'stroke of luck (or bad luck)'. In the past, the dice featured on one face a flower pattern. Thus the Arabs called gaming dice "flowers", in Arabic 'az-zahr'. the "sixth sick sheik's sixth sheep's sick" is said to be the hardest tongue twister in English. Riddle: can you transform the Roman number IX into 6 by drawing only one line? Answer: SIX (yes, the line is curvilinear...). Joke. Solving the equation by one dumbo:  Chinese people like the number 6. One possible reason is because it is the largest number on a dice, and when gambling, one wins if the number six is thrown. When playing mah-jong, the host is the most likely to be the one who throws the number six, and who therefore has a better chance of winning. Reflecting this, the Chinese have a saying, "double six makes you the happiest". For Chinese businessmen the number six means "a smooth business". "Liùhe" (六和), in the Mystical Numbers of Taoism, represents the number 6 and symbolizes the Six Harmonies: 體 合 於 心 (Body in harmony with Heart), 心 合 於 意 (Heart in harmony with Intent), 意 合 於 氣 (Intent in harmony with Qi), 氣 合 於 神 (Qi in harmony with Spirit), 神 合 於 動 (Spirit in harmony with Motion), 動 合 於 空 (Motion in harmony with Nothing). When a Yoruban man in Nigeria get really attracted to a woman, he sends six shells to her. In fact, the Yoruban word efa means both 'six' and 'attracted'. If this chat up line works, the girl replies with eight shells - ejo meaning both 'eight' and 'I agree'! 6 persons Whenever two people meet, there are really six people present. There is each man as he sees himself, each man as the other person sees him, and each man as he really is. -- William James. Italian natural ambigram 9 , 111 111 = 6 un-o dop-o un 9 (this Italian sentence means "6 ones after a 9" and can be read the same upside down).
Chinese people like the number 6. One possible reason is because it is the largest number on a dice, and when gambling, one wins if the number six is thrown. When playing mah-jong, the host is the most likely to be the one who throws the number six, and who therefore has a better chance of winning. Reflecting this, the Chinese have a saying, "double six makes you the happiest". For Chinese businessmen the number six means "a smooth business". "Liùhe" (六和), in the Mystical Numbers of Taoism, represents the number 6 and symbolizes the Six Harmonies: 體 合 於 心 (Body in harmony with Heart), 心 合 於 意 (Heart in harmony with Intent), 意 合 於 氣 (Intent in harmony with Qi), 氣 合 於 神 (Qi in harmony with Spirit), 神 合 於 動 (Spirit in harmony with Motion), 動 合 於 空 (Motion in harmony with Nothing). When a Yoruban man in Nigeria get really attracted to a woman, he sends six shells to her. In fact, the Yoruban word efa means both 'six' and 'attracted'. If this chat up line works, the girl replies with eight shells - ejo meaning both 'eight' and 'I agree'! 6 persons Whenever two people meet, there are really six people present. There is each man as he sees himself, each man as the other person sees him, and each man as he really is. -- William James. Italian natural ambigram 9 , 111 111 = 6 un-o dop-o un 9 (this Italian sentence means "6 ones after a 9" and can be read the same upside down).  6 Photo Snuff is an Indian tobacco brand. • English words which contain strings of 6 consonants: "bergschrund", "borschts", "eschscholtzia", "latchstring", "weltschmerz". 6 x 105 is the number of engineers China produced in 2005. In comparison, India produces nearly 5 x 105 technical graduates annually! (data 2008) SIX in different languages (© G. Sarcone) (Old English siex) Indo-european | * SEKS | | * SWEKS | Sanskrit |
6 Photo Snuff is an Indian tobacco brand. • English words which contain strings of 6 consonants: "bergschrund", "borschts", "eschscholtzia", "latchstring", "weltschmerz". 6 x 105 is the number of engineers China produced in 2005. In comparison, India produces nearly 5 x 105 technical graduates annually! (data 2008) SIX in different languages (© G. Sarcone) (Old English siex) Indo-european | * SEKS | | * SWEKS | Sanskrit |  S'AS' | Greek, Attic | 'EΞ HEX | Latin | SEX | Italian sei; French six; Spanish and Portuguese seis; Provençal sièis; Catalan and Romansh sis; Romanian şase; Sardinian ses. Old Celtic | SUEK(O)S | , | SVEK(O)S | Breton c’hwec’h; Welsh chwech; Irish sé (things), seisear (persons). Old Germanic | SEKS | Dutch zes; German sechs; Danish and Norwegian seks; Swedish and Icelandic sex. Old Slavic | ShESTI | Russian шесть shest'; Czech šest; Slovenian šést; Polish sześć. Proto Indo-Iranian | *(K)SWACSH | Persian شش shesh; Hindi छः ch'eh.
S'AS' | Greek, Attic | 'EΞ HEX | Latin | SEX | Italian sei; French six; Spanish and Portuguese seis; Provençal sièis; Catalan and Romansh sis; Romanian şase; Sardinian ses. Old Celtic | SUEK(O)S | , | SVEK(O)S | Breton c’hwec’h; Welsh chwech; Irish sé (things), seisear (persons). Old Germanic | SEKS | Dutch zes; German sechs; Danish and Norwegian seks; Swedish and Icelandic sex. Old Slavic | ShESTI | Russian шесть shest'; Czech šest; Slovenian šést; Polish sześć. Proto Indo-Iranian | *(K)SWACSH | Persian شش shesh; Hindi छः ch'eh.  Evolution from 'seal script' to modern sinograph 六 : Old Chinese (pron.) | lyuk | Chinese 六 liù. Proto-Semitic | * ShIDTh | Semitic root | Sh-Sh | , | Sh-T | Ancient Egyptian [sỉs'- or ỉs'- (?)] sas; Akkadian
Evolution from 'seal script' to modern sinograph 六 : Old Chinese (pron.) | lyuk | Chinese 六 liù. Proto-Semitic | * ShIDTh | Semitic root | Sh-Sh | , | Sh-T | Ancient Egyptian [sỉs'- or ỉs'- (?)] sas; Akkadian  shishshu; Punic
shishshu; Punic  shish. Arabic ستة sittâ; Hebrew ששה shishah; Maltese: sitta; Amharic sidist (pron. sədəsətə). More languagesMagyar hat. Turkish altı. Mayan uac. Nahuatl chicuacē. Suomi kuusi. Zulu isithupha. HIDDEN ROOTSThe roots of the word six are hidden in the following words: bisextil, hexad, hexagon, Seicento, semester, senary, sestet, sestina, sext, sextant, sextile, sextuple, siesta, Sistine. In French: setier, sexagénaire, sextuor, sizain. In Italian: sciamito [< Greek _(he)xámiton_], seienne, staio. | | | | | | | | | | |
shish. Arabic ستة sittâ; Hebrew ששה shishah; Maltese: sitta; Amharic sidist (pron. sədəsətə). More languagesMagyar hat. Turkish altı. Mayan uac. Nahuatl chicuacē. Suomi kuusi. Zulu isithupha. HIDDEN ROOTSThe roots of the word six are hidden in the following words: bisextil, hexad, hexagon, Seicento, semester, senary, sestet, sestina, sext, sextant, sextile, sextuple, siesta, Sistine. In French: setier, sexagénaire, sextuor, sizain. In Italian: sciamito [< Greek _(he)xámiton_], seienne, staio. | | | | | | | | | | |
 0-6 |
0-6 |  7-12 |
7-12 | 13-23 |
13-23 |  24-69 |
24-69 |  70-200 |
70-200 |  201-∞ |
201-∞ |  5H0P
5H0P
You're encouraged to expand and/or improve the number facts featured on this page. Send us your comments, feedback or suggestions.
You can use any of our content (pictures, texts) in your non-commercial web page for free as long as you leave the copyright and author's info intact and link to us.
 This work is licensed under a Creative Commons Attribution - NonCommercial - ShareAlike 2.5 License.
This work is licensed under a Creative Commons Attribution - NonCommercial - ShareAlike 2.5 License.
Source credits 1. We always credit our sources, when we can. 2. Some of the material on this web section is submitted by our readers/visitors. Where cited, excerpts are quoted or italicized, and authorship credit is prominently supplied. 3. Most authors/submitters, however, prefer to remain anonymous, for reasons of their own, and we respect their wishes. 4. If you believe you have identified material on this web site that has not proper permission (and can provide us with verifiable proof of ownership), or that should (but does not) credit a verifiable source, please bring it to our attention. 5. Any oversights, omissions and corrections will be updated as soon as possible.
Encyclopedia of Numbers © G. Sarcone, Archimedes Lab, Genoa, Italy