Semiconductor laser Diodes, Edge-emitting lasers, Fabry-Perot Lasers (original) (raw)
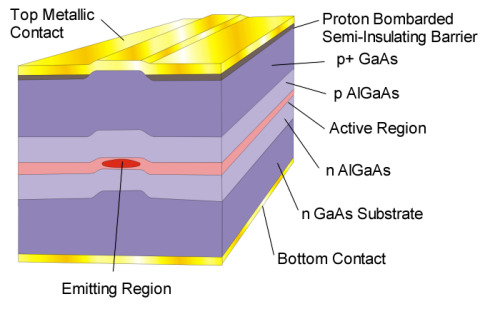
Figure 1 . Schematic diagram of a Fabry-Perot laser.
Figure 1. Shows the structure of a typical edge-emitting laser. The dimensions of the active region are 200 m m in length, 2-10 m m lateral width and 0.1 m m in transverse dimension. In reality there are many different designs ofedge-emitting lasers. Current flows from the p to the type semiconductor with electrons and holes being injected in the active region. A further advantage of the double heterostructure is that the large bandgap semiconductor has a lower refractive index than that in the active region giving index guiding in the transverse direction. In the plain of the active region the emission is confined by gain guiding, where the refractive index is modified by the carrier density. The formation of a stripe contact separated by a semi-insulating regions of proton bombarded semiconductor allows the current to flow through a restricted portion of the active region. This also aid the optical confinement in the plane of the active region.
We have seen in the last section that p-n junctions can be used to create a laser. The current required to achieve lasing is enormous. This is because there is in defined region for radiative recombination to occur. Electrons and hole can just drift through the junction without recombining. A more efficient solution is to use heterostructures and double heterostructures.
A heterostructure, as the name suggests uses to different types of semiconductor with one with a larger bandgap than the other. When the two semiconductors are brought together potential barriers are formed which can confine the electrons and holes. The situation is further improved in the double heterostructure.
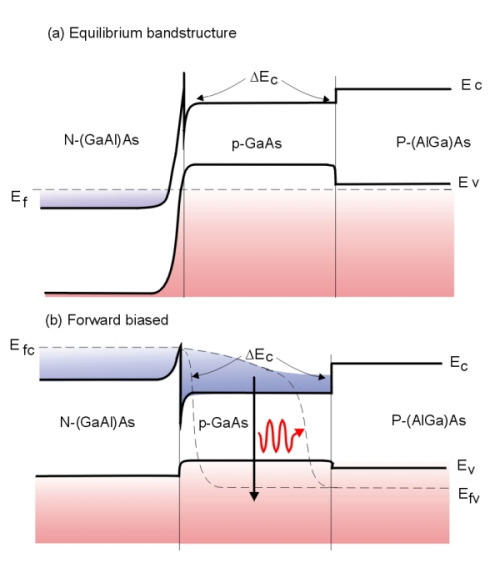
Figure 2 . Bandedge diagram of a NpP AlGaAs/GaAs/AlGaAs heterostructure.
Figure 2. a) shows a NpP double heterostructure, (the capital letters represent the larger bandgap semiconductors). In this case for AlGaAs/GaAs/AlGaAs in equilibrium. The Fermi level is constant across the junction and causes the band profile to bend as shown.
In Figure 2. b), the double heterostructure has been forward biased causing an injection of electrons and holes into the device, the depletion region is reduced and the bands of the N-type AlGaAs shift upwards. When the voltage is sufficient, the quasi-Fermi level for the N-type material is at the same energy and the electrons can overcome the potential barrier D E c and flow into the p-GaAs region where they are confined by the lower bandgap material. Similarly, holes flow in from the P-type AlGaAs to the p-GaAs valence band. The electrons and holes are confined where they can combine radiatively.
Population inversion is not enough to create a laser. In order for stimulated emission to become significant, the light must interact with the electrons in the conduction band. This is achieved by creating a resonant cavity in which the light is reflected back and forth many times before leaving the cavity. If the gain equals loss, lasing will occur.
We can analyses qualitatively analyse the loss processes and calculate the minimum gain as well as the resonant cavity conditions.
The design of the cavity structures for modern heterostructure lasers can be much more complicated incorporating more than one set of cladding layers to confine the carriers (Separate Confinement Heterostructure SCH) or GRaded-INdex Separate Confinement Heterostructures (GRINSCH). Quantum well and Multiple Quantum Well (MQW) active regions have superseded bulk active-regions because of the advantages that they offer. A quantum well is formed when the width of the active region of the laser becomes comparable with the De-Broglie wavelength, (approx. 100 Å). In this situation, the electron states are no longer quasi-continuous but become separated until only a few states lie within the well. The width of the well determines the number and separation of the energy levels within the well, thus the allowed energy transitions. Radiative recombination in the quantum well is predominantly from the first energy level in the conduction band to the first energy level in the heavy-hole valence band. Therefore, the separation of the energy levels can be tailored by careful design of the well width. Another advantage of quantum well lasers is that the temperature dependence of the intrinsic threshold current (i.e. only including properties that are intrinsic to the gain medium.) is linear with temperature. [] Well designed quantum well lasers have low threshold currents and are very reliable with estimated lifetimes of greater than 10 6 hours.
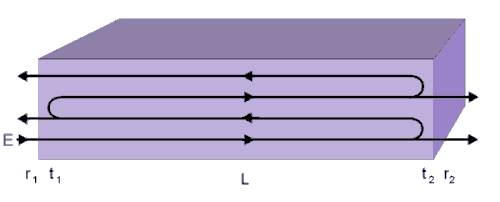
Figure 3. Wave propagation through the semiconductor cavity. An incident wave of amplitude is partially transmitted with ratio t 1 and the right hand facet of the cavity the amplitude has attenuated exponentially and this amplitude is transmitted with ratio t 2 . Subsequent reflections from the ends of the cavity are summed at the right hand facet from which the threshold conditions can be calculated.
Consider a semiconductor laser cavity of length L with a plane wave with complex propagation constant
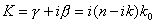
and amplitude E incident on the left hand side of the cavity. The ratio of transmitted to incident light is t 1 and the ratio of transmitted to incident fields at the left is taken as t 2 . The ratio of reflected to incident fields with the optical cavity is r 1 exp( i q 1 ) at the left-hand mirror and r 2 exp( i q 2 ) at the right-hand mirror. For a low loss medium, the phase shifts q 1 and q 2 are small and are generally neglected.
Without time dependence, the plane wave electric field is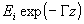 such that E x is t i E i at the first transmition boundary t 1 E i exp( - K L ) just inside the right boundary. The first portion of the field transmitted at the right boundary is t 1 t 2 E i exp( - K L ). The next portion of the wave transmitted is at the right boundary becomes t 1 t 2 r 1 r 2 E i exp( -3 K L ) and so on. Addition of these transmitted fields gives:
such that E x is t i E i at the first transmition boundary t 1 E i exp( - K L ) just inside the right boundary. The first portion of the field transmitted at the right boundary is t 1 t 2 E i exp( - K L ). The next portion of the wave transmitted is at the right boundary becomes t 1 t 2 r 1 r 2 E i exp( -3 K L ) and so on. Addition of these transmitted fields gives:
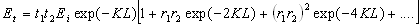
The sum is a geometric progression which permits the last equation to be written as
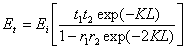
When the denominator of the last equation tends to zero, the condition of a finite transmitted wave E t with zero E i is obtained, which is the condition for oscillation. Therefore the oscillation condition is reached when
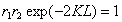
The substituting the term for K defined above and remembering that k 0 =2 p / l 0 and also k = a l 0 /4 p into the resonance condition we obtain:
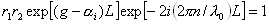
The absorption term has been written as the difference between the gain and the losses a i . The condition for oscillation represents a wave making a round trip of 2L inside the cavity to the starting plane with the same amplitude and phase, within a multiple of 2 p . The amplitude condition is:
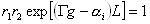
This more usually written,
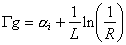
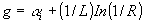
where R = R 1 = r 1 r 1 * = R 2 = r 2 r 2 * is the power reflectivity. For cleaved semiconductor facets in GaAs R~0.3. An additional factor which is often included is the optical confinement factor G which measures the ratio of the emission mode within the active region. For bulk edge emitting lasers this is close to unity but for quantum well lasers it is considerably smaller (about 0.1).
The phase condition becomes:
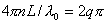
which reduces to
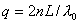
A resonance occurs when an integer number of half-wavelength l 0 will fit into the cavity.
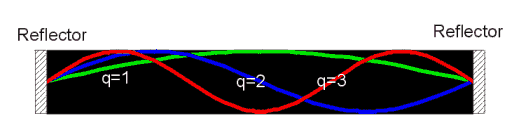
Figure 4. Schematic laser cavity showing the first three modes.
For example in a GaAs cavity of 200 m m in length there will be around 1600 modes. The longitudinal mode separation is given by differentiating
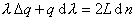 (2)
(2)
For adjacent modes, q=-1 and the substituting equation (1).
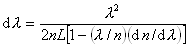 (3)
(3)
To a first approximation, d n /d l is small therefore
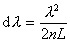 (4)
(4)
with L>> l the mode spacing is rather small and many modes will fit into the cavity of the laser. The diagram shows the emission spectra of an edge emitting laser just below threshold. The closely space modes are superimposed on the spontaneous emission profile. As the current is increased to just above threshold one lasing mode becomes dominant.
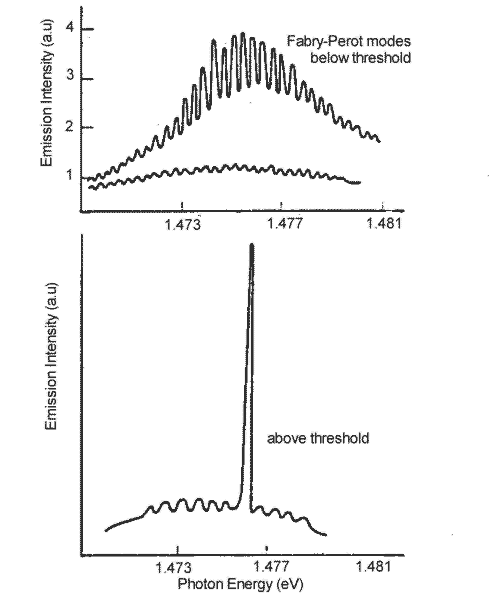
Figure 5. Emission spectra of an edge-emitting laser below threshold and above.
Since the spontaneous emission spectrum is rather broad, several modes compete to become the dominant lasing mode and this mode can switch or mode hop while operating. This characteristic is most undesirable in lasers for telecommunications.