Jonathan Shewchuk's papers (original) (raw)
Surveys and Expository Papers
FAR AND AWAY MY MOST POPULAR PAPER is my introduction to the conjugate gradient method.I have also written a (draft) survey article on spectral and isoperimetric graph partitioning, a survey article on mesh generation, and lecture notes for Berkeley's introductory class on machine learning.
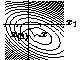 An Introduction to the Conjugate Gradient Method Without the Agonizing Pain, August 1994. Abstract, PostScript (1,716k, 58 pages), PDF (516k, 58 pages), PostScript of classroom figures (1,409k, 37 pages). PDF of classroom figures (394k, 37 pages). This report is an exercise in trying to make a difficult subject as transparent and easy to understand as humanly possible. It includes sixty-six illustrations and as much intuition as I can provide. How could fifteen lines of pseudocode take fifty pages to explain?
An Introduction to the Conjugate Gradient Method Without the Agonizing Pain, August 1994. Abstract, PostScript (1,716k, 58 pages), PDF (516k, 58 pages), PostScript of classroom figures (1,409k, 37 pages). PDF of classroom figures (394k, 37 pages). This report is an exercise in trying to make a difficult subject as transparent and easy to understand as humanly possible. It includes sixty-six illustrations and as much intuition as I can provide. How could fifteen lines of pseudocode take fifty pages to explain?- Concise Machine Learning, unpublished lecture notes, May 2019. PDF (29.6M, 168 pages). My lectures notes for UC Berkeley's classCS 189/289A,Machine Learning, which is both an undergraduate and introductory graduate course. It is concise because not a word is included that cannot be written or spoken in a single semester's lectures and because the choice of topics is limited to a small selection of particularly useful, popular algorithms. Topics include … classification: perceptrons, support vector machines (SVMs), Gaussian discriminant analysis (including linear discriminant analysis, LDA, and quadratic discriminant analysis, QDA), logistic regression, decision trees, neural networks, convolutional neural networks, nearest neighbor search; regression: least-squares linear regression, logistic regression, polynomial regression, ridge regression, Lasso; density estimation: maximum likelihood estimation (MLE); dimensionality reduction: principal components analysis (PCA), random projection, latent factor analysis; and clustering: _k_-means clustering, hierarchical clustering, spectral graph clustering.
- Spectral and Isoperimetric Graph Partitioning, unpublished preprint, 2016. COMMENTS NEEDED! Help me improve this manuscript. If you read this, please send feedback. PDF (567k, 69 pages). An exposition of spectral algorithms for graph partitioning and graph clustering, as well as the closely related isoperimetric graph partitioning algorithm. Additional topics include Cheeger's inequality, the normalized cut criterion, vertex separators, negative edge weights, eigenvector computations, singular value decompositions for bipartite graphs, the use of multiple eigenvectors, and partitioning a graph into more than two subgraphs.
 Unstructured Mesh Generation, chapter 10 ofCombinatorial Scientific Computing (Uwe Naumann and Olaf Schenk, editors), pages 257–297, CRC Press, January 2012. PostScript (1,756k, 41 pages). A survey of the four main method of mesh generation: advancing front methods, Delaunay triangulations, grid and octree methods, and mesh improvement (also known as “clean-up”). My goals for this chapter were to trace the historical origins of many well-known ideas in mesh generation, and to provide a greater level of algorithmic detail than you would expect in a survey this short. Note that this version differs slightly from the version in the book in one respect: I use slightly more verbose references here.
Unstructured Mesh Generation, chapter 10 ofCombinatorial Scientific Computing (Uwe Naumann and Olaf Schenk, editors), pages 257–297, CRC Press, January 2012. PostScript (1,756k, 41 pages). A survey of the four main method of mesh generation: advancing front methods, Delaunay triangulations, grid and octree methods, and mesh improvement (also known as “clean-up”). My goals for this chapter were to trace the historical origins of many well-known ideas in mesh generation, and to provide a greater level of algorithmic detail than you would expect in a survey this short. Note that this version differs slightly from the version in the book in one respect: I use slightly more verbose references here.
Delaunay Mesh Generation
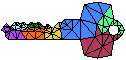 DELAUNAY REFINEMENT MESH GENERATION ALGORITHMSconstruct meshes of triangles or tetrahedra (“elements”) that are suitable for applications like interpolation, rendering, terrain databases, geographic information systems, and most demandingly, the solution of partial differential equations by the finite element method. Delaunay refinement algorithms operate by maintaining a Delaunay or constrained Delaunay triangulation which is refined by inserting additional vertices until the mesh meets constraints on element quality and size. These algorithms simultaneously offer theoretical bounds on element quality, edge lengths, and spatial grading of element sizes; topological and geometric fidelity to complicated domains, including curved domains with internal boundaries; and truly satisfying performance in practice.
DELAUNAY REFINEMENT MESH GENERATION ALGORITHMSconstruct meshes of triangles or tetrahedra (“elements”) that are suitable for applications like interpolation, rendering, terrain databases, geographic information systems, and most demandingly, the solution of partial differential equations by the finite element method. Delaunay refinement algorithms operate by maintaining a Delaunay or constrained Delaunay triangulation which is refined by inserting additional vertices until the mesh meets constraints on element quality and size. These algorithms simultaneously offer theoretical bounds on element quality, edge lengths, and spatial grading of element sizes; topological and geometric fidelity to complicated domains, including curved domains with internal boundaries; and truly satisfying performance in practice.
It gives me great pleasure to announce my first book, co-authored withSiu-Wing Cheng of the Hong Kong University of Science and Technology andTamal Dey of The Ohio State University.
-
 Siu-Wing Cheng, Tamal Krishna Dey, and Jonathan Richard Shewchuk,Delaunay Mesh Generation, xii+375 pages. CRC Press, Boca Raton, Florida, December 2012. Buy it fromTaylor & Francis, fromAmazon, or fromBarnes & Noble.
Siu-Wing Cheng, Tamal Krishna Dey, and Jonathan Richard Shewchuk,Delaunay Mesh Generation, xii+375 pages. CRC Press, Boca Raton, Florida, December 2012. Buy it fromTaylor & Francis, fromAmazon, or fromBarnes & Noble.
Our book is a thorough guide to Delaunay refinement algorithms that are mathematically guaranteed to generate meshes with high quality, including triangular meshes in the plane, tetrahedral volume meshes, and triangular surface meshes embedded in three dimensions. It is also the most complete guide available to Delaunay triangulations and algorithms for constructing them.
This book has its own web page; click here for more details.
The book has fifteen chapters.Check out free samples of theTable of Contents (PDF, 198k, 13 pages),Chapter 1 (PDF, 708k, 30 pages),Chapter 2 (PDF, 286k, 24 pages),Chapter 9 (PDF, 472k, 17 pages), andChapter 13 (PDF, 455k, 29 pages).- 1. Introduction.
- 2. Two-dimensional Delaunay triangulations.
- 3. Algorithms for constructing Delaunay triangulations.
- 4. Three-dimensional Delaunay triangulations.
- 5. Algorithms for constructing Delaunay triangulations in R3.
- 6. Delaunay refinement in the plane.
- 7. Voronoi diagrams and weighted complexes.
- 8. Tetrahedral meshing of PLCs.
- 9. Weighted Delaunay refinement for PLCs with small angles.
- 10. Sliver exudation.
- 11. Refinement for sliver exudation.
- 12. Smooth surfaces and point samples.
- 13. Restricted Delaunay triangulations of surface samples.
- 14. Meshing smooth surfaces and volumes.
- 15. Meshing piecewise smooth complexes. The following papers include theoretical treatments of Delaunay refinement and discussions of the implementation details of my two-dimensional mesh generator and Delaunay triangulator, Triangle, and my three-dimensional mesh generator and Delaunay tetrahedralizer,Pyramid. See the Triangle page for information about what Triangle can do, or to obtain the C source code.
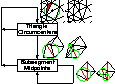 Delaunay Refinement Algorithms for Triangular Mesh Generation, Computational Geometry: Theory and Applications 22(1–3):21–74, May 2002. PostScript (5,128k, 54 pages), PDF (1,046k, 54 pages).Winner of the 2012 Test-of-Time Award from the journal Computational Geometry: Theory and Applications.My ultimate article on two-dimensional Delaunay refinement, including a full theoretical treatment plus extensive pseudocode. This is the first one to read if you want to implement a triangular Delaunay refinement mesh generator, unless you have the book, which is more up to date. (For a discussion of data structures, see the book or Chapter 5 of my dissertation.)
Delaunay Refinement Algorithms for Triangular Mesh Generation, Computational Geometry: Theory and Applications 22(1–3):21–74, May 2002. PostScript (5,128k, 54 pages), PDF (1,046k, 54 pages).Winner of the 2012 Test-of-Time Award from the journal Computational Geometry: Theory and Applications.My ultimate article on two-dimensional Delaunay refinement, including a full theoretical treatment plus extensive pseudocode. This is the first one to read if you want to implement a triangular Delaunay refinement mesh generator, unless you have the book, which is more up to date. (For a discussion of data structures, see the book or Chapter 5 of my dissertation.)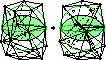 Delaunay Refinement Mesh Generation, Ph.D. thesis, Technical Report CMU-CS-97-137, School of Computer Science, Carnegie Mellon University, Pittsburgh, Pennsylvania, 18 May 1997. Abstract (with BibTeX citation), compressed PostScript (1,768k, 207 pages)(expands to 10,435k when uncompressed), PDF (2,635k, 207 pages). Includes extensive treatment of Delaunay triangulations, two- and three-dimensional Delaunay refinement algorithms, and implementation details. However, Chapter 3 on two-dimensional Delaunay refinement is superseded by the much-improved article above.
Delaunay Refinement Mesh Generation, Ph.D. thesis, Technical Report CMU-CS-97-137, School of Computer Science, Carnegie Mellon University, Pittsburgh, Pennsylvania, 18 May 1997. Abstract (with BibTeX citation), compressed PostScript (1,768k, 207 pages)(expands to 10,435k when uncompressed), PDF (2,635k, 207 pages). Includes extensive treatment of Delaunay triangulations, two- and three-dimensional Delaunay refinement algorithms, and implementation details. However, Chapter 3 on two-dimensional Delaunay refinement is superseded by the much-improved article above. Tetrahedral Mesh Generation by Delaunay Refinement, Proceedings of the Fourteenth Annual Symposium on Computational Geometry (Minneapolis, Minnesota), pages 86–95, Association for Computing Machinery, June 1998. PostScript (1,504k, 10 pages), PDF (299k, 10 pages). A description of the core three-dimensional mesh generation algorithm used in Pyramid, for those who want a quick overview with less detail. A more thorough treatment appears in Chapter 4 of my dissertation.
Tetrahedral Mesh Generation by Delaunay Refinement, Proceedings of the Fourteenth Annual Symposium on Computational Geometry (Minneapolis, Minnesota), pages 86–95, Association for Computing Machinery, June 1998. PostScript (1,504k, 10 pages), PDF (299k, 10 pages). A description of the core three-dimensional mesh generation algorithm used in Pyramid, for those who want a quick overview with less detail. A more thorough treatment appears in Chapter 4 of my dissertation.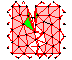 Triangle: Engineering a 2D Quality Mesh Generator and Delaunay Triangulator, in Applied Computational Geometry: Towards Geometric Engineering (Ming C. Lin and Dinesh Manocha, editors), volume 1148 of Lecture Notes in Computer Science, pages 203–222, Springer-Verlag (Berlin), May 1996.From the First Workshop on Applied Computational Geometry (Philadelphia, Pennsylvania). Abstract (with BibTeX citation), PostScript (513k, 10 pages), PDF (153k, 10 pages), HTML. A short paper on Triangle, for those who want a quick overview with less detail. All this material is scattered through my dissertationas well.
Triangle: Engineering a 2D Quality Mesh Generator and Delaunay Triangulator, in Applied Computational Geometry: Towards Geometric Engineering (Ming C. Lin and Dinesh Manocha, editors), volume 1148 of Lecture Notes in Computer Science, pages 203–222, Springer-Verlag (Berlin), May 1996.From the First Workshop on Applied Computational Geometry (Philadelphia, Pennsylvania). Abstract (with BibTeX citation), PostScript (513k, 10 pages), PDF (153k, 10 pages), HTML. A short paper on Triangle, for those who want a quick overview with less detail. All this material is scattered through my dissertationas well. François Labelle and Jonathan Richard Shewchuk,Anisotropic Voronoi Diagrams and Guaranteed-Quality Anisotropic Mesh Generation, Proceedings of the Nineteenth Annual Symposium on Computational Geometry (San Diego, California), pages 191–200, Association for Computing Machinery, June 2003. PostScript (910k, 10 pages), PDF (284k, 10 pages). The best triangulations for interpolation and numerical modeling are often anisotropic: long and skinny, oriented in directions dictated by the function being approximated. (See my “What Is a Good Linear Element?” papers below for details.) The ideal orientations and aspect ratios of the elements may vary greatly from one position to another. This paper discusses a Voronoi refinement algorithm for provably good anisotropic mesh generation. The skewed elements are generated with the help of_anisotropic Voronoi diagrams_, wherein each site has its own distorted distance metric. Anisotropic Voronoi diagrams are somewhat badly behaved, and do not always dualize to triangulations. We call it “Voronoi refinement” because the diagrams can be tamed by inserting new sites. After they are carefully refined, they dualize to guaranteed-quality anisotropic triangular meshes.
François Labelle and Jonathan Richard Shewchuk,Anisotropic Voronoi Diagrams and Guaranteed-Quality Anisotropic Mesh Generation, Proceedings of the Nineteenth Annual Symposium on Computational Geometry (San Diego, California), pages 191–200, Association for Computing Machinery, June 2003. PostScript (910k, 10 pages), PDF (284k, 10 pages). The best triangulations for interpolation and numerical modeling are often anisotropic: long and skinny, oriented in directions dictated by the function being approximated. (See my “What Is a Good Linear Element?” papers below for details.) The ideal orientations and aspect ratios of the elements may vary greatly from one position to another. This paper discusses a Voronoi refinement algorithm for provably good anisotropic mesh generation. The skewed elements are generated with the help of_anisotropic Voronoi diagrams_, wherein each site has its own distorted distance metric. Anisotropic Voronoi diagrams are somewhat badly behaved, and do not always dualize to triangulations. We call it “Voronoi refinement” because the diagrams can be tamed by inserting new sites. After they are carefully refined, they dualize to guaranteed-quality anisotropic triangular meshes.- Talk slides: Anisotropic Voronoi Diagrams and Guaranteed-Quality Anisotropic Mesh Generation. PDF (color, 1,301k, 47 pages). Slides from a talk on our paper above. You can evenwatch me give a shorter version of this talk at the Mathematical Sciences Research Institute.
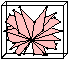 Mesh Generation for Domains with Small Angles, Proceedings of the Sixteenth Annual Symposium on Computational Geometry (Hong Kong), pages 1–10, Association for Computing Machinery, June 2000. PostScript (663k, 10 pages), PDF (237k, 10 pages). How to adapt Delaunay refinement algorithms to domains that are difficult to mesh because they have small angles. The two-dimensional portion of this paper is superseded by the improved writing in “Delaunay Refinement Algorithms for Triangular Mesh Generation,” above. The three-dimensional portion is still found only here.
Mesh Generation for Domains with Small Angles, Proceedings of the Sixteenth Annual Symposium on Computational Geometry (Hong Kong), pages 1–10, Association for Computing Machinery, June 2000. PostScript (663k, 10 pages), PDF (237k, 10 pages). How to adapt Delaunay refinement algorithms to domains that are difficult to mesh because they have small angles. The two-dimensional portion of this paper is superseded by the improved writing in “Delaunay Refinement Algorithms for Triangular Mesh Generation,” above. The three-dimensional portion is still found only here.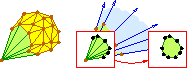 Star Splaying: An Algorithm for Repairing Delaunay Triangulations and Convex Hulls, Proceedings of the Twenty-First Annual Symposium on Computational Geometry (Pisa, Italy), pages 237–246, Association for Computing Machinery, June 2005. PostScript (392k, 10 pages), PDF (209k, 10 pages). Star splaying is a general-dimensional algorithm for fixing broken Delaunay triangulations and convex hulls. Its input is a triangulation, an approximate convex hull, or even just a set of vertices and guesses about who their neighbors are. If the input is “nearly Delaunay” or “nearly convex,” star splaying is quite fast, so I call it a “Delaunay repair” algorithm. Star splaying is designed for dynamic mesh generation, to repair the quality of a finite element mesh that has lost the Delaunay property after its vertices have moved in response to simulated physical forces. Star splaying is akin to Lawson's edge flip algorithm for converting a two-dimensional triangulation to a Delaunay triangulation, but it works in any dimensionality.
Star Splaying: An Algorithm for Repairing Delaunay Triangulations and Convex Hulls, Proceedings of the Twenty-First Annual Symposium on Computational Geometry (Pisa, Italy), pages 237–246, Association for Computing Machinery, June 2005. PostScript (392k, 10 pages), PDF (209k, 10 pages). Star splaying is a general-dimensional algorithm for fixing broken Delaunay triangulations and convex hulls. Its input is a triangulation, an approximate convex hull, or even just a set of vertices and guesses about who their neighbors are. If the input is “nearly Delaunay” or “nearly convex,” star splaying is quite fast, so I call it a “Delaunay repair” algorithm. Star splaying is designed for dynamic mesh generation, to repair the quality of a finite element mesh that has lost the Delaunay property after its vertices have moved in response to simulated physical forces. Star splaying is akin to Lawson's edge flip algorithm for converting a two-dimensional triangulation to a Delaunay triangulation, but it works in any dimensionality.- Kevin Buchin, Olivier Devillers, Wolfgang Mulzer, Okke Schrijvers, and Jonathan Shewchuk,Vertex Deletion for 3D Delaunay Triangulations, 21st Annual European Symposium on Algorithms, volume 8125 of Lecture Notes in Computer Science, pages 253–264, Springer-Verlag (Berlin), September 2013. PDF (400k, 12 pages). A fast randomized algorithm for deleting a vertex from a three-dimensional Delaunay triangulation. Its running time is a bit difficult to explain, but it matches or beats competing algorithms in theory and practice.
- Talk slides: Theoretically Guaranteed Delaunay Mesh Generation—In Practice,September 2005. PDF (color, 2,003k, 106 pages). Slides from a short course I gave at the Thirteenth and Fourteenth International Meshing Roundtables. Not just about my work! This is a survey of what I see as the most central contributions to provably good mesh generation, restricted to algorithms that have been demonstrated to work in practice as well as in theory. It includes full citations for all the featured algorithms, and is designed to be a fast, readable introduction to the area. Topics covered include a short review of Delaunay triangulations and constrained Delaunay triangulations; extensive coverage of Delaunay refinement algorithms for triangular and tetrahedral mesh generation, including methods by Chew, Ruppert, Boivin/Ollivier-Gooch, Miller/Walkington/Pav, Üngör, and me; handling of 2D domains with curved boundaries; handling of 2D and 3D domains with small angles; sliver elimination; and a brief discussion of how to prove that a Delaunay refinement algorithm eliminates bad elements.
Non-Delaunay Mesh Generation, Dynamic Meshing, and Physically-Based Computer Animation
“I hate meshes. I cannot believe how hard this is. Geometry is hard.”
— David Baraff, Senior Research Scientist, Pixar Animation Studios
THE GREAT CHALLENGE OF TETRAHEDRAL MESH GENERATIONis to create tetrahedra whose dihedral angles are never too small nor too large. Although Delaunay refinement usually does this well in practice, there's lots of room for improvement—in obtaining mathematically guaranteed bounds on angles, in further improving the angles beyond what Delaunay algorithms or guaranteed-quality algorithms can provide, and in maintaining the quality as a domain changes shape during a simulation. Our isosurface stuffing algorithm comes with theoretical guarantees on dihedral angles. Through mesh improvement procedures, we can make the tetrahedra even better in practice. We use the same mesh improvement methods as a basis for _dynamic meshing_algorithms for simulating objects undergoing radical changes in shape. We also use a simpler, faster form of dynamic meshing to simulate a surgical procedure in which a steerable needle is inserted into flesh.
 François Labelle and Jonathan Richard Shewchuk,Isosurface Stuffing: Fast Tetrahedral Meshes with Good Dihedral Angles, ACM Transactions on Graphics 26(3):57.1–57.10, August 2007. Special issue on Proceedings of SIGGRAPH 2007. PDF (color, 3,530k, 10 pages). The isosurface stuffing algorithm fills an isosurface with a mesh whose dihedral angles are bounded between 10.7o and 164.8o. We're pretty proud of this, because virtually nobody has been able to prove dihedral angle bounds anywhere close to this, except for very simple geometries. Although the tetrahedra at the isosurface must be uniformly sized, the tetrahedra in the interior can be graded. The algorithm is whip fast, numerically robust, and easy to implement because, like Marching Cubes, it generates tetrahedra from a small set of precomputed stencils. The angle bounds are guaranteed by a computer-assisted proof. If the isosurface is a smooth 2-manifold with bounded curvature, and the tetrahedra are sufficiently small, then the boundary of the mesh is guaranteed to be a geometrically and topologically accurate approximation of the isosurface. Unfortunately, the algorithm rounds off sharp corners and edges. (I think it will be extremely hard for anyone to devise an algorithm that provably obtains dihedral angle bounds of this order _and_conforms perfectly to creases.)
François Labelle and Jonathan Richard Shewchuk,Isosurface Stuffing: Fast Tetrahedral Meshes with Good Dihedral Angles, ACM Transactions on Graphics 26(3):57.1–57.10, August 2007. Special issue on Proceedings of SIGGRAPH 2007. PDF (color, 3,530k, 10 pages). The isosurface stuffing algorithm fills an isosurface with a mesh whose dihedral angles are bounded between 10.7o and 164.8o. We're pretty proud of this, because virtually nobody has been able to prove dihedral angle bounds anywhere close to this, except for very simple geometries. Although the tetrahedra at the isosurface must be uniformly sized, the tetrahedra in the interior can be graded. The algorithm is whip fast, numerically robust, and easy to implement because, like Marching Cubes, it generates tetrahedra from a small set of precomputed stencils. The angle bounds are guaranteed by a computer-assisted proof. If the isosurface is a smooth 2-manifold with bounded curvature, and the tetrahedra are sufficiently small, then the boundary of the mesh is guaranteed to be a geometrically and topologically accurate approximation of the isosurface. Unfortunately, the algorithm rounds off sharp corners and edges. (I think it will be extremely hard for anyone to devise an algorithm that provably obtains dihedral angle bounds of this order _and_conforms perfectly to creases.) Nuttapong Chentanez, Bryan Feldman, François Labelle, James O'Brien, and Jonathan Richard Shewchuk,Liquid Simulation on Lattice-Based Tetrahedral Meshes, 2007 Symposium on Computer Animation (San Diego, California), pages 219–228, August 2007. PDF (color, 4,782k, 10 pages). Here, we use isosurface stuffing (above) as part of an algorithm for simulating liquids with free surfaces. The graded meshes allow us to maintain fine detail on the liquid surface without excessive computational cost in the interior. The rendered surface is represented as a separate surface triangulation, at an even finer detail than the surface of the tetrahedral mesh. We exploit the regularity of the meshes for fast point location, needed for semi-Lagrangian advection of the velocities and the surface itself. We also introduce a thickening strategy to prevent the liquid from breaking up into sheets or droplets so thin that they disappear, falling below the finest resolution of the mesh.
Nuttapong Chentanez, Bryan Feldman, François Labelle, James O'Brien, and Jonathan Richard Shewchuk,Liquid Simulation on Lattice-Based Tetrahedral Meshes, 2007 Symposium on Computer Animation (San Diego, California), pages 219–228, August 2007. PDF (color, 4,782k, 10 pages). Here, we use isosurface stuffing (above) as part of an algorithm for simulating liquids with free surfaces. The graded meshes allow us to maintain fine detail on the liquid surface without excessive computational cost in the interior. The rendered surface is represented as a separate surface triangulation, at an even finer detail than the surface of the tetrahedral mesh. We exploit the regularity of the meshes for fast point location, needed for semi-Lagrangian advection of the velocities and the surface itself. We also introduce a thickening strategy to prevent the liquid from breaking up into sheets or droplets so thin that they disappear, falling below the finest resolution of the mesh. Bryan Matthew Klingner and Jonathan Richard Shewchuk,Aggressive Tetrahedral Mesh Improvement, Proceedings of the 16th International Meshing Roundtable (Seattle, Washington), pages 3–23, October 2007. PDF (color, 26,567k, 18 pages).Mesh clean-up software takes an existing mesh and improves the quality of its elements by way of operations such as smoothing (moving vertices to better locations) and topological transformations (replacing a small set of tetrahedra with better ones). Here, we demonstrate algorithms and software that so aggressively improve tetrahedral meshes that we obtain quality substantially better than that produced by any previous method for tetrahedral mesh generation or mesh improvement. Our main innovation is to augment the best traditional clean-up methods (including some from the Discrete Optimization Algorithms paper below) with topological transformations and combinatorial optimization algorithms that insert new vertices. Our publicly available software Stellar often improves a mesh so that all its dihedral angles are between 30o and 130o.
Bryan Matthew Klingner and Jonathan Richard Shewchuk,Aggressive Tetrahedral Mesh Improvement, Proceedings of the 16th International Meshing Roundtable (Seattle, Washington), pages 3–23, October 2007. PDF (color, 26,567k, 18 pages).Mesh clean-up software takes an existing mesh and improves the quality of its elements by way of operations such as smoothing (moving vertices to better locations) and topological transformations (replacing a small set of tetrahedra with better ones). Here, we demonstrate algorithms and software that so aggressively improve tetrahedral meshes that we obtain quality substantially better than that produced by any previous method for tetrahedral mesh generation or mesh improvement. Our main innovation is to augment the best traditional clean-up methods (including some from the Discrete Optimization Algorithms paper below) with topological transformations and combinatorial optimization algorithms that insert new vertices. Our publicly available software Stellar often improves a mesh so that all its dihedral angles are between 30o and 130o. Martin Wicke, Daniel Ritchie, Bryan M. Klingner, Sebastian Burke, Jonathan R. Shewchuk, and James F. O'Brien,Dynamic Local Remeshing for Elastoplastic Simulation, ACM Transactions on Graphics 29(4):49.1–49.11, July 2010. Special issue on Proceedings of SIGGRAPH 2010. PDF (color, 3,650k, 11 pages). We develop a dynamic finite element method for modeling elastoplastic materials undergoing extreme deformations and fracture, such as slime dripping from a ceiling or clay forced through an aperture. Radical changes in the shape of an object necessitate remeshing, but we must resample the strain field from the old mesh to the new one and thereby incur errors that manifest as artificial plasticity. We introduce two techniques to mitigate these errors. First, we have a new notion of “material space” that represents the configuration of the object with minimum internal strain, and we remesh in that space, rather than remesh in world space as some previous researchers have done. Second, we have algorithms for dynamic mesh generation that locally improve small regions of the mesh while leaving the majority undisturbed. Our dynamic remeshing techniques are a variant of our mesh improvement methods from the paper above.
Martin Wicke, Daniel Ritchie, Bryan M. Klingner, Sebastian Burke, Jonathan R. Shewchuk, and James F. O'Brien,Dynamic Local Remeshing for Elastoplastic Simulation, ACM Transactions on Graphics 29(4):49.1–49.11, July 2010. Special issue on Proceedings of SIGGRAPH 2010. PDF (color, 3,650k, 11 pages). We develop a dynamic finite element method for modeling elastoplastic materials undergoing extreme deformations and fracture, such as slime dripping from a ceiling or clay forced through an aperture. Radical changes in the shape of an object necessitate remeshing, but we must resample the strain field from the old mesh to the new one and thereby incur errors that manifest as artificial plasticity. We introduce two techniques to mitigate these errors. First, we have a new notion of “material space” that represents the configuration of the object with minimum internal strain, and we remesh in that space, rather than remesh in world space as some previous researchers have done. Second, we have algorithms for dynamic mesh generation that locally improve small regions of the mesh while leaving the majority undisturbed. Our dynamic remeshing techniques are a variant of our mesh improvement methods from the paper above. Pascal Clausen, Martin Wicke, Jonathan R. Shewchuk, and James F. O'Brien,Simulating Liquids and Solid-Liquid Interactions with Lagrangian Meshes, ACM Transactions on Graphics 32(2), April 2013. PDF (color, 15,031k, 15 pages). We develop a Lagrangian finite element method that simulates the behavior of liquids and solids in a unified framework. We continue the development of dynamic mesh generation algorithms from the two papers above; our dynamic mesh improvement library Stellar maintains a high-quality tetrahedral mesh even as it is advected by fluid flow. Topological changes in the domain are explicitly treated with local mesh splitting and merging. We conserve volume and momentum, locally and globally, by assigning each element an independent rest volume and adjusting it to correct for deviations during remeshing and collisions. Our method models surface tension with an implicit formulation based on surface energies computed on the boundary of the volume mesh. With this method we can model elastic, plastic, and liquid materials in a single mesh, with no need for explicit coupling. We also model heat diffusion and thermoelastic effects, which allow us to simulate phase changes like melting.
Pascal Clausen, Martin Wicke, Jonathan R. Shewchuk, and James F. O'Brien,Simulating Liquids and Solid-Liquid Interactions with Lagrangian Meshes, ACM Transactions on Graphics 32(2), April 2013. PDF (color, 15,031k, 15 pages). We develop a Lagrangian finite element method that simulates the behavior of liquids and solids in a unified framework. We continue the development of dynamic mesh generation algorithms from the two papers above; our dynamic mesh improvement library Stellar maintains a high-quality tetrahedral mesh even as it is advected by fluid flow. Topological changes in the domain are explicitly treated with local mesh splitting and merging. We conserve volume and momentum, locally and globally, by assigning each element an independent rest volume and adjusting it to correct for deviations during remeshing and collisions. Our method models surface tension with an implicit formulation based on surface energies computed on the boundary of the volume mesh. With this method we can model elastic, plastic, and liquid materials in a single mesh, with no need for explicit coupling. We also model heat diffusion and thermoelastic effects, which allow us to simulate phase changes like melting.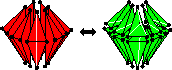 Two Discrete Optimization Algorithms for the Topological Improvement of Tetrahedral Meshes, unpublished manuscript, 2002. PostScript (295k, 11 pages), PDF (168k, 11 pages). This tutorial studies two local topological transformations for improving tetrahedral meshes: edge removal and_multi-face removal_. Given a selected edge, edge removal deletes all the tetrahedra that contain the edge, and replaces them with other tetrahedra. I work out in detail (and attempt to popularize) an algorithm of Klincsek for finding the optimal set of new tetrahedra. The multi-face removal operation is the inverse of the edge removal operation. I give a new algorithm for finding the optimal multi-face removal operation that involves a selected face of the tetrahedralization. These algorithms are part of our tetrahedral mesh improvement software described in the papers above.
Two Discrete Optimization Algorithms for the Topological Improvement of Tetrahedral Meshes, unpublished manuscript, 2002. PostScript (295k, 11 pages), PDF (168k, 11 pages). This tutorial studies two local topological transformations for improving tetrahedral meshes: edge removal and_multi-face removal_. Given a selected edge, edge removal deletes all the tetrahedra that contain the edge, and replaces them with other tetrahedra. I work out in detail (and attempt to popularize) an algorithm of Klincsek for finding the optimal set of new tetrahedra. The multi-face removal operation is the inverse of the edge removal operation. I give a new algorithm for finding the optimal multi-face removal operation that involves a selected face of the tetrahedralization. These algorithms are part of our tetrahedral mesh improvement software described in the papers above. Florian Hecht, Yeon Jin Lee, Jonathan R. Shewchuk, and James F. O'Brien,Updated Sparse Cholesky Factors for Corotational Elastodynamics, ACM Transactions on Graphics 31(5):123.1–123.13, October 2012. PDF (color, 24,436k, 13 pages). We introduce warp-canceling corotation, a nonlinear finite element formulation for elastodynamic simulation that achieves fast performance by making only partial or delayed changes to the simulation's linearized system matrices. This formulation combines the widely used corotational finite element method with stiffness warping so that changes in the per-element rotations are initially approximated by inexpensive per-node rotations. When the errors of this approximation grow too large, the per-element rotations are selectively corrected by updating parts of the matrix chosen according to locally measured errors. These changes to the system matrix are propagated to its sparse Cholesky factor by incremental updates that are much faster than refactoring the matrix from scratch. A nested dissection ordering of the system matrix gives rise to a hierarchical factorization in which changes to the system matrix cause limited, well-structured changes to the Cholesky factor. Because our method requires computing only partial updates of the Cholesky factor, it is substantially faster than full refactorization and outperforms widely used iterative methods such as preconditioned conjugate gradients, but it realizes the stability and scalability of a sparse direct method. Unlike iterative methods, our method's performance does not slow for stiffer materials; rather, it improves.
Florian Hecht, Yeon Jin Lee, Jonathan R. Shewchuk, and James F. O'Brien,Updated Sparse Cholesky Factors for Corotational Elastodynamics, ACM Transactions on Graphics 31(5):123.1–123.13, October 2012. PDF (color, 24,436k, 13 pages). We introduce warp-canceling corotation, a nonlinear finite element formulation for elastodynamic simulation that achieves fast performance by making only partial or delayed changes to the simulation's linearized system matrices. This formulation combines the widely used corotational finite element method with stiffness warping so that changes in the per-element rotations are initially approximated by inexpensive per-node rotations. When the errors of this approximation grow too large, the per-element rotations are selectively corrected by updating parts of the matrix chosen according to locally measured errors. These changes to the system matrix are propagated to its sparse Cholesky factor by incremental updates that are much faster than refactoring the matrix from scratch. A nested dissection ordering of the system matrix gives rise to a hierarchical factorization in which changes to the system matrix cause limited, well-structured changes to the Cholesky factor. Because our method requires computing only partial updates of the Cholesky factor, it is substantially faster than full refactorization and outperforms widely used iterative methods such as preconditioned conjugate gradients, but it realizes the stability and scalability of a sparse direct method. Unlike iterative methods, our method's performance does not slow for stiffer materials; rather, it improves.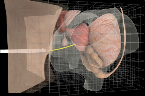 Nuttapong Chentanez, Ron Alterovitz, Daniel Ritchie, Lita Cho, Kris K. Hauser, Ken Goldberg, Jonathan R. Shewchuk, and James F. O'Brien,Interactive Simulation of Surgical Needle Insertion and Steering, ACM Transactions on Graphics 28(3):88.1–88.10, August 2009. Special issue on Proceedings of SIGGRAPH 2009. PDF (color, 6,580k, 10 pages). Clinical procedures such as biopsies, injections, and neurosurgery involve inserting a needle into tissue; here we focus on brachytherapy cancer treatment with a steerable needle, in which radioactive seeds are injected into a prostate gland to locally irradiate tumors. Needle insertion deforms body tissues, making it difficult to accurately place the needle tip while avoiding vulnerable vessels and nerves. We describe an interactive, real-time simulator of needle insertion that might lead to software for training surgeons and planning surgeries based on medical images from patients. The simulator models the coupling between a steerable needle and deformable tissue as a linear complementarity problem. A key part of our simulator is a novel algorithm for dynamic local remeshing that quickly enforces the conformity of a tetrahedral tissue mesh to a curvilinear needle path, enabling accurate computation of contact forces. Because a one-dimensional needle intersects the tissue mesh in simple ways, we can use a simple and fast dynamic meshing algorithm that keeps the quality of the modified tetrahedra high in practice.
Nuttapong Chentanez, Ron Alterovitz, Daniel Ritchie, Lita Cho, Kris K. Hauser, Ken Goldberg, Jonathan R. Shewchuk, and James F. O'Brien,Interactive Simulation of Surgical Needle Insertion and Steering, ACM Transactions on Graphics 28(3):88.1–88.10, August 2009. Special issue on Proceedings of SIGGRAPH 2009. PDF (color, 6,580k, 10 pages). Clinical procedures such as biopsies, injections, and neurosurgery involve inserting a needle into tissue; here we focus on brachytherapy cancer treatment with a steerable needle, in which radioactive seeds are injected into a prostate gland to locally irradiate tumors. Needle insertion deforms body tissues, making it difficult to accurately place the needle tip while avoiding vulnerable vessels and nerves. We describe an interactive, real-time simulator of needle insertion that might lead to software for training surgeons and planning surgeries based on medical images from patients. The simulator models the coupling between a steerable needle and deformable tissue as a linear complementarity problem. A key part of our simulator is a novel algorithm for dynamic local remeshing that quickly enforces the conformity of a tetrahedral tissue mesh to a curvilinear needle path, enabling accurate computation of contact forces. Because a one-dimensional needle intersects the tissue mesh in simple ways, we can use a simple and fast dynamic meshing algorithm that keeps the quality of the modified tetrahedra high in practice.
Streaming Geometric Computation
A STREAMING COMPUTATION MAKES A SMALL NUMBER of sequential passes over a data file (ideally, one pass), and processes the data using a memory buffer whose size is a fraction of the stream length. Streaming allows us to compute Delaunay triangulations of billions of points on an ordinary laptop computer—and amazingly, to attain faster speeds than ordinary in-core triangulators. We also have streaming implementations of several standard GIS computations, such as converting Triangulated Irregular Networks (TINs, which are unstructured triangulations used to interpolate elevation fields) into Digital Elevation Maps (DEMs), and computing isolines. A major benefit of streaming is quick feedback. For example, a user can pipe the triangulator's output to our streaming isocontour extraction module, whose output is piped to a visualization module. Isocontours begin to appear within minutes or seconds, because streaming modules produce output while still consuming input. If they look wrong, the user can abort the pipeline and restart all the streaming components with different parameters. With other methods, users must wait hours for the computations to finish before glimpsing the results.
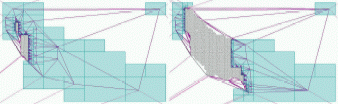 Martin Isenburg, Yuanxin Liu, Jonathan Shewchuk, and Jack Snoeyink,Streaming Computation of Delaunay Triangulations, ACM Transactions on Graphics 25(3):1049–1056, July 2006. Special issue on Proceedings of SIGGRAPH 2006. PDF (color, 9,175k, 8 pages). We compute a billion-triangle terrain representation for the Neuse River system from 11.2 GB of LIDAR data in 48 minutes using only 70 MB of memory on a laptop with two hard drives. This is a factor of twelve faster than the previous fastest out-of-core Delaunay triangulation software. We also construct a nine-billion-triangle, 152 GB triangulation in under seven hours using 166 MB of main memory. The main new idea in our streaming Delaunay triangulators is_spatial finalization_. We partition space into regions, and include _finalization tags_in the stream that indicate when no more points in the stream will fall in specified regions. Our triangulators certify triangles or tetrahedra as Delaunay when the finalization tags show it is safe to do so. This make it possible to write them out early, freeing up memory to read more from the input stream. Because only the unfinalized parts of a triangulation are resident in memory, the memory footprint remains small.
Martin Isenburg, Yuanxin Liu, Jonathan Shewchuk, and Jack Snoeyink,Streaming Computation of Delaunay Triangulations, ACM Transactions on Graphics 25(3):1049–1056, July 2006. Special issue on Proceedings of SIGGRAPH 2006. PDF (color, 9,175k, 8 pages). We compute a billion-triangle terrain representation for the Neuse River system from 11.2 GB of LIDAR data in 48 minutes using only 70 MB of memory on a laptop with two hard drives. This is a factor of twelve faster than the previous fastest out-of-core Delaunay triangulation software. We also construct a nine-billion-triangle, 152 GB triangulation in under seven hours using 166 MB of main memory. The main new idea in our streaming Delaunay triangulators is_spatial finalization_. We partition space into regions, and include _finalization tags_in the stream that indicate when no more points in the stream will fall in specified regions. Our triangulators certify triangles or tetrahedra as Delaunay when the finalization tags show it is safe to do so. This make it possible to write them out early, freeing up memory to read more from the input stream. Because only the unfinalized parts of a triangulation are resident in memory, the memory footprint remains small. Videoplus leaflet:Martin Isenburg, Yuanxin Liu, Jonathan Shewchuk, and Jack Snoeyink,Illustrating the Streaming Construction of 2D Delaunay Triangulations, Proceedings of the Fifteenth Video Review of Computational Geometry(video) andProceedings of the Twenty-Second Annual Symposium on Computational Geometry (Sedona, Arizona), pages 481–482, Association for Computing Machinery, June 2006(leaflet). PDF (color, 766k, 2 pages). Thevideo(your choice of QT/mpeg4 or DivX) demonstrates the implementation described in our SIGGRAPH paper (above), and the leaflet describes the video.
Videoplus leaflet:Martin Isenburg, Yuanxin Liu, Jonathan Shewchuk, and Jack Snoeyink,Illustrating the Streaming Construction of 2D Delaunay Triangulations, Proceedings of the Fifteenth Video Review of Computational Geometry(video) andProceedings of the Twenty-Second Annual Symposium on Computational Geometry (Sedona, Arizona), pages 481–482, Association for Computing Machinery, June 2006(leaflet). PDF (color, 766k, 2 pages). Thevideo(your choice of QT/mpeg4 or DivX) demonstrates the implementation described in our SIGGRAPH paper (above), and the leaflet describes the video.- Talk slides: Streaming Construction of Delaunay Triangulations. PDF (color, 2,058k, 96 pages).
 Martin Isenburg, Yuanxin Liu, Jonathan Shewchuk, Jack Snoeyink, and Tim Thirion,Generating Raster DEM from Mass Points via TIN Streaming, Proceedings of the Fourth International Conference on Geographic Information Science (GIScience 2006, Münster, Germany), September 2006. PostScript (color, 16,554k, 13 pages). PDF (color, 490k, 13 pages).
Martin Isenburg, Yuanxin Liu, Jonathan Shewchuk, Jack Snoeyink, and Tim Thirion,Generating Raster DEM from Mass Points via TIN Streaming, Proceedings of the Fourth International Conference on Geographic Information Science (GIScience 2006, Münster, Germany), September 2006. PostScript (color, 16,554k, 13 pages). PDF (color, 490k, 13 pages). Martin Isenburg, Peter Lindstrom, Stefan Gumhold, and Jonathan Shewchuk,Streaming Compression of Tetrahedral Volume Meshes, Proceedings: Graphics Interface 2006 (Quebec City, Quebec, Canada), pages 115–121, June 2006. PDF (color, 3,821k, 7 pages).
Martin Isenburg, Peter Lindstrom, Stefan Gumhold, and Jonathan Shewchuk,Streaming Compression of Tetrahedral Volume Meshes, Proceedings: Graphics Interface 2006 (Quebec City, Quebec, Canada), pages 115–121, June 2006. PDF (color, 3,821k, 7 pages).
Finite Element Quality
IT IS NOT EASY TO FORMULATE the problem that a mesh generator is to solve. The natural first question is how to characterize good and bad triangles and tetrahedra based on their sizes and shapes. The answer to that question depends on the application. The universal concern is that the errors introduced by interpolation be as small as possible. In the finite element method, another concern (with different implications) is that the condition numbers of the stiffness matrices be small. Forty-odd years after the invention of the finite element method, our understanding of the relationship between mesh geometry, numerical accuracy, and stiffness matrix conditioning remains incomplete, especially in anisotropic cases. The following papers examine these issues for linear elements, and present error bounds and quality measures to help guide numerical analysts, researchers in triangulation and mesh generation, and application writers in graphics and geographic information systems.
 What Is a Good Linear Finite Element? Interpolation, Conditioning, Anisotropy, and Quality Measures, unpublished preprint, 2002. COMMENTS NEEDED! Help me improve this manuscript. If you read this, please send feedback. PostScript (5,336k, 66 pages), PDF (1,190k, 66 pages). Why are elements with tiny angles harmless for interpolation, but deadly for stiffness matrix conditioning? Why are long, thin elements with angles near 180o terrible in isotropic cases but perfectly acceptable, if they're aligned properly, for anisotropic PDEs whose solutions have anisotropic curvature? Why do elements that are too long and thin sometimes offer unexpectedly accurate PDE solutions? Why can interpolation error, discretization error, and stiffness matrix conditioning sometimes have a three-way disagreement about the aspect ratio and alignment of the ideal element? Why do scale-invariant element quality measures often lead to incorrect conclusions about how to improve a finite element mesh? Why is the popular inradius-to-circumradius ratio such an ineffective quality measure for optimization-based mesh smoothing? All is revealed here.
What Is a Good Linear Finite Element? Interpolation, Conditioning, Anisotropy, and Quality Measures, unpublished preprint, 2002. COMMENTS NEEDED! Help me improve this manuscript. If you read this, please send feedback. PostScript (5,336k, 66 pages), PDF (1,190k, 66 pages). Why are elements with tiny angles harmless for interpolation, but deadly for stiffness matrix conditioning? Why are long, thin elements with angles near 180o terrible in isotropic cases but perfectly acceptable, if they're aligned properly, for anisotropic PDEs whose solutions have anisotropic curvature? Why do elements that are too long and thin sometimes offer unexpectedly accurate PDE solutions? Why can interpolation error, discretization error, and stiffness matrix conditioning sometimes have a three-way disagreement about the aspect ratio and alignment of the ideal element? Why do scale-invariant element quality measures often lead to incorrect conclusions about how to improve a finite element mesh? Why is the popular inradius-to-circumradius ratio such an ineffective quality measure for optimization-based mesh smoothing? All is revealed here. What Is a Good Linear Element? Interpolation, Conditioning, and Quality Measures, Eleventh International Meshing Roundtable (Ithaca, New York), pages 115–126, Sandia National Laboratories, September 2002. PostScript (1,083k, 12 pages), PDF (250k, 12 pages). A greatly abbreviated version (omitting the anisotropic cases, the derivations, and the discussions of discretization error and time-dependent problems) of the manuscript above.
What Is a Good Linear Element? Interpolation, Conditioning, and Quality Measures, Eleventh International Meshing Roundtable (Ithaca, New York), pages 115–126, Sandia National Laboratories, September 2002. PostScript (1,083k, 12 pages), PDF (250k, 12 pages). A greatly abbreviated version (omitting the anisotropic cases, the derivations, and the discussions of discretization error and time-dependent problems) of the manuscript above.- Talk slides: What Is a Good Linear Finite Element? Interpolation, Conditioning, Anisotropy, and Quality Measures. PDF (color, 316k, 32 pages).An overview of the basic bounds on interpolation errors and maximum eigenvalues of element stiffness matrices, as well as the quality measures associated with them. Includes a brief discussion of how anisotropy affects these bounds and the shape of the ideal element.
Constrained Delaunay Triangulations
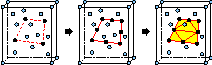
THE CONSTRAINED DELAUNAY TRIANGULATION (CDT) is a fundamental two-dimensional geometric structure with applications in interpolation, rendering, geography, and mesh generation. The most commonly implemented algorithm for constructing a CDT begins with an ordinary Delaunay triangulation and inserts constraining edges, often called segments, one by one. One of our papers shows that segments can be inserted in linear time, and investigates the expected running time of inserting segments in random order.
Prior to my work below, the CDT had not been generalized to higher dimensions, and it can never be fully generalized because not every polyhedron has a constrained tetrahedralization (allowing no additional vertices). Here, however, I prove that there is an easily tested condition that guarantees that a polyhedron (or piecewise linear domain) in three or more dimensions does have a constrained Delaunay triangulation. (A domain that satisfies the condition is said to be_edge-protected_ in three dimenions, or_ridge-protected_ in general dimensions.)
Suppose you want to tetrahedralize a three-dimensional domain. The result implies that if you insert enough extra vertices on the boundary of a polygon to recover its edges in a Delaunay tetrahedralization (in other words, if you make it be edge-protected) then you can recover the polygon's interior for free—that is, you can force the triangular faces of the tetrahedralization to conform to the polygon without inserting yet more vertices. This method of polygon recovery is immediately useful for mesh generation or the interpolation of discontinuous functions. (The result also fills a theoretical hole in my dissertation by showing that it is safe to delete a vertex from a constrained Delaunay tetrahedralization in the circumstances where my “diametral lens” algorithm does so.)
I provide two algorithms for constructing general-dimensional constrained Delaunay triangulations that are fast enough to be useful in practice. One is based on bistellar flips (which swap a few tetrahedra for a few others), and one is a sweep algorithm. The flip algorithm is easier to implement, and is probably usually faster in practice. However, the sweep algorithm works on almost every input that has a CDT, whereas the flip algorithm works only on ridge-protected inputs. The question of which algorithm is asymptotically faster is tricky—the answer depends on the size of the output, and is different for a worst-case input than for a random input; see the flip algorithm paper for details. See the “Strange Complexity” paper to find out why the sweep algorithm doesn't work on every input that has a CDT.
- Jonathan Richard Shewchuk and Brielin C. Brown,Fast Segment Insertion and Incremental Construction of Constrained Delaunay Triangulations, Computational Geometry: Theory and Applications 48(8):554–574, September 2015. PostScript (536k, 29 pages), PDF (310k, 29 pages). Conference version:Proceedings of the Twenty-Ninth Annual Symposium on Computational Geometry (Rio de Janeiro, Brazil), pages 299–308, Association for Computing Machinery, June 2013. PostScript (320k, 10 pages), PDF (213k, 10 pages). The most common way to construct a constrained Delaunay triangulation (CDT) in the plane is to first construct the Delaunay triangulation of the input vertices, then incrementally insert the input segments one by one. We give a randomized algorithm for inserting a segment into a CDT in expected time linear in the number of edges the segment crosses. We implemented it, and we show that it is faster than gift-wrapping for segments that cross many edges. We also show that a simple algorithm for segment location, which precedes segment insertion, is fast enough never to be a bottleneck in CDT construction. A result of Agarwal, Arge, and Yi implies that randomized incremental construction of CDTs by our segment insertion algorithm takes expected O(n log n + n log2 k) time. We show that this bound is tight by deriving a matching lower bound. Although there are CDT construction algorithms guaranteed to run in O(n log n) time, incremental CDT construction is easier to program and competitive in practice. Note that the symposium paper studies only two-dimensional CDTs, whereas the journal article partly extends the analysis (albeit not the linear-time insertion algorithm) to three dimensions.
- Talk slides: Constrained Delaunay Tetrahedralizations, Bistellar Flips, and Provably Good Boundary Recovery. PDF (color, 233k, 49 pages).Slides from a talk that covers the CDT existence theorem, the vertex insertion algorithm for provably good boundary recovery, and the flip algorithm for inserting a polygon into a CDT. You can evenwatch me give this talk at the Mathematical Sciences Research Institute.
 Constrained Delaunay Tetrahedralizations and Provably Good Boundary Recovery, Eleventh International Meshing Roundtable (Ithaca, New York), pages 193–204, Sandia National Laboratories, September 2002. PostScript (410k, 12 pages), PDF (187k, 12 pages). A basic guide: why constrained Delaunay tetrahedralizations are good for boundary recovery, and how to use them effectively. Includes an algorithm for inserting vertices to recover the segments of an input domain (e.g. a polyhedron), and high-level descriptions of two algorithms for constructing the constrained Delaunay tetrahedralization of the augmented domain. (Unfortunately, this paper predates the flip algorithm, which I think is usually a better choice in practice.) “Provably good boundary recovery” means that no edge of the final tetrahedralization is shorter than one quarter of the local feature size, so any subsequent Delaunay refinement will not be forced to create unnecessarily small elements. (An exception is any edge that spans two segments of the input domain separated by a small angle; a weaker bound applies to such an edge.) Aimed at programmers and practitioners. This paper discusses the three-dimensional case only, unlike most of the papers below.
Constrained Delaunay Tetrahedralizations and Provably Good Boundary Recovery, Eleventh International Meshing Roundtable (Ithaca, New York), pages 193–204, Sandia National Laboratories, September 2002. PostScript (410k, 12 pages), PDF (187k, 12 pages). A basic guide: why constrained Delaunay tetrahedralizations are good for boundary recovery, and how to use them effectively. Includes an algorithm for inserting vertices to recover the segments of an input domain (e.g. a polyhedron), and high-level descriptions of two algorithms for constructing the constrained Delaunay tetrahedralization of the augmented domain. (Unfortunately, this paper predates the flip algorithm, which I think is usually a better choice in practice.) “Provably good boundary recovery” means that no edge of the final tetrahedralization is shorter than one quarter of the local feature size, so any subsequent Delaunay refinement will not be forced to create unnecessarily small elements. (An exception is any edge that spans two segments of the input domain separated by a small angle; a weaker bound applies to such an edge.) Aimed at programmers and practitioners. This paper discusses the three-dimensional case only, unlike most of the papers below.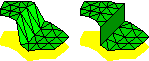 General-Dimensional Constrained Delaunay and Constrained Regular Triangulations, I: Combinatorial Properties. Discrete & Computational Geometry 39(1–3):580–637, March 2008. PostScript (865k, 54 pages), PDF (447k, 54 pages). This manuscript lays down the combinatorial foundations of CDTs and weighted CDTs. It begins by proving that many properties of Delaunay triangulations (of any dimension) generalize to constrained Delaunay triangulations—in particular, the Delaunay Lemma, which states that a triangulation is a weighted CDT if and only if every (_d_–1)-dimensional face is either “locally regular” (locally convex on the lifting map) or a constraining face. Next, the manuscript shows that (weighted) CDTs have several optimality properties when used for piecewise linear interpolation. It culminates with the proof that if an input is weakly ridge-protected (a less restrictive condition than ridge-protected), it has a CDT. This proof also applies to weighted CDTs. This paper is the ideal starting point for researchers who want to work with CDTs of dimension higher than two, and it is the foundation of the correctness proofs of my CDT construction algorithms. For those who don't want to read the proofs, the introduction summarizes the results and how to use them. Aimed at computational geometers. Discusses the general-dimensional case.
General-Dimensional Constrained Delaunay and Constrained Regular Triangulations, I: Combinatorial Properties. Discrete & Computational Geometry 39(1–3):580–637, March 2008. PostScript (865k, 54 pages), PDF (447k, 54 pages). This manuscript lays down the combinatorial foundations of CDTs and weighted CDTs. It begins by proving that many properties of Delaunay triangulations (of any dimension) generalize to constrained Delaunay triangulations—in particular, the Delaunay Lemma, which states that a triangulation is a weighted CDT if and only if every (_d_–1)-dimensional face is either “locally regular” (locally convex on the lifting map) or a constraining face. Next, the manuscript shows that (weighted) CDTs have several optimality properties when used for piecewise linear interpolation. It culminates with the proof that if an input is weakly ridge-protected (a less restrictive condition than ridge-protected), it has a CDT. This proof also applies to weighted CDTs. This paper is the ideal starting point for researchers who want to work with CDTs of dimension higher than two, and it is the foundation of the correctness proofs of my CDT construction algorithms. For those who don't want to read the proofs, the introduction summarizes the results and how to use them. Aimed at computational geometers. Discusses the general-dimensional case. A Condition Guaranteeing the Existence of Higher-Dimensional Constrained Delaunay Triangulations, Proceedings of the Fourteenth Annual Symposium on Computational Geometry (Minneapolis, Minnesota), pages 76–85, Association for Computing Machinery, June 1998. PostScript (328k, 10 pages), PDF (181k, 10 pages). An early version of the CDT existence proof, which is the most difficult proof I've ever done. This version of the proof is shorter than the more general and rigorous proof in the paper above, but it also has some unnecessary complications that I excised from the later version. The proof is tough reading, but you don't need to understand it to use the result. Also includes a discussion of a slow-but-simple gift-wrapping algorithm for constructing a constrained Delaunay triangulation. This paper does not discuss weighted CDTs (constrained regular triangulations); see the paper above for that. Aimed at computational geometers. Discusses the general-dimensional case.
A Condition Guaranteeing the Existence of Higher-Dimensional Constrained Delaunay Triangulations, Proceedings of the Fourteenth Annual Symposium on Computational Geometry (Minneapolis, Minnesota), pages 76–85, Association for Computing Machinery, June 1998. PostScript (328k, 10 pages), PDF (181k, 10 pages). An early version of the CDT existence proof, which is the most difficult proof I've ever done. This version of the proof is shorter than the more general and rigorous proof in the paper above, but it also has some unnecessary complications that I excised from the later version. The proof is tough reading, but you don't need to understand it to use the result. Also includes a discussion of a slow-but-simple gift-wrapping algorithm for constructing a constrained Delaunay triangulation. This paper does not discuss weighted CDTs (constrained regular triangulations); see the paper above for that. Aimed at computational geometers. Discusses the general-dimensional case.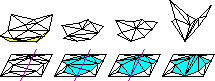 Updating and Constructing Constrained Delaunay and Constrained Regular Triangulations by Flips, Proceedings of the Nineteenth Annual Symposium on Computational Geometry (San Diego, California), pages 181–190, Association for Computing Machinery, June 2003. PostScript (545k, 14 pages including a four-page appendix not in the published version), PDF (244k, 14 pages). If you want to incrementally update a constrained Delaunay triangulation, you need four operations: inserting and deleting a polygon, and inserting and deleting a vertex. (To “insert a polygon” is to force the faces of the CDT to respect the polygon; to “delete a polygon” is to relax the polygon constraint so the CDT can act a little more Delaunay and a little less constrained.) This paper gives algorithms for the first two, based on simple bistellar flips. A sweep algorithm for deleting a vertex appears in the paper below (and it is trivially converted to a flip algorithm). Finally, Barry Joe's flip algorithm for inserting a vertex into a Delaunay triangulation is easily modified to work in a CDT. These operations work in any dimensionality, and they can all be applied to the more general class of_constrained regular triangulations_ (which include CDTs).
Updating and Constructing Constrained Delaunay and Constrained Regular Triangulations by Flips, Proceedings of the Nineteenth Annual Symposium on Computational Geometry (San Diego, California), pages 181–190, Association for Computing Machinery, June 2003. PostScript (545k, 14 pages including a four-page appendix not in the published version), PDF (244k, 14 pages). If you want to incrementally update a constrained Delaunay triangulation, you need four operations: inserting and deleting a polygon, and inserting and deleting a vertex. (To “insert a polygon” is to force the faces of the CDT to respect the polygon; to “delete a polygon” is to relax the polygon constraint so the CDT can act a little more Delaunay and a little less constrained.) This paper gives algorithms for the first two, based on simple bistellar flips. A sweep algorithm for deleting a vertex appears in the paper below (and it is trivially converted to a flip algorithm). Finally, Barry Joe's flip algorithm for inserting a vertex into a Delaunay triangulation is easily modified to work in a CDT. These operations work in any dimensionality, and they can all be applied to the more general class of_constrained regular triangulations_ (which include CDTs).
By starting with a Delaunay (or regular) triangulation and incrementally inserting polygons one by one, you can construct the constrained Delaunay (or constrained regular) triangulation of a ridge-protected input in O(nv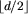 + 1 log nv) time, where nv is the number of input vertices and d is the dimensionality. In odd dimensions (including three dimensions, which is what I care about most) this is within a factor of log nv of worst-case optimal. The algorithm is likely to take only O(nv log nv) time in many practical cases. Aimed at both programmers and computational geometers. Discusses the general-dimensional case, but most useful in three dimensions.
+ 1 log nv) time, where nv is the number of input vertices and d is the dimensionality. In odd dimensions (including three dimensions, which is what I care about most) this is within a factor of log nv of worst-case optimal. The algorithm is likely to take only O(nv log nv) time in many practical cases. Aimed at both programmers and computational geometers. Discusses the general-dimensional case, but most useful in three dimensions.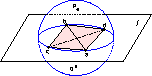 Hang Si and Jonathan Richard Shewchuk,Incrementally Constructing and Updating Constrained Delaunay Tetrahedralizations with Finite Precision Coordinates, Proceedings of the 21st International Meshing Roundtable (San Jose, California), pages 173–190, October 2012. PDF (881k, 18 pages). An experimental comparison of two recent algorithms for inserting a polygon into a CDT: my bistellar flip algorithm (see the paper above) and a cavity retriangulation algorithm of Si and Gärtner (Proceeding of the Fourteenth International Meshing Roundtable, September 2005). With respect to speed, there is no clear winner. We modify these algorithms to succeed in practice for polygons whose vertices deviate from exact coplanarity, which cause problems both theoretical and numerical. It proves to be easier to make Si and Gärtner's algorithm reliable than mine.
Hang Si and Jonathan Richard Shewchuk,Incrementally Constructing and Updating Constrained Delaunay Tetrahedralizations with Finite Precision Coordinates, Proceedings of the 21st International Meshing Roundtable (San Jose, California), pages 173–190, October 2012. PDF (881k, 18 pages). An experimental comparison of two recent algorithms for inserting a polygon into a CDT: my bistellar flip algorithm (see the paper above) and a cavity retriangulation algorithm of Si and Gärtner (Proceeding of the Fourteenth International Meshing Roundtable, September 2005). With respect to speed, there is no clear winner. We modify these algorithms to succeed in practice for polygons whose vertices deviate from exact coplanarity, which cause problems both theoretical and numerical. It proves to be easier to make Si and Gärtner's algorithm reliable than mine. Sweep Algorithms for Constructing Higher-Dimensional Constrained Delaunay Triangulations, Proceedings of the Sixteenth Annual Symposium on Computational Geometry (Hong Kong), pages 350–359, Association for Computing Machinery, June 2000. PostScript (352k, 10 pages), PDF (195k, 10 pages). Gives an O(nvns)-time sweep algorithm for constructing a constrained Delaunay triangulation, where nv is the number of input vertices, and ns is the number of simplices in the triangulation. (The algorithm is likely to be faster in most practical cases.) The running time improves to O(ns log nv) for star-shaped polytopes, yielding an efficient way to delete a vertex from a CDT.
Sweep Algorithms for Constructing Higher-Dimensional Constrained Delaunay Triangulations, Proceedings of the Sixteenth Annual Symposium on Computational Geometry (Hong Kong), pages 350–359, Association for Computing Machinery, June 2000. PostScript (352k, 10 pages), PDF (195k, 10 pages). Gives an O(nvns)-time sweep algorithm for constructing a constrained Delaunay triangulation, where nv is the number of input vertices, and ns is the number of simplices in the triangulation. (The algorithm is likely to be faster in most practical cases.) The running time improves to O(ns log nv) for star-shaped polytopes, yielding an efficient way to delete a vertex from a CDT. Nicolas Grislain and Jonathan Richard Shewchuk,The Strange Complexity of Constrained Delaunay Triangulation, Proceedings of the Fifteenth Canadian Conference on Computational Geometry (Halifax, Nova Scotia), pages 89–93, August 2003. PostScript (195k, 4 pages), PDF (73k, 4 pages). The problem of constructing a constrained Delaunay tetrahedralization has the unusual status (for a small-dimensional problem) of being NP-hard only for degenerate inputs, namely those with subsets of five or more cospherical vertices. This paper proves one half of that statement: it is NP-hard to decide whether a polyhedron has a constrained Delaunay tetrahedralization. The paper on sweep algorithms (above) contains the proof of the other half: for a polyhedron (or more generally, a piecewise linear complex) with no five vertices lying on a common sphere, a polynomial-time algorithm constructs the CDT (if it exists) and thereby solves the decision problem. Freaky, eh?
Nicolas Grislain and Jonathan Richard Shewchuk,The Strange Complexity of Constrained Delaunay Triangulation, Proceedings of the Fifteenth Canadian Conference on Computational Geometry (Halifax, Nova Scotia), pages 89–93, August 2003. PostScript (195k, 4 pages), PDF (73k, 4 pages). The problem of constructing a constrained Delaunay tetrahedralization has the unusual status (for a small-dimensional problem) of being NP-hard only for degenerate inputs, namely those with subsets of five or more cospherical vertices. This paper proves one half of that statement: it is NP-hard to decide whether a polyhedron has a constrained Delaunay tetrahedralization. The paper on sweep algorithms (above) contains the proof of the other half: for a polyhedron (or more generally, a piecewise linear complex) with no five vertices lying on a common sphere, a polynomial-time algorithm constructs the CDT (if it exists) and thereby solves the decision problem. Freaky, eh?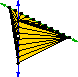 Stabbing Delaunay Tetrahedralizations, Discrete & Computational Geometry 32(3):339–343, October 2004. PostScript (143k, 4 pages), PDF (70k, 4 pages), HTML. This note answers (pessimistically) the formerly open question of how many tetrahedra in an _n_-point Delaunay tetrahedralization can be stabbed by a straight line. The answer: for a worst-case tetrahedralization, a line can intersect the interiors of
Stabbing Delaunay Tetrahedralizations, Discrete & Computational Geometry 32(3):339–343, October 2004. PostScript (143k, 4 pages), PDF (70k, 4 pages), HTML. This note answers (pessimistically) the formerly open question of how many tetrahedra in an _n_-point Delaunay tetrahedralization can be stabbed by a straight line. The answer: for a worst-case tetrahedralization, a line can intersect the interiors of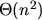 tetrahedra. In d dimensions, a line can stab the interiors of
tetrahedra. In d dimensions, a line can stab the interiors of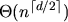 Delaunay _d_-simplices. The result explains why my sweep algorithm for constructing CDTs has a worst-case running time of O(nvns) and not O(_nv_2 +ns log nv). The difficulty of finding the worst-case example explains why the sweep algorithm is unlikely to take longer than O(_nv_2 +ns log nv) time on any real-world input.
Delaunay _d_-simplices. The result explains why my sweep algorithm for constructing CDTs has a worst-case running time of O(nvns) and not O(_nv_2 +ns log nv). The difficulty of finding the worst-case example explains why the sweep algorithm is unlikely to take longer than O(_nv_2 +ns log nv) time on any real-world input.
Surface Reconstruction
WE WISH TO RECONSTRUCT CLOSED SURFACESfrom simple geometric inputs like sets of points, sampled from the surface of a three-dimensional object using a laser range finder, or sets of polygons, which are often used as crude geometric models for rendering. However, the input data are rarely well-behaved. Laser range finders are imperfect physical devices that introduce random errors (noise) into the point coordinates, and often introduce points that don't lie anywhere near the surface (outliers) as well. Moreover, range finders can't usually scan an entire object's surface—portions of the surface are left undersampled or unsampled. Polygon inputs used for rendering are rarely topologically consistent—the polygons often have spurious intersections or leave small gaps in what should be a closed surface. For either type of input, we wish to generate a watertight surface that approximates the surface suggested by the data.
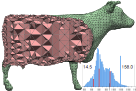
 Ravikrishna Kolluri, Jonathan Richard Shewchuk, and James F. O'Brien,Spectral Surface Reconstruction from Noisy Point Clouds, Symposium on Geometry Processing 2004 (Nice, France), pages 11–21, Eurographics Association, July 2004. PDF (color, 7,648k, 11 pages). Researchers have put forth several provably good Delaunay-based algorithms for surface reconstruction from unorganized point sets. However, in the presence of undersampling, noise, and outliers, they are neither “provably good” nor robust in practice. Our Eigencrust algorithm uses a spectral graph partitioner to make robust decisions about which Delaunay tetrahedra are inside the surface and which are outside. In practice, the Eigencrust algorithm handles undersampling, noise, and outliers quite well, while giving essentially the same results as the provably good Tight Cocone or Powercrust algorithms on “clean” point sets. (There is no theory in this paper, though.)
Ravikrishna Kolluri, Jonathan Richard Shewchuk, and James F. O'Brien,Spectral Surface Reconstruction from Noisy Point Clouds, Symposium on Geometry Processing 2004 (Nice, France), pages 11–21, Eurographics Association, July 2004. PDF (color, 7,648k, 11 pages). Researchers have put forth several provably good Delaunay-based algorithms for surface reconstruction from unorganized point sets. However, in the presence of undersampling, noise, and outliers, they are neither “provably good” nor robust in practice. Our Eigencrust algorithm uses a spectral graph partitioner to make robust decisions about which Delaunay tetrahedra are inside the surface and which are outside. In practice, the Eigencrust algorithm handles undersampling, noise, and outliers quite well, while giving essentially the same results as the provably good Tight Cocone or Powercrust algorithms on “clean” point sets. (There is no theory in this paper, though.)- Talk slides: Spectral Surface Reconstruction from Noisy Point Clouds. PDF (color, 1,758k, 53 pages). Slides from a talk on our paper above.
 Chen Shen, James F. O'Brien, and Jonathan R. Shewchuk,Interpolating and Approximating Implicit Surfaces from Polygon Soup, ACM Transactions on Graphics 23(3):896–904, August 2004. Special issue on Proceedings of SIGGRAPH 2004. PDF (color, 17,269k, 9 pages). The Moving Least Squares (MLS) method is a popular way to define an implicit surface that interpolates or approximates a set of points in three-dimensional space. But graphics programmers have made millions of polygonalized surface models; what if we want to interpolate whole polygons? Approximating a polygon as a bunch of points gives poor results. Instead, we show how to force an MLS function to have a specified value over each input polygon, by integrating constraints over triangles. Better yet, we show how to force the MLS function to have a specified gradient over each polygon as well, so that we can robustly specify which parts of space should be inside or outside the implicit surface—without creating undue oscillations in the MLS function. The trick is to define a different function on each input polygon, and use MLS to interpolate between _functions_—not just to interpolate between values (as the usual formulations of MLS for implicit surfaces do). This trick gives us profound control of an MLS function. Although our examples are all surfaces embedded in three-dimensional space, the techniques generalize to any dimensionality.
Chen Shen, James F. O'Brien, and Jonathan R. Shewchuk,Interpolating and Approximating Implicit Surfaces from Polygon Soup, ACM Transactions on Graphics 23(3):896–904, August 2004. Special issue on Proceedings of SIGGRAPH 2004. PDF (color, 17,269k, 9 pages). The Moving Least Squares (MLS) method is a popular way to define an implicit surface that interpolates or approximates a set of points in three-dimensional space. But graphics programmers have made millions of polygonalized surface models; what if we want to interpolate whole polygons? Approximating a polygon as a bunch of points gives poor results. Instead, we show how to force an MLS function to have a specified value over each input polygon, by integrating constraints over triangles. Better yet, we show how to force the MLS function to have a specified gradient over each polygon as well, so that we can robustly specify which parts of space should be inside or outside the implicit surface—without creating undue oscillations in the MLS function. The trick is to define a different function on each input polygon, and use MLS to interpolate between _functions_—not just to interpolate between values (as the usual formulations of MLS for implicit surfaces do). This trick gives us profound control of an MLS function. Although our examples are all surfaces embedded in three-dimensional space, the techniques generalize to any dimensionality.
Geometric Robustness
 GEOMETRIC PROGRAMS ARE SURPRISINGLY SUSCEPTIBLEto failure because of floating-point roundoff error. Robustness problems can be solved by using exact arithmetic, at the cost of reducing program speed by a factor of ten or more. Here, I describe a strategy for computing correct answers quickly when the inputs are floating-point values. (Much other research has dealt with the problem for integer inputs, which are less convenient for users but more tractable for robustness researchers.)
GEOMETRIC PROGRAMS ARE SURPRISINGLY SUSCEPTIBLEto failure because of floating-point roundoff error. Robustness problems can be solved by using exact arithmetic, at the cost of reducing program speed by a factor of ten or more. Here, I describe a strategy for computing correct answers quickly when the inputs are floating-point values. (Much other research has dealt with the problem for integer inputs, which are less convenient for users but more tractable for robustness researchers.)
To make robust geometric tests fast, I propose two new techniques (which can also be applied to other problems of numerical accuracy). First, I develop and prove the correctness of software-level algorithms for arbitrary precision floating-point arithmetic. These algorithms are refinements (especially with regard to speed) of algorithms suggested by Douglas Priest, and are roughly five times faster than the best available competing method when values of small or intermediate precision (hundreds or thousands of bits) are used. Second, I show how simple expressions (whose only operations are addition, subtraction, and multiplication) can be computed adaptively, trading off accuracy and speed as necessary to satisfy an error bound as quickly as possible. (This technique is probably applicable to any exact arithmetic scheme.) I apply these ideas to build fast, correct_orientation_ and incircle tests in two and three dimensions, and to make robust the implementations of two- and three-dimensional Delaunay triangulation in Triangle and Pyramid. Detailed measurements show that in most circumstances, these programs run nearly as quickly when using my adaptive predicates as they do using nonrobust predicates.
See my Robust Predicates page for more information about this research, or to obtain C source code for exact floating-point addition and multiplication and the robust geometric predicates.
 Adaptive Precision Floating-Point Arithmetic and Fast Robust Geometric Predicates, Discrete & Computational Geometry 18(3):305–363, October 1997. PostScript (775k, 55 pages), PDF (556k, 55 pages). Also appears as Chapter 6 of my dissertation.
Adaptive Precision Floating-Point Arithmetic and Fast Robust Geometric Predicates, Discrete & Computational Geometry 18(3):305–363, October 1997. PostScript (775k, 55 pages), PDF (556k, 55 pages). Also appears as Chapter 6 of my dissertation. Robust Adaptive Floating-Point Geometric Predicates, Proceedings of the Twelfth Annual Symposium on Computational Geometry (Philadelphia, Pennsylvania), pages 141–150, Association for Computing Machinery, May 1996. Abstract (with BibTeX citation), PostScript (310k, 10 pages), PDF (174k, 10 pages). A very abbreviated summary of the ideas from the full-length paper above.
Robust Adaptive Floating-Point Geometric Predicates, Proceedings of the Twelfth Annual Symposium on Computational Geometry (Philadelphia, Pennsylvania), pages 141–150, Association for Computing Machinery, May 1996. Abstract (with BibTeX citation), PostScript (310k, 10 pages), PDF (174k, 10 pages). A very abbreviated summary of the ideas from the full-length paper above.
The Quake Project
 PAPERS ABOUT THE QUAKE PROJECT, a multidisciplinary Grand Challenge Application Group studying ground motion in large basins during strong earthquakes, with the goal of characterizing the seismic response of the Los Angeles basin. The Quake Project is a joint effort between the departments of Computer Science and Civil and Environmental Engineering at Carnegie Mellon, the Southern California Earthquake Center, and the National University of Mexico. We've created some of the largest unstructured finite element simulations ever carried out; in particular, the papers below describe a simulation of ground motion during an aftershock of the 1994 Northridge Earthquake.
PAPERS ABOUT THE QUAKE PROJECT, a multidisciplinary Grand Challenge Application Group studying ground motion in large basins during strong earthquakes, with the goal of characterizing the seismic response of the Los Angeles basin. The Quake Project is a joint effort between the departments of Computer Science and Civil and Environmental Engineering at Carnegie Mellon, the Southern California Earthquake Center, and the National University of Mexico. We've created some of the largest unstructured finite element simulations ever carried out; in particular, the papers below describe a simulation of ground motion during an aftershock of the 1994 Northridge Earthquake.
 Hesheng Bao, Jacobo Bielak, Omar Ghattas, Loukas F. Kallivokas, David R. O'Hallaron, Jonathan R. Shewchuk, and Jifeng Xu,Large-scale Simulation of Elastic Wave Propagation in Heterogeneous Media on Parallel Computers, Computer Methods in Applied Mechanics and Engineering152(1–2):85–102, 22 January 1998. Abstract (with BibTex citation), Compressed PostScript (color, 4,262k, 34 pages)(Expands to 41,267k when uncompressed), PDF (color, 6,681k, 34 pages), HTML. The PostScript version uncompresses into six PostScript files. The first and last of these files are black-and-white. The middle four are huge and in full color.
Hesheng Bao, Jacobo Bielak, Omar Ghattas, Loukas F. Kallivokas, David R. O'Hallaron, Jonathan R. Shewchuk, and Jifeng Xu,Large-scale Simulation of Elastic Wave Propagation in Heterogeneous Media on Parallel Computers, Computer Methods in Applied Mechanics and Engineering152(1–2):85–102, 22 January 1998. Abstract (with BibTex citation), Compressed PostScript (color, 4,262k, 34 pages)(Expands to 41,267k when uncompressed), PDF (color, 6,681k, 34 pages), HTML. The PostScript version uncompresses into six PostScript files. The first and last of these files are black-and-white. The middle four are huge and in full color. Hesheng Bao, Jacobo Bielak, Omar Ghattas, David R. O'Hallaron, Loukas F. Kallivokas, Jonathan R. Shewchuk, and Jifeng Xu,Earthquake Ground Motion Modeling on Parallel Computers, Supercomputing '96 (Pittsburgh, Pennsylvania), November 1996. Abstract (with BibTeX citation), PostScript (color, 9,370k, 19 pages), PDF (color, 2,436k, 19 pages), HTML. An abbreviated version of the full-length paper above.
Hesheng Bao, Jacobo Bielak, Omar Ghattas, David R. O'Hallaron, Loukas F. Kallivokas, Jonathan R. Shewchuk, and Jifeng Xu,Earthquake Ground Motion Modeling on Parallel Computers, Supercomputing '96 (Pittsburgh, Pennsylvania), November 1996. Abstract (with BibTeX citation), PostScript (color, 9,370k, 19 pages), PDF (color, 2,436k, 19 pages), HTML. An abbreviated version of the full-length paper above.
 OUR SECRET TO PRODUCING such huge unstructured simulations? With the collaboration of David O'Hallaron, I've writtenArchimedes, a chain of tools for automating the construction of general-purpose finite element simulations on parallel computers. In addition to the mesh generators Triangle and Pyramid discussed above, Archimedes includes Slice, a mesh partitioner based on geometric recursive bisection;Parcel, which performs the surprisingly jumbled task of computing communication schedules and reordering partitioned mesh data into a format a parallel simulation can use; and Author, which generates parallel C code from high-level machine-independent programs (which are currently written by the civil engineers in our group). Archimedes has made it possible for the Quake Project to weather four consecutive changes in parallel architecture without missing a beat. The most recent information about Archimedes is contained in the Quake papers listed above. See also theArchimedes page.
OUR SECRET TO PRODUCING such huge unstructured simulations? With the collaboration of David O'Hallaron, I've writtenArchimedes, a chain of tools for automating the construction of general-purpose finite element simulations on parallel computers. In addition to the mesh generators Triangle and Pyramid discussed above, Archimedes includes Slice, a mesh partitioner based on geometric recursive bisection;Parcel, which performs the surprisingly jumbled task of computing communication schedules and reordering partitioned mesh data into a format a parallel simulation can use; and Author, which generates parallel C code from high-level machine-independent programs (which are currently written by the civil engineers in our group). Archimedes has made it possible for the Quake Project to weather four consecutive changes in parallel architecture without missing a beat. The most recent information about Archimedes is contained in the Quake papers listed above. See also theArchimedes page. 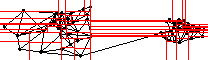 Anja Feldmann, Omar Ghattas, John R. Gilbert, Gary L. Miller, David R. O'Hallaron, Eric J. Schwabe, Jonathan R. Shewchuk, and Shang-Hua Teng,Automated Parallel Solution of Unstructured PDE Problems, unpublished manuscript, June 1996. PostScript (b/w, 1,708k, 19 pages), PostScript (color, 1,845k, 19 pages). Because color printing is expensive, you may want to print a complete black and white copy; then use a color printer to print the following file (which contains only the five color pages) and replace the corresponding black and white pages. PostScript (color pages only, 818k, 5 pages). A simple overview aimed at people who have little familiarity with finite element methods or parallel scientific computing.
Anja Feldmann, Omar Ghattas, John R. Gilbert, Gary L. Miller, David R. O'Hallaron, Eric J. Schwabe, Jonathan R. Shewchuk, and Shang-Hua Teng,Automated Parallel Solution of Unstructured PDE Problems, unpublished manuscript, June 1996. PostScript (b/w, 1,708k, 19 pages), PostScript (color, 1,845k, 19 pages). Because color printing is expensive, you may want to print a complete black and white copy; then use a color printer to print the following file (which contains only the five color pages) and replace the corresponding black and white pages. PostScript (color pages only, 818k, 5 pages). A simple overview aimed at people who have little familiarity with finite element methods or parallel scientific computing. Jonathan Richard Shewchuk and Omar Ghattas,A Compiler for Parallel Finite Element Methods with Domain-Decomposed Unstructured Meshes, Proceedings of the Seventh International Conference on Domain Decomposition Methods in Scientific and Engineering Computing (Pennsylvania State University), Contemporary Mathematics 180 (David E. Keyes and Jinchao Xu, editors), pages 445–450, American Mathematical Society, October 1993. Abstract, PostScript (color, 1,203k, 6 pages), PDF (color, 319k, 6 pages). A short discussion of our unusual way of storing distributed stiffness matrices and how it makes some domain decomposition algorithms easy to parallelize.
Jonathan Richard Shewchuk and Omar Ghattas,A Compiler for Parallel Finite Element Methods with Domain-Decomposed Unstructured Meshes, Proceedings of the Seventh International Conference on Domain Decomposition Methods in Scientific and Engineering Computing (Pennsylvania State University), Contemporary Mathematics 180 (David E. Keyes and Jinchao Xu, editors), pages 445–450, American Mathematical Society, October 1993. Abstract, PostScript (color, 1,203k, 6 pages), PDF (color, 319k, 6 pages). A short discussion of our unusual way of storing distributed stiffness matrices and how it makes some domain decomposition algorithms easy to parallelize. Eric J. Schwabe, Guy E. Blelloch, Anja Feldmann, Omar Ghattas, John R. Gilbert, Gary L. Miller, David R. O'Hallaron, Jonathan R. Shewchuk, and Shang-Hua Teng,A Separator-Based Framework for Automated Partitioning and Mapping of Parallel Algorithms for Numerical Solution of PDEs, Proceedings of the 1992 DAGS/PC Symposium, Dartmouth Institute for Advanced Graduate Studies, pages 48–62, June 1992. Abstract, PostScript (2,247k, 15 pages), PDF (464k, 15 pages). This paper is made obsolete by the manuscript “Automated Parallel Solution of Unstructured PDE Problems” above.
SEVERAL PAPERS ON THE COMPUTATION AND COMMUNICATION DEMANDSof the Quake Project's parallel finite element simulations, and what requirements such unstructured simulations will place on future parallel machines and networks. For designers of computer architecture who want to better understand unstructured applications.
Eric J. Schwabe, Guy E. Blelloch, Anja Feldmann, Omar Ghattas, John R. Gilbert, Gary L. Miller, David R. O'Hallaron, Jonathan R. Shewchuk, and Shang-Hua Teng,A Separator-Based Framework for Automated Partitioning and Mapping of Parallel Algorithms for Numerical Solution of PDEs, Proceedings of the 1992 DAGS/PC Symposium, Dartmouth Institute for Advanced Graduate Studies, pages 48–62, June 1992. Abstract, PostScript (2,247k, 15 pages), PDF (464k, 15 pages). This paper is made obsolete by the manuscript “Automated Parallel Solution of Unstructured PDE Problems” above.
SEVERAL PAPERS ON THE COMPUTATION AND COMMUNICATION DEMANDSof the Quake Project's parallel finite element simulations, and what requirements such unstructured simulations will place on future parallel machines and networks. For designers of computer architecture who want to better understand unstructured applications.  David O'Hallaron, Jonathan Richard Shewchuk, and Thomas Gross,Architectural Implications of a Family of Irregular Applications, Fourth International Symposium on High Performance Computer Architecture (Las Vegas, Nevada), February 1998. Abstract (with BibTex citation), PostScript (1,289k, 20 pages), PDF (218k, 20 pages).
David O'Hallaron, Jonathan Richard Shewchuk, and Thomas Gross,Architectural Implications of a Family of Irregular Applications, Fourth International Symposium on High Performance Computer Architecture (Las Vegas, Nevada), February 1998. Abstract (with BibTex citation), PostScript (1,289k, 20 pages), PDF (218k, 20 pages). David R. O'Hallaron and Jonathan Richard Shewchuk,Properties of a Family of Parallel Finite Element Simulations, Technical Report CMU-CS-96-141, School of Computer Science, Carnegie Mellon University, Pittsburgh, Pennsylvania, December 1996. Abstract (with BibTex citation), PostScript (987k, 22 pages).
David R. O'Hallaron and Jonathan Richard Shewchuk,Properties of a Family of Parallel Finite Element Simulations, Technical Report CMU-CS-96-141, School of Computer Science, Carnegie Mellon University, Pittsburgh, Pennsylvania, December 1996. Abstract (with BibTex citation), PostScript (987k, 22 pages).
Route Planning
HERE, WE APPLY CONFORMING DELAUNAY TRIANGULATIONSto the AI problem of route planning on real-world maps. The problem is inherently “dirty,” with difficulties ranging from one-way streets to incorrect maps, so it is not straightforward even to formally specify a problem to solve. Our approach is to use an analogical planner, which uses past experiences to help choose the best result for future travel. However, this case-based reasoning approach to planning requires a similarity metric to decide which previous cases are most appropriate for the current problem. Our similarity metric begins by describing a geometric problem that roughly approximates the problem of discovering good previous cases, then we solve the geometric problem with a combination of geometric theory and heuristics. The solution of the geometric problem is then cast into an approximate solution to the planning problem, and the rough edges are smoothed by brute-force symbolic planning. This procedure proves to be faster than brute-force symbolic planning from scratch.
 Karen Zita Haigh, Jonathan Richard Shewchuk, and Manuela M. Veloso,Exploiting Domain Geometry in Analogical Route Planning, Journal of Experimental and Theoretical Artificial Intelligence9(4):509–541, October 1997. Abstract, PostScript (1,419k, 30 pages), PDF (688k, 30 pages).
Karen Zita Haigh, Jonathan Richard Shewchuk, and Manuela M. Veloso,Exploiting Domain Geometry in Analogical Route Planning, Journal of Experimental and Theoretical Artificial Intelligence9(4):509–541, October 1997. Abstract, PostScript (1,419k, 30 pages), PDF (688k, 30 pages).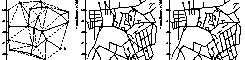 Karen Zita Haigh, Jonathan Richard Shewchuk, and Manuela M. Veloso,Route Planning and Learning from Execution, Working notes from the AAAI Fall Symposium “Planning and Learning: On to Real Applications” (New Orleans, Louisiana), pages 58–64, AAAI Press, November 1994. Abstract, PostScript (163k, 7 pages), PDF (106k, 7 pages). Superseded by the first paper in this list.
Karen Zita Haigh, Jonathan Richard Shewchuk, and Manuela M. Veloso,Route Planning and Learning from Execution, Working notes from the AAAI Fall Symposium “Planning and Learning: On to Real Applications” (New Orleans, Louisiana), pages 58–64, AAAI Press, November 1994. Abstract, PostScript (163k, 7 pages), PDF (106k, 7 pages). Superseded by the first paper in this list.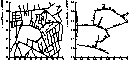 Karen Zita Haigh and Jonathan Richard Shewchuk,Geometric Similarity Metrics for Case-Based Reasoning, Case-Based Reasoning: Working Notes from the AAAI-94 Workshop (Seattle, Washington), pages 182–187, AAAI Press, August 1994. Abstract, PostScript (156k, 6 pages). Superseded by the first paper in this list.
Karen Zita Haigh and Jonathan Richard Shewchuk,Geometric Similarity Metrics for Case-Based Reasoning, Case-Based Reasoning: Working Notes from the AAAI-94 Workshop (Seattle, Washington), pages 182–187, AAAI Press, August 1994. Abstract, PostScript (156k, 6 pages). Superseded by the first paper in this list.