Quick Sort (original) (raw)

Last Updated : 17 Apr, 2025

Try it on GfG Practice

**QuickSort is a sorting algorithm based on the Divide and Conquer that picks an element as a pivot and partitions the given array around the picked pivot by placing the pivot in its correct position in the sorted array.

It works on the principle of **divide and conquer, breaking down the problem into smaller sub-problems.

There are mainly three steps in the algorithm:

1. **Choose a Pivot: Select an element from the array as the pivot. The choice of pivot can vary (e.g., first element, last element, random element, or median).
2. **Partition the Array: Rearrange the array around the pivot. After partitioning, all elements smaller than the pivot will be on its left, and all elements greater than the pivot will be on its right. The pivot is then in its correct position, and we obtain the index of the pivot.
3. **Recursively Call: Recursively apply the same process to the two partitioned sub-arrays (left and right of the pivot).
4. **Base Case: The recursion stops when there is only one element left in the sub-array, as a single element is already sorted.

Here’s a basic overview of how the QuickSort algorithm works.

Choice of Pivot

There are many different choices for picking pivots.

• Always pick the first (or last) element as a pivot. The below implementation picks the last element as pivot. The problem with this approach is it ends up in the worst case when array is already sorted.
• Pick a random element as a pivot. This is a preferred approach because it does not have a pattern for which the worst case happens.
• Pick the median element is pivot. This is an ideal approach in terms of time complexity as we can find median in linear time and the partition function will always divide the input array into two halves. But it takes more time on average as median finding has high constants.

Partition Algorithm

The key process in **quickSort is a partition(). There are three common algorithms to partition. All these algorithms have O(n) time complexity.

1. **Naive Partition: Here we create copy of the array. First put all smaller elements and then all greater. Finally we copy the temporary array back to original array. This requires O(n) extra space.
2. **Lomuto Partition: We have used this partition in this article. This is a simple algorithm, we keep track of index of smaller elements and keep swapping. We have used it here in this article because of its simplicity.
3. **Hoare's Partition: This is the fastest of all. Here we traverse array from both sides and keep swapping greater element on left with smaller on right while the array is not partitioned. Please refer Hoare’s vs Lomuto for details.

Working of Lomuto Partition Algorithm with Illustration

The logic is simple, we start from the leftmost element and keep track of the index of smaller (or equal) elements as **i . While traversing, if we find a smaller element, we swap the current element with **arr[i]. Otherwise, we ignore the current element.

Let us understand the working of partition algorithm with the help of the following example:

**Illustration of QuickSort Algorithm

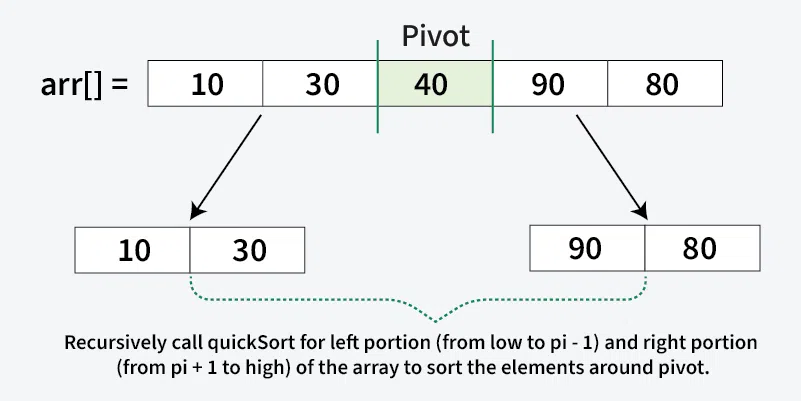
In the previous step, we looked at how the partitioning process rearranges the array based on the chosen **pivot. Next, we apply the same method recursively to the smaller sub-arrays on the **left and **right of the pivot. Each time, we select new pivots and partition the arrays again. This process continues until only one element is left, which is always sorted. Once every element is in its correct position, the entire array is sorted.

Below image illustrates, how the recursive method calls for the smaller sub-arrays on the **left and **right of the **pivot:

**Quick Sort is a crucial algorithm in the industry, but there are other sorting algorithms that may be more optimal in different cases.

C++ `

#include <bits/stdc++.h> using namespace std;

int partition(vector& arr, int low, int high) {

// Choose the pivot
int pivot = arr[high];

// Index of smaller element and indicates 
// the right position of pivot found so far
int i = low - 1;

// Traverse arr[low..high] and move all smaller
// elements on left side. Elements from low to 
// i are smaller after every iteration
for (int j = low; j <= high - 1; j++) {
    if (arr[j] < pivot) {
        i++;
        swap(arr[i], arr[j]);
    }
}

// Move pivot after smaller elements and
// return its position
swap(arr[i + 1], arr[high]);  
return i + 1;

}

// The QuickSort function implementation void quickSort(vector& arr, int low, int high) {

if (low < high) {
  
    // pi is the partition return index of pivot
    int pi = partition(arr, low, high);

    // Recursion calls for smaller elements
    // and greater or equals elements
    quickSort(arr, low, pi - 1);
    quickSort(arr, pi + 1, high);
}

}

int main() { vector arr = {10, 7, 8, 9, 1, 5}; int n = arr.size(); quickSort(arr, 0, n - 1);

for (int i = 0; i < n; i++) {
    cout << arr[i] << " ";
}
return 0;

}

C

#include <stdio.h>

void swap(int* a, int* b);

// Partition function int partition(int arr[], int low, int high) {

// Choose the pivot
int pivot = arr[high];

// Index of smaller element and indicates 
// the right position of pivot found so far
int i = low - 1;

// Traverse arr[low..high] and move all smaller
// elements to the left side. Elements from low to 
// i are smaller after every iteration
for (int j = low; j <= high - 1; j++) {
    if (arr[j] < pivot) {
        i++;
        swap(&arr[i], &arr[j]);
    }
}

// Move pivot after smaller elements and
// return its position
swap(&arr[i + 1], &arr[high]);  
return i + 1;

}

// The QuickSort function implementation void quickSort(int arr[], int low, int high) { if (low < high) {

    // pi is the partition return index of pivot
    int pi = partition(arr, low, high);

    // Recursion calls for smaller elements
    // and greater or equals elements
    quickSort(arr, low, pi - 1);
    quickSort(arr, pi + 1, high);
}

}

void swap(int* a, int* b) { int t = *a; *a = *b; *b = t; }

int main() { int arr[] = {10, 7, 8, 9, 1, 5}; int n = sizeof(arr) / sizeof(arr[0]);

quickSort(arr, 0, n - 1);
for (int i = 0; i < n; i++) {
    printf("%d ", arr[i]);
}

return 0;

}

Java

import java.util.Arrays;

class GfG {

// Partition function
static int partition(int[] arr, int low, int high) {
    
    // Choose the pivot
    int pivot = arr[high];
    
    // Index of smaller element and indicates 
    // the right position of pivot found so far
    int i = low - 1;

    // Traverse arr[low..high] and move all smaller
    // elements to the left side. Elements from low to 
    // i are smaller after every iteration
    for (int j = low; j <= high - 1; j++) {
        if (arr[j] < pivot) {
            i++;
            swap(arr, i, j);
        }
    }
    
    // Move pivot after smaller elements and
    // return its position
    swap(arr, i + 1, high);  
    return i + 1;
}

// Swap function
static void swap(int[] arr, int i, int j) {
    int temp = arr[i];
    arr[i] = arr[j];
    arr[j] = temp;
}

// The QuickSort function implementation
static void quickSort(int[] arr, int low, int high) {
    if (low < high) {
        
        // pi is the partition return index of pivot
        int pi = partition(arr, low, high);

        // Recursion calls for smaller elements
        // and greater or equals elements
        quickSort(arr, low, pi - 1);
        quickSort(arr, pi + 1, high);
    }
}

public static void main(String[] args) {
    int[] arr = {10, 7, 8, 9, 1, 5};
    int n = arr.length;
  
    quickSort(arr, 0, n - 1);
    
    for (int val : arr) {
        System.out.print(val + " ");  
    }
}

}

Python

Partition function

def partition(arr, low, high):

# Choose the pivot
pivot = arr[high]

# Index of smaller element and indicates 
# the right position of pivot found so far
i = low - 1

# Traverse arr[low..high] and move all smaller
# elements to the left side. Elements from low to 
# i are smaller after every iteration
for j in range(low, high):
    if arr[j] < pivot:
        i += 1
        swap(arr, i, j)

# Move pivot after smaller elements and
# return its position
swap(arr, i + 1, high)
return i + 1

Swap function

def swap(arr, i, j): arr[i], arr[j] = arr[j], arr[i]

The QuickSort function implementation

def quickSort(arr, low, high): if low < high:

    # pi is the partition return index of pivot
    pi = partition(arr, low, high)
    
    # Recursion calls for smaller elements
    # and greater or equals elements
    quickSort(arr, low, pi - 1)
    quickSort(arr, pi + 1, high)

Main driver code

if name == "main": arr = [10, 7, 8, 9, 1, 5] n = len(arr)

quickSort(arr, 0, n - 1)

for val in arr:
    print(val, end=" ") 

C#

using System;

class GfG {

// Partition function
static int Partition(int[] arr, int low, int high) {
    
    // Choose the pivot
    int pivot = arr[high];
    
    // Index of smaller element and indicates 
    // the right position of pivot found so far
    int i = low - 1;

    // Traverse arr[low..high] and move all smaller
    // elements to the left side. Elements from low to 
    // i are smaller after every iteration
    for (int j = low; j <= high - 1; j++) {
        if (arr[j] < pivot) {
            i++;
            Swap(arr, i, j);
        }
    }
    
    // Move pivot after smaller elements and
    // return its position
    Swap(arr, i + 1, high);  
    return i + 1;
}

// Swap function
static void Swap(int[] arr, int i, int j) {
    int temp = arr[i];
    arr[i] = arr[j];
    arr[j] = temp;
}

// The QuickSort function implementation
static void QuickSort(int[] arr, int low, int high) {
    if (low < high) {
        
        // pi is the partition return index of pivot
        int pi = Partition(arr, low, high);

        // Recursion calls for smaller elements
        // and greater or equals elements
        QuickSort(arr, low, pi - 1);
        QuickSort(arr, pi + 1, high);
    }
}

static void Main(string[] args) {
    int[] arr = {10, 7, 8, 9, 1, 5};
    int n = arr.Length;

    QuickSort(arr, 0, n - 1);
    foreach (int val in arr) {
        Console.Write(val + " "); 
    }
}

}

JavaScript

// Partition function function partition(arr, low, high) {

// Choose the pivot
let pivot = arr[high];

// Index of smaller element and indicates
// the right position of pivot found so far
let i = low - 1;

// Traverse arr[low..high] and move all smaller
// elements to the left side. Elements from low to
// i are smaller after every iteration
for (let j = low; j <= high - 1; j++) {
    if (arr[j] < pivot) {
        i++;
        swap(arr, i, j);
    }
}

// Move pivot after smaller elements and
// return its position
swap(arr, i + 1, high);
return i + 1;

}

// Swap function function swap(arr, i, j) { let temp = arr[i]; arr[i] = arr[j]; arr[j] = temp; }

// The QuickSort function implementation function quickSort(arr, low, high) { if (low < high) {

    // pi is the partition return index of pivot
    let pi = partition(arr, low, high);

    // Recursion calls for smaller elements
    // and greater or equals elements
    quickSort(arr, low, pi - 1);
    quickSort(arr, pi + 1, high);
}

}

// Main driver code let arr = [ 10, 7, 8, 9, 1, 5 ]; let n = arr.length;

// Call QuickSort on the entire array quickSort(arr, 0, n - 1); for (let i = 0; i < arr.length; i++) { console.log(arr[i] + " "); }

PHP

`

Output

Sorted Array 1 5 7 8 9 10

Complexity Analysis of Quick Sort

**Time Complexity:

• **Best Case: (Ω(n log n)), Occurs when the pivot element divides the array into two equal halves.
• **Average Case (θ(n log n)), On average, the pivot divides the array into two parts, but not necessarily equal.
• **Worst Case: (O(n²)), Occurs when the smallest or largest element is always chosen as the pivot (e.g., sorted arrays).

**Auxiliary Space: O(n),due torecursive call stack

Please refer Time and Space Complexity Analysis of Quick Sort for more details.

Advantages of Quick Sort

• It is a divide-and-conquer algorithm that makes it easier to solve problems.
• It is efficient on large data sets.
• It has a low overhead, as it only requires a small amount of memory to function.
• It is Cache Friendly as we work on the same array to sort and do not copy data to any auxiliary array.
• Fastest general purpose algorithm for large data when stability is not required.
• It is **tail recursive and hence all the tail call optimization can be done.

Disadvantages of Quick Sort

• It has a worst-case time complexity of O(n2), which occurs when the pivot is chosen poorly.
• It is not a good choice for small data sets.
• It is not a stable sort, meaning that if two elements have the same key, their relative order will not be preserved in the sorted output in case of quick sort, because here we are swapping elements according to the pivot's position (without considering their original positions).

**Applications of Quick Sort

Please refer Application of Quicksort for more details.