The Geometry Junkyard: Rectilinear Geometry (original) (raw)

This includes geometric problems defined on squares and rectangles, higher dimensional boxes, cubes, and hypercubes, right triangles and other right-angled figures, and "taxicab geometry" in which distances are measured in terms of axis-parallel paths.

• Acute square triangulation. Can one partition the square into triangles with all angles acute? How many triangles are needed, and what is the best angle bound possible?
  
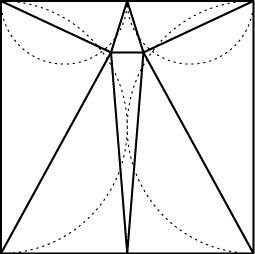
• Animated proof of the Pythagorean theorem, M. D. Meyerson, US Naval Academy.
• Antipodes. Jim Propp asks whether the two farthest apart points, as measured by surface distance, on a symmetric convex body must be opposite each other on the body. Apparently this is open even for rectangular boxes.
• An aperiodic set of Wang cubes, J. UCS 1:10 (1995). Culik and Kari describe how to increase the dimension of sets of aperiodic tilings, turning a 13-square set of tiles into a 21-cube set.
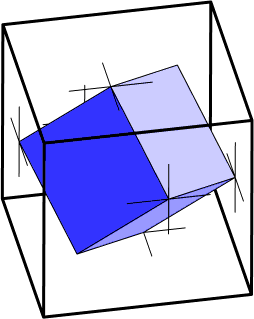
• Box in a box. What is the smallest cube that can be put inside another cube touching all its faces? There is a simple solution, but it seems difficult to prove its correctness. The solution and proof are even prettier in four dimensions.
  
• Calabi's triangle constant, defining the unique non-equilateral triangle with three equally large inscribed squares. Is there a three-dimensional analogue? From MathSoft's favorite constants pages.
• Circular quadrilaterals. Bill Taylor notes that if one connects the opposite midpoints of a partition of the circle into four chords, the two line segments you get are at right angles. Geoff Bailey supplies an elegant proof.
• Covering points by rectangles. Stan Shebs discusses the problem of finding a minimum number of copies of a given rectangle that will cover all points in some set, and mentions an application to a computer strategy game. This is NP-hard, but I don't know how easy it is to approximate; most related work I know of is on optimizing the rectangle size for a cover by a fixed number of rectangles.
• CSE logo. This java applet allows interactive control of a rotating collection of cubes.
• Cube Dissection. How many smaller cubes can one divide a cube into? From Eric Weisstein's treasure trove of mathematics.
• Cube triangulation. Can one divide a cube into congruent and disjoint tetrahedra? And without the congruence assumption, how many higher dimensional simplices are needed to triangulate a hypercube? For more on this last problem, seeTriangulating an n-dimensional cube, S. Finch, MathSoft, andAsymptotically efficient triangulations of the d-cube, Orden and Santos.
  
• DeVicci's Tesseract. Higher-dimensional generalizations of Prince Rupert's cube, from MathSoft's favorite constants pages.
• Distances on the surface of a rectangular box, illustrated using colored wavefronts in this Java applet by Henry Bottomley.
• Distinct point set with the same distance multiset. From K. S. Brown's Math Pages.
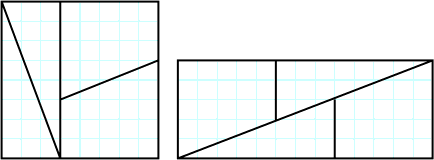
• Fake dissection. An 8x8 (64 unit) square is cut into pieces which (seemingly) can be rearranged to form a 5x13 (65 unit) rectangle. Where did the extra unit come from? Jim Propp asks about possible three-dimensional generalizations.Greg Frederickson supplies one. See alsoAlexander Bogomolny's dissection of a 9x11 rectangle into a 10x10 square andFibonacci bamboozlement applet.
  
• Four dice hypercube visualization.
• Golden rectangles, Curtis McMullen.
• How to construct a golden rectangle, K. Wiedman.
• Hypercube fun. John Atkeson finds a nice recursive drawing pattern for high dimensional hypercubes in two dimensional planes.
• Hypercube game. Experience the fourth dimension with an interactive, stereoscopic java animation of the hypercube.
• Hypercube visualization, Drew Olbrich.
• Hypercubes in hyper perspective. Red-blue 3d visualizations produced with the virtual flower system.
• Intersecting cube diagonals. Mark McConnell asks for a proof that, if a convex polyhedron combinatorially equivalent to a cube has three of the four body diagonals meeting at a point, then the fourth one meets there as well. There is apparently some connection to toric varieties.
• Keller's cube-tiling conjecture is false in high dimensions, J. Lagarias and P. Shor, Bull. AMS 27 (1992). Constructs a tiling of ten-dimensional space by unit hypercubes no two of which meet face-to-face, contradicting aconjecture of Kellerthat any tiling included two face-to-face cubes.
• Richard Kenyon's Gallery of tilings by squares and equilateral triangles of varying sizes.
• Knight's tour art, Dan Thomasson.
• Maximum area cross-section of a hypercube.
• N-dimensional cubes, J. Bowen, Oxford.
• No cubed cube. David Moews offers a cute proof that no cube can be divided into smaller cubes, all different.
• Nonorthogonal polyhedra built from rectangles. Melody Donoso and Joe O'Rourke answer an open question of Biedl, Lubiw, and Sun.
  
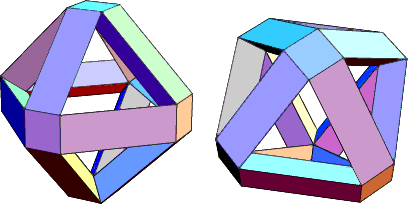
• Orthogonal discrete knots. Hew Wolff asks questions about the minimum total length, or the minimum volume of a rectangular box, needed to form different knots as three-dimensional polygons using only integer-length axis-parallel edges.
• Packing rectangles into similar rectangles. A problem of the month from Erich Friedman's Math Magic site: how small an aspect-ratio-r rectangle can contain n unit-area aspect-ratio-r rectangles? As you might hope for in a problem dealing with aspect ratios of rectangles, the golden rectangle does show up, as one of the breakpoints in the size function for packing five smaller rectangles.
• The Partridge Puzzle. Dissect an (n choose 2)x(n choose 2) square into 1 1x1 square, 2 2x2 squares, etc. The 30-60-90 triangle version of the puzzle is also interesting
• Pi squared by six rectangle dissected into unequal integer squares (or an approximation thereof) by Clive Tooth.
• Pick's Theorem. Mark Dominus explains the formula for area of polygons with vertices in an integer grid.
• Polyominoes, figures formed from subsets of the square lattice tiling of the plane. Interesting problems associated with these shapes include finding all of them, determining which ones tile the plane, and dissecting rectangles or other shapes into sets of them. Also includes related material on polyiamonds, polyhexes, and animals.
• Prince Rupert's Cube. It's possible to push a larger cube through a hole drilled into a smaller cube. How much larger? 1.06065... From Eric Weisstein's treasure trove of mathematics.
• Pythagorean tilings. William Heierman asks about dissections of rectangles into dissimilar integer-sided right triangles.
• Rational square. David Turner shows that a rectangle can only be dissected into finitely many squares if its sides are in a rational proportion.
• Rational triangles. This well known problem asks whether there exists a triangle with the side lengths, medians, altitudes, and area all rational numbers. Randall Rathbun provides some "near misses" -- triangles in which most but not all of these quantities are irrational. See also Dan Asimov's question in geometry.puzzlesabout integer right-angled tetrahedra.
• Rectangles divided into (mostly) unequal squares, R. W. Gosper.
• Rectangular cartograms: the game. Change the shape of rectangles (without changing their area) and group them into larger rectangular and L-shaped units to fit them into a given frame. Bettina Speckmann, TUE. Requires a browser with support for Java SE 6.
• Rotating 4-cube applet, Bernd Grave Jakobi. For the German-challenged, Drehen starts the rotation and the other controls change the axis and speed of rotation.
• Rubik's hypercube. 3x3x3x3 times as much puzzlement. Windows software from Melinda Green and Don Hatch, now also available as Linux executable and C++ source.
• Soap films and grid walks, Ivar Peterson. A discussion of Steiner tree problems in rectilinear geometry.
• Split square. How to subdivide a square into two rectangular pieces, one of which circumscribes the other?
  
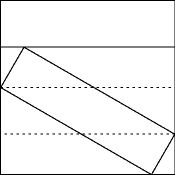
• Squared squares and squared rectangles, thorough catalog by Stuart Anderson.Erich Friedman discusses several related problems on squared squares:if one divides a square into k smaller squares, how big can one make the smallest square? How small can one make the biggest square? How few copies of the same size square can one use? See alsoRobert Harley's four-colored squared square,Mathworld's perfect square dissection page, aGeometry Forum problem of the week on squared squares,Keith Burnett's perfect square dissection page, and Bob Newman's squared square drawing.
• Squares on a Jordan curve. Various people discuss the open problem of whether any Jordan curve in the plane contains four points forming the vertices of a square, and the related but not open problem of how to place a square table level on a hilltop. This is also in thegeometry.puzzles archive.
• Tesseractandtesseract-embedded Möbius strip, A. Bogomolny.
• Three cubes to one. Calydon asks whether nine pieces is optimal for this dissection problem.
• Tic tac toe theorem. Bill Taylor describes a construction of a warped tic tac toe board from a given convex quadrilateral, and asks for a proof that the middle quadrilateral has area 1/9 the original. Apparently this is not even worth a chocolate fish.
• Tiling a rectangle with the fewest squares. R. Kenyon shows that any dissection of a p*q rectangle into squares (where p and q are integers in lowest terms) must use at least log p pieces.
• Tiling the unit square with rectangles. Erich Friedman shows that the 5/6 by 5/6 square can always be tiled with 1/(k+1) by 1/(k+1) squares. Will all the 1/k by 1/(k+1) rectangles, for _k_>0, fit together in a unit square? Note that the sum of the rectangle areas is 1. Marc Paulhus can fit them into a square of side 1.000000001: "An algorithm for packing squares", J. Comb. Th. A 82 (1998) 147-157,MR1620857.
• Tilings. Lecture notes from the Clay Math Institute, by Richard Stanley and Federico Ardila, discussing polyomino tilings, coloring arguments for proving the nonexistence of tilings, counting how many tilings a region has, the arctic circle theorem for domino tilings of diamonds, tiling the unit square with unit-fraction rectangles, symmetry groups, penrose tilings, and more. In only 21 pages, including the annotated bibliography. A nice but necessarily concise introduction to the subject. (Via Andrei Lopatenko.)
• Triangles and squares. Slides from a talk I gave relating a simple 2d puzzle, Escher's drawings of 3d polyhedra, and the combinatorics of 4d polytopes, via angles in hyperbolic space. Warning: very large file (~8Mb). For more technical details seemy paper with Kuperberg and Ziegler.
  
• Visualizations of 4d hypercube (Java applet).
• Whimsical rendering of a 4-cube. Rick Mabry animates a 3d projection that has a nice symmetrical 2d projection.
• Frank Zubek's Elusive Cube. Magnetic tetrahedra connect to form dissections of cubes and many other shapes.

From the Geometry Junkyard, computational and recreational geometry pointers.
Send email if you know of an appropriate page not listed here.
David Eppstein,Theory Group,ICS,UC Irvine.
Semi-automaticallyfilteredfrom a common source file.