Derivation of Formula for Radius of Circumcircle (original) (raw)
The formula for the radius of the circle circumscribed about a triangle (circumcircle) is given by
R=dfracabc4AtR = \dfrac{abc}{4A_t}R=dfracabc4At
where At is the area of the inscribed triangle.
Derivation: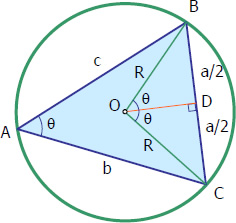 If you have some questions about the angle θ shown in the figure above, see the relationship between inscribed and central angles.
If you have some questions about the angle θ shown in the figure above, see the relationship between inscribed and central angles.
From triangle BDO sintheta=dfraca/2R\sin \theta = \dfrac{a/2}{R}sintheta=dfraca/2R sintheta=dfraca2R\sin \theta = \dfrac{a}{2R}sintheta=dfraca2R
At = area of triangle ABC At=frac12bcsinthetaA_t = \frac{1}{2}bc \sin \thetaAt=frac12bcsintheta At=frac12bcleft(dfraca2Rright)A_t = \frac{1}{2}bc \left( \dfrac{a}{2R} \right)At=frac12bcleft(dfraca2Rright) At=dfracabc4RA_t = \dfrac{abc}{4R}At=dfracabc4R R=dfracabc4AtR = \dfrac{abc}{4A_t}R=dfracabc4At