Brachistochrone (original) (raw)
| next curve | previous curve | 2D curves | 3D curves | surfaces | fractals | polyhedra |
|---|
BRACHISTOCHRONE CURVE
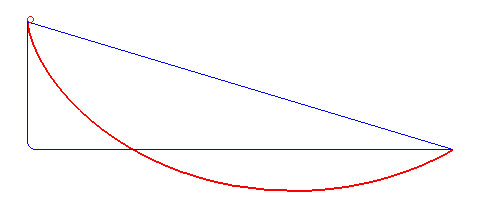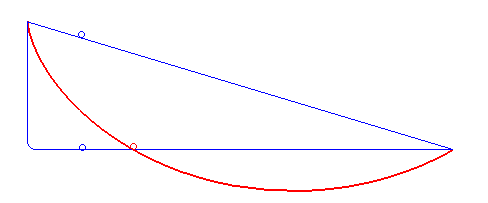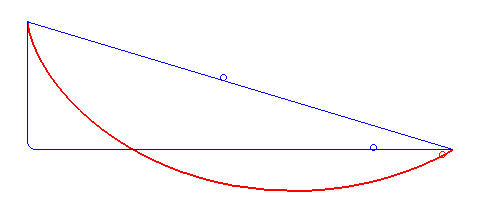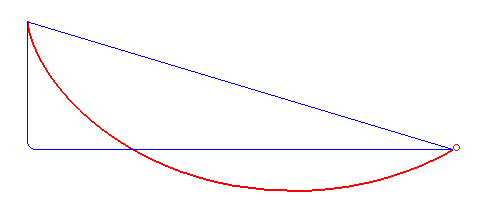
The brachistochrone (curve) is the curve on which a massive point without initial speed must slide without friction in an uniform gravitational field in such manner that the travel time is minimal among all the curves joining two fixed points O and A (here_A_(a,-b)).
Solution for a > 0 (result found at the same time by Leibniz, Newton, L'Hospital, Jean and Jacques Bernoulli): an arc of a cycloid starting with a vertical tangent.
It can be noted that if the slope b/a between_O_and A is less than 2/p »63%, corresponding to an angle of »32 ° with the horizontal, the fastest curve has, as in the figure above, a portion that goes upwards!
This is valid in the limit when the points O and_A_are at the same altitude, in which case the straight line would have an infinite travel time.
| Here the two balls are side by side for a while, then the blue one follows a straight horizontal line. The cycloid is still the fastest! Animation dedicated to editorial board of the TV show "incredible experiments" on France 2 that struggles to accept this phenomenon... |  |
|---|---|
| The way Jean Bernoulli posed the problem was slightly different: find the curve minimising the travel time from a point O, without initial speed, to a vertical plane (at an indefinite point). The solution is half an arch of a cycloid with a vertical start and horizontal end, perpendicular to the plane. At the end point, the moving body's altitude decreased by |
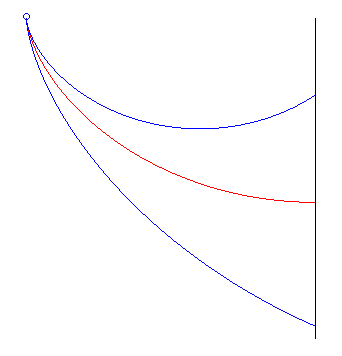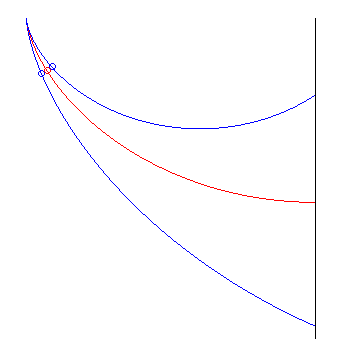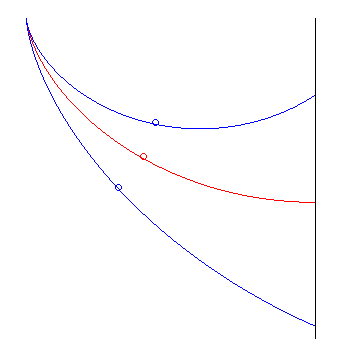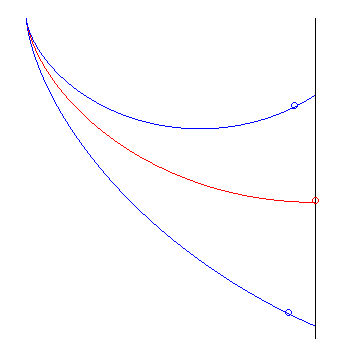 the red cycloid beats the other two the red cycloid beats the other two |
| It can also be asked what the brachistochrone curve among the curves joining two points and having a given shape would be. For example, for two points at the same altitude and V-shaped curves, the brachistochrone curve is the one for which the angle of the V is a right angle, as is shown in the animation opposite. This example also shows that among all the linear paths starting at a given point A and ending on a given vertical plane_P_, the brachistochrone is the one making a 45° angle with the horizontal and that is traced in the vertical plane passing through A and orthogonal to P (result obtained by Galileo in 1638). The problem of the brachistochrone _with given length_is studied on this page. | 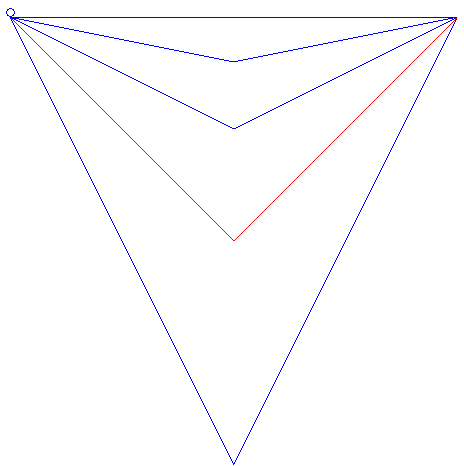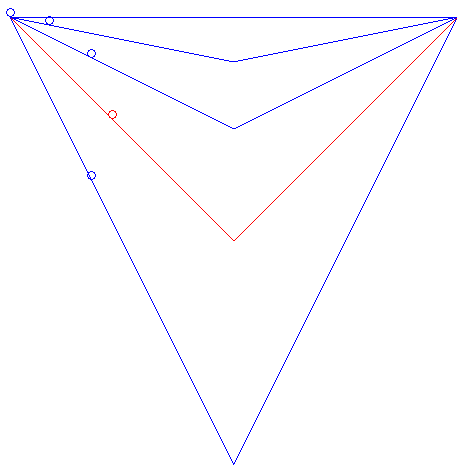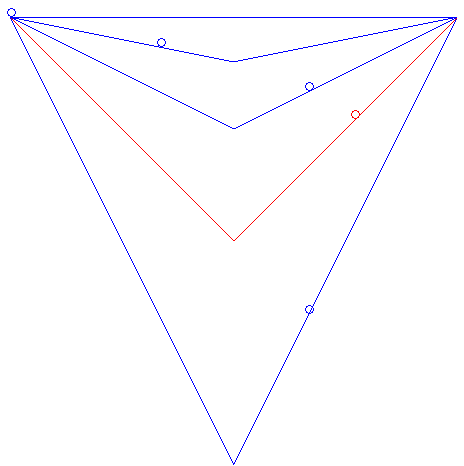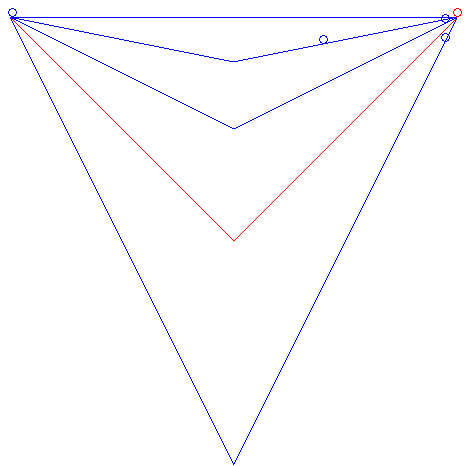 |
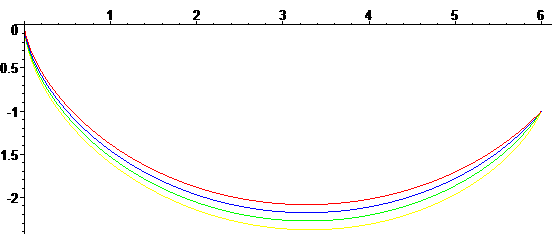
| One can also try to find the brachistochrone "with friction". We get the parametrization |
 |
 |
|---|
Generalisations:
We can consider the brachistochrone curves traced on surfaces.
We can also look for the brachistochrone curves obtained for various speed laws.
Here , but for the more general case
, the differential equation of the brachistochrone is
.
If , the brachistochrone we get this time is an arc of a circle.
If now the speed only depends on the distance to O(), the differential equation of the brachistochrone is
.
For , the brachistochrone is the logarithmic spiral ; this case corresponds to a moving body in a reference frame in uniform rotation around O (hence subject to the centrifugal force) when the speed at O is zero.
© Robert FERRÉOL2017