Phenotypic Tolerance: Antibiotic Enrichment of Noninherited Resistance in Bacterial Populations (original) (raw)

Abstract

When growing bacteria are exposed to bactericidal concentrations of antibiotics, the sensitivity of the bacteria to the antibiotic commonly decreases with time, and substantial fractions of the bacteria survive. Using Escherichia coli CAB1 and antibiotics of five different classes (ampicillin, ciprofloxacin, rifampin, streptomycin, and tetracycline), we examine the details of this phenomenon and, with the aid of mathematical models, develop and explore the properties and predictions of three hypotheses that can account for this phenomenon: (i) antibiotic decay, (ii) inherited resistance, and (iii) phenotypic tolerance. Our experiments cause us to reject the first two hypotheses and provide evidence that this phenomenon can be accounted for by the antibiotic-mediated enrichment of subpopulations physiologically tolerant to but genetically susceptible to these antibiotics, phenotypic tolerance. We demonstrate that tolerant subpopulations generated by exposure to one concentration of an antibiotic are also tolerant to higher concentrations of the same antibiotic and can be tolerant to antibiotics of the other four types. Using a mathematical model, we explore the effects of phenotypic tolerance to the microbiological outcome of antibiotic treatment and demonstrate, a priori, that it can have a profound effect on the rate of clearance of the bacteria and under some conditions can prevent clearance that would be achieved in the absence of tolerance.

When dividing bacteria are exposed to bactericidal concentrations of antibiotics, the density of viable cells does not decline exponentially. During exposure to antibiotics, the rate of mortality of bacteria decreases, and a substantial fraction of bacteria may survive and even start to grow again. This decrease in mortality has been observed for virtually all antibiotics used clinically and for many different species of bacteria (7-9, 12, 15-18, 27, 30, 32). We investigate this phenomenon by combining a population dynamic analysis with in vitro experiments.

With the aid of mathematical models, we develop these three hypotheses to account for the decrease in bacterial mortality: (i) antibiotic decay (since the efficacy of antibiotics increases with their concentration, a decay in the effective concentration of the antibiotics leads to a decrease in mortality), (ii) inherited resistance (an ascent of genetically resistant mutants decreases the mortality of the total bacterial population), and (iii) phenotypic tolerance (the bacterial population, though genetically homogeneous, is physiologically heterogeneous with respect to its susceptibility, which during antibiotic exposure leads to an enrichment of the fraction of phenotypically tolerant bacteria and thus a decrease in the overall bacterial mortality).

We investigate this phenomenon in vitro, using Escherichia coli and five classes of antibiotics (ciprofloxacin, ampicillin, rifampin, streptomycin, and tetracycline).

We present evidence against the first two of these hypotheses and in support of the third hypothesis (phenotypic tolerance). Using a mathematical model of antibiotic treatment, we demonstrate that phenotypic tolerance can impair the efficacy of treatment.

MATERIALS AND METHODS

Bacteria.

The majority of the experiments performed were with E. coli O18:K1:H7 (designated CAB1). This pathogenic strain of E. coli was originally isolated from a child with meningitis and supplied by Craig A. Bloch (4, 5). This strain has been used in thigh model experiments of phage and antibiotic treatment (6) and in our earlier studies of the pharmacodynamics of antibiotics (30), and we are using it in our studies of the within-host dynamics of antibiotic treatment. A few experiments were also performed with two strains of E. coli K-12, C600 and MG1655.

We also used variants of E. coli CAB1 resistant to antibiotics. We used spontaneous mutants and transconjugants. Spontaneous mutants that were resistant to nalidixic acid, rifampin, and streptomycin were obtained by plating approximately 2 × 109 E. coli CAB1 from cultures grown overnight onto LB agar with either 64 μg of nalidixic acid per ml, 25 μg of rifampin per ml, or 40 μg of streptomycin per ml. Transconjugants were generated by conjugative transfer of plasmid R1 (Cm, Km, Am, Sm/Sp) and/or plasmid RK2 (Am, Tc) into E. coli CAB1. To test whether the time-kill results observed in this study were restricted to one strain (E. coli CAB1), we repeated these experiments with E. coli K-12 MG1655.

Culture and sampling media.

Bacteria were grown at 37°C with aeration and shaking (200 rpm) in Luria-Bertani (LB) broth (Difco) with 10 ml of broth in 50-ml Erlenmeyer flasks or 50 to 100 ml of broth in 250-ml flasks. Total cell densities and the densities of antibiotic-resistant mutants and transconjugants were estimated from CFU data by diluting the bacteria (in 0.85% saline) and plating on LB agar and LB agar with the selecting antibiotics, respectively.

Antibiotics.

Ciprofloxacin was from Mediatech, Inc. (Herndon, Va.), and ampicillin, rifampin, streptomycin, and tetracycline were from Sigma-Aldrich (St. Louis, Mo.). The stock solution of rifampin (10 mg/ml) was dissolved in methanol, and the stock solution of tetracycline (25 mg/ml) was dissolved in 50% ethanol. The stock solutions of streptomycin, ampicillin, and ciprofloxacin were dissolved in sterile distilled water (at 40, 25, and 10 mg/ml, respectively). The stock solutions of rifampin, ciprofloxacin, and tetracycline were maintained at −20°C, and those of ampicillin and streptomycin were maintained at 4°C.

Antibiotic time-kill curves.

Cultures of E. coli CAB1 grown overnight in LB broth were diluted in 10 ml of fresh warm (37°C) LB broth and incubated for 2 h to initiate exponential growth. These cultures were grown to a final density of approximately 2 × 106 cells per ml before antibiotics were added (dissolved in LB broth). The cultures were incubated with shaking at 200 rpm at 37°C and sampled to estimate the number of CFU per milliliter every 15 min for the first 2 h, every 30 min for the next 2 h, and at 4, 6, and 24 h. Time-kill curves were obtained in each case for two antibiotic concentrations, selected to illustrate the possibility of different concentration-dependent killing dynamics.

Effective concentrations of antibiotics.

Bioassays were used to monitor the changes in the effective concentration of antibiotics. At specific times after the start of the time-kill experiments, the cultures were passed through 0.45-μm-pore-size membrane filters (Tyffryn; Pall Corporation) to remove the bacteria. Aliquots of 0.1 ml of exponentially growing monocultures of E. coli CAB1 or mixed cultures of exponentially growing E. coli CAB1 containing low frequencies of E. coli CAB1 or C600 resistant to the antibiotic in the medium were added to the supernatant and incubated for 2 h at 37°C. Samples were then taken and plated on LB agar with and without the selecting antibiotic to estimate the density of viable cells and the relative frequency of the resistant strain. In the experiments with monocultures, the decline in viable cell density at 2 h was measured in fresh antibiotic-containing medium and in the filtrates of used medium with antibiotics (with new bacteria added). Changes in bactericidal activity were statistically evaluated by paired Wilcoxon signed-rank test using the R program (a P value of less than 0.05 was considered statistically significant). In the experiments with mixed cultures (sensitive and resistant strains), the decline in the viable density of the total population and the increase in the frequency of resistance in the mixed cultures were used as measures of the activity of antibiotics, a resistance competition assay (6).

Tests for resistant mutants. (i) Test for inherited resistance.

Single colonies were tested for mutation to resistance by streaking on LB agar plates containing resistance breakpoint concentrations of streptomycin (40 μg/ml), rifampin (25 μg/ml), and nalidixic acid (30 μg/ml) (i.e., concentrations allowing growth of only resistant mutants).

(ii) MIC estimation by Etest.

Aliquots of 0.2 ml of single-colony cultures grown overnight were spread on LB agar onto which Etest strips (AB Biodisk, Solna, Sweden) were placed. Estimates of the MICs for these cultures were obtained the next day using the Etest criteria.

Reexposure experiments.

At different times in the course of time-kill experiments, 10-ml samples of the cultures were passed through 0.45-μm-pore-size membrane filters and washed with fresh LB broth, and the bacteria on the filters were suspended in LB broth containing different concentrations of either the same or different antibiotics. Samples of the antibiotic-exposed bacteria were obtained during the exponential decline phase (at 30 min) and later at 1.5 and 3 h. For controls, 10-ml samples from exponentially growing cultures with no history of antibiotic exposure were filtered and resuspended in fresh medium with antibiotic. The viable density of cells (in reexposed and control cultures) was determined at time zero when the drug was added and at the end of each reexposure period, at 2 or 3 h. In the experiments in which the cells were reexposed to other antibiotics (the generality experiments) or higher concentrations of the same antibiotic (the robustness experiments), the samples were removed and reexposed at 4 h.

RESULTS

Time-kill curves.

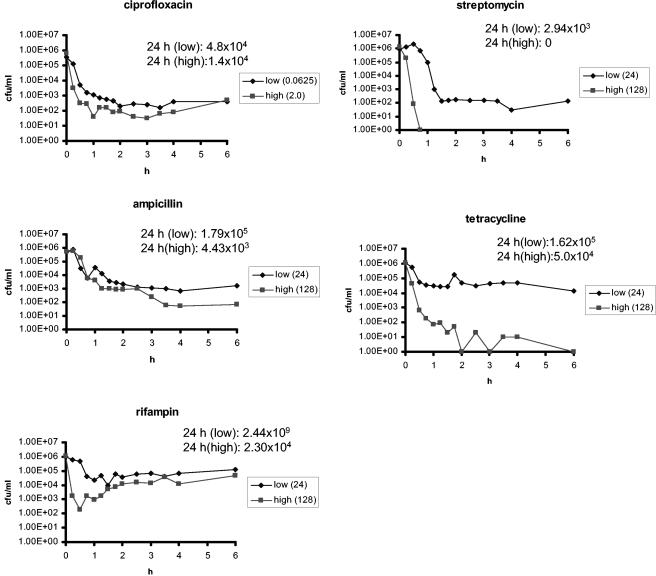
In Fig. 1, we illustrate the phenomenon that motivated the investigation: the decline in the density of viable bacteria over time and the apparent decline in the rate of mortality in time-kill experiments with E. coli CAB1 exposed to two concentrations of antibiotics in five different classes of antibiotics. The time at which the density of viable cells begins to decline and the initial rate of mortality varies among antibiotics and their concentrations. For all five antibiotics, the rate of mortality initially declines, and then, between 1.5 and 2 h of exposure, the number of viable cells from these cultures stays roughly constant. After the period of initial killing, bacteria exposed to streptomycin exhibited a slight decrease in density, and bacteria exposed to rifampin exhibited some regrowth.

FIG. 1.

FIG. 1.

Time-kill curves. Changes in estimated densities of viable E. coli CAB1 (in CFU per milliliter) exposed to ciprofloxacin, ampicillin, rifampin, streptomycin, and tetracycline. The concentrations of the antibiotics (in micrograms per milliliter) are shown in the symbol key boxes. The MICs of these antibiotics for E. coli CAB1 are listed in Table 3.

For a more detailed consideration of the decline in the rate of mortality, the number of viable cells present at different times was determined. Ten independent exponential cultures of E. coli CAB1 were exposed for 24 h to each antibiotic at the lower concentration used in the time-kill experiments in Fig. 1. The densities of viable bacteria at 0, 4, and 24 h are listed in Table 1.

TABLE 1.

Densities of viable bacteria at three different times

Antibiotica MIC (μg/ml) Range of densities of viable bacteriab (CFU/ml) at:
0 h 4 h 24 h
None (control) 3.1 × 105-1.1 × 106 2.8 × 108-6.7 × 108 2.3 × 109-3.6 × 109
CIP 0.008 4.2 × 105-1.0 × 106 2.9 × 103-9.4 × 103 1.0 × 101-1.3 × 104
AMP 1.5 4.2 × 105-1.0 × 106 2.4 × 103-1.1 × 104 0-5.0 × 101c
RIF 8 3.1 × 105-1.1 × 106 1.1 × 103-4.1 × 104 1.0 × 103-8.0 × 103
STR 2 3.1 × 105-1.1 × 106 0-3.7 × 103d 0-8.4 × 108e
TET 2 3.1 × 105-1.1 × 106 1.9 × 104-3.8 × 104 0-7.0 × 103c

With the exception of cultures exposed to streptomycin, there were more than 103 CFU/ml present in the cultures after 4 h of exposure. While the density of viable cells declined during the next 20 h, there were still substantial numbers of viable cells present in the majority of the cultures at 24 h. For cultures exposed to streptomycin, only two cultures had viable cells at 24 h, and one of those reached a density of 109 CFU/ml. Upon testing this culture by plating on LB agar with streptomycin, these cultures proved to be dominated by streptomycin-resistant cells.

To ascertain whether these results were restricted to E. coli CAB1, we performed similar time-kill experiments with E. coli K-12 (MG1655). We obtained analogous results with a decline in the rate of mortality with persistence of a fraction of viable bacteria (data not shown).

Three hypotheses and their predictions by computer simulations.

We consider three hypotheses to account for the decline in the rate of mortality with persistence of a fraction of viable bacteria in the time-kill experiments presented in Fig. 1: (i) decay in the concentration of the antibiotic (as time proceeds, the antibiotic becomes decreasingly bactericidal), (ii) inherited resistance (the population initially includes a minority of genetically resistant cells which increases in number and frequency as the sensitive population dies), and (iii) phenotypic tolerance (there is variation among the bacteria in their susceptibility to the different antibiotics, and as time proceeds, the relative frequency of the more tolerant members of the population increases). To illustrate how these different hypotheses can account for the observations and the predictions they make, we solved differential equation models of each of these processes numerically, the details of which are included in the Appendix. These simulations were programmed by using the Berkeley Madonna program and can be obtained from the www.eclf.net website. For the analysis of the properties of these models, we use parameters that provide initial mortality rates similar to those observed for E. coli CAB1 in vitro (Fig. 1). The parameters are listed in the legend to Fig. 7.

FIG. 7.

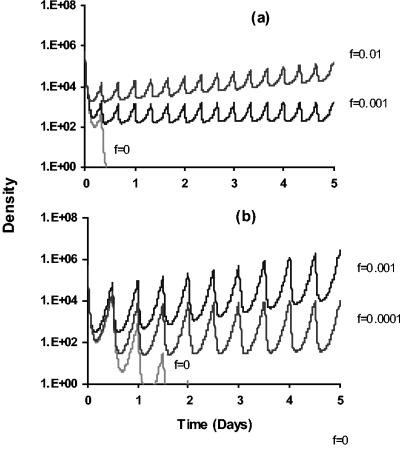
FIG. 7.

Computer simulation of antibiotic treatment with and without tolerance. Changes in the density of viable bacteria with different levels of tolerance and treatment regimens are shown. For pharmacokinetics, the initial concentration of antibiotic is a_0 and decays exponentially with a rate parameter, γ, of 0.5 h−1. At either 8- or 12-h intervals 10 μg of that antibiotic per ml is added. For pharmacodynamics, we assume a Hill function for the pharmacodynamics of the sensitive subpopulation μ_S(a) with ψ_S_max = 1.0 h−1, ψ_S_min = −10.0 h−1, zMIC = 4 μg/ml, and the Hill coefficient κ = 1 (see Appendix). The maximum replication rate of the tolerant subpopulation is ψ_T_max = 0.5 h−1, and the tolerant population is unaffected by the antibiotic. With these parameters, in the absence of antibiotic decay, the time-kill curve for the tolerant population is identical to that in Fig. 2c. (a) Effects of different values of the tolerance parameter, f, and antibiotic dose (10 μg/ml) every 8 h. (b) Effects of different values of the tolerance parameter, f, and antibiotic dose (10 μg/ml) every 12 h.

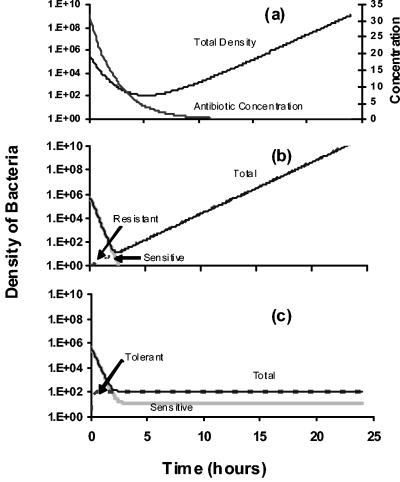
As in the experiments presented in Fig. 1, in these simulations we monitor the dynamics of changes in bacterial density for 24 h. In Fig. 2a, we present the results of a simulation in which the effective concentration of the antibiotic declines exponentially. We assume that the rate of mortality of the bacteria is a function of the concentration of the antibiotic, a Hill function (30). Under these conditions, the rate of mortality of the susceptible population continues to decline as the antibiotic decays. The lower the rate of decay of the effective antibiotic concentration is, the greater the rate of mortality is, and the greater the extent to which the density of viable bacteria declines. Eventually, the effective concentration of the antibiotic falls below the pharmacodynamic MIC (zMIC) of the antibiotic [i.e., the antibiotic concentration that causes ψ(zMIC) = 0], and the bacterial population begins to grow. With the parameters used to generate the simulations in Fig. 2a, the density of viable bacteria at 24 h exceeds 2 × 109 cells/ml. One testable prediction of the antibiotic decay hypothesis is that when the rate of mortality levels off or the population begins to increase, the antibiotic would no longer be bactericidal.

FIG. 2.

FIG. 2.

Computer simulations. Predicted results of time-kill experiments anticipated under the three hypotheses are shown. (A) Antibiotic decay. Rate of antibiotic decay γ = −0.4 h−1. Hill function parameters for the pharmacodynamics follow: maximum and minimum growth rates, ψmax = 1.0 h−1; ψmin = −10.0 h−1; zMIC = 4 μg/ml; Hill coefficient κ = 1. The right x axis is the antibiotic concentration. (B) Inherited resistance. Growth rate of sensitive cells rS = 1; death rate of sensitive cells mS = 6; growth rate of resistant cells rR = 1. The initial density of resistant cells is 1 cell per ml. (C) Phenotypic tolerance. Growth rate of sensitive cells rS = 1; growth rate of tolerant cells rT = 0.5; mortality of sensitive cells mS = 10; death rate of tolerant cells mT = 0; tolerance parameter f = 0.001. The descriptions of these models and the equations used in these simulations are presented in the Appendix.

In the inherited resistance model simulation shown in Fig. 2b, the viable cell density of the sensitive population (S) declines exponentially while that of the resistant population (R) increases exponentially. We assume that initially there is only a single resistant cell. This model makes three related predictions. First, when the mortality rate has declined and the number of viable cells is increasing at a roughly constant rate, the majority of cells should be resistant. Second, unless these resistant bacteria have a severe growth rate disadvantage, the total cell densities at 24 h should approach those anticipated for stationary-phase cultures in antibiotic-free medium. Third, the bacteria that survive initial killing would be genetically resistant and therefore would continue to grow if reexposed to the same antibiotic.

In Fig. 2c, we present the results of simulations of the phenotypic tolerance model. In this model, we assume that the bacteria are of two states, one sensitive to killing by the antibiotic and one tolerant. In contrast to genetic resistance, these states are not inherited; when a new bacterial cell arises, the probability that it will be tolerant (f) is the same for sensitive and tolerant mother cells. We refer to f as the tolerance parameter.

In the parameters used in the simulations presented in Fig. 2c, we assume that the rate at which tolerant cells are produced, f, is substantially less than the rate of production of sensitive cells (1 − f). After addition of antibiotics, the sensitive cells decline exponentially, tolerant cells become enriched, and the rate of mortality of the total population, N, declines. The number of viable cells present when the time-kill curve levels off depends on the tolerance parameter, f. The larger the value of f is, the greater the density of phenotypic tolerant cells will be when the total population reaches a low density. Another prediction of the phenotypic tolerance model is that samples taken during the exponential decline phase would be dominated by sensitive cells while those taken after the rate of mortality has declined would be dominated by tolerant cells.

Tests of the hypotheses by in vitro experiments.

While we believe these three classes of hypotheses are exhaustive, they are not mutually exclusive and could be operating simultaneously.

(i) Recovery of viable cells at 24 h.

In the majority of cases, when cultures containing approximately 106 E. coli CAB1 per ml are exposed to the five antibiotics, the number of viable cells at 24 h is less than 105 CFU/ml (Table 1). This relatively low density of cells at 24 h is inconsistent with the predictions of both the antibiotic decay hypothesis and the inherited resistance hypothesis. Both of these hypotheses predict bacterial densities at 24 h approaching those of stationary-phase cultures (∼109), either because of a decline in bactericidal activity followed by growth of sensitive bacteria or because of growth of genetically resistant cells (assuming these cells do not have too large of a growth disadvantage). Finally, in accord with the inherited resistance hypothesis, it should be possible to recover cells with inherited resistance soon after the total cell density has stopped decreasing. While rifampin-, nalidixic acid-, and streptomycin-resistant mutants were recovered from some exposed cultures, this was a relatively rare outcome in the time-kill experiments and could not account for the majority of these results.

(ii) Effective antibiotic concentration.

We compared the rate of killing of exponentially growing E. coli CAB1 in fresh LB broth with antibiotics (fresh medium) with the rate of killing in 5-h-old cell-free filtrates of previously exposed cultures (filtrates). The results of these experiments are presented in Table 2. For ciprofloxacin, ampicillin, rifampin, and streptomycin, there was either no decline or a small decline in the bactericidal activity, while for tetracycline, the bactericidal activity appeared to be greater in the filtrates than in the fresh medium. None of these differences were statistically significant. We interpret these results to suggest that decay in the effective concentration of the antibiotic could account for some of the decline in the rate of mortality of bacteria exposed to ciprofloxacin and streptomycin but could not account for the decline in mortality of bacteria exposed to ampicillin, rifampin, and tetracycline. After 5 h, all antibiotics tested remained bactericidal.

TABLE 2.

Changes in the bactericidal activity of the antibioticsa

Exposure Average decline in log (CFU/ml) after 2 h of exposure ± SD
CIP (0.0625) AMP (48) RIF (48) STR (32) TET (48)
First exposure 3.6 ± 0.3 3.3 ± 0.3 2.1 ± 0.2 3.7 ± 0.3 2.0 ± 0.4
Second exposure 2.9 ± 0.7 3.2 ± 0.5 2.0 ± 0.8 3.3 ± 0.9 2.9 ± 0.3
P values 0.125 0.5 0.375 0.375 1

The resistance competition assay (6) also suggests that there is little if any decay in the effective concentrations of the antibiotics. When exponentially growing cultures containing mixtures with a minority of resistant bacteria and a majority of sensitive bacteria are exposed in antibiotic-containing filtrates obtained after 3 h of initial exposure, the total number of susceptible bacteria declines while the number of resistant bacteria increases. After 2 h of exposure to the antibiotic-containing filtrates, the viable densities of the total populations declined at least 1 log (CFU/ml). The frequency of resistant cells in these mixtures increased by approximately 100-fold in the cultures exposed to rifampin and streptomycin, 1,000-fold after exposure to ampicillin and tetracycline, and 10,000-fold after exposure to ciprofloxacin. The continued growth of the resistant strain shows that the medium was still able to support the growth of bacteria. While these results are not sufficient to rule out some decay in the effective concentration of the antibiotic, they exclude the possibility that the decline in the rate of mortality in Fig. 1 can be attributed solely to decay in the effective concentration of the antibiotic.

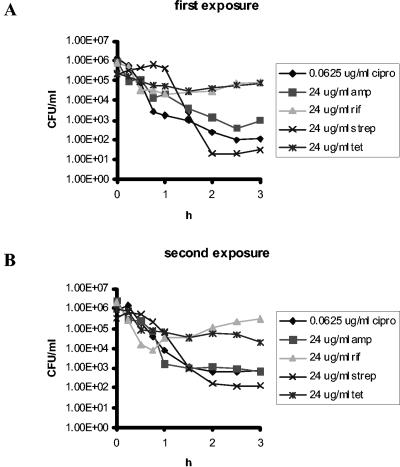
(iii) Time-kill curves of cultures derived from exposed cells.

If inherited resistance were responsible for the decline in the rate of mortality and the survival of bacteria in the presence of antibiotics, the shape of time-kill curves of cultures derived from the survivors of time-kill experiments should be different from those of cultures derived from bacteria that have not been exposed to antibiotics. More specifically, these cultures should be dominated by resistant cells, and there should be little if any decline in the density of the total bacterial population in the presence of antibiotics. However, this was not the case. The trajectories of the time-kill curves produced from cultures of bacteria isolated from bacteria with prior exposure to antibiotics were effectively the same as those derived from cells that had no prior exposure to the antibiotic (Fig. 3).

FIG. 3.

FIG. 3.

Test for inherited resistance in whole cultures. (A) Exposure of whole cultures of naïve E. coli CAB1. (B) Reexposure of cultures surviving 3 h of exposure. The surviving cells from panel A at 3 h were caught on filters and subcultured overnight in the absence of antibiotics before they were reexposed to the same drug. The antibiotic concentrations are shown in micrograms per milliliter. Antibiotic abbreviations: cipro, ciprofloxacin; amp, ampicillin, rif, rifampin; strep, streptomycin; tet, tetracycline.

(iv) Test for inherited resistance in single colonies obtained from exposed culture.

As another test of the inherited resistance hypothesis, we picked single colonies from exposed cultures and subcultured them on LB agar plates with antibiotics. No bacteria resistant to mutant breakpoint concentrations of streptomycin, rifampin, or nalidixic acid were observed in more than 50 colonies in samples taken after 4 h of exposure to these antibiotics (a minimum of two experiments were performed for each antibiotic). While this does not exclude the possibility that there were some genetically resistant bacteria in these cultures, at most they could be only a small minority of the surviving populations.

(v) Test for inherited resistance by Etest.

To ascertain whether there may be inherited resistance to low concentrations of the antibiotics, we used Etest to estimate the MICs of antibiotics for unexposed bacteria and bacteria obtained after 4 h of antibiotic exposure from four independent time-kill experiments. The MICs from these Etests are listed in Table 3. The results of these experiments were also inconsistent with the inherited resistance hypothesis. The MICs of antibiotics for cultures derived from single colonies of bacteria that survived exposure to antibiotics were the same as those derived from unexposed bacteria. Most colonies tested had either no increase or small increases in MIC, but all remained well below the resistance breakpoints.

TABLE 3.

MICs of antibiotics (by Etest) for bacteria that survived exposure to antibioticsa

Antibioticb MICc Change in MIC No. of surviving bacteria at the following MIC (μg/ml):
12 8 6 2 1.5 0.75 0.012 0.008
CIP 0.008 Yes 1 3
AMP 1.5 Yes 3 1
RIF 8 Yes 3 1
STR 2 Yes 3 1
TET 2 No 4

(vi) Tests of the phenotypic tolerance hypothesis. (a) Reexposure experiments.

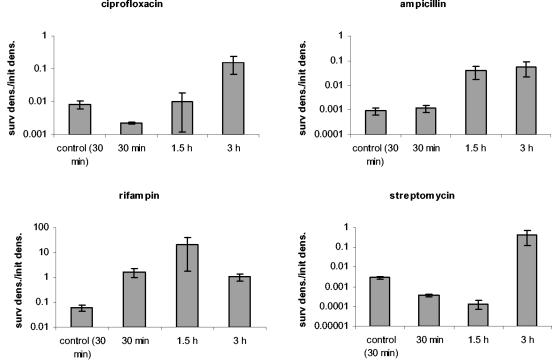
In accord with the phenotypic tolerance hypothesis, unexposed bacteria and bacteria removed during the early phase of a time-kill experiment should be dominated by susceptible cells. When reexposed to that antibiotic in fresh medium, their population should continue to decline at a rapid rate. In contrast, when bacteria removed later in a time-kill experiment are reexposed to antibiotics, they should be killed at a rate lower than that of cells isolated earlier or naïve cells. We tested this hypothesis by taking cells from various stages of the time-kill experiments and reexposing them to the same concentration of the same antibiotic. The results of these experiments are presented in Fig. 4. The results are consistent with the prediction of the phenotypic tolerance hypothesis. When reexposed to ciprofloxacin, ampicillin, and streptomycin, bacteria removed 30 min after initial exposure to these antibiotics die at the same rate or at a rate only slightly lower than that of unexposed controls. When reexposed to rifampin and tetracycline, bacteria isolated at 30 min after exposure to these antibiotics die at a rate substantially less than that of the naïve controls. For all five drugs, when the exposed bacteria were removed at 1.5 and 3 h, the rate of mortality was considerably less than that of the naïve controls. This suggests that the bacteria taken at these times were phenotypically tolerant.

FIG. 4.

FIG. 4.

FIG. 4.

Test for phenotypic tolerance. Reexposure of cells previously exposed to antibiotics for different periods of time (30 min, 1.5 h, and 3 h). Controls were exponentially growing cells with no history of antibiotic exposure. The antibiotic concentrations were as follows: 0.0625 μg/ml for ciprofloxacin and 24 μg/ml for ampicillin, rifampin, streptomycin, and tetracycline. Survival after the reexposure is depicted here. The values represent the log10 ratios of the density of surviving cells after 2 h of exposure and their densities prior to reexposure (surv dens./init dens.). Each value represents the average ratio ± standard error (error bar) of three experiments.

(b) Robustness of the phenotypic tolerance.

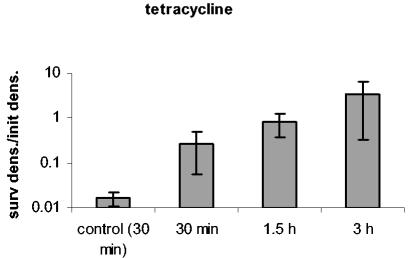
To determine whether the phenotypic tolerance seen during antibiotic exposure is restricted to the concentration to which they were exposed, we exposed bacteria removed from time-kill experiments after 4 h of preexposure to higher concentrations of the same drug. The results of these experiments are presented in Fig. 5. For all five drugs, the bacteria exhibited some tolerance to higher concentrations of the same drug. The extent of tolerance (as measured by the decline in the number of bacteria surviving reexposure relative to that of naïve bacteria) and the length of time of the tolerance period varied among these antibiotics. For tetracycline, bacteria did not exhibit tolerance to 96 μg/ml.

FIG. 5.

FIG. 5.

FIG. 5.

Test for robustness. E. coli CAB1 was exposed to a low concentration of one antibiotic and then reexposed to increasing concentrations of the same antibiotic. Survival after the reexposure is depicted here. Antibiotic concentrations at the first exposure were 0.0625 μg/ml for ciprofloxacin and 24 μg/ml for ampicillin, rifampin, streptomycin, and tetracycline. The bars represent the ratios of the density of surviving cells (after the second exposure) relative to the initial density at reexposure (surv dens/init dens.). The time of reexposure is shown on the x axis. The boxed control values are the ratios of the density of surviving naïve cells after 2 h of exposure relative to the initial density. The concentrations of the antibiotics (in micrograms per milliliter) at the second exposure are noted in the symbol key boxes.

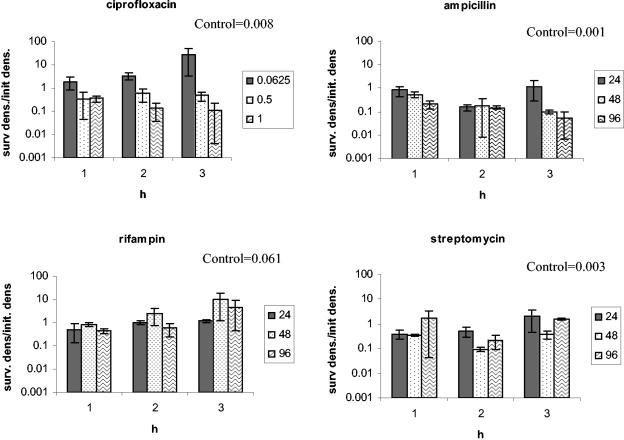
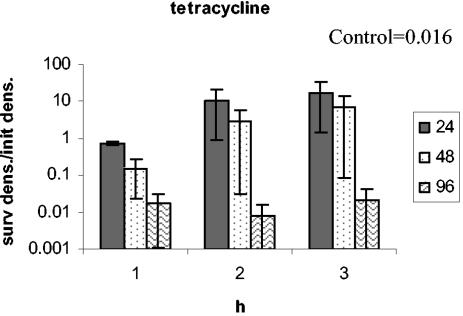
(c) Test of the generality of the phenotypic tolerance.

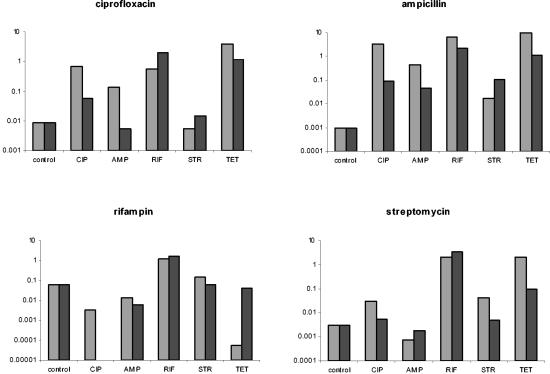
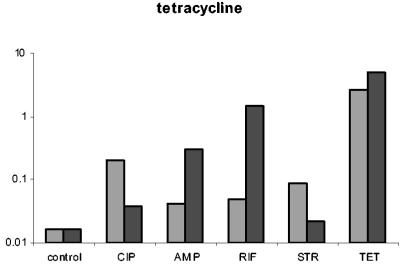
To ascertain whether exposure to one antibiotic renders bacteria tolerant to antibiotics of different classes (cross-tolerance), cultures were exposed for 4 h to one class of antibiotic and then reexposed to a different antibiotic. We assumed cross-tolerance occurred when the number of bacteria recovered after reexposure to another drug was the same (or greater) than after reexposure to the same drug. The results of these experiments are presented in Fig. 6.

FIG. 6.

FIG. 6.

FIG. 6.

Cross-tolerance to other antibiotics. After 4 h of exposure to the antibiotics indicated at the x axis, the bacteria were reexposed to five different antibiotics, indicated at the top of each graphs. Two repetitions were performed, both of which are shown. The bars represent the ratios of the density of surviving cells (after the second exposure) relative to the initial density at reexposure. The control values are the ratios of the density of surviving naïve cells after 2 h of exposure (to the antibiotic at the top of the graph) relative to the initial density. The concentrations of the antibiotics at the first and second exposure were as follows: 0.0625 μg/ml for ciprofloxacin, and 24 μg/ml for ampicillin, rifampin, streptomycin, and tetracycline. The controls in this experiment are the same as those in Fig. 5. Abbreviations: CIP, ciprofloxacin; AMP, ampicillin; RIF, rifampin; STR, streptomycin; TET, tetracycline.

In general, we cannot conclude that phenotypic tolerance to one class of antibiotic renders the bacteria equally tolerant to other classes of antibiotics, although in most cases some level of cross-tolerance was observed. Exposure to all five antibiotics was followed by tolerance to themselves and cross-tolerance to three or four different drugs.

Potential clinical implications of phenotypic tolerance.

To explore the possible clinical implications of phenotypic tolerance, we developed a model of antibiotic treatment similar to that employed in references 25 and 30. For the pharmacokinetics of this model, we assume that the effective concentration of the antibiotic declines exponentially between doses and administered a fixed dose of antibiotic every 8 or 12 h. For the pharmacodynamics, we combine a Hill function (30) with the phenotypic tolerance model. We assume the relationship between the concentration of the antibiotic and the rate of growth (or death) of the sensitive subpopulation is defined by a Hill function, while the rate of growth (or death) of the tolerant subpopulation is not affected by the antibiotic concentration. As a consequence of antibiotic treatment, the tolerant subpopulation is enriched. However, since the concentration of the antibiotic is continually changing, the intensity of enrichment for the tolerant subpopulation also varies with time. A more detailed description of this phenotypic tolerance model is in the Appendix.

To illustrate the effects of tolerance, we monitor the changes in the density of bacteria over the course of 5 days with 8-h antibiotic dosing regimens in the absence of tolerance and with two values of the tolerance parameter f (Fig. 7a). In Fig. 7b, we consider the effects of a 12-h dosing regimen in the absence of tolerance and with two values of f. The results of this analysis clearly illustrate that the microbiological course of treatment can be profoundly affected by phenotypic tolerance. A treatment regimen that rapidly clears an infection in the absence of tolerance can fail to do so if there is phenotypic tolerance.

DISCUSSION

When growing populations of bacteria are exposed to bactericidal concentrations of antibiotics, the rate of mortality commonly decreases with time, and substantial fractions of the bacteria survive (8-10, 13, 16-18, 20, 30). Here, we explored the generality and details of this phenomenon and performed experiments to elucidate its cause. We present evidence that when exponentially growing populations of E. coli CAB1 (or K-12 MG1655) are exposed to bactericidal concentrations of antibiotics of five different classes (ampicillin, ciprofloxacin, rifampin, streptomycin, and tetracycline), the rate of mortality rapidly declines, and a substantial fraction of the bacteria are viable at 24 h. In some cases, the populations even grows again.

With the aid of mathematical models, we developed and explored the properties of three hypotheses to account for this phenomenon: (i) antibiotic decay, (ii) inherited resistance, and (iii) phenotypic tolerance. Although these hypotheses are not mutually exclusive, our experiments show that only the phenotypic tolerance hypothesis provides a sufficient explanation for the decreasing rate of mortality of bacteria exposed to all five antibiotics and for the survival of substantial fractions of their populations.

The antibiotic decay hypothesis cannot explain the decrease in the rate of mortality of E. coli CAB1 exposed to ampicillin, rifampin, and tetracycline, because the effective concentrations of these antibiotics did not decline with time. A small reduction in bactericidal activity was observed for ciprofloxacin and streptomycin during the period of exposure; therefore, we cannot rule out a contribution of antibiotic decay to the decrease in bacterial mortality for these two drugs. However, even after 5 h, these two antibiotics remain strongly bactericidal, and the decay in their effective concentration is not sufficient to account for the observed decrease in mortality or the survival of bacteria in medium with these antibiotics. While mutants resistant to streptomycin and rifampin arose in some of our time-kill experiments, these phenomena cannot be explained by inherited resistance. A similar rate of decrease in the rate of mortality and survival of the exposed bacteria was also observed in the absence of inherited resistance or partial resistance to streptomycin and rifampin as well as the other three antibiotics. Moreover, when we repeated these time-kill experiments with bacteria surviving exposure and regrown in antibiotic-free medium, the dynamics were the same as those observed with naïve cells. This would not be anticipated if there was evolved resistance in the previously exposed populations.

To explore the predictions of the phenotypic tolerance hypothesis, we constructed a mathematical model of this process in which we assumed that the bacterial population consists of a phenotypically sensitive subpopulation and a phenotypically tolerant subpopulation. We assume that during cell division there is a probability that a daughter cell will be tolerant and one minus that probability that it will be sensitive. This probability is the same for dividing tolerant and sensitive bacteria. In this model, the decrease in mortality of the total bacterial population is caused by an enrichment of phenotypically tolerant bacteria in the presence of antibiotics. The results of our experiments with all five antibiotics were fully consistent with the two predictions of this model. (i) Bacteria isolated after 30 min of exposure were more susceptible to killing by antibiotics upon reexposure than bacteria isolated after 1.5 to 3 h of exposure. (ii) As noted above, when the bacteria surviving exposure were cultured in the absence of antibiotics, their susceptibility was the same as that of a naïve population.

Our experiments also suggest that the tolerant state is robust and general and can extend to higher concentrations of the antibiotic than to the concentration to which they were exposed and to other antibiotics. Except for bacteria grown in higher concentrations of tetracycline, bacteria present later in time-kill experiments, during the tolerant phase, are substantially less susceptible to higher concentrations of the antibiotic to which they were exposed than naïve bacteria. Also, depending on the antibiotic the bacteria were exposed to, bacteria isolated during the tolerant phase are less susceptible to antibiotics of other classes than naïve bacteria are.

We believe that the phenotypic tolerance observed in these studies with exponentially growing bacteria is different from the antibiotic tolerance previously described for drugs that inhibit cell wall synthesis (32-36). This phenomenon appears to be due to the exposed bacteria being at stationary phase and for that reason refractory to antibiotics. On the other hand, the phenotypic tolerance observed here with E. coli CAB1 and these five different classes of antibiotics may be the same as what has been referred to as adaptive resistance in the studies of Pseudomonas aeruginosa exposed to aminoglycosides (2, 3, 10, 11, 20, 39). In those investigations, a lower sensitivity to the bactericidal effects of these antibiotics was observed for antibiotic-free cultures derived from the survivors of exposed cells relative to that for unexposed cells. The level of this sensitivity increased and eventually became similar to that of naïve cells with an increase in the amount of time these preexposed bacteria were maintained in antibiotic-free medium. It is also possible that the small-colony variants isolated among the survivors of Salmonella enterica serovar Typhimurium and Staphylococcus aureus exposed to aminoglycosides may be a manifestation of phenotypic tolerance as considered here (31, 37). When recultured in the absence of antibiotics, these small-colony variants give rise to normal colonies which are as sensitive to the antibiotics as naïve cells.

In this study, we focused on the population dynamics and the potential clinical implications of phenotypic tolerance and have not explored the cellular, physiological, or molecular processes responsible. The mathematical model of phenotypic tolerance we developed here is not mechanistic, as it does not specify the biological mechanisms responsible for either physiological variation in sensitivity to antibiotics within an isogenic population or for the transition between the susceptible and tolerant states. Moreover, this model is only a minimalist caricature of the phenotypic tolerance phenomenon in that it assumes that the bacterial population consists of only two distinct homogeneous subpopulations, susceptible and tolerant. In reality, there would almost certainly be a continuous distribution in the extent of susceptibility. It should be noted, however, that the same qualitative outcome would occur with a continuous distribution; exposure to antibiotics would enrich the less-susceptible cells and thereby reduce the overall susceptibility to the lethal effects of these antibiotics. This variation in susceptibility could be a reflection of the variation among the cells with respect to their stage in the replication cycle. It could also be a consequence of stochasticity (noise) in the cellular, physical, and biochemical processes affecting gene expression (14). Even for a single bacterium, temporal variation in cellular processes can occur in the absence of external stimuli (23). Also contributing to this variation in susceptibility or possibly reflecting it are the physiological (metabolic) and morphological changes observed in bacteria exposed to antibiotics (13, 24, 26, 38).

Two recent studies have investigated the phenomenon of phenotypic tolerance. Miller et al. (28) showed that induction of the SOS response by ampicillin can protect E. coli against the bactericidal effects of ampicillin by disturbing cell wall synthesis and growth. Balaban et al. (1) showed that there is variation in growth rate in a genetically homogeneous population and that the cells with lower growth rates (before exposure) survived exposure to ampicillin better than normally growing cells. While the killing kinetics of different classes of antibiotics vary due to due to the different mechanisms of action (30), exposure of bacteria to any one of these classes of antibiotics results in survival of a minority of the population. However, the mechanisms of tolerance (persistence) demonstrated for ampicillin (1, 28) might not account for phenotypic tolerance for all classes of antibiotics. Our observation of cross-tolerance in some combinations of antibiotic exposures and reexposures suggests that tolerance mechanisms could be shared by some classes of antibiotics but probably not by all. Massive changes in gene expression leading to changes in the syntheses of proteins of metabolic and stress response pathways and cell division during exposure of E. coli to ampicillin and ofloxacin have recently been observed (19). A number of these alterations in the gene expression levels were shared between bacteria exposed to ampicillin and ofloxacin. Keren et al. (21, 22) suggest that random fluctuations in gene expression are responsible for the formation of specialized persister cells. These cells overexpress toxins which, at high concentrations, can shut down the function of multiple drug targets (such as protein synthesis and DNA replication) and thereby prevent the antibiotic from corrupting the function of the target molecules. The HipA and RelE toxins have been shown to be directly involved in multidrug tolerance in E. coli (22).

Does phenotypic tolerance matter clinically? Although we did not investigate the consequences of phenotypic tolerance in a clinical setting, we assessed its potential microbiological consequences by using a mathematical model of antibiotic treatment. In this model, we combine the phenotypic tolerance model with the pharmacodynamics and pharmacokinetics of antibiotics. Our simulations of a periodic dosing antibiotic treatment regimen (Fig. 7) illustrates that phenotypic tolerance could have a substantial effect on the rate of clearance of a bacterial population and could actually prevent clearance in a situation where treatment would be effective in the absence of tolerance. We believe that these in vitro experimental results and this a priori consideration of the microbiological consequences of phenotypic tolerance in patients treated with antibiotics are sufficiently compelling to warrant the study of this process in more detail and explore its implications for the rational design of antibiotic treatment regimens.

Acknowledgments

We thank work study people for technical assistance.

This research was funded in part by grants from the U.S. National Institutes of Health (GM33782 and AI40662), The Wellcome Trust (IPRAVE project) (to B.R.L.), and the Spanish Pneumococcal Infection Study Network (G03/103) (to F.B.).

APPENDIX

Mathematical models for the three hypotheses. (i) Antibiotic decay.

In this model, we consider a bacterial population of density N (number of CFU per milliliter) that is homogeneous with respect to its susceptibility to the antibiotics. The rate of change in the density is given by the differential equation

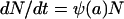graphic file with name M1.gif (1)

where ψ(a) is the pharmacodynamic function (30) which describes the relationship between the bacterial growth coefficient, ψ, (which can take on positive or negative values) and the antibiotic concentration, a:

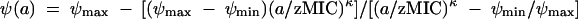graphic file with name M2.gif (2)

This pharmacodynamic function is derived from a simple Hill function, and is commonly referred to as the Emax model or Zhi model (29). The parameter ψmax is the maximum growth rate coefficient in the absence of antibiotics, ψmin is the minimum net growth rate coefficient at the highest possible antibiotic concentrations, zMIC is the pharmacodynamic MIC of the antibiotic [i.e., the antibiotic concentration that causes ψ(zMIC) = 0], and κ is the Hill coefficient, a measure of how fast the net bacterial growth rate coefficient, ψ, changes around the zMIC.

We assume that the antibiotic concentration, a, decays exponentially over time at a rate γ per hour. The rates of change in the concentration of the antibiotic are given by the differential equation

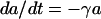graphic file with name M3.gif (3)

If _a_0 is the initial concentration of the antibiotic, the concentration at time t would be given by

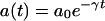graphic file with name M4.gif (4)

This model can be solved analytically, but in our simulations (Fig. 2a) we solved it numerically using the Berkeley Madonna program. This model predicts that, if _a_0 is >zMIC, N declines initially for a for the time interval of length 1/γ ln(_a_0/zMIC), and starts to increase after that. The rate of growth of N converges to ψmax (Fig. 2a).

(ii) Inherited resistance.

In this model, we divide the bacterial population into two subpopulations, one that is genetically sensitive and one that is genetically resistant to the antibiotic with densities of S and R CFU per milliliter, respectively. We assume that, in the absence of antibiotics, sensitive and resistant bacteria grow at rates rS and rR, respectively. In the presence of antibiotics, sensitive bacteria die at a rate mS, while there is no mortality of resistant bacteria.

The rates of change in the densities (CFU per milliliter) of sensitive and resistant cells in this population are given by the differential equations

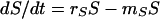graphic file with name M5.gif (5)
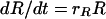graphic file with name M6.gif (6)

This model predicts that as long as the resistant cells are rare initially and mS is >0, the total population (S + R) will initially decline. As long as there are resistant cells in the population initially, they will necessarily increase in density and when the number of resistant cells exceeds the number of sensitive cells, the total population will increase again, and the growth rate of the total population converges to rR (Fig. 2b).

(iii) Phenotypic tolerance.

In this model, we assume that bacterial cells can exist in two physiological states, sensitive and resistant, with densities S and T CFU per milliliter, respectively. In contrast to the inherited resistance model, these states are not inherited; when a new bacterial cell arises, the probability, f, that it will be tolerant is independent of the state of the cell from when it came. We assume that these phenotypically sensitive and tolerant bacteria replicate at rates rS and rT, respectively, and are killed at rates mS and mT, respectively. The rates of change in the densities of these two phenotypes are given by

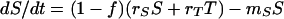graphic file with name M7.gif (7)
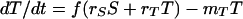graphic file with name M8.gif (8)

In the absence of antibiotics, mS = mT = 0 and as long as rS and/or rT is >0, the total population would be growing exponentially, and the relative frequency of phenotypically tolerant bacteria converges to f. We assume that in the presence of antibiotics, mS ≫ mT. The model predicts that, in this case, the relative frequency of phenotypically tolerant cells will increase, and the rate of mortality of the total population will decline.

Mathematical model to assess the clinical implications of phenotypic tolerance.

To illustrate the impact of phenotypic tolerance on treatment efficacy, we use a model that combines the phenotypic tolerance model with models of pharmacodynamics and pharmacokinetics of the antibiotic.

In this model, we assume bacteria of two physiological states, sensitive and tolerant, with densities S and T CFU per milliliter. For the pharmacokinetics, we assume that a dose of _a_0 is administered every 8 or 12 h and that the antibiotic concentration declines exponentially at a rate, γ.

In the above phenotypic tolerance model (equations 7 and 8), the replication rate of sensitive and tolerant subpopulations are not independent. Hence, to combine the pharmacodynamics with the pharmacokinetics, we need to separate the pharmacodynamic function of these two populations into replication and mortality rates. To describe the pharmacodynamic relation between the mortality rate constant, μ_S_, of the phenotypically sensitive bacteria and the antibiotic concentration, a, we use a Hill function:

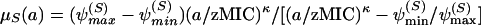graphic file with name M9.gif (9)

where the parameters are defined as in the antibiotic decay model shown above. The mortality rate constant, μ_S_, relates to growth rate coefficients (in equation 2) in the following way: μ_S_ = ψmax − ψ(a). As in the above phenotypic tolerance model, we assume that the tolerant bacteria are not killed by the antibiotic. With these definitions and assumptions, the rates of change in the concentration of the antibiotic between doses and densities of the sensitive and tolerant populations are given by

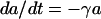graphic file with name M10.gif (10)
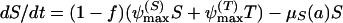graphic file with name M11.gif (11)
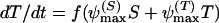graphic file with name M12.gif (12)

The superscripts S and T refer to the sensitive and tolerant states, respectively. To generate Fig. 7, we used the Berkeley Madonna program to solve these three differential equations, with the program adding _a_0 micrograms of the antibiotic per milliliter every 8 or 12 h. The predictions of this model presented in this paper are unaffected by the fact that N can take on integer or noninteger values. Under certain conditions (combinations of parameters) where cell densities approach zero and possibly take on noninteger values, the model is not valid. Also, this model does not take into account possible effects of the host's immune response on the bacterial survival and killing. However, this model was not intended to determine exact concentrations that would lead to complete clearance but rather to demonstrate the phenomenon.

REFERENCES