Distribution and intensity of constraint in mammalian genomic sequence (original) (raw)
Abstract
Comparisons of orthologous genomic DNA sequences can be used to characterize regions that have been subject to purifying selection and are enriched for functional elements. We here present the results of such an analysis on an alignment of sequences from 29 mammalian species. The alignment captures ∼3.9 neutral substitutions per site and spans ∼1.9 Mbp of the human genome. We identify constrained elements from 3 bp to over 1 kbp in length, covering ∼5.5% of the human locus. Our estimate for the total amount of nonexonic constraint experienced by this locus is roughly twice that for exonic constraint. Constrained elements tend to cluster, and we identify large constrained regions that correspond well with known functional elements. While constraint density inversely correlates with mobile element density, we also show the presence of unambiguously constrained elements overlapping mammalian ancestral repeats. In addition, we describe a number of elements in this region that have undergone intense purifying selection throughout mammalian evolution, and we show that these important elements are more numerous than previously thought. These results were obtained with Genomic Evolutionary Rate Profiling (GERP), a statistically rigorous and biologically transparent framework for constrained element identification. GERP identifies regions at high resolution that exhibit nucleotide substitution deficits, and measures these deficits as “rejected substitutions.” Rejected substitutions reflect the intensity of past purifying selection and are used to rank and characterize constrained elements. We anticipate that GERP and the types of analyses it facilitates will provide further insights and improved annotation for the human genome as mammalian genome sequence data become richer.
Recent comparisons among the human, mouse, and rat genomes have suggested that ∼5%–6% of the bases in a mammalian genome exhibit evidence of past purifying selection (Mouse Genome Sequencing Consortium 2002; Cooper et al. 2004a; Rat Genome Sequencing Project Consortium 2004). This small fraction of the genome includes most known protein-coding exons and the majority of known transcriptional regulatory elements (Rat Genome Sequencing Project Consortium 2004). Considering such estimates, as well as recent studies that successfully leveraged sequence conservation to identify regions of functional importance in mammals (Pennacchio et al. 2001; Göttgens et al. 2002; Boffelli et al. 2003; Ghanem et al. 2003; Brugger et al. 2004), it is clear that comparative sequence analysis is a powerful paradigm for the discovery of those functional regions in the human genome whose experimental discovery is difficult (O'Brien et al. 1999; Hardison 2000; Pennacchio and Rubin 2001; Cooper and Sidow 2003). Equally important as discovery, however, is the quantification of constraint among conserved regions. Stratification of elements according to the intensity of past constraint is an important metric, which, in the form of evolutionary rates, has been in use in analyses of protein evolution since the beginnings of molecular evolutionary studies (Li 1997).
Nonexonic elements constitute a majority of the constrained 5%–6% of the human genome (Dermitzakis et al. 2002, 2003; Mouse Genome Sequencing Consortium 2002; Cooper et al. 2004a; Rat Genome Sequencing Project Consortium 2004), but the total amount of constraint that has acted upon these classes of elements throughout mammalian evolution is unknown. Similarly, a biologically transparent and generally applicable stratification of their predicted importance has been elusive. Consider a class of elements previously identified as “ultraconserved” on the basis of human, mouse, and rat alignments; having only three sequences to compare necessitated defining these elements on the basis of length and perfect identity (Bejerano et al. 2004). With richer sequence alignments, such criteria become obsolete, and the observed intensity of past constraint becomes a general scale on which to rank all elements. Ultraconserved elements can then be appropriately defined as those that exhibit the strongest past constraint. Another popular means of extracting very important elements is alignment to distant genomes, such as fish or chicken. This confounds the age of the element with its importance for the organism, as there are mammalian-specific elements that are under equally strong constraint as those detected by alignment with other vertebrates. A universal metric for constraint that is independent of the phylogenetic scope of the comparison would clearly be desirable, such that importance of the element is estimated independently from its age.
A novel approach that estimates constraint directly is necessary, because currently available strategies for the identification and characterization of constrained elements (Gumucio et al. 1992; Dubchak et al. 2000; Mayor et al. 2000; Sumiyama et al. 2001; Boffelli et al. 2003; Margulies et al. 2003; Cooper et al. 2004a; Shah et al. 2004; Siepel and Haussler 2004a) suffer from one, or multiple, of several general drawbacks. First, some methods use simple scoring metrics such as percent identity or consensus sum-of-pairs in the interest of computational efficiency, but at the expense of interpretability or statistical robustness. Second, to gain sufficient power for identifying constrained elements, most methods use windowing heuristics that enforce an effectively arbitrary limit to the resolution of the analysis. Third, some methods produce _P_-values, which are then used in a rule-based framework for the discrimination of “conserved” vs. “nonconserved,” a discrete classification that ignores variation in the intensity of constraint; this discrete classification is used because no quantitative relationship between _P_-values and intensity of constraint has been explored. Fourth, some methods require assumptions about the expected appearance or abundance of neutral DNA. Finally, most methods do not deal properly with gaps, making them prone to serious artifacts.
The future influx of large amounts of genomic sequence data provides the opportunity to devise methods that more effectively leverage the greater power that comes with more sequences, and which more realistically model the evolutionary process underlying constraint. A brief consideration of the population genetics underlying comparative analyses underscores this point. Due to their deleterious nature, mutations that arise within functional elements are more likely to be subject to purifying selection. They are therefore less likely to be fixed in the population and result in evolutionary change (Kimura 1983). The more deleterious a mutation is, the greater the tendency for purifying selection to eliminate it. Thus, the direct consequence of purifying selection is a deficit of substitution events within functional elements as compared with neutral DNA, with the magnitude of the deficit relating to the strength of the constraints that have acted upon it.
It is with these considerations in mind that we developed “Genomic Evolutionary Rate Profiling” (GERP; Fig. 1A). Using GERP, we analyzed a multiple sequence alignment containing ∼1.9 Mbp of the human genome aligned with sequences from 28 diverse mammals capturing ∼3.85 neutral substitutions per site (subs/site). We identify constrained elements that collectively span ∼5.5% of the locus. The score distribution and regional clustering of these elements, and their overlap with features such as repeats and exons, reveal a variety of insights about the actions of purifying selection on this locus. These insights foreshadow general conclusions relevant to the future characterization of constrained elements throughout the human genome.
Figure 1.
Overview of GERP. (A) Each column of the compressed alignment (corresponding to each base of the human sequence) is analyzed independently. Number of substitution events is inferred, giving “observed” values (see Methods); the “expected” rate for each column is determined by summing the branches of the neutral tree that remain after removing species with a gap character (compare the black, red, and blue neutral trees with the correspondingly colored expected rates). Candidate constrained regions are identified as consecutive columns of observed rates smaller than the expected rates (black boxes). Nearby candidates are merged (gray box) across a limited number of unconstrained columns. Finally, each candidate is scored as the sum of the deviations from expectation at each column, collectively termed as “rejected substitutions.” (B) Neutral tree for the complete set of species analyzed here (see Methods); the tree is rooted arbitrarily for display purposes only, and analyses are performed using an unrooted tree. Primates are in green, non-primate placental mammals are in red, and marsupials are in blue.
Results
Overview of GERP
GERP is a framework for the identification of constrained elements that exploits the fact that purifying constraint results in a deficit of substitution events (see Methods for a thorough description). GERP estimates evolutionary rates for individual alignment columns, and compares these inferred rates with a tree describing the neutral substitution rates relating the species under consideration. It subsequently identifies candidate constrained elements by annotating those regions that exhibit fewer than expected substitutions. Each of these elements is scored according to the magnitude of the substitution deficit, measured as “rejected substitutions” (RS) (Fig. 1A).
There are several aspects of GERP that collectively distinguish it from previous methods. First, alignment columns are analyzed individually rather than in sliding windows (Fig. 1A). Second, GERP includes a null model (see below) that requires no annotation and no assumptions about the abundance of neutral DNA. Third, we eliminate all gaps from each column for the determination of both “observed” and “expected” rates of evolution (Fig. 1A).
The elimination of gap characters is an important feature facilitated by the single-column approach. On some occasions, it may sacrifice some biological information. However, stochastic models that appropriately parameterize the spectrum of evolutionary changes that lead to gaps within alignments are not available, and will likely remain elusive for the foreseeable future. In addition, missing data and assembly mistakes produce alignment gaps that should be ignored. Such data limitations will be unavoidable in mammalian genomic sequence data, particularly in the “draft” genomes of most nonhuman mammals, but also in “comparative grade” sequence (Blakesley et al. 2004). Finally, lineage-specific loss of a given element should not impair its detection within those species in which it has remained functional. This is particularly important in light of the goal of comprehensively identifying functional elements in the finished human sequence (Collins et al. 2003; The ENCODE Project Consortium 2004).
Confidence, sensitivity, and robustness
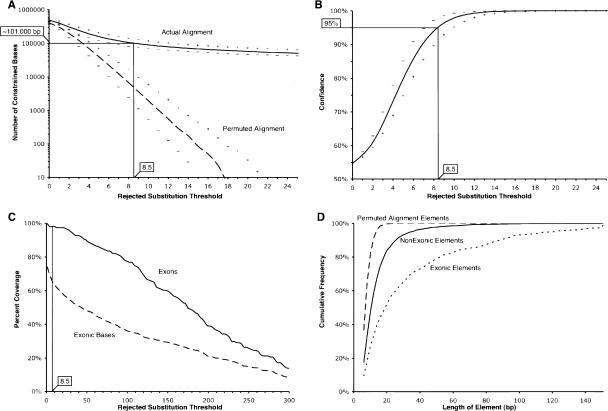
During the evolution that generated the extant sequences, some sites or regions experienced fewer substitutions than others, even in the absence of selective effects. This is because substitution events occur stochastically, and some actually neutral alignment columns that happened to experience fewer substitutions may by chance be grouped, and together appear as a constrained element. It is therefore important to construct a null model for defining significance thresholds against a neutral background. We model the false-discovery process by randomly permuting the alignment columns to generate a new alignment, whose constrained elements are viewed as false-positive predictions. The total number of constrained bases identified in a permuted alignment, as a fraction of the number of constrained bases in the original alignment, defines a reliability metric we call confidence (Fig. 2; see Methods). The number of false-positives decreases rapidly as the RS score threshold is raised from 0 to 25 rejected substitutions (Fig. 2A), with the sum of the lengths of neutrally evolving regions identified as “constrained,” dropping from 400,000 bases with a threshold of 0 RS, to 0 bases using a threshold of 25 (Fig. 2B). GERP achieves ∼95% confidence with a threshold of 8.5 RS for this alignment using a neutral rate estimate of 3.85 subs/site.
Figure 2.
Confidence and sensitivity of GERP as a function of the rejected substitution threshold used to identify constrained elements. (A) Number of constrained element bases identified in the real alignment (solid line) and permuted alignments (dashed line). (B) Confidence is defined as the number of constrained element bases in the actual alignment divided by the sum of the constrained element bases in the actual and permuted alignments (see Methods). In A and B, the curves indicated with “+” and “–” characters result from analyses using a neutral rate estimate that is 10% greater or less, respectively, than the estimate of 3.85 neutral subs/site. A vertical black line marks the RS score threshold of 8.5 (corresponding to a confidence of ∼95%). (C) The fraction of exons that overlap at least one constrained element (solid line), and the fraction of exonic bases within a constrained element (dashed line). (D) Cumulative frequencies of the sizes of constrained elements at an RS of 8.5 or greater, with permuted alignment elements (heavy dashed line), exclusively nonexonic constrained elements (solid line), and exonic elements (light dashed line).
While a proper estimate of sensitivity is difficult in the absence of a representative sample of “true positives,” we can determine sensitivity to exons and exonic bases. GERP is highly effective at identifying constrained sequence within exons; using the RS threshold of 8.5, at least one constrained element is identified overlapping all but three of 151 exons in the region (see Methods), and ∼64% of the ∼37,000 exonic bases are covered (Fig. 2C). The vast majority (∼83%) of the missing exonic bases reside within UTRs, which are generally under weaker constraints. Increasing the constrained element score threshold beyond 8.5 decreases sensitivity, with ∼4000 exonic bases lost as the threshold is increased to 25. However, the majority of exons overlap at least one constrained element, even at thresholds in excess of 100 (Fig. 2C). Overall, the exon-coverage statistics demonstrate that GERP is effective at capturing known functional sequence, even at stringent thresholds.
Concomitant with estimating error rates in the discovery process, we also evaluated the effect that errors in the neutral rate estimate might have. Neutral rate estimates can be difficult to make with high precision, and often vary slightly depending on the method used or on the program that generated the alignments (Rat Genome Sequencing Project Consortium 2004). We therefore quantified the effect of a 10% variation in the neutral rate estimate on constrained element discovery (Fig. 2A,B). Because the RS threshold used to define significance is estimated by the permutation analyses, GERP maintains high confidence with the modified neutral rate estimate. For example, using a neutral rate estimate of 4.24 subs/site (10% higher than our estimate of 3.85), GERP calculates an RS score threshold of 10.0, which provides a similar number of total constrained bases and a similar confidence to that observed using a threshold of 8.5 and a neutral rate of 3.85 subs/site (Fig. 2A,B; compare the solid line at an RS of 8.5 to the “+” line at an RS of 10). The null model thus makes GERP robust to errors in the neutral rate estimates. We consider this capacity for error correction to be an important feature of our approach.
Distribution of constrained elements
The size distributions of elements identified with a score of 8.5 or better differ significantly between exonic and nonexonic groups, and also between those elements identified in the actual and permuted alignments (Fig. 2D). As expected, constrained elements identified in the permuted alignments tend to be smaller than those in the real alignment. The largest element discovered in 10 independent permutations is 30 bp with an RS score of 9.6, while the highest scoring element in these same 10 permutations is a 14-bp element with a score of 20.7. Constrained elements discovered in the actual alignment range in size from 3 bp to >300 bp. We find over 2000 elements below 10 bp in size, indicating a resolution that is well within the range of typical transcription-factor binding sites. While a fraction of these small elements are probably false positives, we observe elements as small as 7 bp at an RS threshold of 21, a threshold that excludes all of the constrained elements identified in the permuted alignments. If we enrich for small, high-scoring elements, we identify 4-mers that score over 15 (>99.8% confidence) and 6-mers that score over 21, further confirming the rigorous detection of small constrained elements.
Exonic regions show a clear enrichment for larger, higher scoring elements, with over half of the exonic elements being larger than 18 bp, compared with only 20% of the nonexonic elements (Fig. 2D). This size differential is consistent with the likely influence of false-positive elements within the nonexonic group, but is also probably related to biological differences between these two classes. Consistent with many previous studies (Dermitzakis et al. 2002, 2003; Mouse Genome Sequencing Consortium 2002; Margulies et al. 2003; Cooper et al. 2004a; Rat Genome Sequencing Project Consortium 2004), the majority of constrained elements that we identify do not overlap exons, even at high stringency. Nonexonic elements outnumber exonic elements approximately seven to one, with the number of nonexonic constrained bases exceeding exonic bases approximately three to one. However, the ratio between exonic and nonexonic constrained bases does get closer to one as only the larger, higher scoring elements are considered. To obtain the total constraint under which nonexonic and exonic elements of this locus have evolved, we summed the total number of rejected substitutions estimated for these regions. This cumulative estimate is ∼100,000 rejected substitutions for nonexonic constraint vs. ∼50,000 for exonic constraint, suggesting that purifying selection eliminated twice as many nonexonic as exonic polymorphisms during the mammalian evolution of the locus.
Clustering and density of constrained elements
The density of constrained elements fluctuates significantly across the length of the locus (Fig. 3A). This fluctuation is weakly correlated with the density of exonic sequence (data not shown) and is inversely correlated to the density of repetitive elements; a simple linear regression model estimates that 32% of the variance in constrained element density is explained by repeat density (Fig. 3B). We also find that there is a sharp elevation in the density of constraint in regions flanking constrained elements. In fact, >25% of bases that lie between 3 and 100 bases from a constrained element are themselves within a constrained element, compared with a locus-wide average of only 5.5% (Fig. 3C). Furthermore, this increase in constraint density persists, but gradually declines, over the span of hundreds of bases away from the border of a given constrained element. Coding exons show a similar elevation in constrained bases nearby, with >95% of splice sites residing in constrained elements. The opposite trend is observed for repetitive elements, whose neighboring bases exhibit a deficiency of constrained elements relative to the locus-wide average.
Figure 3.
Constrained elements tend to cluster, and this clustering is inversely correlated with repetitive element density. (A) Densities of constrained elements (red) and repetitive elements (blue) along the length of the human CFTR locus. Densities are determined for consecutive, nonoverlapping 25-kb windows, and each window is normalized by the locus-wide average. The solid red line corresponds to constrained elements identified with a merging tolerance of one unconstrained column, as opposed to six unconstrained columns for the dashed line (Fig. 1A; see Methods). (B) Regional constrained element density vs. repetitive element density. The values for each 25-kb window used in A are shown. The equation and trendline correspond to a simple linear regression model relating the two variables, with an R2 value of 0.32. (C) Constrained element density as a function of distance from various features (see Methods); (solid red line) constrained elements with a merging tolerance of one unconstrained column; (dashed red line) constrained elements with a merging tolerance of six unconstrained columns; (green line) exons; (blue line) repeats. Note that the behavior of the red lines very near the origin is a result of the fact that a pair of elements cannot be within the “merge distance” of each other (see Methods).
Large constrained regions
We exploited the underlying regional clustering of constrained elements by modifying our detection methodology to find longer elements with higher cumulative constraint scores. Regions containing a high density of constrained elements are merged into single elements, while regions containing sparse or weakly constrained elements are lost due to the increased impact of unconstrained columns. (Unconstrained columns within a candidate element are penalized; see Methods and Supplemental Table 1.) The number of false-positive elements using this modified merging criterion and a rejected substitution threshold of 8.5 is trivial (Supplemental Fig. 1). Thus, while there is a significant cost in sensitivity to small, isolated, or weakly constrained elements, there are significant increases in confidence at a perelement level.
With this modified procedure, we retain a similar number of total bases comprising constrained elements, while decreasing the number of individual elements by over 10-fold, from 5961 to 581. The size distribution of constrained elements is now dramatically shifted toward long elements, with nearly half being >150 bp. This shift is seen for both nonexonic and exonic elements (Fig. 4A). Because we are eliminating small and isolated elements and merging the larger, denser elements, the density of constrained elements across the locus fluctuates more dramatically (Fig. 3A; dashed line), and the elevation in the density of constrained bases near constrained elements declines considerably (Fig. 3C; dashed line).
Figure 4.
Description of large constrained regions in the CFTR locus. (A) Sizes of constrained elements identified with a merging tolerance of six unconstrained columns, with the length in base pairs of each bin along the _x_-axis and the count for each bin along the _y_-axis. Bins are divided according to those elements that overlap exons (black) and those that do not (gray). (B) Large, non-coding constrained elements that overlap coding exons (see Methods). Each coding exon in the region is displayed in ascending order along the _x_-axis according to human genome coordinates. Exons are boxed according to which gene they belong, and transcription orientation of each gene is shown with an arrow. Note that in this format, the _left_-most exon is the first coding exon for all of those genes transcribed to the right, while the opposite is true for genes transcribed toward the left. The distance that the associated noncoding constrained elements extend away from the individual exons is plotted along the _y_-axis. Positive values are indicated for the 3′ direction, and negative values for the 5′ direction.
The clustering of constrained elements may be a consequence of degenerate bases interspersed among constrained bases within the actual functional element. Certain properties of known functional elements plausibly support this hypothesis, including third-position wobble in exons, transcription-factor binding sites containing degenerate bases, and clustering of transcription-factor binding sites that together regulate gene expression (Arnone and Davidson 1997; Berman et al. 2002; Markstein et al. 2002; Brugger et al. 2004). Thus, a major benefit of this adjustment may be that GERP is more effective at identifying regions that correspond more closely to functional units. Evidence for this hypothesis can be found in the coverage of exons by the enlarged elements. Despite failing to include five UTR exons and six small coding exons, coverage of exonic bases is increased by 12.5% (∼3000 bases) using the modified criteria, and the coverage of protein-coding sequence improves from 90.1% to 96.6%. Under the original criteria, there is a median value of three constrained elements per exon, while 115 of 128 coding exons are captured in their entirety by a single constrained element using the modified criteria.
Exon-associated noncoding constraint
We also sought to characterize the distribution of constraint in noncoding elements that span an entire coding exon (identified without the influence of the coding positions themselves; see Methods). The level of similarity between human and mouse sequence near exons has previously been analyzed and found to fluctuate, being generally higher near alternatively spliced than constitutively spliced exons (Sorek and Ast 2003). We find that the extent to which constrained elements extend away from the ends of exons varies substantially among the coding exons in this locus (Fig. 4B). Some terminate within a handful of bases from the beginning (or end) of the exon, while others extend for hundreds of bases in either direction. The ST7 gene, for example, has multiple isoforms annotated as RefSeq entries and appears to harbor a large amount of nonexonic constraint immediately flanking its coding exons (Fig. 4B). The dramatic gene-to-gene variation in exon-associated constraint possibly reflects gene-specific differences in the importance of regulated splicing.
Ancestral repeats contain constrained elements
Those mobile elements that inserted prior to the common ancestor of most mammals are often referred to as “ancestral repeats” (ARs). They have well-defined consensus sequences, are considered to be predominantly nonfunctional, and are therefore generally free to evolve in the absence of selective effects. Those that can still be aligned even among distant mammals have been used as models for neutrally evolving DNA (Mouse Genome Sequencing Consortium 2002; Ellegren et al. 2003; Hardison et al. 2003; Rat Genome Sequencing Project Consortium 2004; Yang et al. 2004). However, portions of such elements may have been recruited for important biological functions throughout evolution. Evidence that interspersed repeats in mammalian genomes may acquire functional roles as both protein-coding (Nekrutenko and Li 2001) and transcriptional regulatory regions (Chang-Yeh et al. 1991; Britten 1997; Jordan et al. 2003; Khambata-Ford et al. 2003; Peaston et al. 2004) has existed for quite some time. In addition, there is comparative evidence suggesting that at least some repetitive element fragments are conserved between human and mouse (Silva et al. 2003). In light of these observations, we compared our constrained element annotations with AR annotations to determine whether repetitive fragments show evidence of constraint even when compared across many diverse mammalian species.
As expected, the number of constrained element bases that reside within mammalian ARs drops dramatically as the RS threshold is increased from nonspecific to highly specific (data not shown). This similarity in behavior between ARs and the (false-positive) “constrained” elements identified in the permuted alignments supports the hypothesis that mobile elements accumulate evolutionary divergence in a predominantly neutral fashion. However, constrained elements overlapping ARs show a distribution that is clearly distinct from the permutation-based null model. There are 39 elements, spanning 1125 bp, that overlap an AR with an RS score greater than 21, which we discussed previously as a threshold exceeded by none of the elements in 10 independently permuted alignments. Additionally, there are three constrained elements overlapping an AR that score over 100 RS, a threshold that excludes over 20% of the exons in this locus. Collectively, constrained elements overlapping AR fragments exhibit evidence of nearly 6000 RS in this region, or ∼5% of the total amount of nonexonic constraint.
We also analyzed the overlap between the larger, higher scoring constrained elements (which are highly unlikely to be false positives) and ARs. We find over 2800 bases of overlap between these two classes of elements, covering nearly 50 different AR regions (Fig. 5A). There are 17 distinct AR remnants (>1% of all AR remnants) that contain more than 50 constrained bases, confirming that this finding is not based upon an isolated observation (Table 1). One example of an unambiguously constrained element overlapping an AR can be seen in Figure 5B; this section of the alignment corresponds to a portion of a constrained element contained within an L3 repeat, in which only a handful of substitution events are distributed across the more than 40 alignment columns seen. As a whole, this element exhibits an RS score of over 100, and is shared among most of the analyzed placental mammals (the gapped species are missing data for this portion of the sequence).
Figure 5.
Ultraconserved and mobile-element derived constrained elements. (A) The locations of three types of features are shown along the genomic coordinates of the human locus as follows: green squares indicate the locations of ancestral repeats that overlap constrained elements; orange triangles correspond to exons; and circles correspond to the ultraconserved elements (Table 2), broken down according to those that overlap exons (red), and those that do not (blue). RefSeq genes and their transcriptional orientation are marked by boxes and arrows, respectively. (B) A small alignment region corresponding to an ancestral repeat region (part of an L3 element) overlapping a constrained element scoring >100 rejected substitutions. Nucleotides are color-coded, and gaps are indicated in gray (the fully gapped placental species are missing data). The displayed region corresponds to positions 495,140–495,181 of the human sequence (with the first base of the locus being position 1).
Table 1.
Descriptions of ancestral mobile elements overlapping constrained elements
| Class | Starta | Stop | # Cons bases |
|---|---|---|---|
| L3 | 962280 | 962715 | 413 |
| L2 | 1052484 | 1053441 | 243 |
| MER121 | 508170 | 508518 | 181 |
| MIRb | 965209 | 965397 | 169 |
| L3b | 519500 | 519683 | 145 |
| L3 | 495138 | 495258 | 121 |
| L3b | 961929 | 962042 | 114 |
| L3 | 962047 | 962151 | 105 |
| L2 | 494399 | 494693 | 104 |
| MIRb | 1004227 | 1004449 | 101 |
| L2 | 994487 | 994603 | 97 |
| MIR3 | 462819 | 462999 | 83 |
| MIR3 | 994407 | 994484 | 78 |
| MIRb | 1726111 | 1726311 | 78 |
| L3b | 597760 | 597877 | 64 |
| Charlie8 | 1691311 | 1691570 | 60 |
| MIR | 959086 | 959154 | 56 |
Ultraconserved elements
A previous study identified ∼500 “ultraconserved” elements in the human genome (Bejerano et al. 2004). These elements were defined as regions from alignments of the human, mouse, and rat genomes that exhibited no changes over at least 200 bases. Many of these are tightly conserved with other vertebrates such as chicken and fish. These regions are prime targets for further characterization, as they contain functional elements playing critical roles in human biology. We propose to use rejected substitutions as a metric for defining ultraconserved elements in the context of multiple-sequence alignments of many diverse mammals. RS scores are guided by the intensity of constraint, require no artificial length criterion, and are appropriate for identifying and prioritizing elements that have undergone intense purifying selection throughout mammalian evolution. In fact, the modification to our method that enriches for large, high-scoring elements represents an ideal means to capture these important elements.
The human, mouse, and rat genomes are separated by a neutral rate of ∼0.65 subs/site (Cooper et al. 2004a). The criterion of 200 bases containing no substitution events among these three therefore amounts to 200 sites * 0.65 subs/site = 130 RS. We find 185 elements in the CFTR locus that exceed this score, including 80 (43%) that are exclusively nonexonic; most exons overlap with at least one such element. Extrapolated to the entire genome, as a rough guide only, these results imply that ∼280,000 tightly constrained elements exist throughout the human genome. These would cover a majority of coding exons (and a considerable amount of flanking DNA, in many cases), but would also include over 100,000 exclusively nonexonic elements.
However, this criterion is too weak to be of real value in the identification of the type of elements previously described, of which there are only ∼500 across the entire genome. Thus, one might consider scaling the constraint criterion as a function of the power of the analysis, in this case, the neutral rate. The score of 130 RS discovered with 0.65 neutral subs/site, for example, would scale to 770 RS with a neutral rate of 3.85 subs/site. We find 20 elements that meet this scaled constraint criterion, 16 of which have strong matches in the chicken genome (Table 2; Fig. 5B), and eight of which have strong matches in the Fugu genome (data not shown).
Table 2.
The locations and scores of ultraconserved elements in the CFTR locus
| Starta | Length | RS score | Type | Gene | Chick hitc |
|---|---|---|---|---|---|
| 747185 | 1442 | 2037 | CDS/3′UTR | CAPZA2 | 792, 72% |
| 1019532b | 978 | 1606 | Intron/CDS | ST7 | 972, 73% |
| 988235 | 957 | 1450 | Intronic | ST7 | NA |
| 1620561 | 895 | 1446 | CDS | CORTBP2 | 904, 79% |
| 528543 | 1284 | 1286 | CDS | CMET | 1289, 69% |
| 1047144 | 553 | 1158 | Intronic | ST7 | NA |
| 966907 | 992 | 1120 | Intronic | ST7 | 492, 60% |
| 183738 | 693 | 1114 | Intergenic | TES–CAV2 | 428, 75% |
| 1145460 | 935 | 1067 | Intronic | WNT2 | NA |
| 1150910 | 593 | 813 | Intronic | WNT2 | 250, 70% |
| 1421330 | 888 | 807 | Intronic/CDS | CFTR | 748, 68% |
| 388452b | 392 | 774 | CDS | CAV1 | 368, 80% |
| 611415 | 821 | 754 | Intronic/CDS | CMET | 358, 65% |
| 1002497 | 554 | 719 | Intronic | ST7 | 428, 71% |
| 1540687 | 637 | 717 | CDS/3′UTR | CORT2 | 628, 68% |
| 534395 | 723 | 702 | Intronic | CMET | 559, 67% |
| 963235 | 955 | 692 | Intronic/CDS | ST7 | 668, 57% |
| 604385 | 476 | 649 | Intronic/CDS | CMET | 314, 71% |
| 1613714b | 362 | 644 | Intronic/CDS | CORT2 | 349, 79% |
| 527928 | 608 | 575 | Intronic | CMET | NA |
The longest and highest-scoring element overlaps the terminal coding exon and much of the 3′ UTR of the CAPZA2 gene (see the last exon of CAPZA2 in Fig. 4B). CAPZA2 codes for an actin-binding protein, and the 3′ UTR of this gene has previously been shown to be highly conserved among the human, mouse, and chicken orthologs (Hart et al. 1997). The second highest-scoring element includes a coding exon of the ST7 gene, but is predominantly intronic. The intronic portion of this element has been described as a constrained element likely to have functional properties related to RNA secondary structure (Margulies et al. 2003). We find that this element is highly conserved among all of the mammals analyzed here (except for wallaby, bat, pig, and marmoset, which are gapped due to missing data). Contrasted to a neutral rate of over three subs/site among the included species, this element contains a 194-nucleotide region exhibiting a handful of small changes, with one substitution occurring in the rodent lineage, one insertion in the galago, and all other changes occurring in the marsupial lineage. There is a stretch of over 200 bases with no changes among 19 of the placental mammals analyzed here. Additionally, this element has a match (not including the coding exon) in the chicken genome that is 93% identical to the human sequence.
While extrapolation from a single locus is clearly error-prone, the 20 ultraconserved elements that we identify would suggest that ∼30,000 such elements, spanning over 2,000,000 (∼0.07%) bases, exist in the human genome. If it holds true, this number is many times larger than the previous genome-wide estimate. At the very least, there are likely to be more elements than previously suggested, as none of the 20 that we identify in the CFTR locus were found in the previous study (Bejerano et al. 2004).
Discussion
Biological insights
The current implementation of the GERP methodology and application to our comparative data set has yielded a variety of biological insights. Using reasonable confidence thresholds, we identify constrained elements spanning over 100,000 bp, most of which are not exonic. Constrained elements tend to cluster closely to each other, separated by small numbers of unconstrained or very weakly constrained bases. This observation can be exploited by our methodology to identify large constrained regions that are likely to correspond more precisely to functional elements. We note that these larger constrained elements have high confidence, and yet they capture most exons as single units and nearly 97% of RefSeq protein-coding bases. There are nearly 600 of these regions in the CFTR locus, over 400 of which are exclusively nonexonic. Collectively, these regions represent a rich set of targets for experimental and population genetic characterization.
We show that the total constraint that has acted upon nonexonic regions in the CFTR locus exceeds that of exonic regions by a ratio of two to one. The observation that many nonexonic elements under intense purifying selection exist in the human genome has been made previously by multiple, independent studies (Dermitzakis et al. 2003; Margulies et al. 2003; Bejerano et al. 2004; Cooper et al. 2004a). Our results, in which we measure total constraint directly, provide further quantitative challenge to the hypothesis that the search for functional variants in human populations would be more effective if confined primarily to coding exons and promoter sequences (Botstein and Risch 2003). We suggest that such efforts should eventually be guided by constrained element annotations, and that the accumulation of more mammalian genome sequence data will make this an achievable goal (Collins et al. 2003).
We detect unambiguously constrained elements within mammalian ancestral repeats. Consistent with these results, a previous analysis of this region found that ∼2% of constrained bases overlap with ARs (Margulies et al. 2003), but this was interpreted as the false-discovery rate rather than the effect of legitimate constraint; our analysis suggests that many of these are likely to be real. While as a whole they remain a good model for neutrally evolving DNA in mammalian genomes, interpretations of ancestral repeat alignments as strictly neutral should be considered with this fact in mind. In conjunction with evidence from previous studies of the functional “domestication” of mobile element fragments (Chang-Yeh et al. 1991; Britten 1997; Jordan et al. 2003; Khambata-Ford et al. 2003; Silva et al. 2003; Peaston et al. 2004), we conclude that portions of mobile elements are occasionally co-opted into crucial biological roles that are shared among many diverse mammals. These elements show evidence of intense levels of purifying selection, in some cases comparable to or greater than that experienced by protein-coding exons.
Using RS scores to rank constrained elements, we describe a small group of elements in this locus that have been under an intense level of purifying selection. Elements similar to these were previously identified throughout the human genome on the basis of their length in human, mouse, and rat alignments (Bejerano et al. 2004). While that criterion works well using three-species alignments, our method provides a better framework for their identification in deeper mammalian alignments. Indeed, we show that there are many more such elements than previously estimated, and that the GERP approach can improve their detection with richer comparative data sets.
Furthermore, while genomic comparisons with more distant vertebrates such as chicken (Hillier et al. 2004) and Fugu (Aparicio et al. 2002) may also uncover critically important functional elements in the human genome (Nobrega et al. 2003; Woolfe et al. 2004), these approaches will miss many elements, including all of those that specify unique mammalian traits. Indeed, we find that over half of the ultraconserved elements in the CFTR locus have no match to fishes, and 20% (including four of the nine exclusively nonexonic ultraconserved elements) have no match with chicken, despite the fact that these elements are all under similarly intense levels of purifying selection within mammals (Table 2). We conclude that there is a substantial fraction of mammalian-specific noncoding constrained elements whose importance is equal to or exceeds that of pan-vertebrate elements.
Conclusions
Mammalian genomic sequence data is accumulating rapidly and will become extremely rich in the future. Typical comparative data sets will have many diverse placental mammals capturing multiple neutral subs/site. The ENCODE project, for example, will generate sequence data from eight or more diverse mammals covering regions that are orthologous to ∼1% of the human genome (The ENCODE Project Consortium 2004). In conjunction with whole genome assemblies, this means that alignments of 30 Mbp of the human genome to the orthologous regions of a dozen or more mammalian genomes will soon be available. Comparative methodologies that can effectively exploit these data will provide a valuable source of annotation to complement other studies aimed at identifying functional elements and variants important to human biology and disease.
There are several major advantages to GERP that should make it a useful method for the annotation of constrained elements within deep mammalian sequence alignments. First, GERP is capable of coping with gaps with the simple, but effective strategy of ignoring them, which is important for the analysis of deep mammalian sequence alignments (>10 species, greater than two neutral substitutions per site). This feature will become critical with the expected availability of many draft and low-coverage mammalian genome sequences (http://www.genome.gov/10002154); these sequences, when aligned, will contain many gaps as a result of missing data. Second, rejected substitution scores can be used to compare and rank elements along a continuum reflective of the observed intensity of purifying selection to which they have been subjected. Finally, our null model requires no annotation or assumptions about the abundance of neutral DNA. This is an important feature in light of the known variability in constrained element density across the human genome (Cooper et al. 2004a). By using this model, we avoid the assumption that a particular fraction of bases in a locus (e.g., 5%) (Margulies et al. 2003) is under constraint, and instead obtain an actual estimate of the number of constrained bases.
Other studies have estimated the general impact of constraint on sequences in the human genome using an approach based on the comparison of “observed” and “expected” substitutions (Eyre-Walker and Keightley 1999; Keightley et al. 2005), similar to our use of “rejected substitutions” as a constraint metric. GERP shares conceptual roots with these studies, but applies them in a framework to identify regions of genomic sequence showing evidence of purifying selection at very high resolution. Use of more sophisticated models of nucleotide evolution for the generation of both “observed” and “expected” rates (Hwang and Green 2004; Siepel and Haussler 2004b) might eventually be used to improve the methodology, as the conceptual framework we have described is not dependent on the particulars of rate estimation.
In a sense, albeit oversimplified, “rejected substitutions” can be thought of as substitution events that “would” have occurred under neutrality, but were “rejected” due to the actions of purifying selection. There is no clear molecular evolutionary correlate to a “rejected substitution.” However, because the direct consequence of purifying selection is a reduction of substitution events, it is a useful term for the description of the strength of past constraints. RS scores are capable of capturing constraint at both high and low resolution, as no artificial length criteria are introduced; an element can achieve a high score with either weak constraint across many bases or strong constraint across a few bases. The concept of “rejected substitutions” thus provides a biologically motivated, yet statistically tractable framework for the detection and measurement of purifying selection in mammalian genomes.
Methods
Overview of the sequence data
Sequences corresponding to the genomic region encompassing the CFTR gene were generated from 28 nonhuman mammals. This represents an expanded version (involving more species) of the data described by Thomas et al. (2003), with all data and associated information available at http://www.nisc.nih.gov/data. The particular species are indicated in Figure 1B. The reference human sequence for this targeted region corresponds to NCBI build 35, i.e., human chromosome 7, 115404472–117281897. For all of our analyses, we treat the first human base in this region as position 1. This region contains 10 RefSeq genes, 40.2% repetitive DNA, and 38.4% G+C. Gene annotations for the human sequence were obtained from the UCSC Genome Browser (http://genome.ucsc.edu) using the RefSeq gene track (Pruitt and Maglott 2001); this includes 151 unique exons (in which an exon consisting of both UTR and coding sequence is split into separate “unique” exons) totaling 36,959 bases. Repetitive DNA was detected using RepeatMasker (http://www.repeatmasker.org), with ancestral repeats identified as previously described (Margulies et al. 2003).
Alignment
We used a combination of both global and local techniques to construct a multiple sequence alignment of these sequences. This strategy ensures that rearrangement events, identified as high-scoring local alignments, are properly captured and placed in the context of a global alignment. First, we compared each nonhuman sequence to the human using the program Shuffle-LAGAN (Brudno et al. 2003b). Shuffle-LAGAN is effective at the identification of rearrangements, such as translocations and inversions, in the context of a global, pairwise alignment. The nonhuman sequences are subsequently reordered and reoriented (i.e., shuffled) so that the local alignment chains are monotonic with respect to the human sequence. In this process, regions of the nonhuman sequences that lack detectable similarity to any region of the human are clipped and deleted. These rearranged sequences are thus orthologously collinear with the human sequence. We then aligned the rearranged sequences using MLAGAN, a global multiple sequence aligner previously shown to be effective and accurate for multiple alignment of mammalian genomic sequences (Brudno et al. 2003a). The tree supplied to MLAGAN for this step is similar to the topology shown in Figure 1B, but is rooted on the marsupial branch and includes a small number of topology changes designed to align longer branch groups later; this step is necessary because alignment accuracy is best when species with the greatest sequence similarity are aligned first. We used parameters similar to those used to generate alignments of the human, mouse, and rat genome sequences (Brudno et al. 2004).
Tree construction and estimation of the neutral rate
We extracted all of those regions from the uncompressed alignment corresponding to the highest-scoring constrained elements in the human sequence yielding an alignment of 97,274 columns. Using a species topology previously defined (Madsen et al. 2001; Murphy et al. 2001), we obtained the maximum likelihood branch lengths using SEMPHY (Friedman et al. 2002), with the HKY 85 model of nucleotide substitution (Hasegawa et al. 1985; Fig. 1B).
Given the relative branch-length tree (Fig. 1B), we estimated the neutral rate for the entire tree essentially as previously described (Cooper et al. 2003). Briefly, we estimate the neutral divergence among closely related species (ranging from 3% to 10% difference; Table 3), and subsequently extrapolated these rate estimates over the entire relative branch-length tree. As a source of aligned neutral DNA, we began with the uncompressed global alignment and excluded all of those alignment regions containing unambiguously constrained elements in the human sequence (the complement of the alignment used to determine the relative branch-length tree above). Divergence estimates were then made for each closely related group of species (neutral rate between 0.03 and 0.10 subs/site) using baseml of the PAML (Yang 1997) software package with the HKY 85 model of nucleotide substitution (Hasegawa et al. 1985). Gapped columns are eliminated in this procedure. The resultant estimates range from 3.17 to 4.66 neutral subs/site, with an average of 3.85 (Table 3). Except for those analyses that explicitly state otherwise (Fig. 2; “+” and “–” plots), all of the analyses described used the average estimate of 3.85 subs/site.
Table 3.
Neutral rate estimates of the entire analyzed tree
| Species | Neutral rate | Tree fraction | Neutral tree length |
|---|---|---|---|
| Baboon, Macaque, Vervet | 0.036 | 0.009 | 4.052 |
| Lemur, Mouse Lemur | 0.095 | 0.020 | 4.658 |
| Human, Chimpanzee, Gorilla, Orangutan | 0.047 | 0.015 | 3.173 |
| Cow, Sheep, Indian Muntjak | 0.097 | 0.028 | 3.500 |
| Average: | 3.846 |
Constrained element identification
GERP has several required inputs, e.g., a global multiple-sequence alignment, aligning as accurately as possible the orthologous bases from each species; a species tree with branch lengths, which provides relative estimates of the contribution, in terms of neutral divergence, for each species/ancestral lineage along the tree relating the species (Fig. 1B); and a neutral rate that estimates the total number of neutral subs/site captured by the tree (Table 3). The alignment is compressed such that a specified lead sequence, in our case the human sequence, is ungapped. This ensures consistency between alignment and annotation coordinates, allowing for direct comparison of constrained element annotations to other sequence features, such as exons and repeats.
After compressing the global alignment so that the human sequence is ungapped, the maximum likelihood rate estimate for each column was obtained using the program SEMPHY (Friedman et al. 2002). In this procedure, the likelihood is maximized with respect to all branch lengths in the topology relating the analyzed species, and the maximum likelihood estimate of the column's expected substitution count is treated as the “observed” value. We used the HKY85 (Hasegawa et al. 1985) model of nucleotide evolution (alternative realistic models have negligible impacts on the results) and the topology described in Figure 1B. Concomitant with this, “expected” rates of evolution were obtained for each column by pruning the neutral tree to eliminate gapped species, and determining the sum of the residual branch lengths (Fig. 1). We ignored columns for which the expected rate is <0.5 neutral subs/site, that is, after elimination of gapped sequences, the residual branch lengths of the neutral tree (Fig. 1B) sum to <0.5. Approximately 400,000 columns were ignored due to this step, the vast majority of which occur in large blocks corresponding to missing data for many species (especially at either end of the locus).
The alignment is thus associated with two vectors, one describing observed rates of evolution and another describing expected rates of evolution under neutrality, where observed and expected are defined as described above. Candidate constrained elements are discovered by identifying stretches of alignment positions that exhibit ratios of observed to expected rates below a certain threshold. For example, a threshold of unity permits only sites in which the observed rate is less than the expected rate (Fig. 1A). Note that decreasing the observed-to-expected ratio threshold increases the stringency at which elements are found, producing fewer, smaller elements that have higher scores perbase. As some functional elements are known to contain unconstrained or very weakly constrained bases, we allow candidate elements to be merged across a small number of intervening bases that do not meet the ratio criterion (“merging tolerance”). Candidate-constrained elements discovered in this manner are uniquely identified by a given ratio threshold and merging tolerance. These candidates are scored as the sum of the individual site differences between the observed and expected rates, a quantity that we term “rejected substitutions” (Fig. 1A). We subsequently eliminate all of those candidates that fail to meet a given RS threshold, and interpret the remainder to be legitimately constrained elements. Unconstrained columns are penalized in the scoring of the candidate element based upon their deviation above the expected rate. The maximum penalty is set at three times the neutral rate, and columns for which no observed rate was estimated are penalized by three times the total tree neutral rate.
Most of the results presented are based upon the identification of candidate constrained elements using an observed-to-expected ratio threshold of 1, and a merging tolerance of one column. All of the constrained elements we describe are significant at a confidence level of ∼95% (see Fig. 2). To enrich for smaller elements that score higher per-base, we use an observed-to-expected threshold of 0. Alternatively, to identify larger and cumulatively higher scoring elements, we increase the merging tolerance to six columns (Table 2); increasing beyond this number results in a significant loss of constrained element detection power due to the presence of too many unconstrained (and therefore penalized) bases among the otherwise significantly constrained elements (see Supplemental Table 1). To identify the large nonexonic constrained regions that overlap coding exons (Fig. 4B), we simply ignored positions in the alignment within coding exons. That is, they contributed neither positively nor negatively to the scoring of constrained elements, allowing a constrained element to overlap a coding exon without affecting its score.
We are making freely available a bundle of Perl scripts, along with documentation, to facilitate the methodology presented at http://mendel.stanford.edu/sidowlab/downloads.html. These scripts attempt to automate much of the process described above, and make calls to MLAGAN (Brudno et al. 2003a) and SEMPHY (Friedman et al. 2002) for alignment and rate estimation, respectively. It would be straightforward to replace MLAGAN if desired. We have also written a freely available Java application for the visualization and interactive browsing of multiple-sequence alignment data known as the Application for Browsing Constraints (ABC; http://mendel.stanford.edu/sidowlab/downloads.html; Cooper et al. 2004b).
False positive rates
We model the false discovery process by analyzing randomly generated permutations of the real alignment. Constrained elements identified in these permuted alignments represent artifacts of the discovery process, and are a function of the gross distributions of observed and expected rates of evolution. We generated 10 independent permutations of the alignment using the Matlab function “randperm.” Excluded from these permuted alignments are columns residing in alignment blocks for which no observed substitution rate estimate was obtained (see above), since constrained elements are not identified in these regions in the actual alignment either. Additionally, as we are interested in assessing the false discovery rate in neutral, or primarily neutral DNA, we excluded those alignment columns that reside within an unambiguously constrained region, defined by those constrained elements scoring 25 RS or greater. Approximately 50,000 alignment columns were excluded in this manner. Small, but significant increases in false discovery rate estimates are observed if these columns are retained (see Supplemental Figure 2). The confidence estimates for a given RS threshold (Fig. 2B) are determined as the number of constrained element bases identified in the real alignment, divided by the sum of constrained element bases in the real alignment and the average number of constrained bases identified in the 10 permuted alignments. For example, if, at a given threshold, there are 100,000 constrained element bases in the actual alignment and the average number of constrained bases in the permuted alignments is 5000, our confidence estimate for that threshold would be 100,000/(100,000 + 5000), or 95.2%.
Constrained element clustering
Regional densities of constrained and repetitive elements were determined using consecutive, nonoverlapping windows of 25-kb in width across the length of the human sequence (Fig. 3). The correlation between repeat and constrained element density was evaluated using a simple linear regression model, treating the density values of each 25-kb window as an independent data point (Fig. 3B). To determine the density of constrained elements near exons, repeats, and constrained elements (Fig. 3C), the percentage of bases within constrained elements was determined at each specified distance from these features. For example, 33% (Fig. 3C, _y_-axis) of bases that are exactly 10 bp away (Fig. 3C, _x_-axis) from an exon are within a constrained element.
Ultraconserved elements
To identify ultraconserved elements (Table 2), we normalized the RS score for each constrained element by the average neutral rate of the columns it contains, where constrained elements are identified using a merging tolerance of six unconstrained columns. All of those elements that score >200 RS per each unit of neutral rate (1 subs/site; equivalent to the previous definition of 130 RS for a neutral rate of 0.65 subs/site [Bejerano et al. 2004]) were retained. Each of these elements was compared with the chicken genome, downloaded from UCSC (http://genome.ucsc.edu), using WU-BLAST (W. Gish, 1996–2004, http://blast.wustl.edu) with a word size of 9, topcomboN=1, and all other parameters left at default. All reported chicken matches have expect scores smaller than e-10, and are reported based on the sum of the lengths of the HSPs and the overall percent identity of the HSP alignments (Table 2).
Acknowledgments
G.M.C. is a Howard Hughes Medical Institute pre-doctoral fellow. E.A.S. acknowledges support from the Stanford genome training program. A.S. acknowledges financial support from the NIH/NHGRI. We thank all members of the NISC Comparative Sequencing Program for their contributions, in particular its senior leadership (Drs. Bob Blakesley, Gerry Bouffard, Pam Thomas, Jenny McDowell, Bashali Maskeri, Nancy Hanson, Matt Portnoy, and Elliott Margulies). We thank Mukund Sundararajan, Michael Brudno, and Chuong Do for technical help with alignment tools, and members of the Sidow lab for helpful discussions. Finally, the detailed comments of three anonymous reviewers significantly improved this manuscript.
Article and publication are at http://www.genome.org/cgi/doi/10.1101/gr.3577405\. Article published online before print in June 2005.
Footnotes
[Supplemental material is available online at www.genome.org and http://mendel.stanford.edu/supplementarydata/. Original sequence data is available at http://www.nisc.nih.gov/data/.\]
References
- Aparicio, S., Chapman, J., Stupka, E., Putnam, N., Chia, J.M., Dehal, P., Christoffels, A., Rash, S., Hoon, S., Smit, A., et al. 2002. Whole-genome shotgun assembly and analysis of the genome of Fugu rubripes. Science 297**:** 1301-1310. [DOI] [PubMed] [Google Scholar]
- Arnone, M.I. and Davidson, E.H. 1997. The hardwiring of development: Organization and function of genomic regulatory systems. Development 124**:** 1851-1864. [DOI] [PubMed] [Google Scholar]
- Bejerano, G., Pheasant, M., Makunin, I., Stephen, S., Kent, W.J., Mattick, J.S., and Haussler, D. 2004. Ultraconserved elements in the human genome. Science 304**:** 1321-1325. [DOI] [PubMed] [Google Scholar]
- Berman, B.P., Nibu, Y., Pfeiffer, B.D., Tomancak, P., Celniker, S.E., Levine, M., Rubin, G.M., and Eisen, M.B. 2002. Exploiting transcription factor binding site clustering to identify _cis_-regulatory modules involved in pattern formation in the Drosophila genome. Proc. Natl. Acad. Sci. 99**:** 757-762. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Blakesley, R.W., Hansen, N.F., Mullikin, J.C., Thomas, P.J., McDowell, J.C., Maskeri, B., Young, A.C., Benjamin, B., Brooks, S.Y., Coleman, B.I., et al. 2004. An intermediate grade of finished genomic sequence suitable for comparative analyses. Genome Res. 14**:** 2235-2244. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Boffelli, D., McAuliffe, J., Ovcharenko, D., Lewis, K.D., Ovcharenko, I., Pachter, L., and Rubin, E.M. 2003. Phylogenetic shadowing of primate sequences to find functional regions of the human genome. Science 299**:** 1391-1394. [DOI] [PubMed] [Google Scholar]
- Botstein, D. and Risch, N. 2003. Discovering genotypes underlying human phenotypes: Past successes for mendelian disease, future approaches for complex disease. Nat. Genet. 33**:** 228-237. [DOI] [PubMed] [Google Scholar]
- Britten, R.J. 1997. Mobile elements inserted in the distant past have taken on important functions. Gene 205**:** 177-182. [DOI] [PubMed] [Google Scholar]
- Brudno, M., Do, C.B., Cooper, G.M., Kim, M.F., Davydov, E., Green, E.D., Sidow, A., and Batzoglou, S. 2003a. LAGAN and Multi-LAGAN: Efficient tools for large-scale multiple alignment of genomic DNA. Genome Res. 13**:** 721-731. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brudno, M., Malde, S., Poliakov, A., Do, C.B., Couronne, O., Dubchak, I., and Batzoglou, S. 2003b. Glocal alignment: Finding rearrangements during alignment. Bioinformatics 19**:** i54-i62. [DOI] [PubMed] [Google Scholar]
- Brudno, M., Poliakov, A., Salamov, A., Cooper, G.M., Sidow, A., Rubin, E.M., Solovyev, V., Batzoglou, S., and Dubchak, I. 2004. Automated whole-genome multiple alignment of rat, mouse, and human. Genome Res. 14**:** 685-692. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brugger, S.M., Merrill, A.E., Torres-Vazquez, J., Wu, N., Ting, M.C., Cho, J.Y., Dobias, S.L., Yi, S.E., Lyons, K., Bell, J.R., et al. 2004. A phylogenetically conserved _cis_-regulatory module in the Msx2 promoter is sufficient for BMP-dependent transcription in murine and Drosophila embryos. Development 131**:** 5153-5165. [DOI] [PubMed] [Google Scholar]
- Chang-Yeh, A., Mold, D.E., and Huang, R.C. 1991. Identification of a novel murine IAP-promoted placenta-expressed gene. Nucleic Acids Res. 19**:** 3667-3672. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Collins, F.S., Green, E.D., Guttmacher, A.E., and Guyer, M.S. 2003. A vision for the future of genomics research. Nature 422**:** 835-847. [DOI] [PubMed] [Google Scholar]
- Cooper, G.M. and Sidow, A. 2003. Genomic regulatory regions: Insights from comparative sequence analysis. Curr. Opin. Genet. Dev. 13**:** 604-610. [DOI] [PubMed] [Google Scholar]
- Cooper, G.M., Brudno, M., Green, E.D., Batzoglou, S., and Sidow, A. 2003. Quantitative estimates of sequence divergence for comparative analyses of mammalian genomes. Genome Res. 13**:** 813-820. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cooper, G.M., Brudno, M., Stone, E.A., Dubchak, I., Batzoglou, S., and Sidow, A. 2004a. Characterization of evolutionary rates and constraints in three Mammalian genomes. Genome Res. 14**:** 539-548. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cooper, G.M., Singaravelu, S.A., and Sidow, A. 2004b. ABC: Software for interactive browsing of genomic multiple sequence alignment data. BMC Bioinform. 5**:** 192. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dermitzakis, E.T., Reymond, A., Lyle, R., Scamuffa, N., Ucla, C., Deutsch, S., Stevenson, B.J., Flegel, V., Bucher, P., Jongeneel, C.V., et al. 2002. Numerous potentially functional but non-genic conserved sequences on human chromosome 21. Nature 420**:** 578-582. [DOI] [PubMed] [Google Scholar]
- Dermitzakis, E.T., Reymond, A., Scamuffa, N., Ucla, C., Kirkness, E., Rossier, C., and Antonarakis, S.E. 2003. Evolutionary discrimination of mammalian conserved non-genic sequences (CNGs). Science 302**:** 1033-1035. [DOI] [PubMed] [Google Scholar]
- Dubchak, I., Brudno, M., Loots, G.G., Pachter, L., Mayor, C., Rubin, E.M., and Frazer, K.A. 2000. Active conservation of noncoding sequences revealed by three-way species comparisons. Genome Res. 10**:** 1304-1306. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ellegren, H., Smith, N.G., and Webster, M.T. 2003. Mutation rate variation in the mammalian genome. Curr. Opin. Genet. Dev. 13**:** 562-568. [DOI] [PubMed] [Google Scholar]
- The ENCODE Project Consortium. 2004. The ENCODE (ENCyclopedia Of DNA Elements) Project. Science 306**:** 636-640. [DOI] [PubMed] [Google Scholar]
- Eyre-Walker, A. and Keightley, P.D. 1999. High genomic deleterious mutation rates in hominids. Nature 397**:** 344-347. [DOI] [PubMed] [Google Scholar]
- Friedman, N., Ninio, M., Pe'er, I., and Pupko, T. 2002. A structural EM algorithm for phylogenetic inference. J. Comput. Biol. 9**:** 331-353. [DOI] [PubMed] [Google Scholar]
- Ghanem, N., Jarinova, O., Amores, A., Long, Q., Hatch, G., Park, B.K., Rubenstein, J.L., and Ekker, M. 2003. Regulatory roles of conserved intergenic domains in vertebrate Dlx bigene clusters. Genome Res. 13**:** 533-543. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Göttgens, B., Barton, L.M., Chapman, M.A., Sinclair, A.M., Knudsen, B., Grafham, D., Gilbert, J.G., Rogers, J., Bentley, D.R., and Green, A.R. 2002. Transcriptional regulation of the stem cell leukemia gene (SCL)—comparative analysis of five vertebrate SCL loci. Genome Res. 12**:** 749-759. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gumucio, D.L., Heilstedt-Williamson, H., Gray, T.A., Tarle, S.A., Shelton, D.A., Tagle, D.A., Slightom, J.L., Goodman, M., and Collins, F.S. 1992. Phylogenetic footprinting reveals a nuclear protein which binds to silencer sequences in the human γ and ε globin genes. Mol. Cell. Biol. 12**:** 4919-4929. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hardison, R.C. 2000. Conserved noncoding sequences are reliable guides to regulatory elements. Trends Genet. 16**:** 369-372. [DOI] [PubMed] [Google Scholar]
- Hardison, R.C., Roskin, K.M., Yang, S., Diekhans, M., Kent, W.J., Weber, R., Elnitski, L., Li, J., O'Connor, M., Kolbe, D., et al. 2003. Covariation in frequencies of substitution, deletion, transposition, and recombination during eutherian evolution. Genome Res. 13**:** 13-26. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hart, M.C., Korshunova, Y.O., and Cooper, J.A. 1997. Vertebrates have conserved capping protein α isoforms with specific expression patterns. Cell. Motil. Cytoskeleton 38**:** 120-132. [DOI] [PubMed] [Google Scholar]
- Hasegawa, M., Kishino, H., and Yano, T. 1985. Dating of the human–ape splitting by a molecular clock of mitochondrial DNA. J. Mol. Evol. 22**:** 160-174. [DOI] [PubMed] [Google Scholar]
- Hillier, L.W., Miller, W., Birney, E., Warren, W., Hardison, R.C., Ponting, C.P., Bork, P., Burt, D.W., Groenen, M.A., Delany, M.E., et al. 2004. Sequence and comparative analysis of the chicken genome provide unique perspectives on vertebrate evolution. Nature 432**:** 695-716. [DOI] [PubMed] [Google Scholar]
- Hwang, D.G. and Green, P. 2004. Bayesian Markov chain Monte Carlo sequence analysis reveals varying neutral substitution patterns in mammalian evolution. Proc. Natl. Acad. Sci. 101**:** 13994-14001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jordan, I.K., Rogozin, I.B., Glazko, G.V., and Koonin, E.V. 2003. Origin of a substantial fraction of human regulatory sequences from transposable elements. Trends Genet. 19**:** 68-72. [DOI] [PubMed] [Google Scholar]
- Keightley, P.D., Lercher, M.J., and Eyre-Walker, A. 2005. Evidence for widespread degradation of gene control regions in hominid genomes. PLoS Biol. 3**:** e42. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Khambata-Ford, S., Liu, Y., Gleason, C., Dickson, M., Altman, R.B., Batzoglou, S., and Myers, R.M. 2003. Identification of promoter regions in the human genome by using a retroviral plasmid library-based functional reporter gene assay. Genome Res. 13**:** 1765-1774. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kimura, M. 1983. The neutral theory of molecular evolution. Cambridge University Press, Cambridge, New York.
- Li, W.-H. 1997. Molecular evolution. Sinauer Associates, Sunderland, MA.
- Madsen, O., Scally, M., Douady, C.J., Kao, D.J., DeBry, R.W., Adkins, R., Amrine, H.M., Stanhope, M.J., de Jong, W.W., and Springer, M.S. 2001. Parallel adaptive radiations in two major clades of placental mammals. Nature 409**:** 610-614. [DOI] [PubMed] [Google Scholar]
- Margulies, E.H., Blanchette, M., Haussler, D., and Green, E.D. 2003. Identification and characterization of multi-species conserved sequences. Genome Res. 13**:** 2507-2518. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Markstein, M., Markstein, P., Markstein, V., and Levine, M.S. 2002. Genome-wide analysis of clustered Dorsal binding sites identifies putative target genes in the Drosophila embryo. Proc. Natl. Acad. Sci. 99**:** 763-768. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mayor, C., Brudno, M., Schwartz, J.R., Poliakov, A., Rubin, E.M., Frazer, K.A., Pachter, L.S., and Dubchak, I. 2000. VISTA: Visualizing global DNA sequence alignments of arbitrary length. Bioinformatics 16**:** 1046-1047. [DOI] [PubMed] [Google Scholar]
- Mouse Genome Sequencing Consortium. 2002. Initial sequencing and comparative analysis of the mouse genome. Nature 420**:** 520-562. [DOI] [PubMed] [Google Scholar]
- Murphy, W.J., Eizirik, E., Johnson, W.E., Zhang, Y.P., Ryder, O.A., and O'Brien, S.J. 2001. Molecular phylogenetics and the origins of placental mammals. Nature 409**:** 614-618. [DOI] [PubMed] [Google Scholar]
- Nekrutenko, A. and Li, W.H. 2001. Transposable elements are found in a large number of human protein-coding genes. Trends Genet. 17**:** 619-621. [DOI] [PubMed] [Google Scholar]
- Nobrega, M.A., Ovcharenko, I., Afzal, V., and Rubin, E.M. 2003. Scanning human gene deserts for long-range enhancers. Science 302**:** 413. [DOI] [PubMed] [Google Scholar]
- O'Brien, S.J., Menotti-Raymond, M., Murphy, W.J., Nash, W.G., Wienberg, J., Stanyon, R., Copeland, N.G., Jenkins, N.A., Womack, J.E., and Marshall Graves, J.A. 1999. The promise of comparative genomics in mammals. Science 286**:** 458-462, 479-481. [DOI] [PubMed] [Google Scholar]
- Peaston, A.E., Evsikov, A.V., Graber, J.H., de Vries, W.N., Holbrook, A.E., Solter, D., and Knowles, B.B. 2004. Retrotransposons regulate host genes in mouse oocytes and preimplantation embryos. Dev. Cell 7**:** 597-606. [DOI] [PubMed] [Google Scholar]
- Pennacchio, L.A. and Rubin, E.M. 2001. Genomic strategies to identify mammalian regulatory sequences. Nat. Rev. Genet. 2**:** 100-109. [DOI] [PubMed] [Google Scholar]
- Pennacchio, L.A., Olivier, M., Hubacek, J.A., Cohen, J.C., Cox, D.R., Fruchart, J.C., Krauss, R.M., and Rubin, E.M. 2001. An apolipoprotein influencing triglycerides in humans and mice revealed by comparative sequencing. Science 294**:** 169-173. [DOI] [PubMed] [Google Scholar]
- Pruitt, K.D. and Maglott, D.R. 2001. RefSeq and LocusLink: NCBI gene-centered resources. Nucleic Acids Res. 29**:** 137-140. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rat Genome Sequencing Project Consortium. 2004. Genome sequence of the Brown Norway rat yields insights into mammalian evolution. Nature 428**:** 493-521. [DOI] [PubMed] [Google Scholar]
- Shah, N., Couronne, O., Pennacchio, L.A., Brudno, M., Batzoglou, S., Bethel, E.W., Rubin, E.M., Hamann, B., and Dubchak, I. 2004. Phylo-VISTA: Interactive visualization of multiple DNA sequence alignments. Bioinformatics 20**:** 636-643. [DOI] [PubMed] [Google Scholar]
- Siepel, A. and Haussler, D. 2004a. Combining phylogenetic and hidden Markov models in biosequence analysis. J. Comput. Biol. 11**:** 413-428. [DOI] [PubMed] [Google Scholar]
- ———. 2004b. Phylogenetic estimation of context-dependent substitution rates by maximum likelihood. Mol. Biol. Evol. 21**:** 468-488. [DOI] [PubMed] [Google Scholar]
- Silva, J.C., Shabalina, S.A., Harris, D.G., Spouge, J.L., and Kondrashovi, A.S. 2003. Conserved fragments of transposable elements in intergenic regions: Evidence for widespread recruitment of MIR- and L2-derived sequences within the mouse and human genomes. Genet. Res. 82**:** 1-18. [DOI] [PubMed] [Google Scholar]
- Sorek, R. and Ast, G. 2003. Intronic sequences flanking alternatively spliced exons are conserved between human and mouse. Genome Res. 13**:** 1631-1637. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sumiyama, K., Kim, C.B., and Ruddle, F.H. 2001. An efficient _cis_-element discovery method using multiple sequence comparisons based on evolutionary relationships. Genomics 71**:** 260-262. [DOI] [PubMed] [Google Scholar]
- Thomas, J.W., Touchman, J.W., Blakesley, R.W., Bouffard, G.G., Beckstrom-Sternberg, S.M., Margulies, E.H., Blanchette, M., Siepel, A.C., Thomas, P.J., McDowell, J.C., et al. 2003. Comparative analyses of multi-species sequences from targeted genomic regions. Nature 424**:** 788-793. [DOI] [PubMed] [Google Scholar]
- Woolfe, A., Goodson, M., Goode, D.K., Snell, P., McEwen, G.K., Vavouri, T., Smith, S.F., North, P., Callaway, H., Kelly, K., et al. 2004. Highly conserved non-coding sequences are associated with vertebrate development. PLoS Biol. 3**:** e7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yang, Z. 1997. PAML: A program package for phylogenetic analysis by maximum likelihood. CABIOS 13**:** 555-556. [DOI] [PubMed] [Google Scholar]
- Yang, S., Smit, A.F., Schwartz, S., Chiaromonte, F., Roskin, K.M., Haussler, D., Miller, W., and Hardison, R.C. 2004. Patterns of insertions and their covariation with substitutions in the rat, mouse, and human genomes. Genome Res. 14**:** 517-527. [DOI] [PMC free article] [PubMed] [Google Scholar]
Web site references
- http://blast.wustl.edu; WU-BLAST homepage.
- http://www.repeatmasker.org; RepeatMasker homepage.
- http://mendel.stanford.edu/sidowlab; Sidow Lab homepage.
- http://genome.ucsc.edu; UCSC Genome Browser homepage.
- http://www.nisc.nih.gov/data; NISC Comparative Sequencing Program homepage.
- http://www.genome.gov/10002154; NHGRI Genome Sequencing Proposals.