A Powerful and Robust Method for Mapping Quantitative Trait Loci in General Pedigrees (original) (raw)
Abstract
The variance-components model is the method of choice for mapping quantitative trait loci in general human pedigrees. This model assumes normally distributed trait values and includes a major gene effect, random polygenic and environmental effects, and covariate effects. Violation of the normality assumption has detrimental effects on the type I error and power. One possible way of achieving normality is to transform trait values. The true transformation is unknown in practice, and different transformations may yield conflicting results. In addition, the commonly used transformations are ineffective in dealing with outlying trait values. We propose a novel extension of the variance-components model that allows the true transformation function to be completely unspecified. We present efficient likelihood-based procedures to estimate variance components and to test for genetic linkage. Simulation studies demonstrated that the new method is as powerful as the existing variance-components methods when the normality assumption holds; when the normality assumption fails, the new method still provides accurate control of type I error and is substantially more powerful than the existing methods. We performed a genomewide scan of monoamine oxidase B for the Collaborative Study on the Genetics of Alcoholism. In that study, the results that are based on the existing variance-components method changed dramatically when three outlying trait values were excluded from the analysis, whereas our method yielded essentially the same answers with or without those three outliers. The computer program that implements the new method is freely available.
Introduction
Mapping genes associated with various traits and diseases is one of the most important research areas in human genetics. A major effort in the gene-mapping process is the detection of loci that influence quantitative traits, which are referred to as “quantitative trait loci” (QTLs). Because complex diseases are associated with complex traits, many of which are quantitative, QTL analysis plays a critical role in the genetic dissection of complex human diseases. The recent explosion in genetic mapping data has placed a premium on the development of statistical methods for mapping QTLs (Pratt et al. 2000). Feingold (2001, 2002) provided excellent reviews of QTL-mapping methods, all of which are based on the principle that family members who have similar trait values should have higher-than-expected levels of identity-by-descent (IBD) allele sharing near the genes that influence those traits.
The simplest QTL-mapping method is Haseman-Elston (1972) regression, which regresses the squared differences in the trait values of sib pairs on their IBD sharing at a putative locus. Several groups (Wright 1997; Drigalenko 1998; Elston et al. 2000; Xu et al. 2000; Forrest 2001; Sham and Purcell 2001; Visscher and Hopper 2001) have attempted to improve the power of this regression by use of both the squared trait sum and the squared trait difference, whereas others (Tang and Siegmund 2001; Putter et al. 2002; Wang and Huang 2002) have proposed score statistics with similar properties. All these methods are limited to sibships or, in many cases, to sib pairs. Sham et al. (2002) offered a regression method for extended pedigrees. The idea is to reverse the Haseman-Elston paradigm by regressing the IBD sharing on an appropriate function of the trait values. This method requires specification of the correlation for each type of relative pair and does not accommodate covariate effects, gene-environment interactions, epistasis, or pleiotropy. Its type I error is inflated in some circumstances. Chiou et al. (2005) proposed to estimate the probability that a sib pair shares the same allele at the trait locus as a nonparametric function of the trait values.
An alternative approach is the variance-components model (Goldgar 1990; Schork 1993; Amos 1994; Fulker et al. 1995; Almasy and Blangero 1998; Pratt et al. 2000). This model decomposes the overall phenotypic variability among individuals within pedigrees into fixed effects due to observed covariates, random effects due to an unobserved trait-affecting major locus, random polygenic effects, and residual nongenetic variance. The analysis is typically based on maximum-likelihood estimation. This approach is applicable to any type of pedigree and has substantially higher power than Haseman-Elston and related methods (Amos et al. 1996; Williams et al. 1997; Almasy and Blangero 1998; Pratt et al. 2000; Forrest 2001; Tang and Siegmund 2001; Feingold 2001, 2002). “It has superseded Haseman-Elston as the method of choice for most studies, particularly when large pedigrees are used” (Feingold 2002, p. 217).
The variance-components model assumes that the trait values of family members follow a multivariate normal distribution. When this assumption is violated, the parameter estimators can be severely biased, the type I error can be substantially inflated, and the power can be drastically reduced (Amos et al. 1996; Allison et al. 1999; Tang and Siegmund 2001; Feingold 2001, 2002). In this sense, the variance-components approach is less robust than Haseman-Elston regression (Allison et al. 2000). When there is nonnormality, one strategy is to perform a parametric transformation, such as the log transformation or square-root transformation on the trait values to approximate normality (Allison et al. 2000; Geller et al. 2003; Strug et al. 2003). It is often difficult to find an appropriate transformation, especially when there are negative trait values, and different transformations may yield conflicting results. Incorrect transformations will cause biased parameter estimators, inflated type I error, and loss of power. Furthermore, parametric transformations are not effective in handling outlying trait values, which can create spurious linkage signals.
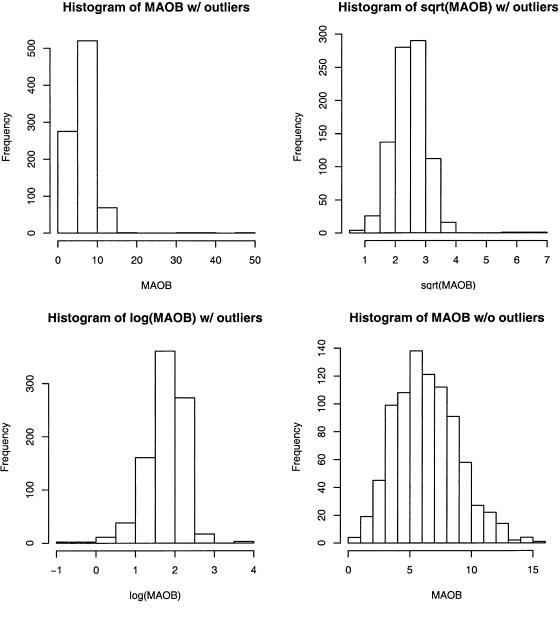
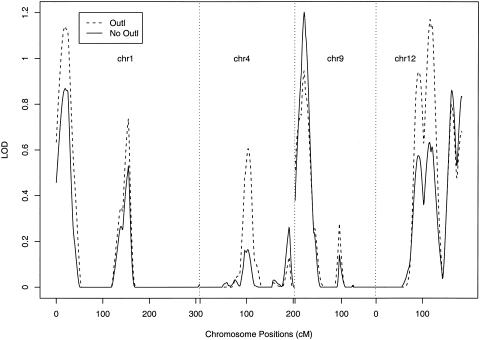
Figure 1 plots the LOD scores for the variance-components analysis of monoamine oxidase B (MAOB) from the Collaborative Study on the Genetics of Alcoholism (COGA), which is a multicenter study for identification of genes that cause alcohol dependence (Begleiter et al. 1995). MAOB is a mitochondrial enzyme whose measurement is positive and can be large. The original analysis showed significant evidence of linkage on chromosomes 1, 4, 9, and 12. Three members in a family had unusually large MAOB values. When those three individuals were removed from the analysis, the evidence of linkage completely disappeared. This kind of phenomenon has deterred human geneticists from performing QTL analysis (Allison et al. 1999).
Figure 1.
Multipoint LOD scores from the existing variance-components method for chromosomes 1, 4, 9, and 12 in the COGA study. Outl = outliers included; No Outl = outliers excluded.
A question naturally arises as to whether there exists a method that retains the robustness of Haseman-Elston regression while approaching the greater power of the variance components model (Feingold 2001). The present article provides a positive answer to this question. We propose a novel modification of the variance-components model to allow a completely arbitrary transformation function of trait values. We then derive maximum-likelihood estimators of variance components and construct likelihood-ratio statistics for testing the existence of QTLs at arbitrary locations along the genome. We implement the new method in a free computer program. Extensive simulation studies demonstrate that our new method is as efficient as the existing variance-component methods when the normality assumption holds; under nonnormality, the new method continues to have proper type I error and good power, whereas the existing methods have inflated type I error and diminished power. Unlike existing methods, the new method is insensitive to outliers. The application of the new method to the aforementioned COGA data resolved the dilemma caused by the three outlying observations.
Material and Methods
Consider n general pedigrees or families and n i relatives in the _i_th family, _i_=1,…,n. Let Y ij denote the trait value for the _j_th relative of the _i_th family and X ij a vector of directly observable covariates. At each genome position to be examined, we consider a variance-components model that partitions the total phenotypic variance into components that are due to a major gene at the locus, other unlinked genes, covariates, and environmental factors:

where H is an unknown increasing function, β is a set of fixed effects, g ij is a random effect due to the major gene, G ij is a random effect due to other genes at unlinked loci, and e ij is an individual-specific residual environmental effect. The random effects are assumed to be normally distributed with mean 0 and variances σ2_g_, σ2_G_, and σ2_e_. Because H is an arbitrary function, we constrain the residual variance σ2_e_ to be 1, and we do not include an intercept in the model, since the intercept can be absorbed by H.
Assume that g ij, G ij, and e ij are not correlated. Then the total trait variance Var_[H(Y ij)] is σ2=σ2_g+σ2_G_+σ2_e_. The overall heritability of the trait is
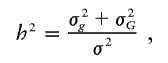
and the heritability attributable to the examined locus is
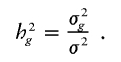
The genetic variances can be optionally decomposed into additive and dominant effects, with σ2_g_=σ2_ga_+σ2_gd_ and σ2_G_=σ2_Ga_+σ2_Gd_. We may include a household-specific random effect in the model, since the relatives in a household share the same environment. The model can also be easily extended to include interactions between different effects as well as multiple trait-affecting loci. For simplicity of description, we focus on equation (1).
We refer to equation (1) as a semiparametric linear transformation model with random effects or as semiparametric variance-components model because the true transformation function H is unspecified. By contrast, the existing variance-components model is parametric, because the transformation is assumed to be known or is implicitly incorporated in the definition of Y. Allowing an unknown transformation function is equivalent to allowing an arbitrary trait distribution, in that, for any distribution of Y, there always exists a transformation H such that H(Y) has the standard normal distribution. In this sense, equation (1) generalizes the existing variance-components model to allow an arbitrary trait distribution.
The trait covariance between any two pedigree members can be expressed as a weighted sum of the variance components
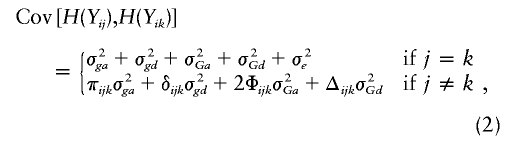
where π_ijk_ is the proportion of alleles at the major locus that are IBD in the j_th and k_th relatives of the i_th family, δ_ijk is the probability that both alleles at the locus are IBD, Φ_ijk is the kinship coefficient of relatives j and k, and Δ_ijk is the expected probability that the relatives share both alleles IBD. Note that π_ijk_ and δ_ijk_ are determined by the genotyping data, whereas Φ_ijk_ and Δ_ijk_ depend on only the degree of relatedness. We can infer the IBD allele–sharing probabilities at an arbitrary genome position by using the exact multipoint algorithm (Lander and Green 1987) implemented in GENEHUNTER (Kruglyak et al. 1996) or the approximation given in SOLAR (Almasy and Blangero 1998).
Write Λ(y)=e H(y). Let γ denote the variance parameters σ2_ga_, σ2_gd_, σ2_Ga_, σ2_Gd_, and σ2_e_, and let θ denote the parameters β, γ and Λ(·). The log likelihood for θ is given as
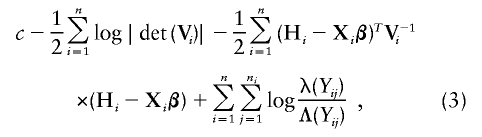
where c is a constant, X i is the matrix of covariates for the _i_th family, V i is the variance-covariance matrix of the _i_th family derived from equation (2), λ(·) is the derivative of Λ(·), and H i is the vector of [_log_Λ(Y _i_1),…,_log_Λ(Y in i)]. This is a nonparametric likelihood (Bickel et al. 1993), in that the function H(·) or Λ(·) is completely unspecified.
In the current variance-components literature, the transformation function H is assumed to be known, so that the log likelihood takes the form
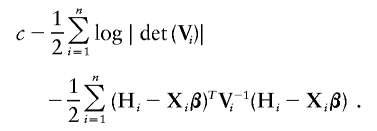
There are two key differences between this parametric log likelihood and the nonparametric log likelihood given in expression (3). First, the last term of expression (3) does not enter into the parametric log likelihood. Second, the values of H(Y ij) are known in the parametric log likelihood but are unknown function of the trait values in the nonparametric log likelihood.
We wish to estimate the finite-dimensional parameters β and γ, along with the infinite-dimensional parameter Λ(·), by maximizing the nonparametric log likelihood given in (3). The maximum of (3) is infinity if Λ(·) is restricted to be absolutely continuous, since we can always choose some function Λ(y) with fixed values at the Y ij while letting λ(Y ij) go to infinity. Thus, we allow Λ(·) to be right-continuous and maximize the function
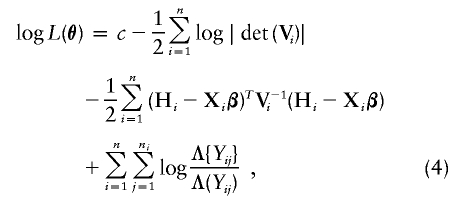
where Λ{Y ij} is the jump size of Λ(y) at _y_=Y ij; that is, the value of Λ(y) at _y_=Y ij minus its value right before Y ij. The resultant estimator, denoted by 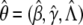 , is the maximum-likelihood estimator of θ or, more precisely, the nonparametric maximum-likelihood estimator (Bickel et al. 1993).
, is the maximum-likelihood estimator of θ or, more precisely, the nonparametric maximum-likelihood estimator (Bickel et al. 1993).
It can be shown that 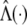 is a step function with jumps only at the observed values of Y ij. Thus,
is a step function with jumps only at the observed values of Y ij. Thus, 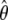 is obtained by maximizing (4) over β, γ, and Λ{Y ij} (_i_=1,…,n;_j_=1,…,n i). To ensure positive estimators for the jump sizes and variance parameters, we reparameterize Λ{Y ij} and γ as log(Λ{Y ij}) and log(γ) in the maximization. The maximization is realized via the quasi-Newton algorithm (Press et al. 1992). We chose the initial values of Λ{Y ij} in accordance with a common transformation, such as the log transformation. The first derivatives of (4) with respect to the unknown parameters are given in appendix A. In those expressions, the unknown parameters depend on the Y ij only through the ranks of the Y ij. This fact implies that the parameter estimators will remain the same if the trait values are replaced by their ranks. Thus, the proposed estimators are rank-based and hence robust to outliers. Note that the unknown transformation H(y) is estimated by
is obtained by maximizing (4) over β, γ, and Λ{Y ij} (_i_=1,…,n;_j_=1,…,n i). To ensure positive estimators for the jump sizes and variance parameters, we reparameterize Λ{Y ij} and γ as log(Λ{Y ij}) and log(γ) in the maximization. The maximization is realized via the quasi-Newton algorithm (Press et al. 1992). We chose the initial values of Λ{Y ij} in accordance with a common transformation, such as the log transformation. The first derivatives of (4) with respect to the unknown parameters are given in appendix A. In those expressions, the unknown parameters depend on the Y ij only through the ranks of the Y ij. This fact implies that the parameter estimators will remain the same if the trait values are replaced by their ranks. Thus, the proposed estimators are rank-based and hence robust to outliers. Note that the unknown transformation H(y) is estimated by 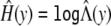 .
.
Although it is a nonparametric maximum-likelihood estimator, 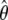 possesses the familiar asymptotic properties of a parametric maximum-likelihood estimator. Specifically,
possesses the familiar asymptotic properties of a parametric maximum-likelihood estimator. Specifically, 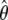 is consistent, asymptotically normal, and asymptotically efficient, and its covariance matrix can be estimated by the inversed Fisher information matrix of (4). The asymptotic efficiency implies that
is consistent, asymptotically normal, and asymptotically efficient, and its covariance matrix can be estimated by the inversed Fisher information matrix of (4). The asymptotic efficiency implies that 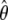 is the most efficient estimator among all valid estimators of θ, at least in large samples. The proofs of these results involve very advanced mathematical arguments. The interested readers are referred to appendix B of Lin (2004) for an outline of arguments for this kind of problem. The detailed proofs are available from the authors on request.
is the most efficient estimator among all valid estimators of θ, at least in large samples. The proofs of these results involve very advanced mathematical arguments. The interested readers are referred to appendix B of Lin (2004) for an outline of arguments for this kind of problem. The detailed proofs are available from the authors on request.
We can use the familiar maximum-likelihood statistics to make inferences about θ. In particular, we can perform various hypothesis tests according to the objectives of the linkage study at hand. For example, we can assess whether there is a major gene effect at the examined locus by testing the null hypothesis _H_0:σ2_ga_=σ2_gd_=0 against the alternative H A:σ2_ga_>0 or σ2_gd_>0. We can also test the null hypothesis of no additive major-gene effect, _H_0:σ2_ga_=0, or the null hypothesis of no polygenic effects, _H_0:σ2_Ga_=σ2_Gd_=0. For each hypothesis test, we can calculate the likelihood-ratio statistic at any position along the genome with
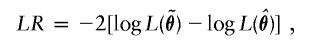
where 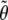 is the (restricted) maximum-likelihood estimator of θ under the null hypothesis. When we test a single variance component, the asymptotic distribution of the likelihood-ratio statistic is a half-and-half mixture of a χ21 variable and a point mass at 0 (Self and Liang 1987). When multiple variance components are tested, the likelihood-ratio statistic has a more complex asymptotic distribution that continues to be a mixture of χ2 distributions (Self and Liang 1987). The conventional LOD score is simply LR/4.6.
is the (restricted) maximum-likelihood estimator of θ under the null hypothesis. When we test a single variance component, the asymptotic distribution of the likelihood-ratio statistic is a half-and-half mixture of a χ21 variable and a point mass at 0 (Self and Liang 1987). When multiple variance components are tested, the likelihood-ratio statistic has a more complex asymptotic distribution that continues to be a mixture of χ2 distributions (Self and Liang 1987). The conventional LOD score is simply LR/4.6.
The proposed method is reminiscent of the well-known Cox (1972) regression analysis with survival data. In fact, the Cox proportional hazards model can be written as a semiparametric linear transformation model: H(Y)=β_T_ X+ε, where H is an unknown increasing function and ε has the standard extreme-value distribution. The nonparametric maximum-likelihood estimators of β and Λ(y)=e H(y) are exactly the familiar maximum partial-likelihood estimator of the relative risk and the Breslow (1972) estimator of the cumulative hazard function. It is well known that the maximum partial likelihood estimator is rank based, the Breslow estimator is a step function, and both estimators are statistically efficient. Our estimators of β and Λ have the same properties.
Results
COGA Study
COGA is a six-center study aimed to detect and map susceptibility genes for alcohol dependence and related phenotypes (Begleiter et al. 1995). The study involved 105 families (typically 3 or 4 generations) with a total of 1,214 members. The largest family size was 37. A total of 992 individuals were genotyped at 285 autosomal markers on 22 chromosomes, with an average intermarker distance of 13.5 cM. We considered the quantitative trait MAOB. MAOB is a mitochondrial enzyme involved in the degradation of certain neurotransmitter amines, specifically phenylethylamine and benzylamine. Low platelet MAOB activity has been found to be associated with alcoholism (Major and Murphy 1978; Sullivan et al. 1979).
Information on MAOB activity in platelets was available for 904 of the 1,214 individuals. The mean MAOB activity was 6.48, with an SD of 3.17 and a median value of 6.17. Three outliers for MAOB activity—with values of 33.18, 38.61, and 45.44—were clustered in a single family; the values for the remaining individuals in this family were 3.53 and 6.05. Figure 2 presents the histograms of MAOB values with and without the three outliers. With the outliers, the distribution is severely right skewed and highly leptokurtic, with skewness of 4.02 and kurtosis of 40.7, as opposed to skewness of only 0.41 and kurtosis of 0.01 without outliers. Of the 904 individuals with MAOB-activity information, 432 were male, with a mean value of 5.58 and a median value of 5.36, and 472 were female, with a mean value of 7.31 and a median value of 7.20. MAOB activity tended to be lower for smokers than for nonsmokers, with mean values of 5.61 versus 7.24 and median values of 5.20 versus 7.22, respectively. MAOB activity also varied by ethnicity, with mean values of 7.72, 6.17, and 7.15 and median values of 6.98, 5.87, and 7.04 for ethnic groups “black, non-Hispanic,” “white, non-Hispanic,” and “white, Hispanic,” respectively. We included age at interview, sex, ethnicity, and smoking status as covariates in our analysis.
Figure 2.
Histograms of MAOB activity in the COGA study
We calculated the IBD allele–sharing probabilities at the 1-cM increment along the genome by using the computer package SOLAR (Almasy and Blangero 1998). We first performed the genomewide linkage scan of MAOB activity using the existing variance-components method. As shown in figure 1, significant evidence in favor of linkage with MAOB activity was observed on chromosomes 1, 4, 9, and 12, with peak LOD scores of at least 6. The peak LOD score on chromosome 12 exceeded 12. When the three outliers were deleted, the evidence of linkage completely disappeared. These results are similar to those of Barnholtz et al. (1999), who used the SAGE FSP program to break up the data set into nuclear families and then used a modified version of GENEHUNTER (Kruglyak et al. 1996; Amos et al. 1997) to calculate the multipoint IBD values. Clearly, the existing method is highly sensitive to outliers in this case.
As is evident in figure 2, parametric transformations are ineffective in handling outliers. The distributions are right skewed under the square-root transformation and left skewed under the log transformation. The kurtosis values are 6.3 and 3.0 under the square-root and log transformations, respectively. Under the square-root transformation, the peak LOD scores for chromosomes 1, 4, 9, and 12 are 2.6, 3.24, 1.67, and 3.83, respectively. Under the log transformation, the corresponding peaks are 0.88, 1.08, 1.64, and 1.18. It is disconcerting that these two transformations have conflicting results.
We also applied the new method to the COGA data and displayed the results in figure 3. No linkage signals were detected, regardless of whether the outliers were included or excluded. The two sets of LOD curves were similar to each other, and no LOD scores were >1.2. The new method is less sensitive to the outliers, so the results should be more trustworthy.
Figure 3.
Multipoint LOD scores from the new method for chromosomes 1, 4, 9, and 12 in the COGA study. Outl = outliers included; No Outl = outliers excluded.
Simulation Studies
We conducted extensive simulation studies to evaluate the performance of the new method and to compare it with that of the existing methods. We generated trait values for sib trios from the model
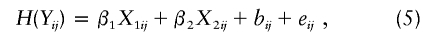
where β1=-0.5, β2=0.5,X_1_ij is a binary variable with 0.5 probability of being 1, X_2_ij is an independent standard normal variable, b ij consists of major gene and polygenic effects, and e ij is the residual random error. The covariates X_1_ij and X_2_ij represent sex and standardized age, respectively. We simulated a 100-cM chromosome with 51 equally spaced markers by Markov chain under the Haldane mapping function. Each marker consisted of four equally frequent alleles. A true QTL was placed at the center of the chromosome. For simplicity, we considered only additive genetic effects. We varied the variance parameters to yield different values of overall genetic heritability _h_2 and major-gene heritability h_2_g. In particular, we considered the following six scenarios.
| Model | σ2_g_ | σ2_G_ | σ2_e_ | h_2_g | _h_2 |
|---|---|---|---|---|---|
| a | .0 | 1.0 | 1.0 | .0 | .5 |
| b | .2 | .8 | 1.0 | .1 | .5 |
| c | .4 | .6 | 1.0 | .2 | .5 |
| d | .0 | .6 | 1.4 | .0 | .3 |
| e | .2 | .4 | 1.4 | .1 | .3 |
| f | .4 | .2 | 1.4 | .2 | .3 |
Scenarios a and d pertain to the null hypothesis, the others to alternative hypotheses. We considered 200 and 500 sib trios. For each setup, we simulated 10,000 data sets.
In the first series of studies, we generated U ij from the model
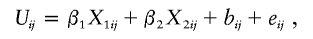
and set Y _ij_=_e_1+U ij+(5+U ij)2. The resulting data have an average kurtosis of 44.5. After the square-root and log transformations, the average kurtosis values are 5.82 and 4.83, respectively.
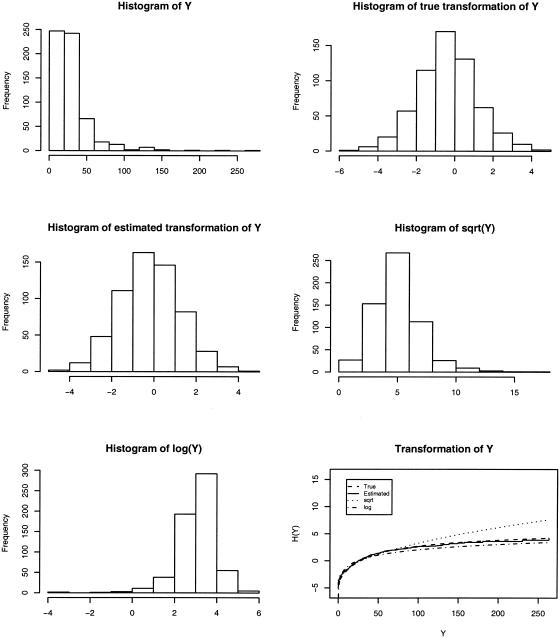
We analyzed the data in five different ways: the new method and the existing methods with true transformation, log transformation, square-root transformation, and no transformation. The existing method with the true transformation pertains to the ideal situation in which the normality assumption holds (after a known transformation). Figure 4 shows the distribution of trait values for the first simulated data set. Neither the log transformation nor the square-root transformation provided a good normal approximation. The transformation estimated by the new method is almost identical to the true transformation and approximated the normal distribution very well.
Figure 4.
Histograms of trait values under various transformations and plots of the true, square-root, log, and estimated transformations for a simulated data set with 200 sib trios.
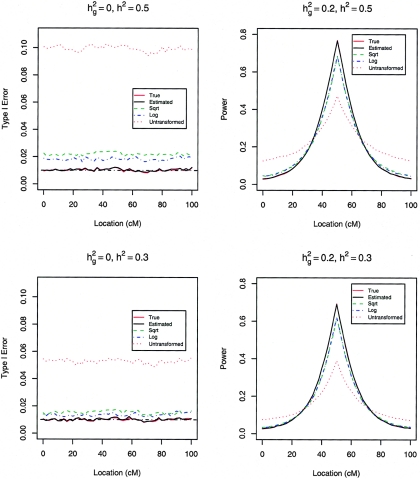
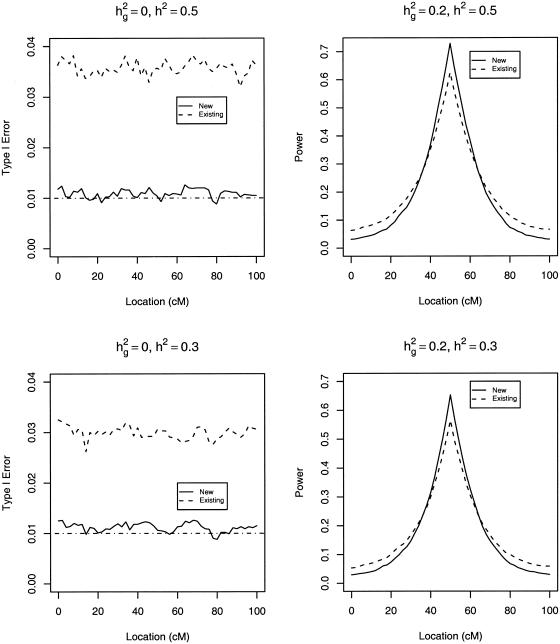
We assessed the performance of the likelihood-ratio statistics for testing _H_0:σ2_g_=0 versus H A:σ2_g_>0 at the nominal significance level α of 5%, 1%, and 0.1%. Table 1 presents the type I error and power at the true QTL with _n_=200, whereas figure 5 displays the results of the linkage scans on the whole chromosome at the 2-cM increment with _n_=500. The new method provides accurate control of type I error in all cases and has virtually the same power as the existing method with the true transformation. Thus, the new method performs as well as the parametric method under normality or with known transformation. Without transformation, the type I error of the existing method is very wrong. With the log or the square-root transformation, the type I error is still inflated. Although it has much smaller type I error than the existing methods, the new method tends to be more powerful than the existing methods with or without transformation, especially when there are strong genetic effects.
Table 1.
Type I Error and Power (%) of Likelihood-Ratio Tests under Nonnormality, with 200 Sib Trios
| Type I Error and Power (%) for | |||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Existing Methods | |||||||||||||||
| New Method | True | Square Root | Log | Untransformed | |||||||||||
| Model | α=5 | α=1 | α=.1 | α=5 | α=1 | α=.1 | α=5 | α=1 | α=.1 | α=5 | α=1 | α=.1 | α=5 | α=1 | α=.1 |
| a | 4.97 | .99 | .13 | 4.80 | .92 | .10 | 6.84 | 1.96 | .31 | 6.42 | 1.68 | .29 | 14.71 | 7.39 | 3.37 |
| b | 24.43 | 8.69 | 1.73 | 24.60 | 8.58 | 1.66 | 24.48 | 10.06 | 2.66 | 24.52 | 9.32 | 2.34 | 26.70 | 14.60 | 6.93 |
| c | 60.40 | 33.75 | 12.23 | 60.64 | 33.83 | 12.07 | 55.30 | 31.22 | 12.16 | 55.75 | 31.46 | 11.73 | 43.75 | 27.11 | 13.65 |
| d | 5.02 | .85 | .10 | 5.02 | .85 | .08 | 5.74 | 1.39 | .17 | 5.70 | 1.11 | .18 | 9.70 | 4.08 | 1.82 |
| e | 21.89 | 7.06 | 1.06 | 21.94 | 7.18 | 1.14 | 21.27 | 7.62 | 1.34 | 21.41 | 6.76 | 1.33 | 19.55 | 8.74 | 3.52 |
| f | 54.09 | 27.43 | 7.52 | 54.23 | 28.08 | 8.04 | 49.47 | 24.37 | 7.54 | 50.07 | 25.06 | 6.98 | 34.81 | 17.61 | 7.32 |
Figure 5.
Type I error and power of likelihood-ratio tests with 500 sib trios at the nominal significance level of 0.01 under nonnormality. The curves for the estimated and true transformations are indistinguishable.
We also evaluated the estimators for the covariate effects, variance components, and heritability at the true QTL. As shown in tables 2 and 3, the estimators under the new method performed as well as did the estimators with known transformation. The estimators under the existing method without transformation were quite biased, and the estimators under the existing method with the log or square-root transformation also had bias.
Table 2.
Means and SDs of Parameter Estimators under Nonnormality, with 200 Sib Pairs
| Mean (SD) of Parameter Estimator with | ||||
|---|---|---|---|---|
| Unspecified Transformation | Known Transformation | |||
| Model | β1 | σ2_g_ | β1 | σ2_g_ |
| a | −.486 (.115) | .080 (.120) | −.499 (.111) | .081 (.121) |
| b | −.486 (.115) | .212 (.178) | −.499 (.111) | .217 (.179) |
| c | −.486 (.114) | .388 (.205) | −.499 (.110) | .398 (.205) |
| d | −.493 (.118) | .086 (.129) | −.499 (.115) | .086 (.127) |
| e | −.494 (.117) | .210 (.181) | −.499 (.114) | .211 (.176) |
| f | −.497 (.117) | .368 (.202) | −.499 (.114) | .369 (.192) |
Table 3.
Means and SDs of Estimators of h_2_g under Nonnormality, with 200 Sib Pairs
| Mean (SD) for Estimator with | |||||
|---|---|---|---|---|---|
| Specified Transformation | |||||
| Model | Unspecified Transformation | True | Square Root | Log | Identity |
| a | .043 (.063) | .041 (.061) | .047 (.070) | .046 (.068) | .080 (.132) |
| b | .113 (.093) | .109 (.090) | .110 (.097) | .109 (.097) | .126 (.150) |
| c | .207 (.104) | .200 (.101) | .193 (.112) | .193 (.110) | .184 (.162) |
| d | .044 (.065) | .043 (.064) | .046 (.069) | .046 (.067) | .064 (.108) |
| e | .107 (.088) | .106 (.088) | .103 (.091) | .103 (.090) | .103 (.125) |
| f | .184 (.093) | .185 (.094) | .175 (.099) | .176 (.098) | .149 (.133) |
To mimic the COGA data, we considered model (5) with identity H but generated the residual error for 1% of the families from the exponential distribution with mean of 4. Table 4 shows the type I error and power of the new and existing methods at the true QTL, and figure 6 displays the results for the genome scans. The new method continues to provide accurate control of type I error, whereas the type I error for the existing method is vastly inflated. The former tends to be more powerful than the latter when the genetic effects are strong. In the power comparisons, we did not reset the critical values to achieve the nominal significance levels. Such comparisons give unfair disadvantages to the new method, because the existing method has much higher type I error. Were the existing method adjusted to have correct type I error, its power would be drastically reduced.
Table 4.
Type I Error and Power (%) of Likelihood-Ratio Tests in the Presence of Outliers, with 200 Sib Trios
| Type I Error and Power (%) for | ||||||
|---|---|---|---|---|---|---|
| New Method | Existing Method | |||||
| Model | α=5 | α=1 | α=.1 | α=5 | α=1 | α=.1 |
| a | 5.16 | 1.10 | .08 | 7.95 | 2.85 | .78 |
| b | 24.12 | 8.71 | 1.73 | 25.29 | 10.86 | 3.39 |
| c | 58.84 | 32.74 | 11.65 | 54.64 | 31.22 | 13.13 |
| d | 5.29 | 1.01 | .10 | 7.62 | 2.33 | .60 |
| e | 22.37 | 7.45 | 1.32 | 23.02 | 9.51 | 2.42 |
| f | 53.00 | 27.71 | 8.37 | 49.59 | 27.32 | 10.01 |
Figure 6.
Type I error and power of likelihood-ratio tests with 500 sib trios at the nominal significance level of 0.01 with the presence of outliers.
For positive nonnormal trait data, one may consider the Box-Cox transformation
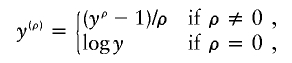
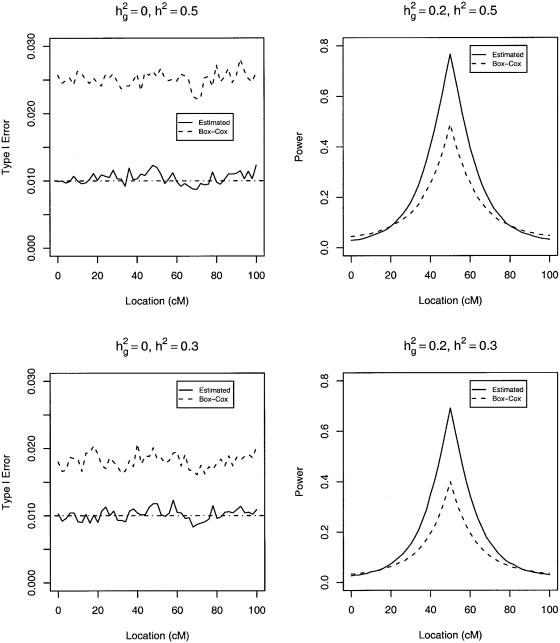
and include ρ as an unknown parameter in the parametric likelihood. If the true transformation belongs to the Box-Cox family or can be approximated by a member of the family, then this method will perform well. For example, the true transformation in our first series of simulation studies can be approximated very well by the Box-Cox transformation with ρ=0.22. In this case, the Box-Cox transformation method performance was very similar to our proposed method (results not shown). As shown in figure 7, the Box-Cox transformation causes inflated type I error and diminished power when the true transformation cannot be approximated well by a member of the Box-Cox family. The Box-Cox transformation also performed poorly in the aforementioned simulation studies with outliers (results not shown).
Figure 7.
Type I error and power of likelihood-ratio tests with 500 sib trios at the nominal significance level of 0.01 when the true transformation is H(y)=log(2_y_-2)/2.
We also compared the new method with the revised Haseman-Elston regression method (Elston et al. 2000). We generated trait values for sib pairs from the model logY _ij_=b ij+e ij. We regressed the cross product of the sib pair’s mean-centered trait values on the proportion of alleles shared IBD by the pair. The results for 500 sib pairs are shown in table 5. The new method again has proper control of type I error. The Haseman-Elston method has proper type I error at the nominal significance level of 5% but is conservative at nominal levels of 1% and 0.1%. These findings agree well with those of Allison et al. (2000). The Haseman-Elston method is substantially less powerful than the new method.
Table 5.
Type I Error and Power (%) of the New and Haseman-Elston Methods for Log-Normal Traits, with 500 Sib Pairs
| Type I Error and Power (%) for | ||||||
|---|---|---|---|---|---|---|
| New Method | Haseman-Elston Method | |||||
| Model | α=5 | α=1 | α=.1 | α=5 | α=1 | α=.1 |
| a | 5.18 | 1.02 | .10 | 4.38 | .44 | .01 |
| b | 22.45 | 7.80 | 1.42 | 9.59 | 1.51 | .05 |
| c | 53.88 | 28.05 | 9.21 | 17.84 | 3.79 | .32 |
| d | 5.01 | .92 | .02 | 4.61 | .40 | .00 |
| e | 20.16 | 6.26 | .83 | 10.21 | 1.55 | .15 |
| f | 49.23 | 22.76 | 5.71 | 19.18 | 4.41 | .50 |
Discussion
In her invited editorial, Feingold (2002) described three criteria for evaluating QTL-mapping methods: (1) the power of the method is high when the trait is normally distributed, (2) the type I error is correct regardless of the characteristics of the data, and (3) the method is still powerful when the trait is not normally distributed. The existing variance-component methods satisfy the first criterion but perform poorly on the second and third criteria, whereas the new method meets all three criteria. If one adds a fourth criterion that the method allows arbitrary pedigrees and flexible genetic models, then the new method is the only QTL-mapping method with all these desirable properties.
The new method is independent of the estimation of multipoint IBD allele–sharing probabilities. One can choose appropriate software according to the size and complexity of the pedigrees as well as the number of markers. Software such as GENEHUNTER (Kruglyak et al. 1996) and ACT (Amos 1994) performs exact multipoint calculations that are based on a hidden Markov model (Lander and Green 1987) and can handle an arbitrary number of markers for small pedigrees, whereas the approximation method implemented in SOLAR (Almasy and Blangero 1998) can handle large pedigrees.
We have implemented an efficient and reliable algorithm for the new method in a cost-free computer program (D.Y.L.'s Web site). It is more time consuming to fit the proposed semiparametric variance-components model than the existing parametric models, but the computing time is comparable and is not a concern with current computing power. It took 1 s and 6 s on an IBM BladeCenter HS-20 machine to perform the analysis at one position for the COGA data with use of the existing and new methods, respectively. For the simulations, at one position, an analysis based on the existing and new methods took 0.75 s and 1.8 s, respectively, for 200 sib trios, and 5 and 10 s, respectively, for 500 sib trios. In the simulation studies, we generated thousands of data sets and fit millions of models. Our algorithm converged in all cases.
In some studies, families are selected on the basis of the trait values of their members. If the ascertainment criterion is known, then we can divide the likelihood by the probability that the proband falls into the specified ascertainment region. An alternative approach, which does not require knowledge of the ascertainment scheme, is to condition on the actual observed trait values. de Andrade and Amos (2000) conducted simulation studies to assess the performance of these two methods in the variance-component analysis. Their results show that (1) there is little difference between the two methods of ascertainment correction, (2) failing to correct for ascertainment affects the polygenetic and environmental components of variance but has little impact on the linked major-gene component of variance, (3) regardless of whether the data are corrected for ascertainment, the power to detect a major locus is similar, and (4) there is some inflation of type I error in the presence of a large genetic background and a rare gene. Ignoring selective sampling should have less impact on the new method, since it is robust to the induced nonnormality. Further investigation is warranted.
In the COGA data, the three outliers are so extreme that it is perhaps sensible to delete them. In general, it may not be justifiable to delete outliers unless they are known to be caused by measurement or recording error. In many studies, the distinction between outliers and nonoutliers is blurred, so that it is difficult to decide which ones to delete. Another strategy is to Winsorize the data—that is, to replace the outliers with some smaller values—but this is also a highly subjective process. The results of the variance-components analysis can change dramatically dependent on how the outliers are Winsorized, which ones are deleted, or which transformation is used. The new method avoids any manipulation of data and provides unique and reliable results.
Amos (1994) and Amos et al. (1996) considered the generalized estimating-equations approach (Prentice and Zhao 1991) for estimating variance components. This method is more robust than the parametric-likelihood method under nonnormality but is less efficient than the latter. We expect our method to perform better than the generalized estimating-equations approach, since it is robust against nonnormality and outliers and has the same efficiency as the parametric-likelihood method under normality or with known transformation. It would be worthwhile to compare the two methods by simulation.
Blangero et al. (2000) proposed robust variance-covariance estimators for the parameter estimators under the normal model. They showed that the likelihood-ratio statistics can be multiplied by a constant to yield a robust test. Finding an appropriate constant is computationally intensive and requires modeling assumptions. Although it may correct type I error, this approach may not have good power. Another strategy is to obtain P values by simulation, as recommended by Allison et al. (2000). Like the use of robust variances, this approach reduces the power. There have been some other suggestions in the literature, but they are also unsatisfactory.
In some studies, the trait values are truncated because of inability to detect values below (or above) certain thresholds. One example is the coronary artery calcification (CAC) data from the Family Heart Study (Higgins et al. 1996). The distribution of CAC exhibits a spike at the left end, since a large proportion of CAC measures are recorded as 0 because they do not exceed some threshold for detection. In addition, the positive CAC scores are highly skewed. We are currently extending our idea for analysis of such data by using a mixture model that formulates the probability of a positive CAC score with a logistic-regression model and the distribution of the positive score with model (1). The resultant procedure will be more robust than the parametric Tobit variance-component method of Epstein et al. (2003).
In many longitudinal studies, such as the Framingham Heart Study (Geller et al. 2003), quantitative traits are measured repeatedly over time. In addition to the correlation among different individuals of the same family, there is within-subject correlation among the repeated measures of the same individual. de Andrade et al. (2002) extended the parametric variance-component approach to account for the within-subject correlation. We are currently exploring the extension of our approach to this setting.
Acknowledgments
This research was supported by the National Institutes of Health (NIH). The authors are grateful to the COGA investigators, for the use of their data; and to Drs. Raymond Crowe and Jean W. MacCluer, for facilitating the transfer of the COGA data from Genetic Analysis Workshop 11, which was supported in part by NIH grant GM31575.
Appendix A
Let α_k_=Λ{Y(k)}, _k_=1,…,K, where Y(k) is the k_th order statistic of Y and K is the total number of distinct trait values. Note that α_k is the jump size of Λ(y) at y_=Y(k). The system of score functions—that is, the first derivatives of the log-likelihood function (4) with respect to the parameters (β, γ, α1,…,α_K)—are given by
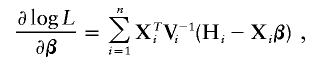
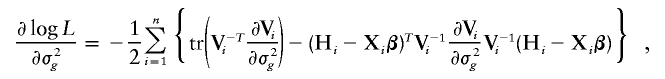
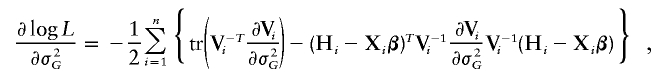
and
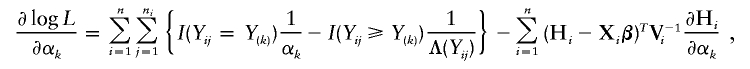
where
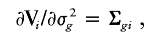

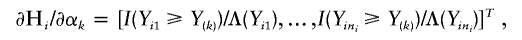
and I(𝒜) is the indicator function with a value of 1 if 𝒜 is true and of 0 otherwise. Here, γ=(σ2_g_,σ2_G_), and Σ_gi_ and Σ_Gi_ are the estimated IBD allele–sharing probability matrix at the major locus and the expected IBD allele–sharing probability matrix for the _i_th family, respectively.
By setting the system of score functions to 0, we obtain the maximum-likelihood estimators  . We then estimate Λ(y) by
. We then estimate Λ(y) by 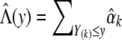 and estimate H(y) by
and estimate H(y) by 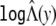 . Note that
. Note that 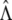 and
and 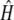 are step functions that jump at the observed trait values only. This is similar to the Breslow estimator of the cumulative hazard function and the Kaplan-Meier estimator of the survival function.
are step functions that jump at the observed trait values only. This is similar to the Breslow estimator of the cumulative hazard function and the Kaplan-Meier estimator of the survival function.
Web Resource
The URL for data presented herein is as follows:
- D.Y.L.'s Web site, http://www.bios.unc.edu/~lin (for the computer program)
References
- Allison DB, Fernández JR, Heo M, Beasley TM (2000) Testing the robustness of the new Haseman-Elston quantitative-trait loci–mapping procedure. Am J Hum Genet 67:249–252 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Allison DB, Neale MC, Zannolli R, Schork NJ, Amos CI, Blangero J (1999) Testing the robustness of the likelihood-ratio test in a variance-component quantitative-trait loci–mapping procedure. Am J Hum Genet 65:531–544 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Almasy L, Blangero J (1998) Multipoint quantitative-trait linkage analysis in general pedigrees. Am J Hum Genet 62:1198–1211 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Amos CI (1994) Robust variance-components approach for assessing genetic linkage in pedigrees. Am J Hum Genet 54:535–543 [PMC free article] [PubMed] [Google Scholar]
- Amos CI, Krushkal J, Thiel TJ, Young A, Zhu DK, Boerwinkle E, de Andrade M (1997) Comparison of model-free linkage mapping strategies for the study of a complex trait. Genet Epidemiol 14:743–748 [DOI] [PubMed] [Google Scholar]
- Amos CI, Zhu DK, Boerwinkle E (1996) Assessing genetic linkage and association with robust components of variance approaches. Ann Hum Genet 60:143–160 [DOI] [PubMed] [Google Scholar]
- Barnholtz JS, de Andrade M, Page GP, King TM, Peterson LE, Amos CI (1999) Assessing linkage of monoamine oxidase B in a genome-wide scan using a univariate variance components approach. Genet Epidemiol Suppl 1 17:S49–S54 [DOI] [PubMed] [Google Scholar]
- Begleiter H, Reich T, Hesselbrock V, Porjesz B, Li TK, Schuckit MA, Edenberg HJ, Rice JP (1995) The Collaborative Study on the Genetics of Alcoholism. Alcohol Health Res World 19:228–236 [PMC free article] [PubMed] [Google Scholar]
- Bickel PJ, Klassen CAJ, Ritov Y, Wellner JA (1993) Efficient and adaptive estimation in semiparametric models. Johns Hopkins University Press, Baltimore [Google Scholar]
- Blangero J, Williams JT, Almasy L (2000) Robust LOD scores for variance component-based linkage analysis. Genet Epidemiol Suppl 19:S8–S14 [DOI] [PubMed] [Google Scholar]
- Breslow NE (1972) Discussion of the paper by DR Cox. J R Statist Soc B 34:216–217 [Google Scholar]
- Chiou JM, Liang KY, Chiu YF (2005) Multipoint linkage mapping using sibpairs: non-parametric estimation of trait effects with quantitative covariates. Genet Epidemiol 28:58–69 10.1002/gepi.20036 [DOI] [PubMed] [Google Scholar]
- Cox DR (1972) Regression models and life-tables (with discussion). J R Statist Soc B 34:187–220 [Google Scholar]
- de Andrade M, Amos CI (2000) Ascertainment issues in variance components models. Genet Epidemiol 19:333–344 [DOI] [PubMed] [Google Scholar]
- de Andrade M, Gueguen R, Visvikis S, Sass C, Siest G, Amos CI (2002) Extension of variance components approach to incorporate temporal trends and longitudinal pedigree data analysis. Genet Epidemiol 22:221–232 10.1002/gepi.01118 [DOI] [PubMed] [Google Scholar]
- Drigalenko E (1998) How sib pairs reveal linkage. Am J Hum Genet 63:1242–1245 [PMC free article] [PubMed] [Google Scholar]
- Elston RC, Buxbaum S, Jacobs KB, Olson JM (2000) Haseman and Elston revisited. Genet Epidemiol 19:1–17 [DOI] [PubMed] [Google Scholar]
- Epstein MP, Lin X, Boehnke M (2003) A Tobit variance-component method for linkage analysis of censored trait data. Am J Hum Genet 72:611–620 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Feingold E (2001) Methods for linkage analysis of quantitative trait loci in humans. Theor Popul Biol 60:167–180 10.1006/tpbi.2001.1545 [DOI] [PubMed] [Google Scholar]
- ——— (2002) Regression-based quantitative-trait–locus mapping in the 21st century. Am J Hum Genet 71:217–222 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Forrest W (2001) Weighting improves the “new Haseman-Elston” method. Hum Hered 52:47–54 10.1159/000053353 [DOI] [PubMed] [Google Scholar]
- Fulker DW, Cherny SS, Cardon LR (1995) Multipoint interval mapping of quantitative trait loci, using sib pairs. Am J Hum Genet 56:1224–1233 [PMC free article] [PubMed] [Google Scholar]
- Geller F, Dempfle A, Gorg T (2003) Genome scan for body mass index and height in the Framingham Heart Study. BMC Genet Suppl 4:S91 10.1186/1471-2156-4-S1-S91 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Goldgar DE (1990) Multipoint analysis of human quantitative genetic variation. Am J Hum Genet 47:957–967 [PMC free article] [PubMed] [Google Scholar]
- Haseman JK, Elston RC (1972) The investigation of linkage between a quantitative trait and a marker locus. Behav Genet 2:3–19 10.1007/BF01066731 [DOI] [PubMed] [Google Scholar]
- Higgins M, Province M, Heiss G, Eckfeldt J, Ellison RC, Folsom AR, Rao DC, Sprafka M, Williams R (1996) NHLBI Family Heart Study: objectives and design. Am J Epidemiol 143:1219–1228 [DOI] [PubMed] [Google Scholar]
- Kruglyak L, Daly M, Reeve-Daly M, Lander ES (1996) Parametric and nonparametric linkage analysis: a unified multipoint approach. Am J Hum Genet 58:1347–1363 [PMC free article] [PubMed] [Google Scholar]
- Lander ES, Green P (1987) Construction of multilocus genetic linkage maps in humans. Proc Natl Acad Sci USA 84:2363–2367 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lin DY (2004) Haplotype-based association analysis in cohort studies of unrelated individuals. Genet Epidemiol 26:255–264 10.1002/gepi.10317 [DOI] [PubMed] [Google Scholar]
- Major LF, Murphy DL (1978) Platelet and plasma amine oxidase activity in alcoholic individuals. Br J Psychiatry 132:548–554 [DOI] [PubMed] [Google Scholar]
- Pratt SC, Daly MJ, Kruglyak L (2000) Exact multipoint quantitative-trait linkage analysis in pedigrees by variance components. Am J Hum Genet 66:1153–1157 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Prentice RL, Zhao LP (1991) Estimating equations for parameters in means and covariances of multivariate discrete and continuous responses. Biometrics 47:825–839 [PubMed] [Google Scholar]
- Press WH, Teukolsky SA, Vetterling WT, Flannery BP (1992) Numerical recipes in C: the art of scientific computing, 2nd ed. Cambridge University Press, New York [Google Scholar]
- Putter H, Sandkuijl LA, van Houwelingen JC (2002) Score test for detecting linkage to quantitative traits. Genet Epidemiol 22:345–355 10.1002/gepi.01104 [DOI] [PubMed] [Google Scholar]
- Schork NJ (1993) Extended multipoint identity-by-descent analysis of human quantitative traits: efficiency, power, and modeling considerations. Am J Hum Genet 53:1306–1319 [PMC free article] [PubMed] [Google Scholar]
- Self SG, Liang KL (1987) Asymptotic properties of maximum likelihood estimators and likelihood ratio tests under nonstandard conditions. J Am Statist Assoc 82:605–610 [Google Scholar]
- Sham PC, Purcell S (2001) Equivalence between Haseman-Elston and variance-components linkage analyses for sib pairs. Am J Hum Genet 68:1527–1532 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sham PC, Purcell S, Cherny SS, Abecasis GR (2002) Powerful regression-based quantitative-trait linkage analysis of general pedigrees. Am J Hum Genet 71:238–253 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Strug L, Sun L, Corey M (2003) The genetics of cross-sectional and longitudinal body mass index. BMC Genet Suppl 4:S14 10.1186/1471-2156-4-S1-S14 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sullivan JL, Cavenar JO Jr, Maltbie AA, Lister P, Zung WW (1979) Familial biochemical and clinical correlates of alcoholics with low platelet monoamine oxidase activity. Biol Psychiatry 14:385–394 [PubMed] [Google Scholar]
- Tang H-K, Siegmund D (2001) Mapping quantitative trait loci in oligogenic models. Biostatistics 2:147–162 10.1093/biostatistics/2.2.147 [DOI] [PubMed] [Google Scholar]
- Visscher PM, Hopper JL (2001) Power of regression and maximum likelihood methods to map QTL from sib-pair and DZ twin data. Ann Hum Genet 65:583–601 10.1046/j.1469-1809.2001.6560583.x [DOI] [PubMed] [Google Scholar]
- Wang K, Huang J (2002) A score-statistic approach for the mapping of quantitative-trait loci with sibships of arbitrary size. Am J Hum Genet 70:412–424 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Williams JT, Duggirala R, Blangero J (1997) Statistical properties of a variance-components method for quantitative trait linkage analysis in nuclear families and extended pedigrees. Genet Epidemiol 14:1065–1070 [DOI] [PubMed] [Google Scholar]
- Wright FA (1997) The phenotypic difference discards sib-pair QTL linkage information. Am J Hum Genet 60:740–742 [PMC free article] [PubMed] [Google Scholar]
- Xu X, Weiss S, Xu X, Wei LJ (2000) A unified Haseman-Elston method for testing linkage with quantitative traits. Am J Hum Genet 67:1025–1028 [DOI] [PMC free article] [PubMed] [Google Scholar]