Hemagglutinin sequence clusters and the antigenic evolution of influenza A virus (original) (raw)
Abstract
Continual mutations to the hemagglutinin (HA) gene of influenza A virus generate novel antigenic strains that cause annual epidemics. Using a database of 560 viral RNA sequences, we study the structure and tempo of HA evolution over the past two decades. We detect a critical length scale, in amino acid space, at which HA sequences aggregate into clusters, or swarms. We investigate the spatio-temporal distribution of viral swarms and compare it to the time series of the influenza vaccines recommended by the World Health Organization. We introduce a method for predicting future dominant HA amino acid sequences and discuss its potential relevance to vaccine choice. We also investigate the relationship between cluster structure and the primary antibody-combining regions of the HA protein.
Keywords: quasi species‖vaccination‖clustering‖H3N2
Influenza A virus is a negative-stranded RNA virus that causes significant human mortality and morbidity worldwide (1). The virus is divided into subtypes based on major differences in the surface proteins hemagglutinin (HA) and neuraminidase, which are the most important targets for the human immune system. Within each subtype of the influenza virus, gradual mutations to the HA gene continually produce immunologically distinct strains (referred to as drift variants); an influenza infection brings lasting immunity to the infecting strain, but most people are susceptible to re-infection by a new drift variant within a few years. Over the past century, the annual epidemics associated with antigenic drift have had an even greater cumulative impact than the three pandemics associated with major reassortment events, known as antigenic shifts (2–4). Antigenic drift requires that vaccines be updated annually to correspond with the dominant epidemic strains of HA. Thus the prediction of HA's evolutionary course is of great practical importance to public health.
Recent developments in molecular biology and computation have made possible remarkable phylogenetic reconstructions of HA evolution (3, 5). Such studies reveal that modifications to HA1, the immunogenic part of HA, accrue at a dramatic rate. Those sites of HA1 involved in antigen determination exhibit significantly more non-synonymous nucleotide substitutions than synonymous substitutions (6, 7), whereas the remaining sites show the more common pattern of primarily synonymous variation. These observations demonstrate that HA is undergoing positive Darwinian selection for new antigenic variants (8). Bush et al. (9) have identified 18 HA1 codon sites with significantly higher non-synonymous to synonymous ratios. Viewed retrospectively, these 18 sites usually predict where the trunk of the phylogeny will emerge: among the circulating sequences in a given influenza season, the one with the largest number of amino acid replacements among these 18 sites is usually most closely related to future evolutionary lineages.
In this paper, we present an approach to analyzing and, to some extent, predicting the course of influenza sequence evolution. Our approach is related and complementary to phylogenetic techniques, but we are less concerned with reconstructing the evolutionary relationships between HA1 sequences. Instead, we identify natural scales at which HA1 amino acid sequences aggregate into clusters, or “swarms,” and we study their spatio-temporal patterns. We will focus on the relationships between observed cluster structure, worldwide vaccination history, and the primary antibody-combining regions of the HA protein.
Data and Methods
Data.
This study uses 560 sequences, each 987 nucleotides long, of the H3 type HA1 gene isolated between 1968 and 2000 from locations around the globe. The sequences were obtained from a public database [ref. 10; Los Alamos National Laboratory, Influenza Sequence Database (http://www.flu.lanl.gov/)]. We use the terms genotype and strain interchangeably to refer to a nucleotide sequence of HA1. Viruses were isolated by either egg or kidney cell cultures (3). All sequences were easily aligned without gaps.
Each of the 560 sequences is associated with a calendar year of isolation, in some cases inferred from the strain name. For 439 of the sequences, however, more detailed information is available, allowing them to be partitioned into influenza seasons, defined as 1 October through 30 September. For example, the “94/5 season” refers to those sequences collected between 1 October 1994 and 30 September 1995.
Most of the sequences were generated as part of the long-term World Health Organization (WHO) influenza surveillance program. As we discuss below, only a small proportion of viruses isolated by the WHO are also sequenced. Novel antigenic isolates are preferentially sequenced by the WHO (11); as a result, the database provides a biased approximation of worldwide strain frequencies.
Methods.
To identify clusters of viral sequences, we must first assign a distance between sequences. We define the distance between two HA1 sequences as the sum of the pairwise distances between their 329 composite amino acids. Several amino acid metrics are possible. The simplest metric, called the Hamming metric, equals zero or one depending on whether two amino acids are identical. Alternative metrics weight the differences between amino acids according to their stereochemical properties [e.g., the Miyata metric (12)], or their substitution frequencies in protein families (13). Here, we present results based on the Hamming metric. Results based on the Miyata metric are similar.
Ideally, the distance between a pair of sequences should reflect the immunogenic properties of the corresponding viral proteins. Some steps have been taken in this direction. For example, Lapedes and Farber (14) derived a distance measure for HA from antibody binding assays, whereas Wilson and Cox (15) developed a metric based on changes in the solvent-accessible surface of the folded HA molecule. Nonetheless, more detailed antibody-binding data and a better understanding of HA folding are required before these metrics can be comprehensively applied in our context.
Using their pairwise distances we identify a natural partitioning of the sequences into disjoint groups, or clusters, via a single-linkage clustering algorithm (16). Traditional single-linkage clustering produces a hierarchy of partitions starting with each sequence in its own unique “cluster” and successively merging clusters whose nearest neighbors are a minimal distance apart, eventually grouping all sequences into one large cluster. Cluster hierarchies have been used to generate phylogenetic trees (17). In this paper, however, we do not consider the hierarchy of clusters, but rather inspect the clusters themselves at a suitably chosen linkage distance. In this sense our analysis is a logical complement to the phylogenetic approach.
Results
Identifying Natural Scales of Aggregation.
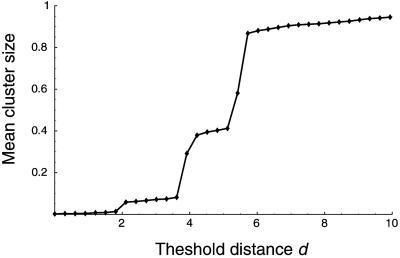
To choose a suitable threshold distance d at which to stop the single-linkage algorithm, we inspect the “cluster-size curve” (18) for all 560 sequences in the data set (Fig. 1). When d = 0, there are 468 separate clusters, indicating the number of unique amino acid sequences in the data set. When d = 18, all 560 sequences fall into a single cluster. Furthermore, Fig. 1 shows that there is a natural, nonrandom partitioning of the sequences into disjoint clusters at a threshold distance of d = 2 amino acid changes. In other words, d = 2 provides the finest natural scale at which the sequences aggregate. (There is another nonrandom partition corresponding to d = 4, at which most sequences fall into three large clusters.) The strain name and corresponding cluster for each of the 560 sequences are provided in supporting information, which is published on the PNAS web site (www.pnas.org).
Figure 1.
The cluster-size curve for 560 sequences of HA1. This curve shows the relationship between the threshold distance d (at which to connect two sequences into the same cluster) and the mean cluster size C(d), defined as the normalized first moment of the resulting distribution of cluster sizes. Equivalently, C(d) is the probability that two randomly chosen sequences lie in the same cluster. Plateaus in the cluster size curve correspond to stable length scales at which the sequences form nonrandom clusters. Random data would not exhibit any plateaus except for C = 0 and C = 1 (18). The smooth cluster size curve results from averaging over 100 probabilistic Gaussian draws for each mean distance parameter d, with a 5% coefficient of variation (18). The HA1 data exhibit two significant plateaus corresponding to clusterings at d = 2–3 and d = 4–5. The long tail for d ≥ 6 corresponds to the gradual accumulation of outlier sequences. When d = 2, there are 174 resulting clusters with C (2) = 0.0614; at this scale, the expected size of the cluster containing a randomly chosen sequence is 560 × 0.0614 = 34.4 sequences. (The clustering for d = 3 is extremely similar to d = 2, as the first plateau indicates.)
The existence of a natural scale of non-random aggregation suggests that HA1 sequences form viral swarms. There are 174 clusters corresponding to d = 2, but 134 of these clusters consist of a single outlier sequence. The abundance of outliers is probably attributable to the WHO bias toward sequencing antigenically novel strains. By focusing on the larger clusters, we filter out these outliers.
Here we use “swarm” to denote a cluster of related viral genotypes that to some degree operate as a selective unit (19–21). Viral swarms, which are shaped by mutation and selection, are often called quasispecies (22), although this usage differs from Eigen's original usage to describe a collection of macromolecules generated by mutations from a fixed wild-type configuration (23).
Spatio-Temporal Evolution of Sequence Clusters.
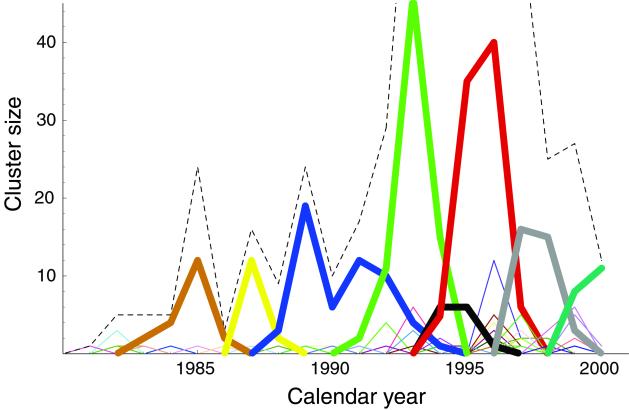
The above method for decomposing HA1 sequences into natural clusters provides a revealing perspective on the evolution of influenza virus. In Fig. 2 we plot the number of sequences in each cluster as a function of isolation year. Even though we did not use any information about isolation year when clustering the data, Fig. 2 shows that the resulting viral clusters are localized in time. There is no cluster that has members spanning more than seven collection years. Instead, dominant clusters of viral sequences tend to replace one another every 2–5 years, in agreement with the timescale of dominant antigenic replacements (24). Some clusters are significantly more long-lived than others, suggesting that HA swarms do not evolve at a constant rate.
Figure 2.
The number of HA1 sequences within each cluster plotted as a function of calendar year of isolation. The clustering shown here corresponds to d = 2 amino acids (see Fig. 1). Each cluster is indicated by a different color, with the eight largest clusters shown in bold. The dashed line indicates the total number of isolates in the data set each year. The dominant sequence clusters tend to replace each other every 2–5 years. The dominant cluster in each year accounts for more than 25% of the sequences isolated that year. (The number of sequences each year does not reflect the severity of infections, but rather the temporal biases in the sequence data set.)
Note that the swarm evolution seen in Fig. 2 is not periodic within the time-span of two decades. Once HA evolves away from a given region of sequence space, it does not later revisit that region. This result, seen here in terms of cluster structure, is consistent with the one-trunk phylogenetic reconstructions of HA1 (3). Such behavior is in sharp contrast to viruses with distinct co-circulating serotypes [e.g., avian influenza (2)], or with distinct serotypes that may cycle in time.
Host-mediated mutations acquired during viral culturing could potentially affect the structure of sequence clusters. However we believe this to be a secondary effect and find no signature of it, e.g., no cluster that spans all collection years, in the time series in Fig. 2.
It is generally believed that novel influenza A subtypes (e.g., the subtype H3N2) usually originate in Asia, especially in China. Common wisdom also holds that novel strains within each subtype (i.e., drift variants) also originate in China (3). We can use the three largest sequence clusters in Fig. 3 (those spanning seasons 87/8–93/4, 91/2–93/4, and 93/4–97/8) to test this hypothesis. We find that among the sequences within each of these large clusters, those sequences isolated in China or Hong Kong are found preferentially in the first half of the cluster's lifetime (_χ_2 = 13.0, 9.0, 8.26; P < 0.005 for all). These results support the hypothesis that dominant viral swarms tend to originate in Asia and thereafter spread across the globe.
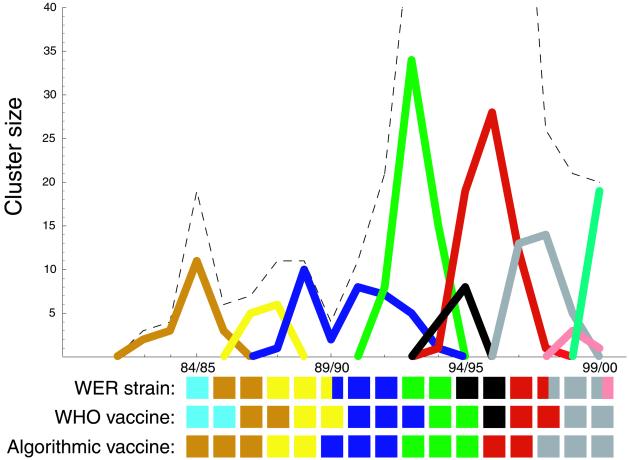
Figure 3.
The number of HA1 sequences within each cluster plotted as a function of influenza season. The graph shows the eight largest clusters as well as any other clusters that contain sequences used in a WHO vaccine. The tiles denoted “WHO vaccine” indicate the ‘color’ of the WHO-recommended vaccine in each season, e.g., the color of the cluster corresponding to the strain on which each vaccine was based. The tiles denoted “Algorithmic vaccine” indicate the color of vaccine prescribed each season by the algorithm proposed in the main text (the dominant cluster from the previous season). The tiles denoted “WER strain” indicate the color of the dominant antigenic type, based on HI assays, as reported by the WHO in its Weekly Epidemiological Record (40–56). (Note that one of the three strains reported in WER for 1999–2000 is missing from the Los Alamos sequence database.) Both vaccines tend to match the WER strains well; in some seasons the WHO vaccine matches better, and in some seasons the algorithmic vaccine matches better.
Cluster Structure and Vaccination Choice.
Each February, the World Health Organization recommends two strains of influenza A virus (one of the H1N1 subtype, and one H3N2) and one strain of influenza B virus to be used as the basis for the trivalent vaccine in the northern hemisphere influenza season (25). Choices are based on the antigenic properties of circulating strains and the immunogenic properties of vaccine candidates. The lead time is necessary for vaccine preparation. Case studies indicate that in general vaccination is extremely effective (up to 68%) for prevention (26) and for reduction of morbidity, even among unvaccinated individuals in close contact with vaccinees (27). Nevertheless, the antigenic plasticity of HA complicates the precise prediction of future dominant strains and vaccine choice (24).
Ideally, the strain used as the basis for a vaccine each season should correspond to the dominant antigenic strain that season. Unfortunately, the standard hemagglutination inhibition (HI) assay (28) offers relatively poor resolution for comparing antigenic properties of circulating strains; HI often characterizes up to 95% of strains as identical (29). More refined antigenic assays are possible, but more time consuming. Fortunately, the amino acid sequence can be more sensitive (30) and is generally correlated (29) with the results of refined HI assays.
The decomposition of HA1 sequences into disjoint clusters affords a retrospective and predictive tool for analyzing influenza vaccine choices. Fig. 3 shows the sizes of the primary HA1 clusters, each in a different color, as a function of influenza season. Fig. 3 also shows the “color” of the WHO-recommended vaccine in each season, that is, the color of the cluster corresponding to the strain on which each vaccine was based. Insofar as the color of a vaccine indicates its antigenic properties—which, we have argued, is a good first approximation—Fig. 3 provides a wealth of information about worldwide vaccination strategy. Fig. 4 lists some representative strain names that are members of the clusters in Fig. 3.
Figure 4.
Strain names of representative members from each of the clusters seen in Fig. 3. Note that strains considered as antigenically distinct by the WHO (using HI assay) can fall in the same cluster.
According to Fig. 3, a dominant cluster of influenza virus can go extinct even while the recommended vaccine is chosen from outside of the cluster (e.g., the blue cluster, 94/5). In other words, large viral swarms seem to drive themselves to extinction, presumably by stimulating immunity in the human population, even without the pressure of vaccination. This behavior corroborates the common wisdom that, although WHO's vaccination recommendations have greatly reduced human mortality, vaccination has not significantly altered the evolutionary course of HA (3). This conclusion is consistent with the constancy of HA's rate of evolution before and after the advent of widespread vaccination (2, 31).
We emphasize that the HA1 sequences used in Fig. 3 were not available at the time when the WHO recommended the indicated vaccines. Only recently has it become possible to sequence an isolate's HA1 gene within the same season of the virus's isolation. This technological advance in sequencing speed may allow HA1 sequences to play an expanded role, complementing HI assays, in informing vaccine selection.
With these provisos in mind, we now consider a sequence-based algorithm for choosing vaccine strains. Given the limited amount of available data, we examine the simplest of such algorithms. First, we cluster all of the sequences collected during or before the current influenza season (using d = 2 amino acid changes). Then, we choose the HA sequence on which to base next season's vaccine as the most recent sequence in the current season's most dominant cluster. Fig. 3 shows the vaccines that would have been specified by this algorithm. The algorithm would have agreed with the actual choices made by the WHO in nine of the last 16 flu seasons, and it would have specified different choices in seven seasons.
Our interpretation of Fig. 3 depends on the assumption that the sequence database reflects worldwide strain frequencies each season. But our database is limited and potentially biased; only a small proportion of viruses characterized by HI assays are actually sequenced. By choosing the appropriate scale of aggregation (Fig. 1), we have tried to mitigate the influence of outlier sequences. Nevertheless, the bias toward novelty in the sequence database may cause sequence clusters to peak before the corresponding actual antigenic types do. (Conversely, the coarseness of the HI assay and the need to group types in real time may cause the Weekly Epidemiological Record identification to lag slightly behind actual antigenic changes.)
We emphasize that Fig. 3 provides only an approximate indication of vaccine suitability. Vaccines should ideally match the dominant antigenic properties of circulating influenza sequences each season. The extent of the vaccine's correlation with the dominant amino acid sequence of influenza strains, indicated by the colors in Fig. 3, is related but not identical to antigenic correlation. The Hamming metric on sequences has been used as an effective model of antigenic distances for B-cells in general (32) and for influenza in particular (33). Nevertheless, comparison of sequence data to direct immunological assays should be used to quantify the correlation between amino acid composition and antigenic properties (14). The algorithm above cannot be considered for use as a vaccine protocol until direct antigenic data are incorporated. Our methodology for evaluating vaccine candidates would be relatively easy to generalize using a combination HI- and sequence-derived metric.
Cluster Structure and Antibody-Combining Sites.
The underlying mechanism of influenza A's antigenic plasticity, that is, how the virus continually evades immunity by producing variant strains, remains an outstanding evolutionary problem with obvious practical implications. To address this question, we inspect the structure of the identified sequence clusters with regards to the known epitopes (antibody-combining regions) of HA.
Of the 329 codon sites in the HA1 gene, 131 sites lie in or near the five main epitopes of the HA trimer, labeled A through E (15). Epitopic sites have been shown to exhibit greater variability, higher ratios of replacement to silent mutations, and greater correlation with future phylogenetic trajectory (9)—the hallmarks of divergent selection. Having partitioned the HA sequences into clusters we may now ask specifically: (i) whether different clusters are unusually homogenous with respect to different epitopes, and (ii) whether different epitopes change each time influenza “jumps” from one cluster to the next.
For each of the epitopes, Fig. 5 shows the within-cluster variation and the size of the “jumps” between the eight largest clusters in our data set. We see some intriguing interactions between epitopes and viral swarms: four of the five epitopes account for the greatest amount of variation in at least one cluster. Many of the epitopes also show interesting temporal patterns. For example, the within-cluster variation in epitope B declines sharply from the early clusters to the late clusters; the within-cluster variation of epitope D is prominent in the middle clusters and then later declines.
Figure 5.
Within-cluster variation (a) and between-cluster distances (b), by epitope, for the eight largest clusters in our data set. Within-cluster variation is calculated as the mean pairwise Hamming distance, restricted to sites in a given epitope, among sequences in a cluster. The abscissa shows the mean of the calendar years for each cluster's sequences. Note that the amount of variation among the 198 nonepitopic sites is of roughly the same magnitude as variation in each of the epitopes. In b, the distance between successive clusters is calculated as the distance between the cluster centroids in Hamming space (using the Manhattan metric). The abscissa shows the temporal midpoint of the two clusters being compared. Note that the epitope with the largest inter-cluster change is never repeated in two successive “jumps.”
Even more striking is the pattern of epitope changes when jumping from one cluster to the next. Each jump is dominated by a different epitope than the previous jump. For example, the difference between the 1985 and 1987 clusters is greatest along epitope B, whereas the difference from 1987 to 1990 is greatest along epitope A. This suggests that influenza must jump in a different direction, i.e., along a different epitopic axis, every 2–5 years to escape from the immune system. The pattern of inter-cluster jumps quantifies and verifies the criteria of Wilson and Cox (15) that new drift variants require more than four amino acid changes across two or more antigenic sites.
Moreover, the “non-epitopic” sites of HA1 show increasing intra-cluster variability (Fig. 5a) and dramatically larger jumps between clusters (Fig. 5b) in recent years. These trends suggest that the locations of epitopic sites on the HA trimer may have evolved since their original characterization (9, 15).
Furthermore, we find a strong correlation between within-cluster variation and jump distance; in five cases the epitope of largest within-cluster variation jumps the furthest (and in the other two cases the epitope of second largest variation jumps the furthest). In other words, large evolutionary changes in an epitope are possible only when a cluster features sufficient variation on which selection may act.
We suspect that substantially more data, including antibody-binding or protein-folding information, will be needed to tease apart all of the patterns in Fig. 5. We also need a clearer understanding of how immune reactions shape swarm structure and epitopic sequence variation. In particular, what does convergence or divergence of a particular epitope in a cluster imply about immuno-dominance? For example, does the small amount of within-cluster variation seen in epitope A in the 1985 cluster indicate that this epitope is a prime immune target for strains in that cluster, and is thus unable to vary from a fixed adaptive sequence; or does it indicate that epitope A is under less immune pressure than other epitopes, and thus does not need to vary?
Discussion
The study of viral sequence evolution, and influenza virus evolution in particular, has traditionally relied on phylogenetic techniques. Here we have presented formal cluster-based techniques that can complement traditional methodologies by detecting natural scales of sequence aggregation. The resulting partition of viral sequences into clusters yields new perspectives on the structure of their genomic evolution.
Although phylogenetic algorithms can estimate the evolutionary relationships among sequences, influenza phylogenies, even those using extensive databases, are often plagued by poor bootstrap values and instabilities of tree topology, which have been systematically studied by only a few authors (3, 11, 34). The problem of resolving an evolutionary time series to the level of individual sequences is thus difficult, but perhaps unnecessary. Considerable evidence (20–22), suggests that rapidly evolving RNA viruses effectively experience selection as swarms, rather than as individuals. The techniques developed here allow us to inspect viral evolution at the scale at which selection acts.
In this paper we have demonstrated that HA1 sequences cluster in a non-random fashion, that clusters replace one another every 2–5 years, that the persistence of clusters can be used to predict the next season's influenza sequences, and that clusters demonstrate interesting interactions with the five main antibody-combining regions of hemagglutinin. All of these results rely intrinsically upon the quasispecies [see Domingo _et al._ (22)] nature of the influenza A virus.
Recently, there has been increasing theoretical interest in the ecology and evolution of influenza and other diseases with antigenically distinct, interacting strains (35–39). Our results provide empirical grounding for that work, and identify the viral swarm as a “fundamental particle” for modeling. The dynamics of influenza A viral evolution thus will be driven by selection pressures upon swarms, as mediated by patterns of cross-reactivity among them.
Although the approaches developed here offer an important complement to phylogenetic techniques, our results perhaps raise as many questions as they answer. Our method of predicting future dominant influenza sequences still requires antibody-binding assays before use as a vaccine protocol. Similarly, the observed cluster-epitope interactions may indicate important directions for influenza modeling, but their immunological interpretation is not yet clear. Despite these remaining questions, our results emphasize the importance of an integrated approach to the ecology and evolution of influenza virus. A focus on the cluster as the core element of influenza A dynamics not only provides a framework for understanding the evolutionary history of the virus; it also helps to inform the prediction of future outbreaks.
Supplementary Material
Supporting Table
Acknowledgments
We are grateful for valuable discussions with Viggo Andreasen, Freddy Christiansen, David Earn, Juan Lin, Ellis McKenzie, Alan Perelson, Tom Reichert, Derek Smith, Lone Simonsen, and Martin Weigert. We especially thank Walter Fitch, Peter Palese, Robin Bush, and Nancy Cox for critical readings of the manuscript, but we do not imply that they necessarily endorse our interpretation of the results. We thank Los Alamos National Laboratories and all who have contributed to the Influenza Sequence Database, including those who have contributed unpublished sequences: N. Komadina, A. Hapson, N. Cox, C. Bender, O. Hungnes, and M. Brytting. This work was supported by a grant from the National Institutes of Health, no. 1-R01-GM60729-01 to S.A.L. We also thank the Alfred P. Sloan Foundation, The Ambrose Monell Foundation, The Florence Gould Foundation, and the J. Seward Johnson Trust. J.B.P. acknowledges support from the National Science Foundation, the Teresa and H. John Heinz III Foundation, and the Burroughs Wellcome Fund.
Abbreviations
HA
hemagglutinin
WHO
World Health Organization
HI
hemagglutination inhibition
References
- 1.Hayden F G, Palese P. In: Clinical Virology. Richman D, Whitley R J, Hayden F G, editors. New York: Churchill Livingstone; 1997. pp. 911–942. [Google Scholar]
- 2.Webster R G, Bean W J, Gorman O T, Chambers T M, Kawaoka Y. Microbiol Rev. 1992;56:152–179. doi: 10.1128/mr.56.1.152-179.1992. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Fitch W M, Bush R M, Bender C A, Cox N J. Proc Natl Acad Sci USA. 1997;94:7712–7718. doi: 10.1073/pnas.94.15.7712. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Webster R G. Emerg Infect Dis. 1998;4:436–441. doi: 10.3201/eid0403.980325. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Fitch W M, Bush R M, Bender C A, Subbarao K, Cox N J. J Hered. 2000;91:183–185. doi: 10.1093/jhered/91.3.183. [DOI] [PubMed] [Google Scholar]
- 6.Ina Y, Gojobori T. Proc Natl Acad Sci USA. 1994;91:8388–8392. doi: 10.1073/pnas.91.18.8388. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Bush R M, Fitch W M, Bender C A, Cox N J. Mol Biol Evol. 1999;16:1457–1465. doi: 10.1093/oxfordjournals.molbev.a026057. [DOI] [PubMed] [Google Scholar]
- 8.Fitch W, Leiter J, Li X, Palese P. Proc Natl Acad Sci USA. 1991;88:4270–4274. doi: 10.1073/pnas.88.10.4270. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Bush R M, Bender C A, Subbarao K, Cox N J, Fitch W M. Science. 1999;286:1921–1925. doi: 10.1126/science.286.5446.1921. [DOI] [PubMed] [Google Scholar]
- 10.Macken C, Lu H, Goodman J, Boykin L. In: Options for the Control of Influenza IV. Osterhaus A D M E, editor. Amsterdam: Elsevier; 2002. , in press. [Google Scholar]
- 11.Bush R M, Smith C B, Cox N J, Fitch W M. Proc Natl Acad Sci USA. 2000;97:6974–6980. doi: 10.1073/pnas.97.13.6974. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Miyata T, Miyazawa S, Yashunaga T. J Mol Evol. 1979;12:219–236. doi: 10.1007/BF01732340. [DOI] [PubMed] [Google Scholar]
- 13.Henikoff S, Henikoff J G. Proc Natl Acad Sci USA. 1992;89:10915–10919. doi: 10.1073/pnas.89.22.10915. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Lapedes A, Farber R. J Theor Biol. 2001;212:57–69. doi: 10.1006/jtbi.2001.2347. [DOI] [PubMed] [Google Scholar]
- 15.Wilson I A, Cox N J. Annu Rev Immunol. 1990;8:737. doi: 10.1146/annurev.iy.08.040190.003513. [DOI] [PubMed] [Google Scholar]
- 16.Duda R, Hart P, Stork D. Pattern Classification. New York: Wiley; 1998. [Google Scholar]
- 17.Saitou N, Nei M. Jpn J Genet. 1986;61:611. [Google Scholar]
- 19.Domingo E, Holland J J. Annu Rev Microbiol. 1997;51:151–178. doi: 10.1146/annurev.micro.51.1.151. [DOI] [PubMed] [Google Scholar]
- 20.Domingo E, Mededez-Arias L, Quinones-Mateu M, Holguin A, Gutierrez-Rivas M, Martinez M, Quer J, Novella I, Holland J. Prog Drug Res. 1997;48:99–128. doi: 10.1007/978-3-0348-8861-5_4. [DOI] [PubMed] [Google Scholar]
- 21.Nowak M A, May R M. Virus Dynamics: The Mathematical Foundations of Immunology and Virology. Oxford: Oxford Univ. Press; 2000. [Google Scholar]
- 22.Domingo E, Holland J J, Biebricher C K. Quasispecies and RNA Virus Evolution: Principles and Consequences. Austin, TX: Landes; 2002. [Google Scholar]
- 23.Eigen M. Naturwissenschaften. 1971;58:465–523. doi: 10.1007/BF00623322. [DOI] [PubMed] [Google Scholar]
- 24.Cox N J, Bender C A. Semin Virol. 1995;6:359–370. [Google Scholar]
- 25.World Health Organization. Weekly Epidem Rec. 2001;76:58–61. [Google Scholar]
- 26.Demicheli V, Jefferson T, Rivetti D, Deeks J. Vaccine. 2000;18:957–1030. doi: 10.1016/s0264-410x(99)00332-1. [DOI] [PubMed] [Google Scholar]
- 27.Hurwitz E, Haber M, Chang A, Shope T, Teo S, Ginsberg M, Waecker N, Cox N. J Am Med Assoc. 2000;284:1677–1682. doi: 10.1001/jama.284.13.1677. [DOI] [PubMed] [Google Scholar]
- 28.Chakraverty P. Bull World Health Org. 1971;45:755–766. [PMC free article] [PubMed] [Google Scholar]
- 29.Ellis J S, Chakraverty P, Clewley J P. Arch Virol. 1995;140:1889–1904. doi: 10.1007/BF01322680. [DOI] [PubMed] [Google Scholar]
- 30.Hay A, Gregory V, Douglas A, Lin Y. Philos Trans R Soc London B. 2001;356:1861–1870. doi: 10.1098/rstb.2001.0999. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Gibbs M J, Armstrong J S, Gibbs A J. Science. 2001;293:1842–1845. doi: 10.1126/science.1061662. [DOI] [PubMed] [Google Scholar]
- 32.Kohler V, Puzone R, Seiden P E, Celada F. Vaccine. 2000;19:862–876. doi: 10.1016/s0264-410x(00)00225-5. [DOI] [PubMed] [Google Scholar]
- 33.Smith D J, Forrest S, Ackley D H, Perelson A S. Proc Natl Acad Sci USA. 1999;96:14001–14006. doi: 10.1073/pnas.96.24.14001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Bush R M. Nat Rev Genet. 2001;2:387–392. doi: 10.1038/35072023. [DOI] [PubMed] [Google Scholar]
- 35.Castillo-Chavez C, Hethcote H W, Andreasen V, Levin S A, Liu W M. J Math Biol. 1989;27:233–258. doi: 10.1007/BF00275810. [DOI] [PubMed] [Google Scholar]
- 36.Gupta S, Maiden M C J, Feavers I M, Nee S, May R M, Anderson R M. Nat Med. 1996;2:437–442. doi: 10.1038/nm0496-437. [DOI] [PubMed] [Google Scholar]
- 37.Andreasen V, Lin J, Levin S A. J Mol Biol. 1997;35:825–842. doi: 10.1007/s002850050079. [DOI] [PubMed] [Google Scholar]
- 38.Gupta S, Ferguson N, Anderson R. Science. 1998;280:912–915. doi: 10.1126/science.280.5365.912. [DOI] [PubMed] [Google Scholar]
- 39.Lin J, Andreasen V, Levin S A. Math Biosci. 1999;162:33–51. doi: 10.1016/s0025-5564(99)00042-5. [DOI] [PubMed] [Google Scholar]
- 40.World Health Organization. Wkly Epidemiol Rec. 1984;59:55. [Google Scholar]
- 41.World Health Organization. Wkly Epidemiol Rec. 1985;60:53. [Google Scholar]
- 42.World Health Organization. Wkly Epidemiol Rec. 1986;61:61. [Google Scholar]
- 43.World Health Organization. Wkly Epidemiol Rec. 1987;62:54. [Google Scholar]
- 44.World Health Organization. Wkly Epidemiol Rec. 1988;63:58. [Google Scholar]
- 45.World Health Organization. Wkly Epidemiol Rec. 1989;64:54. , 302. [Google Scholar]
- 46.World Health Organization. Wkly Epidemiol Rec. 1990;65:53. , 303. [Google Scholar]
- 47.World Health Organization. Wkly Epidemiol Rec. 1991;66:57. , 311. [Google Scholar]
- 48.World Health Organization. Wkly Epidemiol Rec. 1992;67:57. , 291. [Google Scholar]
- 49.World Health Organization. Wkly Epidemiol Rec. 1993;68:288. [Google Scholar]
- 50.World Health Organization. Wkly Epidemiol Rec. 1994;69:291. [Google Scholar]
- 51.World Health Organization. Wkly Epidemiol Rec. 1995;70:53. , 277. [Google Scholar]
- 52.World Health Organization. Wkly Epidemiol Rec. 1996;71:57. , 289. [Google Scholar]
- 53.World Health Organization. Wkly Epidemiol Rec. 1997;72:57. , 293. [Google Scholar]
- 54.World Health Organization. Wkly Epidemiol Rec. 1998;73:56. , 305. [Google Scholar]
- 55.World Health Organization. Wkly Epidemiol Rec. 1999;74:57. , 321. [Google Scholar]
- 56.World Health Organization. Wkly Epidemiol Rec. 2000;75:61. , 329. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Supporting Table