Evaluating conformational free energies: The colony energy and its application to the problem of loop prediction (original) (raw)
Abstract
In this paper, we introduce a method to account for the shape of the potential energy curve in the evaluation of conformational free energies. The method is based on a procedure that generates a set of conformations, each with its own force-field energy, but adds a term to this energy that favors conformations that are close in structure (have a low rmsd) to other conformations. The sum of the force-field energy and rmsd-dependent term is defined here as the “colony energy” of a given conformation, because each conformation that is generated is viewed as representing a colony of points. The use of the colony energy tends to select conformations that are located in broad energy basins. The approach is applied to the ab initio prediction of the conformations of all of the loops in a dataset of 135 nonredundant proteins. By using an rmsd from a native criterion based on the superposition of loop stems, the average rmsd of 5-, 6-, 7-, and 8-residue long loops is 0.85, 0.92, 1.23, and 1.45 Å, respectively. For 8-residue loops, 60 of 61 predictions have an rmsd of less than 3.0 Å. The use of the colony energy is found to improve significantly the results obtained from the potential function alone. (The loop prediction program, “Loopy,” can be downloaded at http://trantor.bioc.columbia.edu.)
Keywords: force field‖energy minimization‖protein structure prediction
Protein loops are usually defined as segments of the polypeptide chain that do not contain regular units of secondary structure. Although some loops seem to serve as no more than connectors between secondary structure elements, others have been implicated as determinants of protein stability and folding pathways, while others may play important functional roles. The loop prediction problem involves finding the correct conformation for a given loop under the constraint that both ends are fixed through their connection to the rest of the protein. The problem has taken on considerable importance with the increased application of homology modeling methods in protein structure prediction. Although secondary structure elements can, in many cases, be predicted with considerable accuracy because they are often well conserved, sequence and structural variability are integral properties of many loops where, as in the case of antibodies, specificity differences among family members often reside. This variability makes the problem of loop prediction particularly complicated because, by its very nature, homology methods will often not be applicable. Indeed, loop prediction can to some extent be viewed as a mini ab initio folding problem, because the necessary information will not necessarily be found in databases. As such, the problem also serves as an important test of our understanding of the physical chemical principles that determine protein structure.
Two general approaches have been applied to the prediction of loop conformation: database search and ab initio techniques. In the database search method (1–6), a library of segments derived from known protein structures is searched for conformations that fit the topological constraint of the loop stems. The stems correspond to the main-chain atoms that precede and follow the loop, but are not part of the loop itself. Loop candidates found in this way then can be evaluated by different criteria such as sequence relationships between the template and query segment or some measure of conformational energy (7). The database method assumes that the template library contains fragments that are similar to those of the target sequence. In some applications, such methods can be very powerful, for example, when canonical structures exist, as is the case for the hypervariable loops of antibodies (8–9). However, in general, there is no guarantee that the correct loop conformation can be found in the PDB. It has been estimated that only segments of five residues or less are adequately sampled by database methods (10), although a more recent paper (11) found that ab initio generation of conformations becomes more effective for loops of length six or longer. Viijmen and Karplus (12) have pointed out that database search methods can be extended to longer loops if the candidate loops are subsequently evaluated and optimized, in effect increasing the sampling efficiency of these methods. However, a very recent paper (13) obtained average rmsd values for eight-residue loops of only 3.8 Å (7), which is well below the accuracy obtained from recent ab initio methods.
Ab initio methods involve the generation of a large number of loop conformations, usually randomly, and their evaluation based on some sort of energy function (13–16). Loop closure is obtained by using methods such as random tweak (17), energy penalties (18), or analytical closure (19). Loop prediction accuracy depends on the effectiveness of the conformational search procedure and on the quality of the force field used to evaluate the conformational energy. Increased computer power has reduced the problem posed by conformational sampling and, for loops of at least up to 12 residues, conformations close to the native with rmsds of less than 2.0 Å can generally always be found if 2,000 random loops are generated (data not shown; ref. 16). Thus, for loops of this length or less, prediction accuracy depends on the quality of force field.
Although current force fields that account for solvation effects might be expected to pick out the native conformation in a set of randomly generated loops, the native conformation does not always correspond to the conformation of lowest energy (20). Nevertheless, loop prediction accuracy continues to improve with the best results reported in the literature to date corresponding to average rmsds from native of about 1.8 Å as obtained from a superposition of the loop stems (11, 13, 21), which corresponds to about 1.2 Å if the local rmsd measure, involving minimizing the rmsd of loop atoms alone, is used (13).
One issue that complicates most evaluations of conformational free energies is that they do not in general account for loop flexibility. Flexibility is likely to be of particular importance for many loops, and, in some cases, may be associated with their function. More generally, conformations that are located in broad energy basins will be favored for entropic reasons, but this is not accounted for when the energy of a single conformation is calculated. In principle, a search procedure should not be looking for the global energy minimum but rather should attempt to identify a state of lowest free energy in which entropy also is taken into account. A second reason to favor broad energy basins relates to the problem of sampling a large number of conformations. If a large number of states that are close in structure and energy are detected, the probability that other nearby states exist, some of them with even lower conformational energies, should increase.
In this paper, we introduce a new approach to account for the shape of the potential energy curve which is based on a variable that we term the “colony energy.” The colony energy of a state includes a standard energy term, as obtained, for example, from a force field, but it also includes a term that favors conformations that have many neighbors in configurational space. This latter term is derived by assuming that the number of states that surround a particular conformation generated in a sampling procedure is related to the number of other points not sampled that are close to it in conformation. Effectively, we assume that each sampled conformation represents a “colony” of states that are not sampled, and that the size of this colony can be estimated from the number and proximity of neighboring states. The colony energy approach is applied in this paper to the loop prediction problem and, in most cases, is shown to produce an excellent correlation between energy and rmsd from native. Moreover, even the use of a simple force field yields loop predictions that are at least comparable in accuracy to the best results that have been reported in the literature, but at a small fraction of the computer time.
Methods
The Colony Energy.
Suppose we generate N loop candidates such that the ith loop candidate has an energy ΔEi. The energy ΔEi is derived from some force field and may include terms that account for solvent effects as well. The number of conformations in state i, Mi, is given by (22)
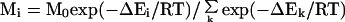 |
1 |
|---|
where k ranges from 1 to M0. M0 is the total number of distinct loops that could in principle exist, most of which are not included in the N states that were generated. Thus, M0 is much larger than N. R is the gas constant, and T is absolute temperature. A given ensemble of loops will obey statistical mechanics if it contains a very large number of conformations. However, in real applications, only a limited number of conformations can be generated so that conformation space will be sparsely sampled. Moreover, regions of conformational space that are heavily populated will, in general, correspond to broad energy basins which would be expected to be favored for entropic reasons, a preference that is not accounted for by the molecular mechanical energy, ΔEi. To account for the existence of loops that are not sampled directly, we assume that each loop that is generated represents other loops that have similar conformations. Thus, the total number of states that the ith loop candidate represents is:
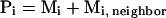 |
2 |
|---|
where Mi, neighbor is the number of neighboring states that are represented by loop candidate i. Si = Rln(Pi) may be interpreted as the entropy associated with broad energy basin-containing conformation i, which also includes contributions from the neighboring states Mi, neighbor. We guess this number by assuming that it is related to the number of neighboring loops that are actually sampled so that
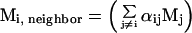 |
3 |
|---|
where j ranges from 1 to N and αij is a function that increases when loops i and j have similar structures. Thus, if loop i has many neighbors with similar conformations that are found by the loop generation procedure, the probability that there are other loops in this region of conformation space will increase. We define αij as
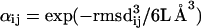 |
4 |
|---|
where rmsdij is the rms deviation in angstroms between loop candidates i and j, L is the number of residues in the loop, and the exponent is defined so as to be dimensionless. The exponent is Eq. 4 provides a measure for the contribution of states in the energy basin centered around conformation i; this is because rmsdij3/6L Å3 may be interpreted as the volume in conformation space divided by the volume per conformation, with proportionality factor 6L determined empirically. The rmsd between two loops is calculated by superimposing their corresponding loop stems. Neither the loop stems nor side chains on the loop are included in the rmsd calculation. Throughout the paper, we used “rmsd” as a measure of prediction accuracy. The calculation of rmsd is carried out in an identical fashion to the calculation of rmsd except that in the former case, a predicted loop is superimposed on the native conformation while in the latter, two predicted loops are superimposed.
The form of the equation given in Eq. 4 is designed so that αij, whose range is between 0 and 1, decreases sharply with increasing rmsd. However, the exact expression for αij is quite arbitrary. Eq. 4 was obtained by optimizing results on four loops (see below).
Substituting Eqs. 1, 3, and 4 into Eq. 2 yields
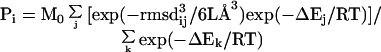 |
5 |
|---|
where j ranges from 1 to N and k from 1 to M0. The first term of Eq. 2 is automatically incorporated into Eq. 5 in the case of j = i.
The total probability of conformations represented by state i, Xi, is given by
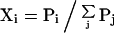 |
6 |
|---|
and the conformational free energy associated with state i is then (see ref. 22)
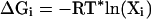 |
7 |
|---|
Substituting Eqs. 5 and 6 into Eq. 7 yields
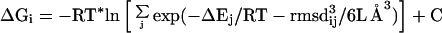 |
8 |
|---|
where j ranges from 1 to N. The constant in Eq. 8 corresponds to the sums over states k and j in Eqs. 5 and 6, respectively. These sums are characteristics of particular loop sets and will have the same value for all loop candidates. Thus, they are ignored in our treatment. Note that the colony energy ΔGi is equal to the force-field energy of loop i, ΔEi, if all other loops have a large rmsd from loop i, but if loop i has many neighbors with low rmsd, then the colony energy will be less than the force-field energy. The more neighboring loops of lower energy that are found, the more loop i will be favored energetically. For rigid loops in steep energy minima, the colony energy will be close to the force-field energy, because the neighboring loops will have a high energy and, thus, will contribute little to the colony energy. The form of the expression for the colony energy is such that it contains an energy term and a term that accounts for the broad energy basin, which in some sense mimics the conformational entropy. Without the rmsd term in Eq. 8, the colony energy ΔGi would be equal to the Gibbs ensemble energy, and all of the loops in the ensemble would have the same value of ΔG. In contrast, the use of the colony energy expression favors loop candidates with many closely related neighbors.
Conformational Energy.
The energy, ΔEj, of loop j should in principle be calculated by using as accurate an expression as possible. In practice, there is usually a tradeoff between accuracy and computational efficiency. In this paper, we have used a simple expression that ignores electrostatic effects but accounts for van der Waals interactions, hydrophobicity, torsional energy, and hydrogen bonding. We chose to ignore electrostatic effects to avoid the need to solve the Poisson–Boltzmann equation for every loop conformation.
The conformational energy is written as
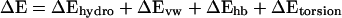 |
9 |
|---|
The hydrophobic energy is evaluated with the expression ΔGhydro = γAT, where γ is 0.025 kcal/mol/Å2 and AT is the solvent-accessible surface area of the protein. Differences in buried surface area between loops are simply reflected in differences in the total surface area. Hydrogen bond energies are evaluated with the method of Stickle et al. (23), where the minimum in the potential well is −0.5 kcal/mol at a distance of 3.0 Å between two heavy atoms (e.g., N and O). Torsional energies, ΔEtorsion, are calculated by using CHARMM22 parameters (24) after side-chains are assembled onto the loop backbone.
We use an expression for the van der Waals energy in which the repulsive term has been softened so as to reduce sensitivity to small changes in atomic positions (16). By trial and error, we arrived at a function (Eq. 10) that fits the CHARMM van der Waals potential curve.
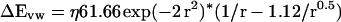 |
10 |
|---|
η is the energy at the minimum of the potential function and is chosen to correspond to the minimum in the van der Waals potential of the CHARMM22 force field between the two interacting atoms, r is the ratio of the interatomic distance and the sum of the van der Waals radii of two interacting atoms.
Test Sets of Loops.
A fair evaluation of loop prediction method requires testing a given method on as many different loops as completely as possible. Here, we use a test set consisting of all loops of length 5–12 residues in a set of 135 proteins compiled by R. L. Dunbrack (available at http://www.fccc.edu/research/labs/dunbrack/culledpdb.html). This set was designed so as to correspond to the smallest group of proteins that represents the entire PDB so that no two proteins have a pairwise sequence identity of greater than 20% and where the resolution of each protein is better than 2.0 Å. The total number of loops of 5, 6, 7, 8, 9, 10, 11, and 12 residues long is 161, 107, 74, 61, 58, 34, 37, and 21, respectively. Loops are defined here as irregular regions connecting two standard secondary structure elements as defined by Database of Secondary Structure in Proteins (25). Hydrogen atoms were added to the proteins with WHATIF (26), where heavy atoms are fixed at their original positions. The expression for αij (Eq. 4) was optimized to yield low rmsds for four loops in the protein ribonuclease-A (1rat; residue from 12 to 23 and from 63 to 70) and proteinase inhibitor (5pti; from residue 6 to 16 and from 35 to 43). The optimized rmsds for these four loops are 2.62, 0.53, 0.96 and 0.60 Å for loop 12–23, 63–70 in 1rat, and 6–16 and 35–43 in 5pti, respectively.
Loop Prediction Procedure.
Our loop prediction procedure begins with the generation of 2,000 random backbone conformations that are closed with the random tweak method (17). For each loop candidate, side chains are assembled onto the backbone with the side-chain prediction program SCAP, in which a 40° rotamer library compiled from 135 proteins is used (27). The 2,000 loop candidates then are subjected to an energy minimization by using a simplified force field consisting only of the softened van der Waals energy, ΔEvw, given in Eq. 10. We use a fast torsional minimizer (Z.X. and B.H., unpublished work) that can find the minimum of an eight-residue loop in less than 0.1 seconds on an SGI R10000. After the initial minimization, the 1,000 lowest energy conformations are retained. The colony energy ΔG is calculated for each of the 1,000, and of these, 30% survive for the next step.
Pairs of loops with rmsd (in Å) greater than L/10 and less than L (L is the number of residues of the loop) are then combined (i.e., for an eight-residue loop, the first four residues in one loop are combined with the last four in another) to form a new loop that is fused in the middle with the “random tweak” procedure. This process produces a new set of loops in addition to the original 300 loops that were retained. Of this new set, the lowest-energy 30% again survive, and the procedure is repeated until a single loop remains or the number of iteration steps is greater than 5. In any of the above steps, no more than 300 loops are allowed to survive to the next generation. The entire procedure takes about 20 min for a loop of eight residues.
Results
Details of Application to a Single Loop.
In this section, the colony energy approach is applied to the loop involving residues 64–71 in ribonuclease-A (1rat-A). This loop is one of four used to optimize the expression for αij. The loop is on the protein surface and protrudes into the solvent so that there are few geometric restrictions that limit the direction in which the loop points. We did not consider the disulfide bond between Cys-65 and Cys-72, although taking account of this bond would dramatically simplify the prediction problem for this loop.
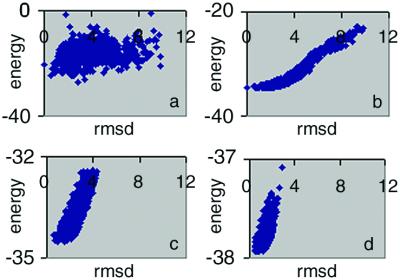
Fig. 1a plots ΔE vs. rmsd for the 1,000 lowest energy loop conformations generated as described above. It is evident that no correlation exists. The native conformation has energy of −20.45 kcal/mol, ranking 86th of the 1,000 loop candidates. The loop candidate with the lowest rmsd, 0.53 Å, has an energy of −24.3 kcal/mol, 3.1 kcal/mol greater than the loop of the lowest energy (rmsd 2.84 Å). Most of loops have energies between −10 and −20 kcal/mol and have rmsds between 2 and 4 Å. The 20 lowest energy loops in Fig. 1a have average rmsds of 2.3 Å. Fig. 1b contains a comparable plot of the colony energy, ΔG, vs. rmsd. The difference between the two plots is dramatic. As opposed to the result when the force-field energy is used (Fig. 1a), there is a strong correlation between colony energy and rmsd. The loop with the lowest colony energy (−34.6 kcal/mol) has an rmsd of 1.49 Å, whereas the best loop candidate (rmsd of 0.53 Å) has colony energy −34.4 kcal/mol. Furthermore, the reliability of the prediction has significantly increased because almost all of the lower energy loops have low rmsd. For example, the 20 lowest energy loops now have an average rmsd 1.5 Å, significantly below the 2.3 Å mentioned above. The native conformation has colony energy of −34.5 kcal/mol, only 0.1 kcal/mol higher than the lowest energy loop.
Figure 1.
Colony energy analysis for loops 63–70 in ribonuclease-A (1rat). (a) Plot of energy vs. rmsd for the candidate loops. The native conformation is the point on the y axis. (b) Plot of colony energy vs. rmsd for the loops shown in a. The native conformation is also on the y axis. (c) Colony energy vs. rmsd for the loops generated from the loop fusion procedure applied to the loops in b. (d) The colony energy–rmsd plot after three iterations of loop–loop fusion and colony energy sorting.
Fig. 1c plots ΔG vs. rmsd for loops generated with the loop-fusion procedure applied to the lowest energy 300 loops from Fig. 1b. The colony energy of each of the 4,356 loops generated in this way then was calculated and, of these, the 1,000 loops with the lowest colony energy were plotted in Fig. 1c. The loop with the lowest colony energy has an rmsd of 0.89 Å. Three more iterations yields Fig. 1d, where the lowest colony energy structure has an rmsd of only 0.57 Å.
Loop Prediction for 135 Proteins.
The same procedure was applied to each of the 5 to 12 residue loops in the 135 proteins listed by Dunbrack. The average rmsd for these loops is listed in Table 1, where the average is obtained by dividing the sum of the rmsds of all loops of length L by the total number of loops of that length. Three averages are provided: (i) rmsd without the use of colony energy; (ii) rmsd using the colony energy; and (iii) rmsd using the colony energy but ignoring side chains (no atoms beyond Cβ). It is clear from the table that the colony energy improves prediction accuracy for all loop lengths (that the predictions for some longer loops are better than for some shorter loops is likely to be an artifact of sample size).
Table 1.
Loop prediction accuracy for 135 proteins
| L | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
|---|---|---|---|---|---|---|---|---|
| N | 161 | 107 | 74 | 61 | 58 | 34 | 37 | 21 |
| rmsd(a) | 1.21 | 1.28 | 1.46 | 1.99 | 3.06 | 2.97 | 3.68 | 3.81 |
| rmsd(b) | 0.85 | 0.92 | 1.23 | 1.45 | 2.68 | 2.21 | 3.52 | 3.42 |
| rmsd(c) | 0.95 | 1.10 | 1.58 | 1.89 | 2.95 | 3.01 | 3.69 | 3.50 |
As shown in Table 1, including side chains has little effect on prediction accuracy for short and longer loops, but has a somewhat large effect for medium loops. For loops of length less than 6 and greater than 11, including side chains only improves results by ≈0.2 Å; for medium loops of length between 7–10, side chains have a larger effect. Accuracy decreases by .43 Å when side chains are ignored for 8 residue loops and by only 0.08 Å for 12 residue loops. The reason may be that for short loops, the stem constraints are already strong enough to define the loop conformation, whereas for longer loops, the large rmsd of the backbone (≈3.5 Å even with side chains considered) makes side-chain prediction highly inaccurate. The results for longer loops may also be because of an insufficient number of loops to allow for meaningful averages.
Results for all 61 of the 8 residue loops tested here are listed in Table 2. Two rmsd values are listed for each loop and correspond to the rmsd values without use of the colony energy (next to last column) and with the colony energy (last column). When the colony energy is used, only 1 of the 61 loops have rmsds greater than 3.0 Å. For loops of eight residues, an rmsd of less than 3.0 Å usually implies that the loop points in the same direction as the native conformation. To determine the effect of geometric restraints on prediction accuracy, the percent of each loop that is exposed relative to the isolated loops, s, and, d, the distance between the two Cα atoms of the stem residues of a loop, are listed in the table. In general, the expectations that buried loops (small s) or long loops (large d) are more accurately predicted are borne out by the results listed in Table 2. The loop with the largest value of d (21.7 Å), on protein oxidoreductase (1nif) 279–286, was predicted quite accurately with an rmsd of 0.31 Å, the second best in the list. The only prediction with rmsd larger than 3.0 Å is for a loop on the protein transferees 1btk (133–140), which has the largest value of s (25.3%).
Table 2.
Prediction results for each of the eight residue loops
| PDB entry | Loop | s | d | rmsd1 | rmsd2 |
|---|---|---|---|---|---|
| 1cbn | 18–25 | 24.09 | 12.67 | 1.18 | 1.04 |
| 1nls | 97–104 | 11.51 | 8.79 | 1.30 | 0.81 |
| 1cex | 73–80 | 11.78 | 13.32 | 0.92 | 0.87 |
| 1amm | 69–76 | 15.06 | 15.71 | 1.79 | 1.85 |
| 1amm | 81–88 | 16.78 | 13.72 | 3.10 | 1.92 |
| 1amm | 158–165 | 12.45 | 15.44 | 1.19 | 1.15 |
| 1arb | 136–143 | 14.24 | 16.13 | 2.02 | 2.01 |
| 1arb | 212–219 | 16.59 | 12.89 | 0.48 | 0.86 |
| 1arb | 249–256 | 18.08 | 9.68 | 1.68 | 1.62 |
| 1msi | 26–33 | 16.42 | 9.79 | 2.47 | 2.16 |
| 7rsa | 64–71 | 22.71 | 6.88 | 0.77 | 1.67 |
| 1c52 | 97–104 | 19.61 | 16.65 | 2.50 | 1.32 |
| 1rro | 18–25 | 18.10 | 7.83 | 0.63 | 0.31 |
| 1aac | 48–55 | 11.33 | 14.11 | 0.45 | 0.53 |
| 1plc | 6–13 | 18.10 | 4.94 | 7.54 | 1.68 |
| 1plc | 32–39 | 7.18 | 13.24 | 1.84 | 1.87 |
| 5ptp | 22–29 | 8.25 | 12.85 | 2.13 | 1.79 |
| 5ptp | 172–179 | 15.46 | 14.14 | 1.47 | 0.63 |
| 5p21 | 144–151 | 14.19 | 4.51 | 0.64 | 0.76 |
| 1rhs | 235–242 | 20.52 | 14.72 | 0.44 | 0.92 |
| 1awd | 56–63 | 16.23 | 12.04 | 1.33 | 1.21 |
| 2ctc | 53–60 | 16.31 | 10.63 | 3.35 | 2.91 |
| 1aba | 7–14 | 19.23 | 6.13 | 2.42 | 2.05 |
| 1vwj (chain B) | 45–52 | 21.34 | 5.43 | 7.78 | 2.89 |
| 3seb | 40–47 | 13.94 | 12.74 | 0.96 | 0.64 |
| 1brt | 205–212 | 10.15 | 14.88 | 0.77 | 0.68 |
| 1ezm | 92–99 | 14.25 | 16.95 | 0.52 | 0.96 |
| 1ezm | 105–112 | 15.28 | 10.86 | 2.23 | 1.92 |
| 1kpf | 105–112 | 8.90 | 12.78 | 2.51 | 2.44 |
| 1opd | 8–15 | 14.04 | 10.79 | 3.37 | 0.43 |
| 2arc (chain A) | 28–35 | 17.53 | 11.70 | 3.09 | 1.87 |
| 5icb | 15–22 | 22.44 | 8.66 | 2.51 | 1.37 |
| 1a62 | 70–77 | 19.33 | 11.36 | 2.80 | 1.66 |
| 1a62 | 102–109 | 23.73 | 11.52 | 4.57 | 2.44 |
| 1lit | 82–89 | 20.37 | 4.64 | 4.99 | 0.92 |
| 1ra9 | 51–58 | 17.60 | 14.93 | 2.52 | 2.27 |
| 1hfc | 119–126 | 16.05 | 14.98 | 0.62 | 0.73 |
| 1nox | 99–106 | 18.59 | 14.93 | 3.02 | 2.80 |
| 1a1h | 107–114 | 26.55 | 5.92 | 2.70 | 0.68 |
| 1a3c | 92–99 | 17.61 | 12.54 | 3.42 | 2.57 |
| 1ads | 274–281 | 15.44 | 17.32 | 1.39 | 1.29 |
| 1aru | 234–241 | 4.67 | 7.72 | 0.36 | 0.49 |
| 1btk (chain A) | 67–74 | 18.98 | 16.86 | 2.46 | 2.11 |
| 1btk (chain A) | 133–140 | 25.33 | 12.79 | 3.35 | 3.31 |
| 1cvl | 148–155 | 17.85 | 10.40 | 1.74 | 1.40 |
| 1cvl | 229–236 | 20.27 | 14.10 | 1.95 | 1.80 |
| 1dad | 176–183 | 22.63 | 12.51 | 3.38 | 1.33 |
| 1dim | 246–253 | 7.85 | 9.16 | 0.79 | 0.64 |
| 1mrp | 68–75 | 10.26 | 19.99 | 0.66 | 0.57 |
| 1nfp | 118–125 | 19.63 | 17.60 | 2.62 | 2.55 |
| 1nif | 221–228 | 5.18 | 10.49 | 0.75 | 1.99 |
| 1nif | 279–286 | 12.58 | 21.74 | 0.32 | 0.31 |
| 1nwp (chain A) | 84–91 | 11.41 | 11.68 | 1.04 | 1.27 |
| 1ppn | 101–108 | 16.33 | 19.89 | 0.60 | 0.46 |
| 1ppn | 191–198 | 18.25 | 7.07 | 2.34 | 2.34 |
| 1wer | 824–831 | 10.65 | 18.80 | 1.03 | 1.32 |
| 1wer | 916–923 | 18.79 | 16.67 | 1.27 | 1.71 |
| 2ayh | 124–131 | 17.09 | 12.89 | 0.59 | 0.61 |
| 2ayh | 194–201 | 15.54 | 17.74 | 2.68 | 2.60 |
| 2dri | 64–71 | 6.26 | 9.36 | 0.95 | 1.29 |
| 3nul | 36–43 | 20.39 | 17.47 | 0.87 | 0.45 |
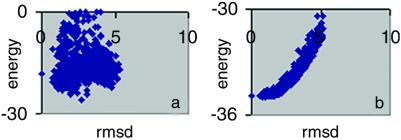
Comparison of the two rmsd values in Table 2 reveals that the colony energy improves prediction accuracy in 44 of the 61 loops. In many cases, the effect is quite dramatic. For the 17 cases where colony energy lowers prediction accuracy, the effect is generally very small, except for loops 221–228 in oxidoreductase (1nif), where the accuracy drops from 0.75 Å to 1.99 Å. The success of the colony energy model results from the good correlation it yields between energy and rmsd. Figs. 2a and b show another example of the effect of colony energy on the rmsd–energy correlation for one of the loops (96–103 in 1c52, an electron transport protein) in the test set. Use of the colony energy increases prediction accuracy from rmsd 2.50 to 1.60 Å. Another two rounds of loop fusion brings the rmsd down to 1.32 Å. In Fig. 2a, the native conformation has an energy of −18.1 kcal/mol, 7.7 kcal/mol higher than the loop with the lowest energy, which has an rmsd 2.50 Å. However, the colony energy of the native conformation is very close to the lowest energy with difference of 0.05 kcal/mol. Although the use of the colony energy increases prediction accuracy, there are a few examples where this is not the case, as shown in Table 2. However, even in these cases, the reduction in accuracy is generally quite small.
Figure 2.
Colony energy analysis for loops 96–103 of 1c52, an electron transport protein. Fig. 1 a and b captions also apply to Fig. 2 a and b, respectively.
Discussion
In this paper, we have described a method to introduce the shape of the potential energy curve into the evaluation of conformational energies. The method, which involves the definition of a variable that we term the colony energy, can be applied to any problem involving the sampling of many different conformations. The colony energy is designed to become more negative for conformations that have many neighbors with low rmsd. The effectiveness of our approach is demonstrated with specific applications to the problem of loop prediction in proteins. Results obtained by using a very simple force field constitute an improvement over the best results reported in the literature (13) but at a fraction of the computational cost. For example, for eight-residue loops, it takes about 20 min to achieve an average accuracy of 1.45 Å.
Given the ability of the colony energy expression to improve the accuracy of loop prediction, it is of interest to consider whether its success is based on some underlying physical principle. The form of Eq. 8 is such that the colony energy does not identify the global energy minimum but rather favors loop candidates that not only have low energies but that also are located in broad energy basins. An appealing explanation for its effects is that the colony energy captures some elements of loop flexibility and, hence, accounts for conformational entropy. Entropy effects also can be estimated analytically from the matrix of second derivatives of the energy (28). Another important feature of the colony energy that is evident from the form of the expression given in Eq. 8 is that it effectively smoothes out the force-field energy, lowering the energy of high-energy conformations that are close in structure to low-energy conformations (this is the reason the colony energy vs. rmsd plots are so smooth). A number of techniques are available to smooth the energy surface so as to facilitate the search for the global minimum (reviewed in refs. 29–31). In contrast, the colony energy approach averages the conformational probability surface directly. This averaging procedure has the effect of both creating broad energy basins when many nearby states are detected but also of keeping conformations whose high energy is caused by inadequate sampling or random errors in the force field. Such conformations are located in a low-energy region of the potential energy surface (because they have a low energy neighbor) and should not necessarily be discarded. Also, it is possible that the colony energy corrects in some way for a deficiency in the energy function we have used. In principle, one might expect that the accuracy of our predictions would improve if we used a more accurate force field, but this possibility still needs to be tested. A much needed refinement is the addition of electrostatic and solvation effects to the model we present.
Also, it is possible to view the colony energy as an effective heuristic that favors conformations with many neighbors and which improves loop prediction. Shortle et al. (32) used rmsds to cluster low-energy conformations and found that those with the largest number of neighbors tended to be closest to the native conformation. This result was used to argue that native conformations may be located in broad energy basins. The current work is consistent with these ideas but, in addition, incorporates features of the energy basin directly into the evaluation of the conformational free energy. Huber and van Gunsteren (33) reported the SWARM-MD method, which uses an rmsd-dependent force to drive molecular dynamics trajectories toward an average trajectory. This procedure has the effect of speeding up convergence to the lowest energy conformation. In contrast, the colony energy approach consists of a sampling procedure that includes a bias toward probability-weighted clusters of states which thus accounts for both conformational energy preferences and for entropic effects. The approach is inherently fast because the final prediction is based on the statistical distribution of all of the initial conformations.
In the paper, we generated 2,000 loop candidates for each loop. For short loops of less than 7 residues, 500 loop candidates are enough to produce results of comparable accuracy, to within about 0.1 Å to those reported here. For longer loops of more than 10 residues, 2,000 loop candidates seem not to be enough. For example, prediction accuracy was improved from 3.42 to 3.25 Å when 4,000 instead of 2,000 initial loop candidates were used for 12 residue loops (data not shown). However, using 6,000 initial loop candidates for 12 residue loops led to a slight decrease (0.1 Å) in prediction accuracy relative to the use of 4,000 candidates. The major problem, as discussed above, is likely to be inadequacies in the potential function whose effects become more noticeable for longer loops with fewer geometric constraints.
We anticipate that the colony energy concept will prove useful in many other applications, such as side-chain prediction and homology model building. Different expressions for αij would probably have to be used and indeed, for loop prediction, it may be empirically possible to obtain expressions for αij that depend on the properties of the loop being treated. Thus, although the approach presented in this work has been quite successful in applications to loop prediction, future developments may make it possible to obtain even better results in this and other applications.
Acknowledgments
We thank Drs. Matthew Jacobson, Avinoam Ben-Shaul, Richard Friesner, Joon Jung, Emil Alexov, Jan Norberg, and Lei Xie for many stimulating discussions and for their insightful comments on the manuscript. This work was supported by National Institutes of Health Grant GM-30518.
Abbreviation
rmsd
rms deviation
References
- 1.Greer J. Proc Natl Acad Sci USA. 1980;77:3393–3397. doi: 10.1073/pnas.77.6.3393. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Ring C S, Kneller D G, Langridge R, Cohen F E. J Mol Biol. 1992;224:685–699. doi: 10.1016/0022-2836(92)90553-v. [DOI] [PubMed] [Google Scholar]
- 3.Tramontano A, Lesk A M. Proteins. 1992;13:231–245. doi: 10.1002/prot.340130306. [DOI] [PubMed] [Google Scholar]
- 4.Kwasigroch J M, Chomilier J, Mornon J P. J Mol Biol. 1996;259:855–872. doi: 10.1006/jmbi.1996.0363. [DOI] [PubMed] [Google Scholar]
- 5.Donate L E, Rufino S D, Canard L H, Blundell T L. Protein Sci. 1996;5:2600–2616. doi: 10.1002/pro.5560051223. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Oliva B, Bates P A, Querol E, Aviles F X, Sternberg M J. J Mol Biol. 1997;266:814–830. doi: 10.1006/jmbi.1996.0819. [DOI] [PubMed] [Google Scholar]
- 7.Wojcik J, Mornon J P, Chomilier J. J Mol Biol. 1999;289:1469–1490. doi: 10.1006/jmbi.1999.2826. [DOI] [PubMed] [Google Scholar]
- 8.Chothia C, Lesk A M. J Mol Biol. 1987;196:901–917. doi: 10.1016/0022-2836(87)90412-8. [DOI] [PubMed] [Google Scholar]
- 9.Martin A C, Thornton J M. J Mol Biol. 1996;263:800–815. doi: 10.1006/jmbi.1996.0617. [DOI] [PubMed] [Google Scholar]
- 10.Fidelis K, Stern P S, Bacon D, Moult J. Protein Eng. 1994;7:953–960. doi: 10.1093/protein/7.8.953. [DOI] [PubMed] [Google Scholar]
- 11.Deane C M, Blundell T L. Protein Sci. 2001;10:599–612. doi: 10.1110/ps.37601. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Van Vlijmen H W, Karplus M. J Mol Biol. 1997;267:975–1001. doi: 10.1006/jmbi.1996.0857. [DOI] [PubMed] [Google Scholar]
- 13.Fiser A, Do R, Sali A. Protein Sci. 2000;9:1753–1773. doi: 10.1110/ps.9.9.1753. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Go N, Scheraga H A. Macromolecules. 1970;3:178–187. [Google Scholar]
- 15.Bruccoleri R E, Karplus M. Biopolymers. 1990;29:1847–1862. doi: 10.1002/bip.360291415. [DOI] [PubMed] [Google Scholar]
- 16.Rapp C S, Friesner R A. Proteins. 1999;35:73–83. [PubMed] [Google Scholar]
- 17.Shenkin P S, Yarmush D L, Fine R M, Wang H J, Levinthal C. Biopolymers. 1987;26:2053–2085. doi: 10.1002/bip.360261207. [DOI] [PubMed] [Google Scholar]
- 18.Collura V, Higo J, Garnier J. Protein Sci. 1993;2:1502–1510. doi: 10.1002/pro.5560020915. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Wedemeyer W, Scheraga H A. J Comp Chem. 1999;20:819–844. doi: 10.1002/(SICI)1096-987X(199906)20:8<819::AID-JCC8>3.0.CO;2-Y. [DOI] [PubMed] [Google Scholar]
- 20.Smith K C, Honig B. Proteins. 1994;18:119–132. doi: 10.1002/prot.340180205. [DOI] [PubMed] [Google Scholar]
- 21.Galaktionov S, Nikiforovich G V, Marshall G R. Biopolymers. 2001;60:153–168. doi: 10.1002/1097-0282(2001)60:2<153::AID-BIP1010>3.0.CO;2-6. [DOI] [PubMed] [Google Scholar]
- 22.Greiner W, Stocker H, Neise L. Thermodynamics and Statistical Mechanics. Berlin: Springer; 1995. [Google Scholar]
- 23.Stickle D F, Presta L G, Dill K A, Rose G D. J Mol Biol. 1992;226:1143–1159. doi: 10.1016/0022-2836(92)91058-w. [DOI] [PubMed] [Google Scholar]
- 24.Mackerell A D., Jr J Phys Chem B. 1998;102:3586–3616. doi: 10.1021/jp973084f. [DOI] [PubMed] [Google Scholar]
- 25.Kabsch W, Sander C. Biopolymers. 1983;22:2577–2637. doi: 10.1002/bip.360221211. [DOI] [PubMed] [Google Scholar]
- 26.Vriend G. J Mol Graphics. 1990;8:52–56. doi: 10.1016/0263-7855(90)80070-v. [DOI] [PubMed] [Google Scholar]
- 27.Xiang Z, Honig B. J Mol Biol. 2001;311:421–430. doi: 10.1006/jmbi.2001.4865. [DOI] [PubMed] [Google Scholar]
- 28.Go N, Scheraga H A. J Chem Phys. 1969;51:4751–4767. [Google Scholar]
- 29.Wales D J, Scheraga H A. Science. 1999;285:1368–1372. doi: 10.1126/science.285.5432.1368. [DOI] [PubMed] [Google Scholar]
- 30.Pappu R V, Marshall G R, Ponder J W. Nat Struct Biol. 1999;6:50–55. doi: 10.1038/4922. [DOI] [PubMed] [Google Scholar]
- 31.Pillardy J, Piela L. J Comput Chem. 1997;18:2040–2049. [Google Scholar]
- 32.Shortle D, Simons K T, Baker D. Proc Natl Acad Sci USA. 1998;95:11158–11162. doi: 10.1073/pnas.95.19.11158. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Huber T, van Gunsteren W F. J Phys Chem A. 1998;102:5937–5943. [Google Scholar]