Multilocus Linkage Tests Based on Affected Relative Pairs (original) (raw)
Abstract
For complex diseases, recent interest has focused on methods that take into account joint effects at interacting loci. Conditioning on effects of disease loci at known locations can lead to increased power to detect effects at other loci. Moreover, use of joint models allows investigation of the etiologic mechanisms that may be involved in the disease. Here we present a method for simultaneous analysis of the joint genetic effects at several loci that uses affected relative pairs. The method is a generalization of the two-locus LOD-score analysis for affected sib pairs proposed by Cordell et al. We derive expressions for the relative risk, λ_R_, to a relative of an affected individual, in terms of the additive and epistatic components of variance at an arbitrary number of disease loci, and we show how these can be used to fit a likelihood model to the identity-by-descent sharing among pairs of affected relatives in extended pedigrees. We implement the method by use of a stepwise strategy in which, given evidence of linkage to disease at _m_-1 locations on the genome, we calculate the conditional likelihood curve across the genome for an _m_th disease locus, using multipoint methods similar to those proposed by Kruglyak et al. We evaluate the properties of our method by use of simulated data and present an application to real data from families with insulin-dependent diabetes mellitus.
Introduction
In recent years, several methods have been proposed for the simultaneous detection of multiple loci involved in complex diseases. These include model-based methods, in which a detailed model is specified for the disease mode of inheritance, and nonparametric—or model-free—methods, in which details such as allele frequencies and penetrance functions for the disease are not specified (Elston 1998). Model-based methods include the two-locus LOD-score method described by Lathrop and Ott (1990) and Schork et al. (1993). Model-free methods include the sib-pair methods of Dizier and Clerget-Darpoux (1986) and Knapp et al. (1994), the two-locus marker-association-segregation χ2 (MASC) method (Dizier et al. 1994), the two-locus maximum LOD score or maximum-likelihood statistic (MLS) (Cordell et al. 1995; Farrall 1997; Olson 1997) or score statistic (Dupuis et al. 1995), and the two-locus weighted pairwise correlation (WPC) method (Zinn-Justin and Abel 1998). Recently, Cox et al. (1998), Strauch et al. (1998), Xu et al. (1998), and Cordell et al. (1999) have further investigated the use of increasing the power to detect an effect by conditioning on an effect at a previously identified disease-gene location. Although all of these methods are ultimately aimed at detection of effects at multiple interacting loci, in practice they have normally been restricted to the analysis of no more than two loci, because of either theoretical or computational constraints. In addition, the methods proposed by Dizier and Clerget-Darpoux (1986), Knapp et al. (1994), and Cordell et al. (1995) are restricted to sib pairs or affected sib pairs (ASPs), which may be a convenient unit of sampling but which means that we discard information from other affected relatives when they are available. The methods of Lathrop and Ott (1990) and Zinn-Justin and Abel (1998), although not restricted to sib pairs, require specification of the true (two-locus) genetic model or class of models. In addition, the model-based approach of Lathrop and Ott (1990) and Schork et al. (1993) involves a large and sometimes infeasible computational burden.
We should distinguish between those methods whose primary focus is the detection of disease loci and those whose focus is to model the interaction of disease loci. These two goals are clearly interrelated, but which goal is the primary focus is not always clear from the methodology. In the present study, we take, as our primary aim, the detection of disease loci in the presence of epistatic interactions, while noting that the methods we describe may also, under certain circumstances, be used to test specific hypotheses concerning the interactions. This is in the spirit of approaches proposed by Elston (1995) and Tiwari and Elston (1997), for analysis of two-locus quantitative traits. Cox et al. (1998), Xu et al. (1998), and Cox et al. (1999) have recently proposed a method that involves weighting a family's contribution to the test statistic at one locus according to the magnitude of the family’s contribution to the test statistic at another locus. Although this is a potentially appealing way of conditioning on a known locus, the choice of weighting scheme may be problematic and may not necessarily reflect a feasible genetic model, yet some properties of the true genetic model (e.g., heterogeneity or epistasis) must be assumed, to generate the weights. The method is reminiscent of simply selecting one’s data according to either identity-by-descent (IBD) sharing or the genotypes possessed at a known locus. Although this has been a useful means for the detection of some effects—for example, at IDDM4 conditioned on IDDM1 in type 1 diabetes (Davies et al. 1994; Mein et al. 1998)—this procedure is rather arbitrary. It is not clear, for example, whether the data should be subdivided into families sharing 2 alleles IBD and families sharing 1 or 0 alleles IBD at the known locus or into families sharing 0 alleles IBD and families sharing 1 or 2 alleles IBD at this locus. If tests are performed in several subsamples of families, they may need to be corrected for multiple testing—for example, by use of a Bonferroni correction, which will reduce the significance of any result. Furthermore, even if a second locus does exist, the procedure may in fact result in an observed decrease—rather than an increase—in significance, because of the decrease in the effective sample size in each subsample.
In contrast, the method proposed in the present study is a generalization of the two-locus MLS method (Cordell et al. 1995), which is based on IBD allele sharing at several loci. Linkage tests that are based on allele sharing (Weeks and Lange 1988; Risch 1990_a_, 1990_b_; Whittemore and Halpern 1994) are a popular alternative to traditional model-based linkage analysis when mapping susceptibility genes for complex traits, since they require no explicit prior specification of the inheritance model. In recent years, Kruglyak and Lander (1995) and Kruglyak et al. (1996) have developed algorithms that extract the full multipoint inheritance information from pedigrees of moderate size, allowing IBD sharing among pairs or sets of relatives to be probabilistically inferred across the whole genome. These calculations have been incorporated into the computer programs GENEHUNTER and MAPMAKER/SIBS, for analysis of extended pedigrees and affected sib pairs, respectively. Although the inheritance pattern extracted by GENEHUNTER represents the fullest possible inheritance information available from a pedigree (under the assumption of no interference), there are some problems with the linkage test proposed by Kruglyak et al. (1996). First, the test has been shown to be conservative when the descent information is incomplete (Kruglyak et al. 1996; Kong and Cox 1997). Second, the general shape of the “nonparametric linkage” (NPL) curve obtained tends to decrease between markers, because information is more incomplete for a location midway between two markers than it is for a location close to a marker. This contrasts with the results from model-based (parametric) LOD-score analysis and with those from MAPMAKER/SIBS. In fact, the results from GENEHUNTER do not necessarily bear any direct relationship to the results from MAPMAKER/SIBS, even if only nuclear families are used, since the statistics used in GENEHUNTER are based on the scoring functions discussed by Whittemore and Halpern (1994), rather than on the likelihood-based statistics proposed by Risch (1990_a_, 1990_b_) and used in MAPMAKER/SIBS. This is somewhat unsatisfactory, since we would prefer our results for extended pedigrees to be a generalization of those for sib pairs.
Kong and Cox (1997) have proposed an alternative one-parameter linkage test that addresses many of the problems with the tests proposed by Kruglyak et al. (1996). In particular, their method is more powerful than that of Kruglyak et al. (1996), and it produces NPL curves that conform in shape to traditional model-based LOD-score curves. However, the method proposed by Kong and Cox (1997), although likelihood based, is not directly equivalent to the ASP likelihood-ratio statistic of Risch (1990_a_, 1990_b_), unless additional parameters are included.
Here, in contrast, we propose a generalization of the MLS statistic for ASPs that was proposed by Risch (1990_a_; 1990_b_), using all pairs of affected relatives in a pedigree. It has been shown (Cordell et al. 1995; Dupuis et al. 1995) that, with an MLS or score approach, the power to detect effects at unlinked loci is increased by use of two-locus methods, provided that the true genetic model is not multiplicative, as defined by Risch (1990_a_). If the true genetic model is multiplicative, then the two-locus MLS for two unlinked loci is equal to the sum of the individual single-locus MLSs at the two loci, and no further significance is achieved by modeling the joint action of the loci. However, the initial significances at the individual loci will not be decreased. The MLS approach allows immediate generalization to models that involve an arbitrary number of disease loci via an extension of the methods described by Cordell et al. (1995) and Farrall (1997). All that is required is to be able to calculate the prior and posterior probabilities that each affected relative pair shares i alleles IBD (_i_=0,1,2) at particular locations on the genome. By use of the term “prior probabilities,” we mean probabilities that are based purely on relationship, whereas, by use of the term “posterior probabilities,” we mean probabilities that are conditional on both relationship and marker data.
Methods
For the _j_th affected pair of relatives in a pedigree, define w ij to be the probability of the observed marker data, given that the pair share i alleles IBD at a single marker locus. Risch (1990_c_) showed that, for ASPs, the likelihood may be written as 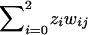 , where z i is the population parameter (to be estimated) that corresponds to the probability that an ASP shares i alleles IBD at the marker. Under the null hypothesis that the marker is unlinked to disease, the parameters (_z_0,_z_1,_z_2) should take the values (.25,.5,.25) that correspond to the Mendelian probabilities of a random sib pair sharing 0, 1, or 2 alleles IBD. By defining f i to be the prior probabilities (.25,.5,.25) and by defining
, where z i is the population parameter (to be estimated) that corresponds to the probability that an ASP shares i alleles IBD at the marker. Under the null hypothesis that the marker is unlinked to disease, the parameters (_z_0,_z_1,_z_2) should take the values (.25,.5,.25) that correspond to the Mendelian probabilities of a random sib pair sharing 0, 1, or 2 alleles IBD. By defining f i to be the prior probabilities (.25,.5,.25) and by defining 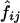 to be the posterior probabilities, given the observed marker data of the _j_th pair sharing i alleles IBD, then, by use of Bayes theorem, we may write the likelihood for pair j as
to be the posterior probabilities, given the observed marker data of the _j_th pair sharing i alleles IBD, then, by use of Bayes theorem, we may write the likelihood for pair j as
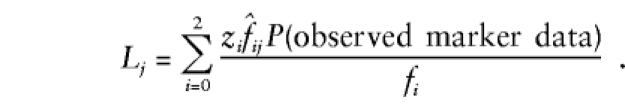
Similarly, for an m locus-disease model, the likelihood for the _j_th ASP may be written as
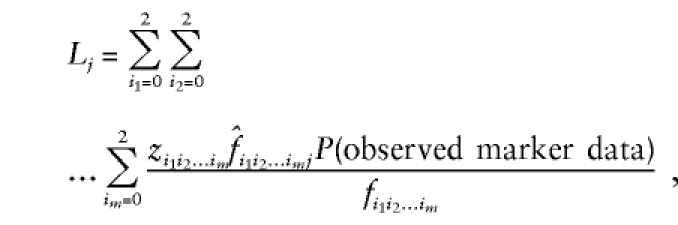
where now z i_1_i_2…_i m, 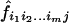 , and f i_1_i_2…_i m refer to the same sharing probabilities but at the m loci simultaneously—for example, _z_00…0 is the probability that an ASP shares 0 alleles IBD at each of the m loci. These expressions for the likelihood lead to the following expression for the log-likelihood–ratio test statistic (MLS) for testing of the null hypothesis that the m loci are all unlinked to disease:
, and f i_1_i_2…_i m refer to the same sharing probabilities but at the m loci simultaneously—for example, _z_00…0 is the probability that an ASP shares 0 alleles IBD at each of the m loci. These expressions for the likelihood lead to the following expression for the log-likelihood–ratio test statistic (MLS) for testing of the null hypothesis that the m loci are all unlinked to disease:
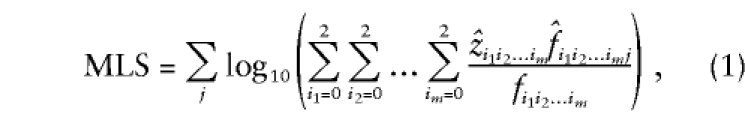
where the 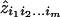 are maximum-likelihood estimates of the relevant sharing probabilities.
are maximum-likelihood estimates of the relevant sharing probabilities.
This equation is, in fact, quite general, since, by defining the probabilities f i_1_i_2…_i m j and z i_1_i_2…_i m j as the relevant sharing probabilities for relative pair j, which may be of varying type (e.g., sibs, cousins, uncle-nephew etc.), we can use essentially the same expression,
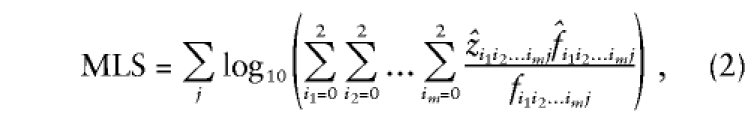
as a test of the same null hypothesis, using data from a sample of affected relative pairs of varying types. If the sharing between pairs is independent, then this is a valid test statistic, since the likelihood for the whole data set is the product of the likelihoods for each pair. Meunier et al. (1997) and Greenwood and Bull (1999) have shown that, for a single locus and with both parents typed, this is approximately valid (giving a slight increase in type 1 error) when all possible (nonindependent) pairs from a nuclear family are used in an ASP study. However, for extended family data, it is not clear whether this result will still hold, since the correlation between pairs may be much greater. We therefore consider using (2) as a pseudolikelihood, and we estimate significance levels by using simulation rather than by relying on asymptotic results.
In the Appendix, we show that the z i_1_i_2…_i m j, estimated by 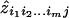 in (2), may be written in terms of the prior probabilities f i_1_i_2…_i m j and the 3_m_-1 underlying additive and dominance variances caused by the m disease-causing loci (divided by a constant). The MLS may therefore be written in terms of the variance components (divided by a constant) and the prior and posterior probabilities of the IBD sharing at the m loci. For all relatives, these probabilities can be calculated at increments across the genome, by use of the inheritance-vector distribution (Kruglyak et al. 1996). By maximizing the likelihood with respect to the variance component parameters, rather than with respect to the z i_1_i_2…_i m j, we may fit specific classes of genetic models to the data—for example, single-locus models, two-locus models, three-locus models, etc. Note that the “possible triangle” restrictions on the _z_s (Holmans 1993) will automatically be satisfied by restriction of the variance components to nonnegative quantities. When more than one disease locus is considered, we may set the second- or higher-order (epistatic) variance components to 0 (Cordell et al. 1995), which fits an additive model on the penetrance scale to the effects at the m unlinked loci. This model is a good approximation of a model of genetic heterogeneity (Risch 1990_a_), which biologically implies that the loci act via separate etiologic pathways to cause the disease. Alternatively, by expressing the epistatic components in terms of the first-order variance components, we can fit the multiplicative epistatic model defined by Risch (1990_a_). Note that, for unlinked loci, the MLS for a multiplicative model will equal the sum of the individual single-locus MLS values and, therefore, will give no increased power to detect an effect.
in (2), may be written in terms of the prior probabilities f i_1_i_2…_i m j and the 3_m_-1 underlying additive and dominance variances caused by the m disease-causing loci (divided by a constant). The MLS may therefore be written in terms of the variance components (divided by a constant) and the prior and posterior probabilities of the IBD sharing at the m loci. For all relatives, these probabilities can be calculated at increments across the genome, by use of the inheritance-vector distribution (Kruglyak et al. 1996). By maximizing the likelihood with respect to the variance component parameters, rather than with respect to the z i_1_i_2…_i m j, we may fit specific classes of genetic models to the data—for example, single-locus models, two-locus models, three-locus models, etc. Note that the “possible triangle” restrictions on the _z_s (Holmans 1993) will automatically be satisfied by restriction of the variance components to nonnegative quantities. When more than one disease locus is considered, we may set the second- or higher-order (epistatic) variance components to 0 (Cordell et al. 1995), which fits an additive model on the penetrance scale to the effects at the m unlinked loci. This model is a good approximation of a model of genetic heterogeneity (Risch 1990_a_), which biologically implies that the loci act via separate etiologic pathways to cause the disease. Alternatively, by expressing the epistatic components in terms of the first-order variance components, we can fit the multiplicative epistatic model defined by Risch (1990_a_). Note that, for unlinked loci, the MLS for a multiplicative model will equal the sum of the individual single-locus MLS values and, therefore, will give no increased power to detect an effect.
The additional evidence for linkage at a locus, conditional on linkage at _m_-1 previous loci, can be assessed by the difference in MLS between the best-fitting _m_-1 locus model and the model with an _m_th locus included (Cordell et al. 1995). We can calculate MLS curves across the genome, for a series of nested models, by looking first for evidence of a single disease locus, then by conditioning on a first locus at a given position and looking for evidence at a second disease locus, and then by conditioning on two loci at given locations and looking for evidence at a third disease locus, and so on. Alternatively, we could start by conditioning on effects at previously identified loci. Although this procedure could theoretically be continued for an arbitrary number of loci, the amount of data available and the increased degrees of freedom for the m locus models will limit the number of loci that can be modeled simultaneously; for data sets of the size currently available, it may not be useful for more than ∼3 disease loci. However, by fitting a restricted model such as the previously described additive model, the degrees of freedom can be significantly reduced, and larger numbers of disease loci could be considered simultaneously.
Results
The methods described above were applied to simulated and to real data. We generated IBD probabilities by use of the program GENIBD (S.A.G.E. 1998), which has the advantages of being significantly faster than the GENEHUNTER program of Kruglyak et al. (1996) and of allowing for a slightly larger maximum family size. We used a yet-to-be released version of GENIBD that also allows the calculation of joint IBD probabilities at linked loci.
Application to Simulated Data
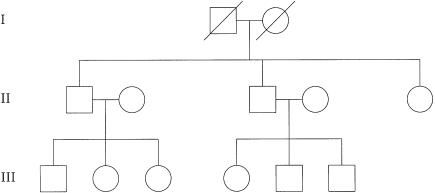
We simulated data for 25 families with the pedigree structure shown in figure 1. This structure is identical to that simulated by Kruglyak et al (1996). Marker data were simulated at 11 markers spaced at 10-cM intervals on each of four chromosomes, under the assumption that each marker had five equifrequent alleles. The disease was assumed to be caused by a three-locus model, with three disease loci—A, B, and C—lying in the centers of chromosomes 1, 2, and 3. The population prevalence of each disease allele was .05, and the penetrance of each three-locus genotype was 1 for individuals who possessed two disease alleles at any of the three disease loci and was 0 otherwise. Families were included in the study if they had at least three affected members in generation III, with at least one affected individual in each generation III sibship. Individuals in generation I were assumed to be unavailable for genotyping.
Figure 1.
Structure of pedigrees used for the simulation study. Families were included in the study if they had at least three affected members in generation III, including at least one affected individual in each sibship. Individuals in generation I were assumed to be unavailable for genotyping.
Significance levels for MLS values obtained in a data set were calculated by simulation and analysis of sets of marker data across a chromosome for an identical data set (in terms of structure of families and disease status of individuals). The alleles across a chromosome were dropped at random through the given families (allowing for intermarker recombination by use of the Haldane mapping function), and, for testing of a single-locus model, the distribution of the resulting MLS at any given location was calculated. For testing of an _m_th locus unlinked to a set of previous _m_-1 loci, a similar procedure can be followed, but the marker data in the regions of the _m_-1 loci must be fixed at their original observed values. This procedure will not be valid if the _m_th locus is linked to any of the previous _m_-1, although consideration of the distribution of the MLS in this case (Farrall 1997) suggests that this procedure will then give conservative significance levels. By examination of the distribution of the resulting multipoint MLSs at a single location, approximate data-specific pointwise (as opposed to genomewide) P values can be found. Note that the significance levels will be data-set specific because of the correlation between the affected relative pairs, and, hence, simulation will be needed to generate the P values, unless only independent pairs are used.
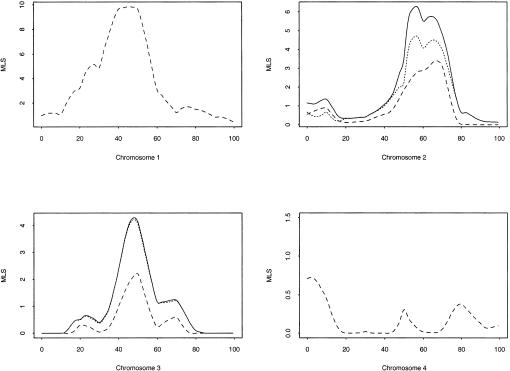
The MLS results for a single simulated replicate are shown in figure 2. Although analysis of a single replicate does not allow us to make a global inference about power, it is useful in terms of illustrating the kind of results we might expect to find in an analysis of real data. We see that locus A is easily identified, with an MLS of 9.8 (P<.001) in the correct location, but that locus B is less significant, with an MLS of 1.8 (_P_=.02) at the correct location or of 3.4 (_P_≈.002) at a distance of 16 cM away. Locus C is also less significant, with an MLS of 2.2 (_P_=.01) at the correct location. Figure 2 also shows, for chromosomes 2 and 3, the improvement in MLS when a two-locus analysis is performed, conditioning on the result for locus A on chromosome 1. We see that the additive and general two-locus analyses give a big improvement, compared with the single-locus analysis, in terms of locating the second disease locus both more accurately and with greater significance, giving an additive MLS of 4.7 (P<.001) or a general MLS of 6.3 (P<.001) close to locus B and an additive MLS of 4.2 (P<.001) or a general MLS of 4.3 (_P_≈.003) at locus C. We also used a three-locus model to analyze the data for chromosome 3, given the results at loci A and B, but no further improvement in significance was found, compared with the two-locus model.
Figure 2.
Single-locus and two-locus MLS results against chromosomal location (in cM), for data simulated under a three-locus recessive model. Dotted lines indicate additive MLS; dashed lines, multiplicative or single-locus MLS; and solid lines, general MLS.
To investigate the power of the multilocus strategy in a larger number of replicates, we simulated 100 replicates of the three-locus model described above. Since calculation of P values in the extreme tail of the distribution would be prohibitively time consuming, we simulated only 10 sets of families—rather than 25 families—per replicate, to generate more-modest significance levels. We found that the additive or general MLS for locus B, conditional on locus A, was more significant than the single-locus (or multiplicative) MLS for locus B alone, in 56% of replicates. Specifically, the power to detect locus B (with _P_=.05) was 57% for the additive MLS and 56% for the general MLS, compared with 51% for the single-locus or multiplicative MLS, illustrating a small increase in power when the multilocus method was used. Results were similar for locus C (as expected by symmetry).
We simulated two further three-locus models in which the effect at locus A was large, compared with the effects at loci B and C. This might be expected to more closely resemble the situation in type 1 diabetes (see analysis of real data below), in which there is a single major genetic component (the locus IDDM1 in the HLA region on chromosome 6p21) but in which there is also a large number of smaller effects at other loci. The models were identical to that described previously, except that, in the first, or symmetric (in loci B and C), model, the penetrance of each three-locus genotype was 1 for individuals with two disease alleles at A and .25 for individuals with two disease alleles at locus B or C. In the second, or asymmetric, model the penetrance of each three-locus genotype was 1 for individuals with two disease alleles at locus A, .5 for individuals with two disease alleles at locus B, and .25 for individuals with two disease alleles at locus C. For the symmetric model, we found that the additive or general MLS for locus B, conditional on locus A, was more significant than the single-locus (or multiplicative) MLS for locus B alone, in 69% of replicates, with a power to detect an effect (with _P_=.05) that was 13% for the additive model and 8% for the general model, compared with 7% for the single-locus model. For the asymmetric model, we found that the additive or general MLS for locus B, conditional on locus A, was more significant than the single-locus (or multiplicative) MLS for locus B alone, in 70% of replicates, with a power to detect an effect (with _P_=.05) that was 31% for the additive model and 27% for the general model, compared with 19% for the single-locus model.
Application to Real Data for Type 1 Diabetes
We also analyzed real data from a second genome screen (Mein et al. 1998) of 356 ASPs (with genotyped parents) affected with type 1 diabetes. Type 1 diabetes, or insulin-dependent diabetes mellitus (IDDM), is a complex trait with a number of genetic and environmental determinants. The major genetic component is the locus IDDM1 in the HLA region on chromosome 6p21, but a large number of smaller effects at other loci have also been identified (Davies et al. 1994). Since IDDM1 plays such an important role in the disease, it is of interest to examine the effects at other loci after the effect of IDDM1 has been taken into account. This has been done for IDDM2 and IDDM4, by use of two-locus MLS methods (Cordell et al 1995), and, more crudely, in other regions of the genome, by subdivision of the data according to HLA sharing status, genotype, or alleles present (Davies et al. 1994; Mein et al. 1998; Cucca et al. 1998_a_). Here we use our previously described stepwise strategy.
Table 1 shows all locations in the genome with an MLS > 1.4 (_P_=.01), as obtained by use of a single-locus analysis. Table 1 also includes locations that were not significant in the single-locus analysis but that were interesting in light of subsequent multilocus analyses. The most-significant MLS is at IDDM1. For the two-locus analysis, we therefore fix IDDM1 as the first disease locus and consider the joint IBD sharing at IDDM1 and at a second locus, which is placed at 1-cM intervals across the genome. MLS curves were fitted under multiplicative, additive, and general genetic models, for the action of the two loci; the MLS for the action of IDDM1 was subtracted so that the curves represent the additional effect of locus 2 and, for multiplicative and general models, its epistatic interactions (Cordell et al. 1995). We call these MLS values “conditional MLS values,” since the statistics are conditional on the previously identified effect at IDDM1.
Table 1.
Maximum and Conditional MLS Values (with P Values) for Selected Chromosomes[Note]
| MLS (P) | |||||
|---|---|---|---|---|---|
| Chromosome | Closest Marker (or IDDM locus) | Location on Fig. 3 (cM) | Single Locusa | Two Locus Conditional | Three Locus Conditional |
| 3 | D3S1576 | … | 1.01 (.03) | 1.28 (.04) | 2.88 (.004) |
| 6 | D6S291 (IDDM1) | 29 | 34.7 (HS) | … (…) | … (…) |
| 6 | D6S294-D6S286 | 56 | 19.4 (HS) | 2.42b (.001) | 2.60 (.008) |
| 8 | D8S88 | 111 | .70 (NS) | 1.62 (.03) | 2.25 (.01) |
| 10 | D10S220 (IDDM10) | 51 | 4.67 (.000004) | 5.02 (.000008) | … (…) |
| 11 | TH/INS (IDDM2) | 3 | 2.77 (.0003) | 4.14 (.00006) | 5.17 (.0002) |
| 11 | FGF3 (IDDM4) | 81 | .54 (NS) | 2.04b (.002) | 1.97b (.003) |
| 14 | D14S75-D14S276 | … | 1.95 (.002) | 2.42 (.003) | 2.83 (.004) |
| 15 | CYP19-D15S125 | 39–57 | .74 (.05) | 1.12b (.02) | 1.72b (.005) |
| 16 | D16S3098 | 87 | 3.24 (.0001) | 4.92 (.00001) | 5.02 (.0002) |
| 18 | D18S487 | 72 | 1.10 (.02) | 1.95b (.002) | 1.98b (.003) |
| 19 | D19S226 | … | 1.80 (.004) | 1.96 (.02) | 2.18 (.02) |
| 21 | D21S120 | 5 | .06 (NS) | .95 (.07) | 1.59 (.04) |
| Pseudoautosomal | DXYS154 | 33 | 1.23 (.02) | 1.65b (.005) | 1.12b (.02) |
As expected, at positions unlinked to IDDM1, the multiplicative curves were identical to those curves obtained by use of a single-locus model (data not shown) for locus 2. The P values for these conditional multiplicative MLS values will therefore be identical to those given by Holmans (1993) for the single-locus “possible triangle” method. Since each family contains exactly two affected sibs, no correction for nonindependence of the pairs is required. The additive model has the same number of free parameters (two for each locus) as does the multiplicative model; therefore, the distribution of the test statistic for the additive model should be similar to that of the single-locus MLS, as has indeed been observed in simulations for a variety of specific additive models (Cordell et al. 1995; Farrall 1997). The distribution of the general two-locus MLS is somewhat different, since there are eight free parameters when the effect of both loci is tested and six free parameters when the effect of locus 2, given locus 1, is tested. Imposition of the “possible triangle” constraints means that the distribution cannot be calculated by use of standard asymptotic theory; we therefore used simulation to calculate the two-locus P values via importance sampling (Hammersley and Handscombe 1964; Kong et al. 1992), as described in Cordell et al. (1995).
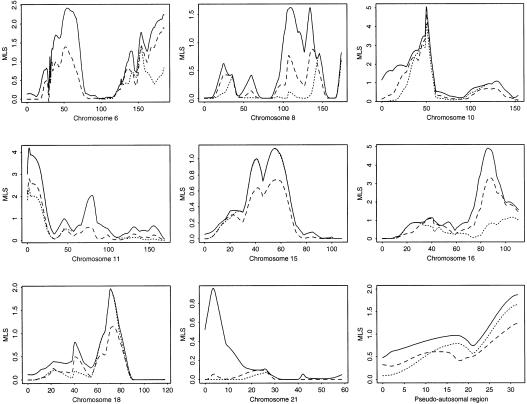
Figure 3 and the Two Locus Conditional column of table 1 show the most important results. Parameter estimates for the significant two-locus models are given in table 2. Chromosome 6 is particularly interesting, since we see evidence for an additional susceptibility locus in the D6S294_–_D5S286 region, ∼20 cM from IDDM1, with an additive maximum MLS of 2.42 (_P_=.001), which is considerably more significant than the multiplicative MLS of 1.39 (_P_=.01) at this location. The position of the peak identified in this analysis lies between IDDM1 and the putative peak for IDDM15 (Delépine et al. 1997), ∼25 cM from IDDM15. The two-locus analysis is particularly useful in this region, since, with use of a single-locus method, any effects tend to be masked by the highly significant effect at IDDM1 (e.g., the single-locus MLS, not accounting for IDDM1, is 19.4 at this location). The parameter estimates in table 2 indicate that, although IDDM1 makes a greater contribution to the overall genetic variance, there are nonnegligible effects caused by the second locus. On this chromosome, we also find some evidence for a third locus on the other arm, near D6S271, which may correspond to IDDM8 (Luo et al. 1995); however, in this case, the two-locus conditional analysis does not offer any improvement in MLS, compared with single-locus analysis.
Figure 3.
Two-locus MLS results (conditional on IDDM1) for IDDM data against chromosomal location in cM for chromosomes 6, 8, 10, 11, 15, 16, 18, and 21 and for the pseudo autosomal region. Dotted lines indicate additive MLS, solid lines indicate general MLS, and dashed lines indicate multiplicative or single-locus MLS (apart from chromosome 6, where dashed lines indicate multiplicative MLS only).
Table 2.
Parameter Estimates for Two-Locus Models (Conditional on IDDM1) for Selected Loci[Note]
| Closest Marker Locus | ||||||||
|---|---|---|---|---|---|---|---|---|
| Parametera | D6S294b | D8S88 | D10S220 | TH/INS | FGF3b | D16S3098 | D18S487b | DXYS154b |
| V _A_1/(_K_2) | 2.639 | 1.508 | 3.622 | .000 | 2.155 | 1.652 | 1.749 | 3.742 |
| V _A_2/(_K_2) | 4.345 | .000 | 2.822 | .000 | .324 | .221 | .000 | 2.686 |
| V _D_1/(_K_2) | 7.363 | 2.708 | 6.097 | 3.885 | 5.305 | .424 | 4.547 | 8.391 |
| V _D_2/(_K_2) | .212 | .000 | .000 | .194 | 1.104 | .000 | 1.092 | .000 |
| V _A_1_A_2/(_K_2) | .000 | .000 | .000 | 2.735 | .000 | .000 | .000 | .000 |
| V _A_1_D_2/(_K_2) | .000 | .000 | 1.347 | .362 | .000 | .000 | .000 | .000 |
| V _A_2_D_1/(_K_2) | .000 | .000 | 5.286 | .000 | .000 | 7.165 | .000 | .000 |
| V _D_1_D_2/(_K_2) | .000 | 3.445 | .000 | .000 | .000 | .000 | .000 | .000 |
| _z_00 | .020 | .024 | .010 | .023 | .016 | .021 | .019 | .010 |
| _z_01 | .051 | .472 | .046 | .045 | .038 | .047 | .038 | .046 |
| _z_02 | .018 | .024 | .036 | .027 | .039 | .026 | .040 | .037 |
| _z_10 | .037 | .083 | .053 | .045 | .068 | .078 | .071 | .057 |
| _z_11 | .207 | .166 | .161 | .153 | .146 | .165 | .143 | .167 |
| _z_12 | .111 | .083 | .120 | .125 | .114 | .087 | .113 | .110 |
| _z_20 | .036 | .123 | .102 | .111 | .138 | .065 | .139 | .130 |
| _z_21 | .212 | .246 | .281 | .284 | .281 | .288 | .278 | .287 |
| _z_22 | .307 | .205 | .192 | .186 | .161 | .223 | .160 | .157 |
Chromosome 10 has the most-significant MLS outside the HLA region, both in single- and two-locus analysis, but the two-locus conditional result does not give increased significance, compared with the single-locus analysis. This locus has been previously designated as “IDDM10” (Reed et al. 1997; Mein et al. 1998). For chromosome 11, at IDDM2 we see a significant improvement in conditional MLS, an improvement from 2.77 for a single-locus or multiplicative model to 4.14 for a general model. No improvement is found when an additive model is used. These results are similar to those of Cordell et al. (1995), who found that epistatic components of variance were required to model the joint action of IDDM1 and IDDM2, although our results here differ from theirs in that they suggest that epistatic terms which are more general than multiplicative terms are required. From table 2, we see that the data are well modeled by a large dominance effect at locus 1, together with a large additive × additive epistatic effect plus some smaller effects. By splitting according to HLA status, only a modest improvement in MLS is found among 0 or 1 sharers, indicating that our approach here may be more powerful for detection of these types of effects. Still considering chromosome 11, at IDDM4 we see a significant increase in MLS, an increase from 0.54 for a single-locus model to 2.04 for an additive or general two-locus model. This finding is consistent with the results of Cordell et al. (1995), who showed that IDDM1 and IDDM4 act additively to cause type 1 diabetes (however, these results are not completely independent, because these two studies have 93 families in common). A similar result is seen by splitting the data and by analyzing only HLA 0 or 1 sharers, as might be expected from the estimates of the sharing parameters z ij in table 2, which show deviation from expected proportions when _i_=0 or _i_=1 but not when _i_=2.
On chromosome 16, we find another significant effect that is increased when a general two-locus model, rather than a single-locus model, is fitted. No improvement in significance is observed when an additive model is fitted; indeed, a decrease in seen. Splitting according to HLA status gives only a modest improvement among 0 or 1 sharers, as might be expected from the estimates of the sharing parameters z ij, in which little deviation in expected sharing is seen for _i_=0 or _i_=1. This again indicates the greater power of a multilocus strategy. For chromosome 8, we see a maximum conditional MLS of 1.62 for the general model, which is 0.9 units larger than the single-locus MLS. The additive model gives no improvement in MLS. These results are consistent with those of Mein et al. (1998), who obtained, on chromosome 8, a similar increase in significance among ASPs that share 2 HLA alleles IBD but who saw no increase among ASPs that share 0 or 1 HLA alleles IBD; see also Cucca et al. (1998_b_). On chromosome 18, we find a significant increase in MLS, an increase from 1.10 for a single-locus model to 1.95 for a two-locus model, whereas splitting by HLA status gives no increased significance. On chromosome 21, we find a locus of modest significance when a two-locus model is used, which is similar to the result seen among pairs sharing 2 HLA alleles IBD. Finally, in the pseudoautosomal region of the sex chromosomes, we find an increase in MLS, an increase from 1.23 for a single-locus model to 1.65 for an additive and 1.87 for a general two-locus model.
Since the most-significant result for a second locus is seen at IDDM10, we used our methods to screen for a third locus, conditioning on the sharing at IDDM1 and IDDM10. The calculated MLS values correspond to the differences in MLS between the three-locus and the two-locus model for IDDM1 and IDDM10, under three different genetic models: multiplicative, additive, and general (which includes all 27 components of variance). The P values were calculated by simulation of data under the null hypothesis that only IDDM1 and IDDM10 have an impact on the IBD sharing between affected sibs, by use of 10,000 simulated replicates. Results are shown in the Three Locus Conditional column of table 1. The results for chromosomes 3, 8, 15, and 21 are of particular interest, since the three-locus method gives more significant results than either the single-locus or two-locus methods, illustrating again the greater power of the multilocus approach. We also conducted four-locus analyses, assuming an additive model for the action of a hypothetical fourth disease locus, given the effects at IDDM1, IDDM10, and IDDM2, but we found no increase in significance, compared with single-, two-, or three-locus models.
Discussion
A variety of model-free methods for testing linkage for complex diseases currently exists. The common feature of most of these methods is that they measure, at different locations on the genome, the observed IBD sharing between pairs or groups of relatives and that they compare this with the expected sharing under the null hypothesis of no linkage to disease. Within this broad class of methods, the likelihood-based statistic proposed in the present study has the advantage of providing a natural statistic for pairwise IBD sharing that may easily be extended to account for multilocus disease models. This approach has been shown, in the present study and elsewhere (Cordell et al. 1995, 1999), to give increased power for detection of any one of the disease loci in certain circumstances, which will depend heavily on the true underlying multilocus model. For the data on type 1 diabetes analyzed here, conditioning on the large effect at IDDM1, via a two-locus model, allowed the detection of several effects that had not been apparent from single-locus analyses. In table 2, examination of the estimates of the sharing parameters z ij shows that, for some loci, the deviation from expected sharing occurred in such a way that subdividing the data according to HLA sharing status and performing a single-locus analysis would be expected to produce the same results as would the two-locus analysis. For other loci, this procedure would be unlikely to be useful. Although examination of the maximum-likelihood estimates of the sharing parameters can be informative, we must beware of overinterpretation of the estimates of the variance component parameters, since they merely provide a means of modeling the sharing parameters, under the assumption of an m locus model of disease. For a complex disease in which there are likely to be many loci involved, it is not clear to what extent the parameter estimates generated under the assumption of a two-locus—or even a three-locus—disease model will resemble their true population quantities.
A possible disadvantage of the statistic presented in (2) is that it considers only pairs of affected relatives, as opposed to considering IBD sharing among a larger set. Kruglyak et al. (1996) suggest that this may result in a loss in power, since, in their simulations with GENEHUNTER, the statistic NPLall performed better than did the statistic NPLpairs in most cases. However, Kong and Cox (1997) found that, for their modified NPL statistic, the choice of scoring function (with the use of affected pairs or all affected individuals) did not make much difference in their final results. Although allele sharing among large sets of affected relatives may be more informative than sharing among pairs only, the decrease in power for our statistic is likely to be outweighed by the increase in power gained by being able to simultaneously consider and model the action of several disease loci.
The likelihood-based statistic (2) implicitly assumes that all affected pairs are independent, which will not be the case for data from extended pedigrees or, indeed, from sibships of size >2. In our own simulations of large sibships, we found a negligible increase in type 1 errors when we assumed independence and used equal weights, which is consistent with the results of Meunier et al. (1997) and Greenwood and Bull (1999). For extended family data, however, the effect of the nonindependence may be much greater, depending on the family size and the relationships involved. It is therefore important, when using data from nonindependent pairs, that the significance levels be calculated by use of simulation, as previously described.
In addition to testing the hypothesis of linkage at a given location, conditional on linkages at previous locations, the multilocus models described in the present study may be used to test the fit of specific biological models (Cordell et al. 1995), by consideration of the difference in MLS between a restricted (e.g., additive or multiplicative) model and the general model. Again, the significance of the difference in MLS must be evaluated by simulation; an intuitive method for doing this would be to simulate from the best-fitting additive or multiplicative model, to see whether the increase in MLS for a general model is significantly large. This means that simulation of IBD sharing among pairs of affected relatives must be done using the maximum-likelihood IBD-sharing probabilities for the additive or multiplicative model as the “true” values. This will only be valid if the pairs of affected relatives are in fact independent. For the previously described IDDM data, we have exactly one ASP per family, and, therefore, the independence assumption is justified. We estimated P values by simulation, under the additional assumption that all markers were fully informative, which greatly simplifies the simulations (which then need only be performed at a single marker). The results of Holmans (1993) suggest that this should not make too much difference to the significance criteria obtained. Using this approach, we found that, for IDDM1 and IDDM2, there is some evidence against the null hypothesis that these two loci act multiplicatively (difference in _MLS_=1.38, _P_=.04) and against the null hypothesis that the two loci act additively (difference in _MLS_=1.77, _P_=.01). For IDDM1 and IDDM4, there is evidence against multiplicativity (difference in _MLS_=1.49, _P_=.008), but there is no evidence against additivity (difference in _MLS_=0). For IDDM1 and chromosome 16, there is evidence against multiplicativity (difference in _MLS_=1.68, _P_=.02), and there is strong evidence against additivity (difference in _MLS_=4.16, P<.0001). For IDDM1 and IDDM10, there is no evidence against multiplicativity (difference in _MLS_=0.36, _P_=.58), but there is some evidence against additivity (difference in _MLS_=0.87, _P_=.05).
Use of simulation to determine significance levels, rather than relying on some asymptotic distribution, may seem rather cumbersome. However, even methods for which a normal approximation is available may require simulation to evaluate significance levels, unless the number of families is large (Kong and Cox 1997). An alternative randomization method for calculation of significance thresholds, which is especially useful when parental marker data are not available, has been proposed by Zhao et al. (1999). Although it is important to set some criteria for significance, it is perhaps more important, particularly for complex diseases, simply to gain an idea of the general pattern of results. This can provide a starting point in terms of determining which regions of the genome are more or less promising for further investigation. On this note, it is interesting to observe that, in most cases, we find the general pattern for the single-locus MLS results to be similar to that of the NPL statistic of Kong and Cox (1997) but with the MLS approach having the advantage of being easily extended to the multilocus case.
Software for calculation of single-, two-, and three-locus MLS values, given the prior and posterior IBD-sharing probabilities, is available from the corresponding author of the present article. Software for calculation of the prior and posterior IBD-sharing probabilities is available in a number of statistical genetics packages, including GENIBD of S.A.G.E., which was used for the analyses presented here.
Acknowledgment
This work was supported in part by U.S. Public Health Service grant GM28356 from the National Institute of General Medical Sciences. Some of the results of this paper were obtained by use of S.A.G.E., which is supported by U.S. Public Health Service Resource grant 1 P41 RR03655 from the National Center for Research Resources. We thank Charles Mein and John Todd’s group, for sharing their family data for type 1 diabetes.
Appendix
Here we show that the z i_1_i_2…_i m j may be written in terms of the prior probabilities f i_1_i_2…_i m j and 3_m_-1 underlying additive and dominance variances (divided by a constant) caused by the m disease-causing loci.
For a relative pair j of type R, the z i_1_i_2…_i m j may be written (Cordell at al. 1995) as
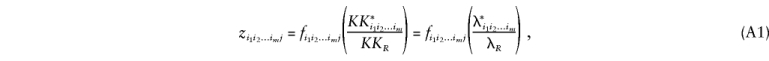
where K is the population prevalence of the disease, K R is the risk to relatives of type R of an affected individual, λ_R_ is the risk ratio or relative risk K R/K, and K*i_1_i_2…_i m and λ*i_1_i_2…_i m are the prevalence and risk ratio for a relative who shares (_i_1,i_2,…,i m) alleles IBD with an affected individual at loci 1,2…,m. Now λ_R may be written (James 1971)
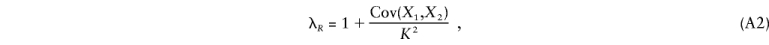
where Cov denotes covariance, X i is the phenotype of person i (_i_=1,2)—defined to be 0 or 1, according to whether the person is unaffected or affected—and person 2 is a type R relative of person 1.
If the disease is caused by a single disease locus, we may write (Kempthorne 1957; James 1971; Risch 1990_a_) Cov(_X_1,X_2)=2_r R V A+u R V D, where V A and V D are the additive and dominance variances caused by the disease locus, where r R is the kinship coefficient or coefficient of coancestry (the probability that a random allele from individual 1 is IBD with a random allele from the same locus in individual 2) and where u R is the coefficient of fraternity (Trustrum 1961) or the probability that two alleles are shared IBD, at a locus, by the individuals. We may express r R and u R in terms of the (prior) probabilities of the relative pair sharing 0, 1, and 2 alleles IBD as r _R_=0.5_f_2+0.25_f_1 and u _R_=f_2. Recalling that λ*0, λ*1, and λ*2 will be equivalent to the relative risks for an unrelated individual, an offspring, and a monozygotic twin of an affected individual, respectively, we can therefore express λ*i_1_i_2…_i m and λ_R and, thus, equation (A1), in terms of the parameters V A/(_K_2) and V D/(_K_2).
If the disease is caused by effects at two disease loci, we follow a similar procedure to express λ*i_1_i_2…_i m and λ_R_ in terms of V A k and V D k (the additive and dominance variances caused by locus k) and V _A_1_A_2, V _A_1_D_2, V _A_2_D_1, and V _D_1_D_2, the additive × additive, additive × dominance, dominance × additive, and dominance × dominance variances caused by loci 1 and 2, respectively (Kempthorne 1957). Cordell et al. (1995) give formulae for the λ*_i_1_i_2 (_i_1,_i_2=0,1,2) in terms of these eight variance components and K, the population prevalence. These formulae apply, regardless of whether the two disease loci are linked, because the λ*_i_1_i_2 are conditional on sharing _i_1 alleles IBD at locus 1 and i_2 at locus 2, so that any linkage information is irrelevant. All that remains is to derive expressions for λ_R in terms of these same components. These have previously been derived for siblings by Cordell et al. (1995), under the assumption of there being two unlinked disease loci, and they have been extended to the case in which the loci are linked by Farrall (1997). More generally, for any relationship, we may write
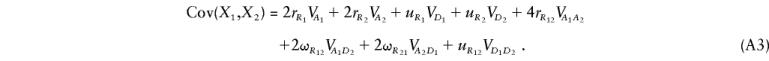
Here, r R k and u R k are, respectively, the kinship coefficient and coefficient of fraternity for locus k. The terms r _R_12, ω_R_12, ω_R_21, and u _R_12 are more difficult to define but come from the generalization of the formula for unlinked loci (Kempthorne 1957; Cordell et al. 1995; Lynch and Walsh 1998). For unlinked loci, we can express the coefficients as the product of the coefficients for the single-locus terms—that is, r _R_12=r R_1_r _R_2, ω_R_12=r R_1_u _R_2, ω_R_21=r R_2_u _R_1, and u _R_12=u R_1_u _R_2. For arbitrary linkage between the loci, we must define r _R_12 as the simultaneous probability that a randomly chosen allele at locus 1 in individual 1 is IBD with a randomly chosen allele at locus 1 in individual 2 and that a randomly chosen allele at locus 2 in individual 1 is IBD with a randomly chosen allele at locus 2 in individual 2. Similarly, ω_R_12 is the probability that a randomly chosen allele at locus 1 in individual 1 is IBD with a randomly chosen allele at locus 1 in individual 2 and that 2 alleles are shared IBD by the individuals at locus 2, and so on for ω_R_21 and u _R_12. The coefficients in equation (A3) may therefore be written as
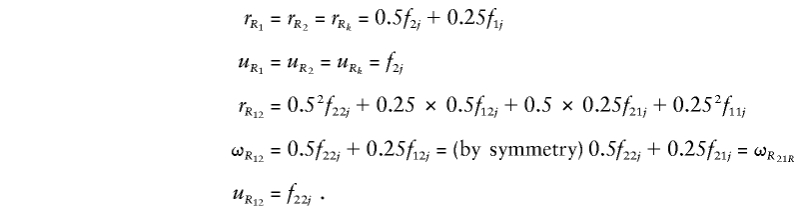
By inserting the above expressions into equations (A3), (A2), and (A1), we may therefore parameterize z i_1_i_2…_i m j in terms of the eight variance components divided by _K_2.
For an arbitrary number m of disease loci, we proceed in a similar fashion. Let V A S D T be the covariance term for an effect that involves additive effects in a specific set S of s loci and dominance effects in a specific set T of t loci (i.e., set S is of size s; set T is of size t). We have the general formula (Kempthorne 1957; Cordell et al. 1995)
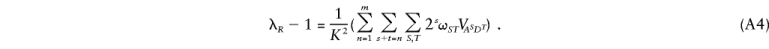
If the loci are all unlinked, the coefficients ω_ST_ can be written as a_∈_Sr R a b_∈_Tu R b_=(r R)s(u R)t, where r R and u R are the kinship coefficient and coefficient of fraternity for the relative pair and where r R a and u R a are the locus-specific kinship coefficient and coefficient of fraternity at a locus a, defined, respectively, as the probability that a randomly chosen allele at locus a in individual 1 is IBD with a randomly chosen allele at locus a in individual 2 and the probability that the two alleles at locus a in individual 1 are IBD with the two alleles at locus a in individual 2. More generally, if any among the loci are linked, the coefficients ω_ST can be written as ω_ST_=ω_a_1_a_2…a s,b_1_b_2…_b t, which is defined as the simultaneous probability that, at all of the loci _a_1,a_2…_a s, a randomly chosen allele in individual 1 is IBD with a randomly chosen allele in individual 2, and that, at all of loci _b_1,b_2…_b t, the individuals share two alleles IBD. As for two disease loci, these coefficients can be written in terms of the prior probabilities f i_1_i_2…_i m j, which will depend on the recombination fractions between any of the loci. It is helpful to illustrate this for the case of three disease loci. In that case, we have
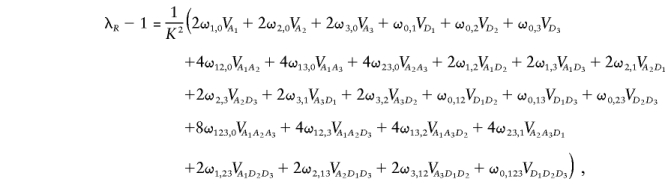
where

and where f i(a) is the (prior) probability of the pair sharing i alleles IBD at locus a, where f ij(ab) is the (prior) probability of the pair sharing i alleles IBD at locus a and j alleles IBD at locus b, where f ijk(abc) is the (prior) probability of the pair sharing i alleles IBD at locus a, j alleles IBD at locus b and k alleles IBD at locus c, and so on.
We have now expressed λ_R_ in terms of 3_m_-1 variance components divided by K_2. We can use the reasoning of Cordell et al. (1995) and can apply it to equation (A4) to argue that λ*i_1_i_2…_i m can be expressed in the same way as λ_R but with coefficients that correspond to the product of the locus-specific coefficients for the sharing at each locus. In the case of three disease loci, this gives the following expression for λ*_i_1_i_2_i_3:
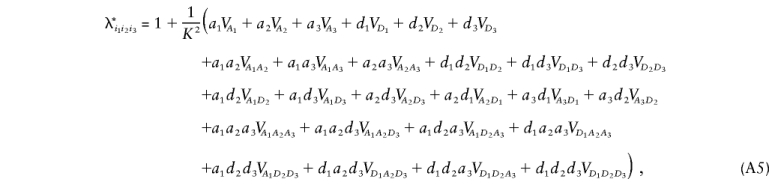
where a k takes the value 0 if i _k_=0, 0.5 if i _k_=1, and 1 if i _k_=2 and where d k takes the value 0 if i _k_=0, 0 if i _k_=1, and 1 if i _k_=2.
References
- Cordell HJ, Todd JA, Bennett ST, Kawaguchi Y, Farrall M (1995) Two-locus maximum LOD score analysis of a multifactorial trait: joint consideration of IDDM2 and IDDM4 with IDDM1 in type 1 diabetes. Am J Hum Genet 57:920–934 [PMC free article] [PubMed]
- Cordell HJ, Jacobs KB, Wedig GC, Elston RC (1999) Improving the power for disease locus detection in affected-sib-pair studies by using two-locus analysis and multiple regression methods. Genet Epidemiol 17 Suppl 1:S521–526 [DOI] [PubMed] [Google Scholar]
- Cox NJ, Xu J, Beaty TH, Blumenthal M, Ober C, Bleecker ER, Friedhoff L, et al (1998) Using evidence for interactions to identify regions containing asthma susceptibility loci. Am J Hum Genet 63(Suppl):A286 [Google Scholar]
- Cox NJ, Frigge M, Nicolae DL, Concannon P, Hanis CL, Bell GI and Kong A (1999) Loci on chromosomes 2 (NIDDM1) and 15 interact to increase susceptibility to diabetes in Mexican Americans. Nat Genet 21:213–215 [DOI] [PubMed]
- Cucca F, Esposito L, Goy JV, Merriman ME, Wilson AJ, Reed PW, Bain SC, et al (1998_a_) Investigation of linkage of chromosome 8 to type 1 diabetes: multipoint analysis and exclusion mapping of human chromosome 8 in 593 affected sib-pair families from the U.K. and U.S. Diabetes 47:1525–1527 [DOI] [PubMed]
- Cucca F, Goy JV, Kawaguchi Y, Esposito L, Merriman ME, Wilson AJ, Cordell HJ, et al. (1998_b_) A male-female bias in type 1 diabetes and linkage to chromosome Xp in MHC HLA-DR3-positive patients. Nat Genet 19:301–302 [DOI] [PubMed]
- Davies JL, Kawaguchi Y, Bennett ST, Copeman JB, Cordell HJ, Pritchard LE, Reed PW, et al (1994) A genome-wide search for human type 1 diabetes susceptibility genes. Nature 371:130–136 [DOI] [PubMed]
- Delépine M, Pociot F, Habita C, Hashimoto L, Froguel P, Rotter J, Cambon-Thomsen A, et al (1997) Evidence of a non-MHC susceptibility locus in type 1 diabetes linked to HLA on chromosome 6. Am J Hum Genet 60:174–187 [PMC free article] [PubMed]
- Dizier MH, Babron MC, Clerget-Darpoux F (1994) Interactive effect of two candidate genes in a disease: extension of the marker-association-segregation χ2 method. Am J Hum Genet 55:1042–1049 [PMC free article] [PubMed]
- Dizier MH, Clerget-Darpoux F (1986) Two disease locus model: sib pair method using information on both HLA and Gm. Genet Epidemiol 3:343–356 [DOI] [PubMed] [Google Scholar]
- Dupuis J, Brown O, Siegmund D (1995) Statistical methods for linkage analysis of complex traits of complex traits from high-resolution maps of identity by descent. Genetics 140:843–856 [DOI] [PMC free article] [PubMed]
- Elston RC (1995) The genetic dissection of multifactorial traits. Clin Exp Allergy 25(Suppl 2):103–106 [DOI] [PubMed] [Google Scholar]
- ——— (1998) Methods of linkage analysis—and the assumptions underlying them. Am J Hum Genet 63:931–934 [DOI] [PMC free article] [PubMed]
- Farrall M (1997) Affected sibpair linkage tests for multiple linked susceptibility genes. Genet Epidemiol 14:103–115 [DOI] [PubMed] [Google Scholar]
- Greenwood CMT, Bull SB (1999) Down-weighting of multiple affected sib pairs leads to biased likelihood-ratio tests, under the assumption of no linkage. Am J Hum Genet 64:1248–1252 [DOI] [PMC free article] [PubMed]
- Hammersley JM, Handscomb DC (1964) Monte Carlo methods. Chapman & Hall, New York [Google Scholar]
- Holmans P (1993) Asymptotic properties of affected-sib-pair linkage analysis. Am J Hum Genet 52:362–374 [PMC free article] [PubMed]
- James JW (1971) Frequency in relatives for an all-or-none trait. Ann Hum Genet 35: 47–48 [DOI] [PubMed]
- Kempthorne O (1957) An introduction to genetic statistics. John Wiley & Sons, New York [Google Scholar]
- Knapp M, Seuchter SA, Baur MP (1994) Two-locus disease models with two marker loci: the power of affected-sib-pair tests. Am J Hum Genet 55:1030–1041 [PMC free article] [PubMed]
- Kong A, Cox NJ (1997) Allele-sharing models: LOD scores and accurate linkage tests. Am J Hum Genet 61:1179–1188 [DOI] [PMC free article] [PubMed]
- Kong A, Frigge M, Irwin M, Cox N (1992) Importance sampling. I. Computing multimodal P values in linkage analysis. Am J Hum Genet 51:1413–1429 [PMC free article] [PubMed]
- Kruglyak L, Daly MJ, Reeve-Daly MP, Lander ES (1996) Parametric and nonparametric linkage analysis: a unified multipoint approach. Am J Hum Genet 58:1347–1363 [PMC free article] [PubMed] [Google Scholar]
- Kruglyak L, Lander E (1995) Complete multipoint sib pair analysis of qualitative and quantitative traits. Am J Hum Genet 57:439–454 [PMC free article] [PubMed]
- Lathrop GM, Ott J (1990) Analysis of complex diseases under oligogenic models and intrafamilial heterogeneity by the LINKAGE programs. Am J Hum Genet Suppl 47:A188 [Google Scholar]
- Luo D-F, Bui MM, Muir A, Maclaren NK, Thomson G, She J-X (1995) Affected-sib-pair mapping of a novel susceptibility gene to insulin-dependent diabetes mellitus (IDDM8) on chromosome 6q25-q27. Am J Hum Genet 57:911–919 [PMC free article] [PubMed]
- Lynch M, Walsh B (1998) Genetics and analysis of quantitative traits. Sinauer Associates, Sunderland, MA [Google Scholar]
- Mein CA, Esposito L, Dunn MG, Johnson GCL, Timms AE, Goy JV, Smith AN, et al (1998) A search for type 1 diabetes susceptibility genes in families from the United Kingdom. Nature Genetics 19:297–300 [DOI] [PubMed]
- Meunier F, Philippi A, Martinez M, Demenais F (1997) Affected sib-pair tests for linkage: Type 1 errors with dependent sib-pairs. Genet Epidemiol 14:1107–1111 [DOI] [PubMed] [Google Scholar]
- Olson J (1997) Likelihood-based models for genetic linkage analysis using affected sib pairs. Hum Hered 47:110–120 [DOI] [PubMed]
- Reed P, Cucca F, Jenkins S, Merriman M, Wilson A, McKinney P, Bosi E, et al (1997) Evidence for a type 1 diabetes susceptibility locus (IDDM10) on human chromosome 10p11-q11. Hum Mol Genet 6:1011–1016 [DOI] [PubMed]
- Risch N (1990_a_) Linkage strategies for genetically complex traits. I. Multilocus models. Am J Hum Genet 46:222–228 [PMC free article] [PubMed]
- ——— (1990_b_) Linkage strategies for genetically complex traits. II. The power of affected relative pairs. Am J Hum Genet 46:229–241 [PMC free article] [PubMed]
- ——— (1990_c_) Linkage strategies for genetically complex traits. III. The effect of marker polymorphism on analysis of affected relative pairs. Am J Hum Genet 46:242–253 [PMC free article] [PubMed]
- S.A.G.E. (1998) Statistical analysis for genetic epidemiology, beta 4.0-1. Computer program package available from the Department of Epidemiology and Biostatistics, Rammelkamp Center for Education and Research, MetroHealth Campus, Case Western Reserve University, Cleveland [Google Scholar]
- Schork NJ, Boehnke M., Terwilliger JD, Ott J (1993) Two-trait-locus linkage analysis: a powerful strategy for mapping complex genetic traits. Am J Hum Genet 53:1127–1136 [PMC free article] [PubMed]
- Strauch K, Fimmers R, Baur MP (1998) Parametric and non-parametric multipoint linkage analysis for two-locus disease models. Genet Epidemiol 15:523 [Google Scholar]
- Tiwari HK, Elston RC (1997) Linkage of multilocus components of variance to polymorphic markers. Ann Hum Genet 61:253–261 [DOI] [PubMed]
- Trustrum GB (1961) The correlations between relatives in a random mating diploid population. Proc Cambridge Phil Soc 57:315–320 [Google Scholar]
- Weeks DE, Lange K (1988) The affected-pedigree-member method of linkage analysis. Am J Hum Genet 42:315–326 [PMC free article] [PubMed]
- Whittemore AS, Halpern J (1994) A class of tests of linkage using affected pedigree members. Biometrics 50:118–127 [PubMed]
- Xu J, The Collaborative Study on the Genetics of Asthma (1998) Search for statistical interactions in data from genome-wide screen for asthma susceptibility loci in three US populations. Genet Epidemiol 15:549 [Google Scholar]
- Zhao H, Merikengas KR, Kidd KK (1999) On a randomization procedure in linkage analysis. Am J Hum Genet 65:1449–1456 [DOI] [PMC free article] [PubMed]
- Zinn-Justin A, Abel L (1998) Two-locus developments of the weighted pairwise correlation method for linkage analysis. Genet Epidemiol 15:491–510 [DOI] [PubMed] [Google Scholar]